Abstract
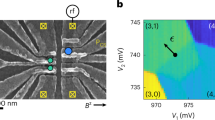
Silicon has many attractive properties for quantum computing, and the quantum-dot architecture is appealing because of its controllability and scalability. However, the multiple valleys in the silicon conduction band are potentially a serious source of decoherence for spin-based quantum-dot qubits. Only when a large energy splits these valleys do we obtain well-defined and long-lived spin states appropriate for quantum computing. Here, we show that the small valley splittings observed in previous experiments on Si–SiGe heterostructures result from atomic steps at the quantum-well interface. Lateral confinement in a quantum point contact limits the electron wavefunctions to several steps, and enhances the valley splitting substantially, up to 1.5 meV. The combination of electrostatic and magnetic confinement produces a valley splitting larger than the spin splitting, which is controllable over a wide range. These results improve the outlook for realizing spin qubits with long coherence times in silicon-based devices.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout





Similar content being viewed by others
References
Cirac, J. & Zoller, P. Quantum computations with cold trapped ions. Phys. Rev. Lett. 74, 4091–4094 (1995).
Loss, D. & DiVincenzo, D. P. Quantum computation with quantum dots. Phys. Rev. A 57, 120–126 (1998).
Ciorga, M. et al. Addition spectrum of a lateral dot from Coulomb and spin-blockade spectroscopy. Phys. Rev. B 61, R16315–R16318 (2000).
Fujisawa, T., Austing, D. G., Tokura, Y., Hirayama, Y. & Tarucha, S. Allowed and forbidden transitions in artificial hydrogen and helium atoms. Nature 419, 278–281 (2002).
Elzerman, J. M. et al. Single-shot read-out of an individual electron spin in a quantum dot. Nature 430, 431–435 (2004).
Johnson, A. C. et al. Tripletsinglet spin relaxation via nuclei in a double quantum dot. Nature 435, 925–928 (2005).
Petta, J. R. et al. Coherent manipulation of coupled electron spins in semiconductor quantum dots. Science 309, 2180–2184 (2005).
Shnirman, A., Schön, G. & Hermon, Z. Quantum manipulations of small Josephson junctions. Phys. Rev. Lett. 79, 2371–2374 (1997).
Nielsen, M. & Chuang, I. Quantum Computation and Quantum Information (Cambridge Univ. Press, Cambridge, 2000).
Cerletti, V., Coish, W. A., Gywat, O. & Loss, D. Recipes for spin-based quantum computing. Nanotechnology 16, R27–R49 (2005).
Kane, B. E. A silicon-based nuclear spin quantum computer. Nature 393, 133–137 (1998).
Yablonovitch, E. et al. Optoelectronic quantum telecommunications based on spins in semiconductors. Proc. IEEE 91, 761–780 (2003).
Schäffler, F. High-mobility Si and Ge structures. Semicond. Sci. Technol. 12, 1515–1549 (1997).
Ando, T., Fowler, A. B. & Stern, F. Electronic properties of two-dimensional systems. Rev. Mod. Phys. 54, 437–672 (1982).
Boykin, T. B. et al. Valley splitting in strained silicon quantum wells. Appl. Phys. Lett. 84, 115–117 (2004).
Weitz, P., Haug, R. J., von Klitzing, K. & Schäffler, F. Tilted magnetic field studies of spin- and valley-splittings in Si/Si1−xGex heterostructures. Surf. Sci. 361/362, 542–546 (1996).
Koester, S. J., Ismail, K. & Chu, J. O. Determination of spin- and valley-split energy levels in strained Si quantum wells. Semicond. Sci. Technol. 12, 384–388 (1997).
Khrapai, V. S., Shashkin, A. A. & Dolgopolov, V. P. Strong enhancement of the valley splitting in a two-dimensional electron system in silicon. Phys. Rev. B 67, 113305 (2003).
Lai, K. et al. Two-flux composite fermion series of the fractional quantum Hall states in strained Si. Phys. Rev. Lett. 93, 156805 (2004).
Pudalov, V. M., Punnoose, A., Brunthaler, G., Prinz, A. & Bauer, G. Valley splitting in Si-inversion layers at low magnetic fields. Preprint at <http://arxiv.org/abs/cond-mat/0104347> (2001).
Dobers, M., von Klitzing, K., Schneider, J., Weimann, G. & Ploog, K. Electrical detection of nuclear magnetic resonance in GaAs–AlxGa1−xAs heterostructures. Phys. Rev. Lett. 61, 1650–1653 (1988).
Ando, T. Valley splitting in the silicon inversion layer: Misorientation effects. Phys. Rev. B 19, 3089–3095 (1979).
Friesen, M., Eriksson, M. A. & Coppersmith, S. N. Magnetic field dependence of valley splitting in realistic Si/SiGe quantum wells. Appl. Phys. Lett. 89, 202106 (2006).
Kohn, W. in Solid State Physics Vol. 5 (eds Seitz, F. & Turnbull, D.) 257–319 (Academic, New York, 1957).
Koiller, B., Hu, X. & das Sarma, S. Exchange in silicon-based quantum computer architecture. Phys. Rev. Lett. 88, 027903 (2002).
Van Wees, B. J. et al. Quantized conductance of point contacts in a two-dimensional electron gas. Phys. Rev. Lett. 60, 848–850 (1988).
Van Wees, B. J. et al. Quantum ballistic and adiabatic electron transport studied with quantum point contacts. Phys. Rev. B 43, 12431–12453 (1991).
Ohkawa, F. J. & Uemura, Y. Theory of valley splitting in an N-channel (100) inversion layer of Si III. Enhancement of splittings by many-body effects. J. Phys. Soc. Jpn 43, 925–932 (1977).
Jiang, H. W. & Yablonovitch, E. Gate-controlled electron spin resonance in GaAs/AlxGa1−xAs heterostructures. Phys. Rev. B 64, 041307 (2001).
Takashina, K., Ono, Y., Fujiwara, A., Takahashi, Y. & Hirayama, Y. Valley polarization in Si(100) at zero magnetic field. Phys. Rev. Lett. 96, 236801 (2006).
Roberts, M. M. et al. Elastically relaxed free-standing strained-silicon nanomembranes. Nature Mater. 5, 388–393 (2006).
Ismail, K., Arafa, M., Saenger, K. L., Chu, J. O. & Meyerson, B. S. Extremely high electron mobility in Si/SiGe modulation-doped heterostructures. Appl. Phys. Lett. 66, 1077–1079 (1995).
Klein, L. J. et al. Coulomb blockade in a silicon/silicon-germanium two-dimensional electron gas quantum dot. Appl. Phys. Lett. 84, 4047–4049 (2004).
Cronenwett, S. M. et al. Low-temperature fate of the 0. 7 structure in a point contact: A Kondo-like correlated state in an open system. Phys. Rev. Lett. 88, 226805 (2002).
Acknowledgements
We gratefully acknowledge conversations with R. Blick. This work was supported by NSA/LPS under ARO contract number W911NF-04-1-0389, and by the National Science Foundation through the ITR programme (DMR-0325634) and the EMT programme (CCF-0523675).
Author information
Authors and Affiliations
Contributions
J.C. and P.M. provided the samples. S.G., K.S., L.M., J.T., and L.K. carried out the fabrication and measurements. M.F., C.T., R.J. and S.C. did the theoretical work. S.G., K.S., L.M., M.F., S.C. and M.E. analysed the data. M.F., R.J., D.W., S.C., M.F. and M.E. planned the project. M.F., K.S., S.C. and M.E. prepared the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Rights and permissions
About this article
Cite this article
Goswami, S., Slinker, K., Friesen, M. et al. Controllable valley splitting in silicon quantum devices. Nature Phys 3, 41–45 (2007). https://doi.org/10.1038/nphys475
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys475
This article is cited by
-
Impact of the valley orbit coupling on exchange gate for spin qubits in silicon
npj Quantum Information (2022)
-
Fast spin-valley-based quantum gates in Si with micromagnets
npj Quantum Information (2021)
-
Two-axis quantum control of a fast valley qubit in silicon
npj Quantum Information (2019)
-
Electrically driven electron spin resonance mediated by spin–valley–orbit coupling in a silicon quantum dot
npj Quantum Information (2018)
-
Spin decoherence in a two-qubit CPHASE gate: the critical role of tunneling noise
npj Quantum Information (2018)