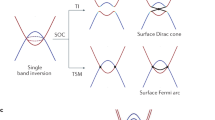
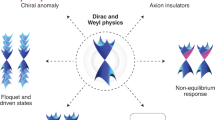
Abstract
The physical description of all materials is rooted in quantum mechanics, which describes how atoms bond and electrons interact at a fundamental level. Although these quantum effects can in many cases be approximated by a classical description at the macroscopic level, in recent years there has been growing interest in material systems where quantum effects remain manifest over a wider range of energy and length scales. Such quantum materials include superconductors, graphene, topological insulators, Weyl semimetals, quantum spin liquids, and spin ices. Many of them derive their properties from reduced dimensionality, in particular from confinement of electrons to two-dimensional sheets. Moreover, they tend to be materials in which electrons cannot be considered as independent particles but interact strongly and give rise to collective excitations known as quasiparticles. In all cases, however, quantum-mechanical effects fundamentally alter properties of the material. This Review surveys the electronic properties of quantum materials through the prism of the electron wavefunction, and examines how its entanglement and topology give rise to a rich variety of quantum states and phases; these are less classically describable than conventional ordered states also driven by quantum mechanics, such as ferromagnetism.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout





Similar content being viewed by others
References
Parkin, S. S. P. et al. Giant tunnelling magnetoresistance at room temperature with MgO (100) tunnel barriers. Nat. Mater. 3, 862–867 (2004).
Yuasa, S., Nagahama, T., Fukushima, A., Suzuki, Y. & Ando, K. Giant room-temperature magnetoresistance in single-crystal Fe/MgO/Fe magnetic tunnel junctions. Nat. Mater. 3, 868–871 (2004).
Yin, J. et al. Satellite-based entanglement distribution over 1200 kilometers. Science 356, 1140–1144 (2017).
Schrödinger, E. Discussion of probability relations between separated systems. Math. Proc. Cambr. 31, 555–563 (1935).
Shoenberg, D. Magnetic Oscillations in Metals (Cambridge Univ. Press, 1984).
Bardeen, J., Cooper, L. N. & Schrieffer, J. R. Theory of superconductivity. Phys. Rev. 108, 1175–1204 (1957).
Bednorz, J. G. & Müller, K. A. Possible high Tc superconductivity in the Ba–La–Cu–O system. Z. Phys. B 64, 189–193 (1986).
Drozdov, A. P., Eremets, M. I., Troyan, I. A., Ksenofontov, V. & Shylin, S. I. Conventional superconductivity at 203 kelvin at high pressures in the sulfur hydride system. Nature 525, 73–76 (2015).
Balasubramanian, G. et al. Ultralong spin coherence time in isotopically engineered diamond. Nat. Mater. 8, 383–387 (2009).
Maurer, P. C. et al. Room-temperature quantum bit memory exceeding one second. Science 336, 1283–1286 (2012).
Savary, L. & Balents, L. Quantum spin liquids: a review. Rep. Prog. Phys. 80, 016502 (2017). This paper provides a timely and accessible review of theoretical work on quantum spin liquids and the challenges facing materials research in this field.
A longer overview under the auspices of the US Department of Energy is “Basic Research Needs Workshop on Quantum Materials for Energy Relevant Technology”, Broholm, C., Fisher, I., Moore, J. & Murnane, M. (Office of Science, US Department of Energy, 2016); http://science.energy.gov/bes/efrc/research/bes-reports
Basov, D. N., Averitt, R. D. & Hsieh, D. Controlling the properties of quantum materials. Nat. Mater. 16, 1077–1088 (2017).
Tokura, Y., Kawasaki, M. & Nagaosa, N. Emergent functions of quantum materials. Nat. Phys. 13, 1056–1068 (2017).
James, H. M. & Coolidge, A. S. The ground state of the hydrogen molecule. J. Chem. Phys. 1, 825–835 (1933).
Blunt, N. S. et al. Semi-stochastic full configuration interaction quantum Monte Carlo: developments and application. J. Chem. Phys. 142, 184107 (2015).
Goodenough, J. B. Theory of the role of covalence in the perovskite-type manganites [La, M(II)]MnO3 . Phys. Rev. 100, 564–573 (1955).
Kanamori, J. Superexchange interaction and symmetry properties of electron orbitals. J. Phys. Chem. Solids 10, 87–98 (1959).
Franchini, C. et al. Maximally localized Wannier functions in LaMnO3 within PBE + U, hybrid functionals and partially self-consistent GW: an efficient route to construct ab initio tight-binding parameters for eg perovskites. J. Phys. Condens. Matter 24, 235602 (2012).
Marques, M. A. L. et al. Ab initio theory of superconductivity. II. Application to elemental metals. Phys. Rev. B 72, 024546 (2005).
Giustino, F. Electron–phonon interactions from first principles. Rev. Mod. Phys. 89, 015003 (2017).
Jackeli, G. & Khaliullin, G. Mott insulators in the strong spin–orbit coupling limit: from Heisenberg to a quantum compass and Kitaev models. Phys. Rev. Lett. 102, 017205 (2009). This theoretical work showed how bond-directional exchange interactions and Kitaev models can be realized in magnetic insulators with strong spin–orbit coupling.
Plumb, K. W. et al. α-RuCl3: a spin–orbit assisted Mott insulator on a honeycomb lattice. Phys. Rev. B 90, 041112(R) (2014).
Takayama, T. et al. Hyperhoneycomb iridate β-Li2IrO3 as a platform for Kitaev magnetism. Phys. Rev. Lett. 114, 077202 (2015).
Chun, S. H. et al. Direct evidence for dominant bond-directional interactions in a honeycomb lattice iridate Na2IrO3 . Nat. Phys. 11, 462–466 (2015).
Rüegg, Ch. et al. Pressure-induced quantum phase transition in the spin-liquid TlCuCl3 . Phys. Rev. Lett. 93, 257201 (2004). These authors established a model system that allows detailed, quantitative neutron scattering experiments on the evolution of spin correlations across a quantum phase transition.
Jain, A. et al. Higgs mode and its decay in a two-dimensional antiferromagnet. Nat. Phys. 13, 633–637 (2017).
Hong, T. et al. Higgs amplitude mode in a two-dimensional quantum antiferromagnet near the quantum critical point. Nat. Phys. 13, 638–643 (2017).
Pekker, D. & Varma, C. M. Amplitude/Higgs modes in condensed matter physics. Annu. Rev. Condens. Matter Phys. 6, 269–297 (2014).
Cercellier, H. et al. Evidence for an excitonic insulator phase in 1T-TiSe2 . Phys. Rev. Lett. 99, 146403 (2007). The photoemission data presented in this paper revived interest in excitonic insulators. The data were taken on a material system that is now being studied intensely in the form of exfoliated monolayers.
Wakisaka, Y. et al. Excitonic insulator state in Ta2NiSe5 probed by photoemission spectroscopy. Phys. Rev. Lett. 103, 026402 (2009).
Lu, Y. F. et al. Zero-gap semiconductor to excitonic insulator transition in Ta2NiSe5 . Nat. Commun. 8, 14408 (2017).
Jérome, D., Rice, T. M. & Kohn, W. Excitonic insulator. Phys. Rev. 158, 462–475 (1967).
Morosan, E. et al. Superconductivity in CuxTiSe2 . Nat. Phys. 2, 544–550 (2006).
Kusmartseva, A. F., Sipos, B., Berger, H., Forró, L. & Tutiš, E. Pressure induced superconductivity in pristine 1T-TiSe2 . Phys. Rev. Lett. 103, 236401 (2009).
Joe, Y. I. et al. Emergence of charge density wave domain walls above the superconducting dome in 1T-TiSe2 . Nat. Phys. 10, 421–425 (2014).
Edge, J. M., Kedem, Y., Aschauer, U., Spaldin, N. A. & Balatsky, A. V. Quantum critical origin of the superconducting dome in SrTiO3 . Phys. Rev. Lett. 115, 247002 (2016).
Ruhman, J. & Lee, P. A. Superconductivity at very low density: the case of strontium titanate. Phys. Rev. B 94, 224515 (2016).
Ohtomo, A. & Hwang, H. Y. A high-mobility electron gas at the LaAlO3/SrTiO3 heterointerface. Nature 427, 423–426 (2004). A variety of quantum states have now been observed to emerge at atomic-scale interfaces between correlated materials. The creation of such interfaces was enabled by progress in materials synthesis highlighted in this paper.
Boschker, H. & Mannhart, J. Quantum-matter heterostructures. Annu. Rev. Condens. Matter Phys. 8, 145–164 (2017).
Novoselov, K. S., Mishchenko, A., Carvalho, A. & Castro Neto, A. H. 2D materials and van der Waals heterostructures. Science 353, aac9439 (2016).
Kamihara, Y. et al. Iron-based layered superconductor: LaOFeP. J. Am. Chem. Soc. 128, 10012–10013 (2006).
Hsu, F. C. et al. Superconductivity in the PbO-type structure α-FeSe. Proc. Natl Acad. Sci. USA 105, 14262–14264 (2008).
Si, Q., Yu, R. & Abrahams, E. High-temperature superconductivity in iron pnictides and chalcogenides. Nat. Rev. Mater. 1, 16017 (2016).
Dai, P. C. Antiferromagnetic order and spin dynamics in iron-based superconductors. Rev. Mod. Phys. 87, 855–896 (2015).
Wang, F., Zhai, H., Ran, Y., Vishwanath, A. & Lee, D.-H. Functional renormalization-group study of the pairing symmetry and pairing mechanism of the FeAs-based high-temperature superconductor. Phys. Rev. Lett. 102, 047005 (2009). The functional renormalization group approach gives a way to understand how various electron–electron interactions and Fermi surfaces combine to lead to the different superconducting ordering parameters observed in iron-based superconductors.
Metzner, W., Salmhofer, M., Honerkamp, C., Meden, V. & Schönhammer, K. Functional renormalization group approach to correlated fermion systems. Rev. Mod. Phys. 84, 299–352 (2012).
Imada, M., Fujimori, A. & Tokura, Y. Metal–insulator transitions. Rev. Mod. Phys. 70, 1039–1263 (1998).
LeBlanc, J. P. F. et al. Solutions of the two-dimensional Hubbard model: benchmarks and results from a wide range of numerical algorithms. Phys. Rev. X 5, 041041 (2015).
Fradkin, E., Kivelson, S. A. & Tranquada, J. M. Theory of intertwined orders in high temperature superconductors. Rev. Mod. Phys. 87, 457–482 (2015). This paper provides a lively yet in-depth review of current research on intertwined order and electronic analogues of liquid crystals in copper oxide superconductors.
Tranquada, J. M. et al. Evidence for unusual superconducting correlations coexisting with stripe order in La1.875Ba0.125CuO4 . Phys. Rev. B 78, 174529 (2008).
Dagotto, E. Complexity in strongly correlated electronic systems. Science 309, 257–262 (2005).
Keimer, B., Kivelson, S. A., Norman, M. R., Uchida, S. & Zaanen, J. From quantum matter to high-temperature superconductivity in copper oxides. Nature 518, 179–186 (2015).
Stewart, G. R. Unconventional superconductivity. Adv. Phys. 6, 75–196 (2017).
Scalapino, D. J. A common thread: the pairing interaction for unconventional superconductors. Rev. Mod. Phys. 84, 1383–1417 (2012).
Sachdev, S. & Keimer, B. Quantum criticality. Phys. Today 64, 29–35 (February, 2011).
Sebastian, S. E. & Proust, C. Quantum oscillations in hole-doped cuprates. Annu. Rev. Condens. Matter Phys. 6, 411–430 (2015).
Sebastian, S. E. et al. Normal-state nodal electronic structure in underdoped high-Tc copper oxides. Nature 511, 61–64 (2014).
Ramshaw, B. J. et al. Quasiparticle mass enhancement approaching optimal doping in a high-Tc superconductor. Science 348, 317–320 (2015).
Braicovich, L. et al. Dispersion of magnetic excitations in the cuprate La2CuO4 and CaCuO2 compounds measured using resonant X-ray scattering. Phys. Rev. Lett. 102, 167401 (2009). This paper introduced resonant inelastic X-ray scattering (RIXS) as an energy- and momentum-resolved probe of collective spin excitations in metal oxides. The sensitivity of RIXS now allows detection of dispersive magnons in thin films and at interfaces.
Hu, W. et al. Optically enhanced coherent transport in YBa2Cu3O6.5 by ultrafast redistribution of interlayer coupling. Nat. Mater. 13, 705–711 (2014).
Carrasquilla, J. & Melko, R. G. Machine learning phases of matter. Nat. Phys. 13, 431–434 (2017).
Booth, G. H., Grüneis, A., Kresse, G. & Alavi, A. Towards an exact description of electronic wavefunctions in real solids. Nature 493, 365–370 (2013).
Schneider, U. et al. Fermionic transport and out-of-equilibrium dynamics in a homogeneous Hubbard model with ultracold atoms. Nat. Phys. 8, 213–218 (2012).
Cheuk, L. W. et al. Observation of spatial charge and spin correlations in the 2D Fermi–Hubbard model. Science 353, 1260–1264 (2016).
Norman, M. R. Materials design for new superconductors. Rep. Prog. Phys. 79, 074502 (2016).
von Klitzing, K., Dorda, G. & Pepper, M. New method for high-accuracy determination of the fine-structure constant based on quantized Hall resistance. Phys. Rev. Lett. 45, 494–497 (1980).
Thouless, D. J., Kohmoto, M., Nightingale, M. P. & den Nijs, M. Quantized Hall conductance in a two-dimensional periodic potential. Phys. Rev. Lett. 49, 405–408 (1982). The importance of this classic paper on how topology of wavefunctions (specifically, the Berry phase of Bloch electrons) underlies the integer quantum Hall effect only became fully clear two decades later.
Haldane, F. D. M. Model for a quantum Hall effect without Landau levels: condensed-matter realization of the ‘parity anomaly’. Phys. Rev. Lett. 61, 2015–2018 (1988).
Murakami, S., Nagaosa, N. & Zhang, S.-C. Spin-Hall insulator. Phys. Rev. Lett. 93, 156804 (2004).
Kane, C. L. & Mele, E. J. Z2 topological order and the quantum spin Hall effect. Phys. Rev. Lett. 95, 146802 (2005). The possibility of a new type of topological invariant enabled by time-reversal symmetry in systems with spin–orbit coupling was spelled out clearly in this paper on two-dimensional electron systems, which inspired a great deal of subsequent theoretical work.
König, M. et al. Quantum spin Hall insulator state in HgTe quantum wells. Science 318, 766–770 (2007).
Bernevig, B. A., Hughes, T. L. & Zhang, S.-C. Quantum spin Hall effect and topological phase transition in HgTe quantum wells. Science 314, 1757–1761 (2006).
Moore, J. E. & Balents, L. Topological invariants of time-reversal-invariant band structures. Phys. Rev. B 75, 121306(R) (2007).
Fu, L., Kane, C. L. & Mele, E. J. Topological insulators in three dimensions. Phys. Rev. Lett. 98, 106803 (2007).
Roy, R. Topological phases and the quantum spin Hall effect in three dimensions. Phys. Rev. B 79, 195322 (2009).
Xia, Y. et al. Observation of a large-gap topological-insulator class with a single Dirac cone on the surface. Nat. Phys. 5, 398–402 (2009). Previous topological states were discovered primarily by transport measurements. Many of the discoveries in the last ten years were enabled by angle-resolved photoemission, as in this work, which found the Dirac cone electronic structure at the surface of bismuth selenide.
Zhang, H. et al. Topological insulators in Bi2Se3, Bi2Te3 and Sb2Te3 with a single Dirac cone on the surface. Nat. Phys. 5, 438–442 (2009).
Qi, X.-L., Hughes, T. L. & Zhang, S.-C. Topological field theory of time-reversal invariant insulators. Phys. Rev. B 78, 195424 (2008). This paper gave a more abstract/emergent picture of what topological insulators are, by making a profound connection between topological insulators and previous work on possible electromagnetic responses in solids (‘axion electrodynamics’).
Essin, A. M., Moore, J. E. & Vanderbilt, D. Magnetoelectric polarizability and axion electrodynamics in crystalline insulators. Phys. Rev. Lett. 102, 146805 (2009).
Wu, L. et al. Quantized Faraday and Kerr rotation and axion electrodynamics of a 3D topological insulator. Science 354, 1124–1127 (2016).
Chang, C. Z. et al. Experimental observation of the quantum anomalous Hall effect in a magnetic topological insulator. Science 340, 167–170 (2013).
Liu, Z. K. et al. A stable three-dimensional topological Dirac semimetal Cd3As2 . Nat. Mater. 13, 677–681 (2014).
Neupane, M. et al. Observation of a topological 3D Dirac semimetal phase in high-mobility Cd3As2 . Nat. Commun. 5, 3786 (2014).
Borisenko, S. et al. Experimental realization of a three-dimensional Dirac semimetal. Phys. Rev. Lett. 113, 027603 (2014).
Murakami, S. Phase transition between the quantum spin Hall and insulator phases in 3D: emergence of a topological gapless phase. New J. Phys. 9, 356 (2007).
Burkov, A. A. & Balents, L. Weyl semimetal in a topological insulator multilayer. Phys. Rev. Lett. 107, 127205 (2011).
Nielsen, H. B. & Ninomiya, M. A no-go theorem for regularizing chiral fermions. Phys. Lett. B 105, 219–223 (1981).
Wan, X., Turner, A. M., Vishwanath, A. & Savrasov, S. Y. Topological semimetal and Fermi-arc surface states in the electronic structure of pyrochlore iridates. Phys. Rev. B 83, 205101 (2011).
Vafek, O. & Vishwanath, A. Dirac fermions in solids: from high-Tc cuprates and graphene to topological insulators and Weyl semimetals. Annu. Rev. Condens. Matter Phys. 5, 83–112 (2014).
Son, D. T. & Spivak, B. Z. Chiral anomaly and classical negative magnetoresistance of Weyl metals. Phys. Rev. B 88, 104412 (2013).
Xiong, J. et al. Evidence for the chiral anomaly in the Dirac semimetal Na3Bi. Science 350, 413–416 (2015).
Huang, S.-M. et al. Weyl Fermion semimetal with surface Fermi arcs in the transition metal monopnictide TaAs class. Nat. Commun. 6, 7373 (2015).
Weng, H., Fang, C., Fang, Z., Bernevig, A. & Dai, X. Weyl semimetal phase in non-centrosymmetric transition metal monophosphides. Phys. Rev. X 5, 011029 (2015).
Xu, S.-Y. et al. Discovery of a Weyl Fermion semimetal and topological Fermi arcs. Science 349, 613–617 (2015).
Cho, G. Y., Bardarson, J. H., Lu, Y. M. & Moore, J. E. Superconductivity of doped Weyl semimetals: finite-momentum pairing and electronic analog of the 3He-A phase. Phys. Rev. B 86, 214514 (2012).
Dzero, M., Xia, J., Galitski, V. & Coleman, P. Topological Kondo insulators. Annu. Rev. Condens. Matter Phys. 7, 249–280 (2016).
Ando, Y. & Fu, L. Topological crystalline insulators and topological superconductors: from concepts to materials. Annu. Rev. Condens. Matter Phys. 6, 361–381 (2015).
Tsui, D. C., Stormer, H. L. & Gossard, A. C. Two-dimensional magnetotransport in the extreme quantum limit. Phys. Rev. Lett. 48, 1559–1562 (1982).
Laughlin, R. B. Anomalous quantum Hall effect: an incompressible quantum fluid with fractionally charged excitations. Phys. Rev. Lett. 50, 1395–1398 (1983).
Leinaas, J. M. & Myrheim, J. On the theory of identical particles. Nuovo Cimento B 37, 1–23 (1977).
Willett, R. et al. Observation of an even-denominator quantum number in the fractional quantum Hall effect. Phys. Rev. Lett. 59, 1776–1779 (1987).
Moore, G. & Read, N. Non-Abelions in the fractional quantum Hall effect. Nucl. Phys. B 360, 362–396 (1991).
Nayak, C., Simon, S. H., Stern, A., Freedman, M. & Sarma, S. D. Non-Abelian anyons and topological quantum computation. Rev. Mod. Phys. 80, 1083–1159 (2008).
Read, N. & Green, D. Paired states of fermions in two dimensions with breaking of parity and time-reversal symmetries, and the fractional quantum Hall effect. Phys. Rev. B 61, 10267–10297 (2000). This paper greatly clarified the relationship between the seemingly different problems of superconductivity and exotic non-Abelian fractional quantum Hall phases. It turns out that even a simple superconducting wavefunction of BCS type contains within it non-Abelian order.
Maeno, Y., Kittaka, S., Nomura, T., Yonezawa, S. & Ishida, K. Evaluation of spin-triplet superconductivity in Sr2RuO4 . J. Phys. Soc. Jpn 81, 011009 (2012).
Mourik, V. et al. Signatures of Majorana fermions in hybrid superconductor–semiconductor nanowire devices. Science 336, 1003–1007 (2012).
Nadj-Perge, S. et al. Observation of Majorana fermions in ferromagnetic atomic chains on a superconductor. Science 346, 602–607 (2014).
Albrecht, S. M. et al. Exponential protection of zero modes in Majorana islands. Nature 531, 206–209 (2016).
Volovik, G. E. The Universe in a Helium Droplet (International Series of Monographs on Physics, Oxford Univ. Press, 2009).
Moessner, R. & Sondhi, S. Resonating valence bond phase in the triangular lattice quantum dimer model. Phys. Rev. Lett. 86, 1881–1884 (2001).
Han, T. H. et al. Fractionalized excitations in the spin-liquid state of a kagome-lattice antiferromagnet. Nature 492, 406–410 (2012).
Kitaev, A. Anyons in an exactly solved model and beyond. Ann. Phys. 321, 2–111 (2006).
Banerjee, A. et al. Proximate Kitaev quantum spin liquid behaviour in a honeycomb magnet. Nat. Mater. 15, 733–740 (2016).
Lee, P. A., Nagaosa, N. & Wen, X.-G. Doping a Mott insulator: physics of high-temperature superconductivity. Rev. Mod. Phys. 78, 17–85 (2006).
Sachdev, S. Emergent gauge fields and the high temperature superconductors. Phil. Trans. R. Soc. A 374, 20150248 (2016).
Senthil, T., Vishwanath, A., Balents, L., Sachdev, S. & Fisher, M. P. A. Deconfined quantum critical points. Science 303, 1490–1494 (2004).
Hwang, H. Y. et al. Emergent phenomena at oxide interfaces. Nat. Mater. 11, 103–113 (2012).
Hoffmann, A. & Bader, S. D. Opportunities at the frontiers of spintronics. Phys. Rev. Appl. 4, 047001 (2015).
Bozhko, D. A. et al. Supercurrent in a room-temperature Bose–Einstein magnon condensate. Nat. Phys. 12, 1057–1062 (2016).
Schulz, T. et al. Emergent electrodynamics of skyrmions in a chiral magnet. Nat. Phys. 8, 301–304 (2012). The experimental discovery of emergent magnetic skyrmion phases in MnSi and other materials led to an outpouring of experiment and theory, with significant potential for new kinds of magnetic storage and spintronic devices.
Acknowledgements
B.K. acknowledges financial support by the European Research Council under Advanced Grant No. 669550 (Com4Com) and by the German Science Foundation (DFG) in the Collaborative Research Center TRR80. J.E.M. was supported by the Office of Basic Energy Sciences, Materials Sciences and Engineering Division, of the US Department of Energy under Contract No. DE-AC02-05CH11231, and the National Science Foundation under grant DMR-1507141.
Author information
Authors and Affiliations
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
About this article
Cite this article
Keimer, B., Moore, J. The physics of quantum materials. Nature Phys 13, 1045–1055 (2017). https://doi.org/10.1038/nphys4302
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys4302
This article is cited by
-
Correlated order at the tipping point in the kagome metal CsV3Sb5
Nature Physics (2024)
-
Conventional and Unconventional Photon Blockade in a Double-Cavity Optomechanical System
Brazilian Journal of Physics (2024)
-
Orbital design of Berry curvature: pinch points and giant dipoles induced by crystal fields
npj Quantum Materials (2023)
-
Tunable topologically driven Fermi arc van Hove singularities
Nature Physics (2023)
-
Witnessing light-driven entanglement using time-resolved resonant inelastic X-ray scattering
Nature Communications (2023)