Instability in dynamic fracture and the failure of the classical theory of cracks

Abstract

Cracks, the major vehicle for material failure¹, undergo a micro-branching instability at ∼40% of their sonic limiting velocity in three dimensions^2,3,4,5,6. Recent experiments showed that in thin systems cracks accelerate to nearly their limiting velocity without micro-branching, until undergoing an oscillatory instability^7,8. Despite their fundamental importance, these dynamic instabilities are not explained by the classical theory of cracks¹, which is based on linear elasticity and an extraneous local symmetry criterion to predict crack paths⁹. We develop a two-dimensional theory for predicting arbitrary paths of ultrahigh-speed cracks, which incorporates elastic nonlinearity without extraneous criteria. We show that cracks undergo an oscillatory instability controlled by small-scale, near crack-tip, elastic nonlinearity. This instability occurs above an ultrahigh critical velocity and features an intrinsic wavelength proportional to the ratio of the fracture energy to the elastic modulus, in quantitative agreement with experiments. This ratio emerges as a fundamental scaling length assumed to play no role in the classical theory of cracks, but shown here to strongly influence crack dynamics.

Main

Crack propagation is the main mode of materials failure. It has been a topic of intense research for decades because of its enormous practical importance and fundamental theoretical interest. Despite considerable progress to date^{10,11,12,13,14,15}, the classical theory of brittle crack propagation¹ still falls short of explaining the rich dynamical behaviour of high-speed cracks in brittle solids such as glass, ceramics and other engineering, geological and biological materials that break abruptly and catastrophically.

This theory, termed linear elastic fracture mechanics (LEFM)¹, assumes that linear elastodynamics—a continuum version of Newton’s second law together with a linear relation between stress (force) and strain (deformation)—applies everywhere inside a stressed material except for a negligibly small region near the crack tip. It predicts the instantaneous crack velocity v by equating the elastic energy release rate G, controlled by the intensity of the stress divergence near the crack tip, with the fracture energy Γ(v). The scalar equation G = Γ(v) must be supplemented with an extraneous criterion to select the crack path; the most widely used one is the principle of local symmetry⁹, which assumes that cracks propagating along arbitrary paths feature a symmetric stress distribution near their tips.

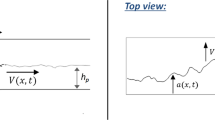
A central prediction of this theory is that straight cracks smoothly accelerate to the Rayleigh wave speed c_R (the velocity of surface acoustic waves) in large enough systems¹. However, cracks universally undergo symmetry-breaking instabilities before reaching their theoretical limiting velocity^2,3,4,5,6,7. In three-dimensional (3D) systems such as thick plates, instability is manifested by short-lived micro-cracks that branch out sideways from the main crack. This so-called micro-branching instability^2,3,4,5,6 typically occurs when v exceeds a threshold v_c of about 40% of c_R. Recent experiments in brittle gels have further shown that on reducing the thickness of the system, micro-branching is suppressed and instability is manifested at a much higher speed (v_c ∼ 90% of the shear wave speed c_s) by oscillatory cracks with a well-defined intrinsic wavelength λ (refs 7,8,15). Such behaviour cannot be explained by LEFM, even qualitatively, as it contains no length scales other than the external dimensions of the system.

To investigate dynamic fracture instabilities, we use the phase-field approach^{16,17,18,19,20}. By making the near-tip degradation zone spatially diffuse, this approach avoids the difficulty of tracking the evolution of sharp fracture surfaces inherent in traditional cohesive zone models¹. It is therefore capable of describing complex crack paths while treating both short-scale material failure and large-scale elasticity, without adopting the common assumption that elasticity remains linear at arbitrary large strains near the crack tip (Fig. 1a). This generalized approach features two intrinsic length scales missing in LEFM (Fig. 1b): the size ξ of the microscopic dissipation zone around the tip, where elastic energy is dissipated while creating new fracture surfaces, and the size ℓ of the near-tip nonlinear zone, where linear elasticity breaks down when strains become large. We stress that while ξ and ℓ are missing in LEFM, they are consistent with it as they remain much smaller than the system size. Moreover, ℓ scales with the ratio Γ/μ of the fracture energy to the shear modulus, but is generally much larger than Γ/μ and also depends on crack velocity. Experiments and theory suggest that this nonlinear scale may be related to the oscillatory instability^{8,15,21,22,23,24,25}, but this relationship is not fundamentally established. Here we develop a new phase-field formulation (see Methods and Supplementary Information) that maintains the wave speeds constant inside the dissipation zone, thereby avoiding spurious tip-splitting occurring in previous phase-field models at relatively low crack velocities²⁶. This new formulation allows us to model for the first time the ultrahigh-speed cracks observed experimentally.

Figure 1: Nonlinear elasticity and crack-tip length scales.

a, The stress σ, normalized by the shear modulus μ, versus strain ɛ for a linear elastic solid (blue line) and a nonlinear elastic solid (red line corresponding to e_strain defined by equation (4)) under uniaxial tension. Nonlinearity becomes important around ɛ_c ≈ 0.1. b, A schematic representation of near-tip length scales neglected in linear elastic fracture mechanics (LEFM), but consistent with it as long as they are much smaller than the system size. These include the dissipation zone of size ∼ξ, where elastic energy is dissipated in the process of creating new crack surfaces, and the nonlinear zone of size ∼ ℓ > ξ, where linearity breaks down. The region where linear elasticity breaks down, termed the ‘process zone’ in fracture mechanics, includes both the dissipation and nonlinear zones. To estimate ℓ, note first that the LEFM stress divergence , where r is the distance from the crack tip and K_I is the mode-I stress intensity factor, is valid for r close to, but larger than, ℓ. As ℓ is the region where elastic nonlinearity becomes important, it can be estimated by setting r ∼ ℓ and ɛ ∼ ɛ_c in the last expression. Finally, invoking energy balance in the tip region¹, Γ₀ ∝ K_I²/μ, one obtains ℓ ∼ ℓ₀/ɛ_c² ≫ ℓ₀, with ℓ₀ ≡ Γ₀/μ. Note that the velocity dependence of the fracture energy and the relativistic distortion of near-tip fields for crack velocities approaching c_s can both have a strong influence on the size and shape of this nonlinear region, going beyond this simple estimate.

The nonlinear strain energy density e_strain is chosen to correspond to an incompressible neo-Hookean solid (see Supplementary Information) (Fig. 1a), representing generic elastic nonlinearities and quantitatively describing the experiments of refs 6,7,8,15,21,25. We consider mode-I (tensile) cracks in strips of height H (in the y-direction) and length W (in the x-direction). Fixed tensile displacements u_y(y = ±H/2) = ±δ_y are imposed at the top and bottom boundaries with δ_y ≪ H such that strains are small and linear elasticity is valid everywhere in the sample except within a small region of size ℓ ≪ H near the crack tip, where elastic nonlinearity is important. The applied load is quantified by the stored elastic energy per unit length along x in the pre-stretched intact strip, G₀ = e_strainH, where e_strain is uniquely determined by δ_y.

Figure 2 unprecedentedly demonstrates the existence of a rapid crack oscillatory instability in our simulations. Figure 2a shows a close up on the crack at the onset of oscillations in the material (undeformed) coordinates (see also Supplementary Fig. 1 and Supplementary Movie 1) and a corresponding sequence of crack snapshots in the spatial (deformed) coordinates, along with the strain energy density field. The results bear striking resemblance to the corresponding experimental observations in brittle gels⁷, reproduced here in Fig. 2b (see also Supplementary Movie 2). Figure 2c shows the time evolution of the Cartesian components, (v_x, v_y), and magnitude of the crack velocity, , demonstrating that the instability appears when v exceeds a threshold v_c ≈0.92c_s. Figure 2d shows the time evolution of the oscillation amplitude A and wavelength λ, which both grow before saturating. The saturated amplitude is an order of magnitude smaller than the wavelength, in good agreement with experiments⁷.

Figure 2: Onset of the oscillatory instability.

Results of phase-field simulations of brittle mode-I (tensile) fracture in rectangular strips of height H and length W illustrating the onset of the oscillatory instability (full scale is available in Supplementary Fig. 1). a, Zoom in on the crack trajectory, defined by the φ = 1/2 contour, in the material (undeformed) frame (top) and a sequence of snapshots of the crack surfaces, along with the normalized strain energy density field e_strain/μ, in the spatial (deformed) frame (bottom). b, The corresponding experimental observations in brittle gels. c, The magnitude v, and the Cartesian components v_x and v_y, of the crack velocity (scaled by the shear wave speed c_s) versus crack propagation distance d (scaled by H). The onset of instability is marked by the dashed lines. d, The oscillation amplitude A and wavelength λ (scaled by ℓ₀ = Γ₀/μ) versus d/H. Simulation parameters are ℓ₀/ξ = 0.29, H/ξ = 300, W/ξ = 900, G₀/Γ₀ = 2.6 (corresponding to a background strain ɛ_yy = 3.62%), Δ = 0.21ξ and β = 0.28 (see Methods). Panel b adapted from ref. 7, APS.

Importantly, we verified that the wavelength is determined by an intrinsic length scale by carrying out simulations for different system sizes, yielding negligible variations in λ (Supplementary Fig. 2). Moreover, we verified that the instability is caused by near-tip elastic nonlinearity by repeating the simulations using the small-strain (linear elastic) quadratic approximation of the nonlinear e_strain, corresponding to conventional LEFM. These simulations yielded straight cracks that tip-split on surpassing a velocity of ≈0.9c_s, without oscillations. Since both forms of e_strain—nonlinear neo-Hookean and its small-strain linear elastic approximation—are nearly identical everywhere in the system outside the near-tip nonlinear zone, we conclude that nonlinearity within this zone is at the heart of the oscillatory instability.

To investigate the dependence of the oscillatory instability on the external load and material properties, we varied G₀/Γ₀, where Γ₀ ≡ Γ(v = 0) is the fracture energy at onset of crack propagation, and the material-dependent ratio Γ₀/(μξ) ≡ ℓ₀/ξ controls the relative strength of near-tip elastic nonlinearity and dissipation. Results of extensive simulations are shown in Fig. 3, presenting the crack velocity versus propagation distance for several G₀/Γ₀ values, and ℓ₀/ξ = 0.29 in Fig. 3a (also used in Fig. 2) and ℓ₀/ξ = 1.45 in Fig. 3b. The plots clearly show that the onset of instability occurs when v exceeds a threshold value v_c independently of the external load. Decreasing the load simply reduces the crack acceleration and hence v exceeds v_c after a larger propagation distance; instability is not observed for the lowest loads in Fig. 3a, b because v has not yet reached v_c by the end of the simulations. Comparing Fig. 3a and Fig. 3b, v_c is seen to increase by only a few per cent when Γ₀/(μξ) is increased fivefold. This result is consistent with the experimental finding that v_c remains nearly constant when the ratio of the fracture energy to the shear modulus is varied several fold by altering the composition of the brittle gels, which affects both quantities and hence their ratio⁷. Furthermore, the onset velocity v_c ≈ 0.92c_s in Figs 2 and 3a is in remarkably good quantitative agreement with experiments⁷.

Figure 3: Critical velocity of instability.

Results demonstrating the independence of the critical velocity of instability v_c on the external loading and the ratio of fracture energy to the shear modulus, which controls the size of the near-tip nonlinear zone. a,b, The normalized crack velocity v/c_s versus the normalized crack propagation distance d/H for different external loads, measured by the dimensionless ratio G₀/Γ₀, and ℓ₀/ξ = 0.29 (a) and ℓ₀/ξ = 1.45 (b). The critical velocity in b exceeds slightly c_R = 0.933 c_s due to elastic nonlinearity (see Supplementary Information). Other simulation parameters are H/ξ = 300, W/ξ = 300 (calculations with W/ξ = 900 yielded the same critical velocity v_c), Δ = 0.21ξ and β = 0.28.

Unlike the critical velocity of instability v_c, the wavelength of oscillations λ has been experimentally observed to significantly vary when the fracture energy Γ(v_c) and the shear modulus μ were changed by varying the material composition⁸. The phase-field framework allows one to independently vary Γ(v_c) and μ, and also to assess the role of the energy dissipation scale ξ. The size of the nonlinear zone ℓ is theoretically expected to be proportional to (and much larger than) Γ(v_c)/μ, but as the pre-factor is not sharply defined, we plot in Fig. 4a λ versus Γ(v_c)/μ, both scaled by ξ, where Γ(v_c)/μ ≈ 1.2Γ₀/μ is obtained from accelerating crack simulations (see Methods). We superimpose in Fig. 4a experimental measurements in brittle gels, where a value ξ ≃ 153 μm was chosen to match the y-intercepts of linear best fits of both the theoretical and experimental results. The slopes dλ/d(Γ(v_c)/μ), which are independent of the choice of ξ, are in remarkably good quantitative agreement. This agreement demonstrates that small-scale elastic nonlinearity, which is quantitatively captured by the phase-field approach, is a major determinant of the oscillation wavelength λ that increases linearly with Γ(v_c)/μ, when Γ(v_c)/(μξ) is sufficiently large. The existence of finite y-intercepts further suggests that the dynamics on the dissipation scale also affects λ. However, it should be emphasized that oscillations exist only above a minimum value of Γ(v_c)/(μξ) ∼ ℓ₀/ξ ≪ 1 (indistinguishable from the origin on the scale of Fig. 4a). This minimum reflects the fact that nonlinear effects become negligible when ℓ < ξ (or ℓ₀ ≪ ξ, since ℓ ≫ ℓ₀, see Fig. 1). Below this minimum, we observe the same behaviour as for linear elasticity: stable straight crack propagation and then tip-splitting with increasing load G₀/Γ₀. Above this minimum, oscillations with a wavelength following the linear fit in Fig. 4a exist over a finite range of loads that increases with increasing Γ(v_c)/(μξ). All in all, these results demonstrate the failure of the classical theory of fracture, which assumes that elastic nonlinearity plays no role. The singular role of elastic nonlinearity is further highlighted by our finding that the incorporation of Kelvin–Voigt viscosity¹⁷ in the linear elastic phase-field model does not suffice to produce an oscillatory instability. This result suggests that reversible nonlinear elastic deformation, as opposed to irreversible viscoelastic or viscoplastic dissipative processes, provides a general mechanism to destabilize high-speed cracks in conditions where nonlinear effects remain important outside the dissipation zone.

Figure 4: Critical wavelength of instability and crack-tip dynamics.

Results demonstrating a strong dependence of the wavelength of instability λ on the ratio of the fracture energy Γ(v_c) to the shear modulus μ, which controls the size of the near-tip nonlinear zone. a, The wavelength λ versus Γ(v_c)/μ (both quantities scaled by ξ). Experimental measurements in brittle gels (data taken from ref. 8) are superimposed on this plot by setting ξ ≃ 153 μm such that the y-intercepts of the best linear fits (dashed lines) of the theoretical and experimental results coincide. This ξ value is roughly consistent with experimental estimates⁸. Note that the theoretical data span a wider range of values compared with the experimental data, and do so in a much more continuous manner. The reason for this is that in the experiments Γ(v_c), μ and ξ are varied in a correlated (and not well-controlled) manner through varying the material composition, while in the theory these physical quantities can be varied independently so as to represent a broad range of different materials. b, The normalized crack-tip nonlinear deviation δ/ℓ₀ from the parabolic LEFM tip (see inset for a visual definition) versus the normalized crack velocity v/c_s. Inset, a snapshot of the crack surfaces and normalized strain energy density e_strain/μ in the spatial (deformed) coordinates for v/c_s = 0.93 (marked by the black square in the main panel). c, A sequence of snapshots of the crack surfaces and the normalized strain energy density e_strain/μ during one complete steady-state oscillation cycle, demonstrating that the asymmetry in the near-tip strain fields is temporally out-of-phase with the instantaneous crack propagation direction (see also Supplementary Movie 1). Simulation parameters in a are the same as in Fig. 3 except the ratio ℓ₀/ξ varying between 0.15 and 2.9. Simulation parameters in b are ℓ₀/ξ = 1.45, H/ξ = 300, W/ξ = 900, G₀/Γ₀ = 3.0 (corresponding to a background strain ɛ_yy = 8.90%), Δ = 0.21ξ and β = 0.28. Simulation parameters in c are the same as in Fig. 2.

Elastic nonlinearity has been found experimentally to also affect the crack-tip shape^21,23,25, which strongly departs at high velocities from the parabolic shape predicted by LEFM. This departure is quantified by the deviation δ of the actual tip location from its predicted location based on the parabolic shape. Figure 4b shows that δ indeed grows dramatically in a narrow range of ultrahigh velocities approaching v_c and can be larger than ℓ₀ in agreement with experiments^8,21,25. As δ is related to ℓ, this result indicates a strong dependence of the latter on velocity. During oscillations, the crack-tip shape and near-tip nonlinear elastic fields become asymmetrical about the instantaneous crack propagation axis on a scale comparable to δ, as illustrated in Fig. 4c, which shows snapshots of the crack-tip shape and strain energy density during one complete steady-state oscillation cycle. This illustrative sequence reveals that the asymmetry in the near-tip strain fields is temporally out-of-phase with the instantaneous crack propagation direction, signalling a breakdown of the principle of local symmetry under dynamic conditions²⁴. How asymmetry on the scale of the nonlinear zone provides an instability mechanism, for example, the one proposed in ref. 24, remains to be further elucidated. Our newly developed nonlinear phase-field model of high-speed cracks provides a unique framework to address this and other fundamental issues, such as the basic relationship of crack oscillations and 3D micro-branching suggested by recent experiments²⁷.

Methods

We use the phase-field framework^16,17 that couples the evolution of the material displacement vector field u(x, y, t) to a scalar field φ(x, y, t) that varies smoothly in space between the fully broken (φ = 0) and pristine (φ = 1) states of the material. The present model is formulated in terms of the Lagrangian L = T − U, where

represent the potential and kinetic energy, respectively, ρ is the mass density inside the pristine material, and dV is a volume element. The form of U implies that the broken state (φ = 0) becomes energetically favoured when the strain energy density e_strain exceeds a threshold e_c, and the function g(φ) = 4φ³ − 3φ⁴ is a monotonously increasing function of φ that controls the softening of elastic energy at large strains. The parameters κ and e_c determine the size of the dissipation zone and the fracture energy in the quasi-static limit^17,18. The evolution equations for φ and u are derived from Lagrange’s equations

for ψ = (φ, u_x, u_y), where the functional

controls the rate of energy dissipation. As shown in the Supplementary Information, it follows from equations (1)–(3) that d(T + U)/dt = −2D ≤ 0. This gradient flow condition implies that the total energy (kinetic + potential) decreases monotonously in time due to energy dissipation near the crack tip where φ varies. In addition, we impose the standard irreversibility condition ∂_tφ ≤ 0.

The above model distinguishes itself from previous phase-field models^26,28 by the formulation of the kinetic energy in equation (1). Previous models exhibit a tip-splitting instability in a velocity range (40% to 55% of c_s depending on the mode of fracture and Poisson’s ratio^26,28) much lower than the velocity in which the oscillatory instability is experimentally observed⁷. Furthermore, tip-splitting generates two symmetrically branched cracks that are qualitatively distinct from both the 3D micro-branching and 2D oscillatory instabilities. Low-velocity tip-splitting can be suppressed by choosing f(φ) in equation (1) to be a monotonously increasing function of φ, similarly to g(φ). In particular, f(φ) = g(φ) (used here) ensures that the wave speeds remain constant inside the dissipation zone, which is physically consistent with the fact that dissipation and structural changes near crack tips in real materials do not involve large modifications of the wave speeds. As the wave speeds control the rate of transport of energy in the dissipation zone, cracks in this model can accelerate to unprecedented velocities approaching c_s, as observed experimentally in quasi-2D geometries⁷.

In addition, unlike conventional phase-field models, we focus on a nonlinear strain energy density given by

where F_ij = δ_ij + ∂_ju_i are the components of the deformation gradient tensor and i, j = {x, y}. It corresponds to a 2D incompressible neo-Hookean constitutive law, exhibiting generic elastic nonlinearities and quantitatively describing the brittle gels in experiments^6,25. In the small-strain limit, neo-Hookean elasticity reduces to standard linear elasticity with a shear modulus μ and a 2D Poisson’s ratio ν = 1/3.

The equations are non-dimensionalized by measuring length in units of ξ and time in units of τ = 1/(2χe_c), characterizing the timescale of energy dissipation. Crack dynamics is then controlled by only two dimensionless parameters: e_c/μ and β ≡ τc_s/ξ. The first controls the ratio ℓ₀/ξ = 2.9e_c/μ, where ℓ₀ = Γ₀/μ sets the size of the nonlinear zone where elasticity breaks down (Fig. 1). The second controls the velocity dependence of the fracture energy. In the ideal brittle limit, β ≪ 1, Γ(v) ≈ Γ₀ is independent of v. In the opposite limit, β ≫ 1, dissipation is sluggish and Γ(v) is a strongly increasing function of v. We vary e_c/μ between 0.05 and 1.0 to control the importance of elastic nonlinearity and choose a value β = 0.28 so that Γ(v)/Γ₀ increases by about 20% when v varies from zero to v_c (see the inset of Supplementary Fig. 4), in qualitative similarity to experiments²⁵. The equations are discretized in space on a uniform square mesh with a grid spacing Δ = 0.21ξ and finite-difference approximations of spatial derivatives, and integrated in time using a Beeman’s scheme (see Supplementary Information) with a time-step size Δt = 5 × 10⁻⁴ τ. Large-scale simulations of 10⁶–10⁷ grid points are performed using graphics processing units with the CUDA parallel programming language.

LEFM has been experimentally validated for accelerating cracks that follow straight trajectories, prior to the onset of instabilities^15,29. Therefore, as a quantitative test of our high-speed crack model (see Supplementary Information), we verified the predictions of LEFM by showing that an accelerating crack centred inside a strip (as illustrated in Supplementary Fig. 3) satisfies the scalar equation of motion G = Γ(v), as long as their trajectory remains straight (v < v_c). We performed this test for the nonlinear form of e_strain defined by equation (4) by monitoring the instantaneous total crack length a (distinct from the crack-tip propagation distance d plotted in Figs 2 and 3), crack velocity v, and energy release rate G calculated directly by contour integration using the J-integral (see Supplementary Information). The results show that cracks accelerated under different loads G₀/Γ₀ exhibit dramatically different v versus a curves (Supplementary Fig. 4), but the same G versus v curves (inset of Supplementary Fig. 4), which define a unique fracture energy Γ(v) (independent of the external load and crack acceleration history). Those results are consistent with the theoretical expectation that the relation G = Γ(v), which simply accounts for energy balance near the crack tip, should remain valid even in the presence of elastic nonlinearity as long as G is calculated through the J-integral evaluated in a non-dissipative region.

To investigate crack instabilities, we carried out simulations using a treadmill method^19,26 that maintains the crack tip in the centre of the strip by periodically adding a strained layer at the right vertical boundary ahead of the crack tip and removing a layer at the opposite left boundary. This method allows us to study large crack propagation distances by mimicking an infinite strip with negligible influence of boundary effects. To further support the results presented in the main text, we carried out additional simulations to verify that the oscillation wavelength is independent of the choice of the degradation function g(φ) (Supplementary Fig. 5) and the grid spacing Δ (Supplementary Fig. 6).

Code availability.

The CUDA implementation of the phase-field simulation code is available upon request.

Data availability.

The data that support the plots within this paper and other findings of this study are available from one of the corresponding authors (A. Karma) upon reasonable request.