Abstract
The electronic capacitance of a one-dimensional system such as a carbon nanotube is a thermodynamic quantity that contains fundamental information about the ground state1. It is composed of an electrostatic component describing the interactions between electrons and their correlations, and a kinetic term given by the electronic density of states. Here, we use a field-effect transistor geometry to obtain the first direct capacitance measurement of individual carbon nanotubes, as a function of the carrier density. Our measurements detect the electrostatic part of the capacitance as well as the quantum corrections arising from the electronic density of states. We identify the van-Hove singularities that correspond to the one-dimensional electron and hole sub-bands and show that the measured capacitance exhibits clear electron–hole symmetry. Finally, our measurements suggest the existence of a negative capacitance, which has recently been predicted to exist in one dimension as a result of interactions between electrons2,3,4.
Similar content being viewed by others
Main
The capacitance of a classical conductor is determined solely by its geometry. When charged, the electrons distribute in space in a manner that minimizes their electrostatic energy. Quantum mechanics introduces extra energies that add new contributions to the capacitance. As the energies simply add and capacitance is inversely proportional to energy, these contributions add in series with the classical geometric capacitance (Cg) to yield the total capacitance, Ctot−1=Cg−1+Cdos−1+Cxc−1. The first contribution is caused by the kinetic energy of the electrons. Adding electrons to a conductor requires finite kinetic energy and therefore adds a term (Cdos) that reduces the total capacitance. The second contribution results from the correlated motion of electrons, which generally leads to reduction of their total electrostatic energy1,5,6. This adds a negative capacitance term (Cxc) that increases the total capacitance. The density dependence of these terms captures the fundamental properties of the quantum ground state and their measurements in two-dimensional systems7,8,9,10,11 established the role of interactions in the ground state.
In one dimension, the capacitance plays a special role as it also determines the properties of the excitations. Described within the Luttinger model12, the fundamental excitations are collective waves of spin or charge. Electronic interactions lift the degeneracy of these modes by enhancing the velocity of the charge excitations by a factor g−1, the inverse Luttinger parameter. This electrostatic effect is captured by the compressibility of the electronic gas13, or equivalently by its capacitance2,14. Thus, the central parameter of the Luttinger liquid theory is directly related to the capacitance by the simple relation  . So far, g has been inferred mostly from transport measurements15,16,17,18,19,20 that probe the electronic excitations. Capacitance allows an independent thermodynamic determination of this parameter and its density dependence.
. So far, g has been inferred mostly from transport measurements15,16,17,18,19,20 that probe the electronic excitations. Capacitance allows an independent thermodynamic determination of this parameter and its density dependence.
In this work we present the first direct capacitance measurements of carbon nanotubes (NT). A NT strongly coupled to a metallic gate forms a capacitor with a rigid geometry whose geometric and quantum capacitances are comparable, allowing us to extract both quantitatively. The measured geometrical capacitances are consistent with the classical expression for the capacitance between a gate and a wire. The observed quantum corrections demonstrate a symmetric one-dimensional sub-band structure of electrons and holes and yield g in the NT. Deviations of the measured capacitance from a theory that includes interactions only at Hartree mean-field level points to the importance of electron correlations.
We use top-gated semiconducting single-wall NT devices (Fig. 1a,b) in which the capacitor is formed between the top gate and the NT segment beneath it. The two side NT segments act as its leads. Figure 2 shows the measured transport of a top-gated device (T=77 K in all measurements reported in this paper). The source–drain conductivity, G=dI/dV, is plotted as a function of top-gate voltage, Vtg, which controls the density in the central NT segment, and back-gate voltage, Vbg, which tunes the density in the NT leads. The four corners in this plot are marked nnn, npn, pnp and ppp to reflect the carrier polarity in the NT leads and the central segment. Good conductivity is observed whenever the leads have the same polarity as the central segment (ppp and nnn corners). Therefore, to measure the capacitance in the n and p sides we tune the leads to be n or p type respectively to ensure that the contact resistance does not limit the charging of the NT (R≪100 GΩ).
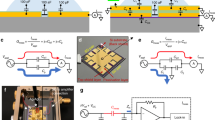
a, Illustration of the NT capacitor device. The capacitance is measured between the top gate and the NT with both source and drain electrodes shorted. b, AFM image of an actual device. The NT is visible under the top gate, allowing accurate determination of the effective capacitor length. c, Schematic diagram of the capacitance bridge measurement circuit. d, Theoretical density of states of a semiconducting NT as a function of the Fermi energy at zero temperature. The first two electron and hole sub-bands are shown. Each sub-band gives a van-Hove singularity followed by a slow decrease of the density of states.
The conductance, G=dI/dV, is plotted against top-gate voltage, Vtg, and back-gate voltage, Vbg, on a logarithmic scale. The top gate tunes the density of the NT segment beneath it, whereas the back gate controls the density of the two side segments, referred to as NT leads. The corners are labelled ppp, pnp, npn and nnn to reflect the polarities of the charge carriers in the NT leads and the central segment. The dashed blue lines mark the turn-on of conductivity due to the NT leads, which depends on the electron density in the leads, set solely by Vbg. At large electron (Vbg>4 V) or hole (Vbg<−4 V) densities the leads are conductive. The dashed red lines mark the turn-on of the conductivity due to the central NT segment. This turn-on depends only on the electron density in the central segment. This density is predominantly determined by the voltage on the near top gate (10 nm), however, it is also slightly influenced by the distant back gate (200 nm). The ratio of the top- and back-gate couplings is determined from the slopes of the dashed red lines, both yielding dVtg/dVbg=0.04.
Now we turn to the capacitance measurements and demonstrate how the NT capacitance is accurately differentiated from the background stray capacitance, C0. To this end, we exploit the tunability of the NT leads to carry out two independent capacitance measurements, one with and one without the NT central segment electrically connected to the measurement circuit. This is done by back-gating the NT leads into their semiconducting gap to increase their resistance to immeasurably large values. Consequently, the RC time to charge the central segment becomes too large and its capacitance drops from the measurement. In the inset of Fig. 3, we plot the capacitance measured as a function of Vbg at a fixed Vtg. The capacitance is constant at high Vbg, drops sharply around Vbg≈−4 V and remains constant at lower voltages. Comparing this with the transport measured on the same device (Fig. 2), the drop is associated with the leads becoming resistive (R≫100 GΩ). Thus, at low voltages the stray capacitance is measured. The NT capacitance, CNT, is then accurately determined from the measured capacitance step.
The NT capacitance, CNT versus capacitor length, L, for eight devices (blue circles). The capacitor length is extracted from the AFM images. The red lines are the calculated classical geometric capacitance between a conducting plane and wire separated by 10 nm of SiOx, for diameters d=1 nm and 4 nm. Top inset: Capacitance of the NT device measured as function of back-gate voltage Vbg, at a fixed top-gate voltage. At low negative Vbg, the NT capacitor is effectively disconnected from the measurement circuit (bottom right illustration) and the background capacitance, C0, is measured. CNT, is determined from the capacitance step (see the text).
In Fig. 3 we show CNT measured in this manner for eight NT devices, plotted against the length of the NT extracted from the atomic force microscopy (AFM) images. We also plot the classical expression for the capacitance between a metallic wire and a metallic plane:

where d and L are the wire diameter and length, h is the separation and the dielectric permittivity ɛ=3.9ɛ0 for SiOx. Two curves are shown, corresponding to d=1 nm and 4 nm, spanning the diameter range of our devices. We can see that the simple geometric formula describes the measured capacitances reasonably well.
Now we turn to the main result of this paper—the dependence of the NT capacitance on the carrier density, n. Figure 4a shows the measured capacitance as a function of Vtg. The cyan curve (NT leads pinched-off, Vbg=0) gives the baseline stray capacitance, which is independent of Vtg. In contrast, with n- or p-type leads (Vbg=+7 V/−7 V red/blue curves respectively) the capacitance has a well-pronounced structure—a large dip in the centre followed by symmetric structures at its positive and negative sides. Comparing this with the transport measured on the same device (Fig. 4b), the large dip is associated with the semiconducting gap. Outside the gap, the capacitance decreases slowly on both sides of the gap and then rises rapidly at symmetric locations with respect to the gap centre (Vtg≈+0.2 V,−3.6 V). At positive voltages we observe a second slow decrease following the sharp rise.
The top gate controls the carrier density of the NT segment in the capacitor (bottom left illustration). a, CNT measured as a function of Vtg at three different states of the NT leads: Vbg=0 V, pinched off leads (cyan); Vbg=+7 V, n-type leads (red); and Vbg=−7 V, p-type leads (blue). We corrected for the back-gate-induced carrier density change in the central NT segment by shifting the red/blue curves by ΔVtg=±7 V×0.04=±0.28 V, where we used the ratio of top and back-gate coupling extracted from transport (dashed red lines in Fig. 2). We note that after this parameter-free shift, the large capacitance dips in the electron and hole curves overlap. The dashed black curve corresponds to the theoretical Hartree prediction with T=77 K and no disorder. b, The conductance, G, measured on the same device using the same gate voltages as in a, n-type contacts, Vbg=+7 V (red) and p-type contacts, Vbg=−7 V (blue).
Notably, there is a strong similarity between the voltage dependence of the capacitance on the electron and hole sides. To demonstrate this further, in Fig. 5 we overlay the measured capacitance in the electron side (red) with that of the hole side, reflected around the centre of the gap (blue). The two curves show an excellent agreement to within our measurement accuracy. This symmetry is notable if we realize that there is no inherent symmetry in the actual device parameters—at zero Vtg the device is strongly n type and therefore significantly different top-gate voltages are used to access the electron and hole sides.
The measured top-gate dependence of CNT in the electron side (red) overlaid with the measured hole-side dependence reflected around the centre of the large gap (Vtg=−1.70 V) (blue). The error bars represent the accuracy determined from the averaging time. The Hartree (dashed black) and Hartree–Fock (dashed green) curves both calculated at T=77 K with no disorder are also shown. Inset: The Luttinger parameter,  , as a function of carrier density, n, in the first sub-band deduced from the measured capacitance of electrons (red) and holes (blue).
, as a function of carrier density, n, in the first sub-band deduced from the measured capacitance of electrons (red) and holes (blue).
The observed voltage dependence reflects the density of states of the one-dimensional sub-bands in the NT (Fig. 1d). Each sub-band gives rise to a sharp van-Hove singularity followed by a slow decrease of the density of states. These are manifested as sharp rises and slow decreases in the capacitance, where electron and hole sub-bands appear at opposite sides of the bandgap (qualitative evidence for sub-bands was recently seen21 in the local capacitance measured by AFM). The observed electron–hole symmetry of the capacitance reflects the underlying electron–hole symmetry in the band structure of the NT22 and demonstrates that it persists even in the presence of disorder.
To analyse our data quantitatively we begin with a simple Hartree model that consists of the density of states capacitance, a constant geometric capacitance and no electronic correlations:

The density of states capacitance at a given chemical potential, μ, and temperature, T, is given by:

where we included the first two electron and hole sub-bands, ħ is the reduced Planck’s constant, vF=8×105 m s−1 is the Fermi velocity and f′ is the derivative of the Fermi function. In the experiment, the total capacitance is measured as a function of gate voltage rather than the Fermi energy. We note that the conversion ratio between these two quantities is fully determined by the capacitances:

Combining equations (2)–(4), we get an expression for the gate dependence of the total capacitance at finite temperatures, Ctot(Vtg,T), which is plotted for T=77 K in Figs 4a and 5 (dashed black line). By matching the theory and data at a single point (bottom of second sub-band step), we exhaust the free parameters of the theory, Cg and d, and the entire functional dependence is then fully determined. The overall structure of the measured capacitance is reproduced very well within the Hartree theory. The extracted parameters, d=2.35 nm and Cg=61.5 aF μm−1, compare favourably with the AFM-measured diameter d=2.5±0.5 nm and the capacitance C=76.5 aF μm−1 calculated with equation (1).
Near the semiconducting gap (−2.4 V<Vtg<−1 V) the measured capacitance deviates significantly from the theory. The reason becomes apparent when we compare it with the transport measured on the same device (Fig. 4b). The deviations are observed whenever the device is resistive (R≥100 GΩ) and consequently the capacitor does not charge completely. From comparison to theory, the capacitance roll-off happens at a finite density, n0≈200 e μm−1, corresponding to a Fermi energy of Ef∼30 mV. By comparing this with the transport data we conclude that the NT transistor turns off not when the tube is fully depleted of carriers, but when the barriers associated with disorder lead to an exponentially decreasing conductivity.
A fundamental quantity that can be readily determined from the capacitance measurement is g. In previous transport experiments15,16,17,18,19,20 this parameter has been deduced through its effects on the electronic excitations. Here we use the imprint of g on a thermodynamic property, the capacitance, to determine this parameter and its density dependence in a semiconducting NT. In the inset of Fig. 5 we plot the derived  as a function of the density of electrons (red) and holes (blue) in the first sub-band. The observed g changes continuously with density over a large range: g=0.26–0.34. These values are consistent with those deduced from transport experiments in NTs15,16,17,18 and predicted theoretically23,24.
as a function of the density of electrons (red) and holes (blue) in the first sub-band. The observed g changes continuously with density over a large range: g=0.26–0.34. These values are consistent with those deduced from transport experiments in NTs15,16,17,18 and predicted theoretically23,24.
Although the Hartree theory gives a reasonable account of the data, quantitative deviations can be seen when we compare them in detail (Fig. 5). In both sub-bands, the measured voltage dependence of the capacitance, dC/dVtg, is significantly steeper. In addition, the measured capacitance step at the opening of the second sub-band is significantly higher (∼40%). These deviations are much larger than our measurement uncertainty or any detectable deviations between electrons and holes. Adding disorder to the Hartree theory will decrease its predicted step height and will only increase the discrepancy between the theory and the measurement.
A possible explanation for the observed deviations is given by electronic exchange and correlations. These add a third term to the capacitance, Cxc, which is predicted2,3 to be negative at low densities. Consequently, whenever a new sub-band opens, it adds a new negative Cxc term to the capacitance. As this term adds in series, it will increase the total capacitance just after the opening of the sub-band, producing an upward step of the capacitance concurrent with the sub-band opening. This correlation-induced step should therefore increase the capacitance step beyond the Hartree prediction. This is exactly what we see in the opening of the second sub-band. It is also predicted2,3 that Cxc−1 decreases with increasing density and smoothly crosses over to positive values at high densities. This effect will decrease the total capacitance with density faster than expected from the Hartree theory, also in accordance with the data. To make a quantitative comparison, we add the leading correction to our theory by accounting for exchange effects (see Supplementary Information, note 1) and plot the resulting Hartree–Fock curve (green dashed line) in Fig. 5. Indeed, both the predicted C step and its derivative dC/dVtg become larger. However, although the Hartree–Fock approximation correctly captures the density dependence in the first sub-band, the predicted effect in the second sub-band is exaggerated compared with the measurement. Including the effect of disorder in the Hartree–Fock theory, which in contrast to the Hartree case will improve its agreement with the measurement, as well as a more complete treatment of electron correlations (Hartree–Fock is known to overestimate correlations) will be needed to explain our observations.
Methods
Device fabrication
The devices used in this study use a metallic top-gate separated from a NT by a thin layer of oxide to form a capacitor (Fig. 1a). The NTs were grown using chemical vapour deposition from patterned pads of evaporated Fe on degenerately doped silicon with a 200 nm SiO2 top layer. We used a C2H4/H2 growth recipe, which we found to produce predominantly single-walled NTs with small diameters (1–4 nm). After growth, the NTs were contacted with source and drain electrodes made of 50 nm of palladium, followed by aligned deposition of 10 nm SiOx dielectric and 50 nm aluminium top gate. This geometry enables us to carry out transport as well as capacitance measurements on the same device. All devices were imaged with AFM before their capacitance/transport measurements to ensure that only a single tube passes under the top gate. Figure 1b shows a typical image after the full fabrication sequence. All the measurements reported in this paper were done on semiconducting NTs at T=77 K.
Capacitance measurements
The NT capacitances are measured using a capacitance bridge (Fig. 1c). The NT capacitor is embedded in the measurement arm of the bridge. A fixed a.c. voltage excitation (δ Vmeas∼=25–100 mV) along this arm is balanced against a second excitation along the reference arm (δ Vref∼) to null the voltage oscillations at the balance point B. Under these conditions, the measured capacitance is Cmeas=Crefδ Vref∼/δ Vmeas∼ and the large stray capacitances between the leads of the NT capacitor and ground (CS1,CS2) are cancelled out. Direct capacitive coupling between the wiring is eliminated using shielded wires and by encapsulating the device in a Faraday cage. The direct capacitance between the on-chip gate and contact electrodes is shielded by a nearby back gate. After these steps, we are left with only a few hundred aF of fixed background capacitance. The measurements reported in this paper are done at 1 kHz. With a bridge sensitivity of  and long averaging times we achieve a noise level smaller than 1 aF in these measurements.
and long averaging times we achieve a noise level smaller than 1 aF in these measurements.
References
Mahan, G. D. Many-Particle Physics (Plenum, New York, 1990).
Glazman, L. I., Ruzin, I. M. & Shklovskii, B. I. Quantum transport and pinning of a one-dimensional Wigner crystal. Phys. Rev. B 45, 8454–8463 (1992).
Fogler, M. M. Ground-state energy of the electron liquid in ultrathin wires. Phys. Rev. Lett. 94, 056405 (2005).
Latessa, L., Pecchia, A., Di Carlo, A. & Lugli, P. Negative quantum capacitance of gated carbon nanotubes. Phys. Rev. B 72, 035455 (2005).
Bello, M. S., Levin, E. I., Shklovskii, B. I. & Efros, A. L. Density of localized states in the surface impurity band of a metal-dielectric-semiconductor structure. Zh. Eksp. Teor. Fiz. 80, 1596–1612 (1981) [JETP 53, 822 (1981)].
Efros, A. L. Density of states of 2D electron-gas and width of the plateau of IQHE. Solid State Commun. 65, 1281–1284 (1988).
Smith, T. P., Wang, W. I. & Stiles, P. J. Two-dimensional density of states in the extreme quantum limit. Phys. Rev. B 34, 2995–2998 (1986).
Mosser, V., Weiss, D., von Klitzing, K., Ploog, K. & Weimann, G. Density of states of GaAs-AlGaAs-heterostructures deduced from temperature-dependent magnetocapacitance measurements. Solid State Commun. 58, 5–7 (1986).
Kravchenko, S. V., Rinberg, D. A., Semenchinsky, S. G. & Pudalov, V. M. Evidence for the influence of electron-electron interaction on the chemical-potential of the two-dimensional electron-gas. Phys. Rev. B 42, 3741–3744 (1990).
Luryi, S. Quantum capacitance devices. Appl. Phys. Lett. 52, 501–503 (1988).
Eisenstein, J. P., Pfeiffer, L. N. & West, K. W. Negative compressibility of interacting two-dimensional electron and quasi-particle gases. Phys. Rev. Lett. 68, 674–677 (1992).
Haldane, F. D. M. Luttinger liquid theory of one-dimensional quantum fluids I: Properties of the Luttinger model and their extension to the general 1d interacting spinless Fermi gas. J. Phys. C: Solid State Phys. 14, 2585–2609 (1981).
Haldane, F. D. M. Effective harmonic-fluid approach to low-energy properties of one-dimensional quantum fluids. Phys. Rev. Lett. 47, 1840–1843 (1981).
Bockrath, M. W. Carbon Nanotubes: Electrons in One Dimension. Thesis. Univ. California, Berkeley (1999).
Bockrath, M. et al. Luttinger-liquid behaviour in carbon nanotubes. Nature 397, 598–601 (1999).
Yao, Z., Postma, H. W. C., Balents, L. & Dekker, C. Carbon nanotube intramolecular junctions. Nature 402, 273–276 (1999).
Postma, H. W. C., de Jonge, M., Yao, Z. & Dekker, C. Electrical transport through carbon nanotube junctions created by mechanical manipulation. Phys. Rev. B 62, 10653–10656 (2000).
Postma, H. W. C., Teepen, T., Yao, Z., Grifoni, M. & Dekker, C. Carbon nanotube single-electron transistors at room temperature. Science 293, 76–79 (2001).
Auslaender, O. M. et al. Experimental evidence for resonant tunneling in a Luttinger liquid. Phys. Rev. Lett. 84, 1764–1767 (2000).
Auslaender, O. M. et al. Spin-charge separation and localization in one dimension. Science 308, 88–92 (2005).
Heo, J. S. & Bockrath, M. Local electronic structure of single-walled carbon nanotubes from electrostatic force microscopy. Nano Lett. 5, 853–857 (2005).
Jarillo-Herrero, P., Sapmaz, S., Dekker, C., Kouwenhoven, L. P. & van der Zant, H. S. J. Electron-hole symmetry in a semiconducting carbon nanotube quantum dot. Nature 429, 389–392 (2004).
Egger, R. & Gogolin, A. O. Effective low-energy theory for correlated carbon nanotubes. Phys. Rev. Lett. 79, 5082–5085 (1997).
Kane, C., Balents, L. & Fisher, M. P. A. Coulomb interactions and mesoscopic effects in carbon nanotubes. Phys. Rev. Lett. 79, 5086–5089 (1997).
Acknowledgements
We thank P. Brouwer, E. Mueller and S. Tiwari for discussions. This work was supported by the NSF through the Cornell Center for Material Research and the Center for Nanoscale systems, and by the MARCO Focused Research Center on Materials, Structures and Devices. Sample fabrication was carried out at the Cornell node of the National Nanofabrication Users Network, funded by NSF. M.K. acknowledges support by the Packard Foundation.
Author information
Authors and Affiliations
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Rights and permissions
About this article
Cite this article
Ilani, S., Donev, L., Kindermann, M. et al. Measurement of the quantum capacitance of interacting electrons in carbon nanotubes. Nature Phys 2, 687–691 (2006). https://doi.org/10.1038/nphys412
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys412
This article is cited by
-
One-dimensional semimetal contacts to two-dimensional semiconductors
Nature Communications (2023)
-
Complementary carbon nanotube metal–oxide–semiconductor field-effect transistors with localized solid-state extension doping
Nature Electronics (2023)
-
Resonant exciton transfer in mixed-dimensional heterostructures for overcoming dimensional restrictions in optical processes
Nature Communications (2023)
-
Inferring the energy sensitivity and band gap of electronic transport in a network of carbon nanotubes
Scientific Reports (2022)
-
Ionic gate spectroscopy of 2D semiconductors
Nature Reviews Physics (2021)