Abstract
The scattering of electrons in dielectric materials is central to laser nanomachining1, light-driven electronics2 and radiation damage3,4,5. Here, we demonstrate real-time access to electron scattering by implementing attosecond streaking spectroscopy on dielectric nanoparticles: photoelectrons are generated inside the nanoparticles and both their transport through the material and photoemission are tracked on an attosecond timescale. We develop a theoretical framework for attosecond streaking spectroscopy in dielectrics and identify that the presence of the internal field inside the material cancels the influence of elastic scattering, enabling the selective characterization of the inelastic scattering time. The approach is demonstrated on silica nanoparticles, where an inelastic mean-free path is extracted for 20–30 eV. Our approach enables the characterization of inelastic scattering in various dielectric solids and liquids, including water, which can be studied in the form of droplets.
Similar content being viewed by others
Main
The interaction of a dielectric material with photons that have above-bandgap energies inevitably leads to the production of hot electrons propagating through the material. During propagation these electrons can undergo a number of elastic and inelastic scattering events. The inelastic scattering of such electrons can give rise to rapid carrier multiplication via impact ionization, enabling laser nanomachining1 and limiting the scaling of electronic signal processing towards optical (petahertz-scale) frequencies using extremely strong electric fields2 by dielectric breakdown. Moreover, secondary electrons represent the main source of radiation damage following tissue irradiation. Thus, knowledge of inelastic electron scattering in a dielectric, such as liquid water, is essential to fully understand how radiation affects living organisms3,4,5.
To understand the phenomena above, we must be able to study collision dynamics in dielectrics for energies ranging from the bandgap energy up to the hard-X-ray regime. However, methods for measuring collision dynamics have been mostly limited to electron energies above ≍50 eV (ref. 6). These methods include the measurement of inelastic mean-free paths (IMFPs), where a mean-free path is the average distance that an electron will travel in a solid between adjacent collision events. Standard IMFP measurements are based on the dielectric description of inelastic scattering of charged particles in condensed matter7 and elastic peak electron spectroscopy. While progress has been made toward determining IMFPs for very low kinetic energy (of a few electronvolts) by angle-resolved photoelectron spectroscopy8, data in the tens-of-electronvolt range, where the impact ionization of valence-band electrons strongly dominates the IMFP, are largely missing. Moreover, amorphous dielectric solids such as SiO2 and liquid water, which can be accessed with our approach, are challenging for rigorous ab initio calculations of IMFPs.
For electron energies in the tens-of-electronvolt range, collisions typically occur in the sub-femtosecond range. We have access to this timescale via attosecond streaking9: photoemission inside a solid is initiated by an extreme ultraviolet (XUV) pulse, and the momentum change of released electrons due to a second near-infrared (NIR) pulse is measured as a function of XUV/NIR pulse delay (see Supplementary Information). To date, this metrology has been applied only to metals10,11,12,13,14,15,16,17,18,19 or adlayer-covered metals20,21, where the NIR streaking field takes effect only on the surface of the material. The physics for dielectrics, however, is fundamentally different as the released electrons are streaked by the NIR field also inside the solid. Most importantly, until now accumulative charging induced by the XUV pulse has prevented the application of attosecond streaking to dielectrics. Here, we solve this problem by using a continuous stream of nanoscopic targets. Our proof-of-concept study was focused on silicon dioxide, the most important dielectric material in microelectronics and optics.
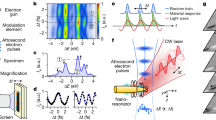
In the experiment depicted in Fig. 1, a stream of isolated 50-nm, SiO2 nanospheres was delivered into the laser interaction region by aerodynamic lens focusing22,23,24,25,26. Emitted electrons were detected by a kilohertz, single-shot velocity-map imaging spectrometer. This set-up can differentiate images that contain only reference gas from those with nanoparticles, as reference-gas-only frames contain significantly fewer electrons than do those containing nanoparticles (see Fig. 2a). Further frame selection was obtained by taking into account the asymmetric momentum distribution of nanoparticle electrons originating from shadowing22,25,27 of the XUV field, thus providing an efficient sorting method (see Fig. 2b, c). This data discrimination provided us with nanoparticle and reference streaking spectrograms (such as those in Fig. 3) from the very same experimental data set, that is, for identical laser conditions from a single pulse delay scan. Figure 2d, e shows discriminated momentum data, averaged over millions of shots, for the reference medium and nanoparticles, respectively.
A beam of isolated nanoparticles is hit by isolated attosecond XUV pulses and synchronized few-cycle NIR pulses. Emitted electrons are recorded with a velocity-map imaging (VMI) spectrometer. Right inset: Transmission electron micrograph of the SiO2 nanoparticles. Left inset: Mie calculation of the XUV attenuation (shadowing).
a, Histogram of the events per shot measured for residual gas only and with SiO2 nanoparticles (as indicated). b,c, Typical single-shot images containing contributions from the residual gas only (b) and nanoparticles (c) measured for zero delay. Photoelectrons emitted from nanoparticles exhibit asymmetric momentum distributions that originate from XUV shadowing. d,e, Respective averaged momentum distributions measured for zero delay. For low momenta (<0.75 a.u., inside the dashed circles) the signal contains additional background contribution (see Supplementary Information).
a–c, Attosecond spectrograms measured for residual gas and nanoparticles and as predicted by M3C simulations (as indicated) obtained from angular integration of projected momentum maps over ±25° around the laser polarization direction (see Fig. 2d, e and Supplementary Information for details). For the relative delay analysis energy-dependent frequency-filtered isolines were fitted with few-cycle waveforms, whose carrier phases define the streaking delay δt (see symbols and curves in a–c, see Supplementary Information for details). d, Energy-dependent streaking delays measured for residual gas (blue symbols) and nanoparticles (red symbols). The data represent an average over three scans performed under similar conditions (error bars indicate the deviation of the individual data sets). Solid lines show corresponding simulation results for gas (blue), nanoparticles (black) and their mixture (red) using an XUV chirp of −7 × 10−3 fs2. Inset: Relative contribution of electrons without inelastic collisions in the M3C simulations. e, Measured energy-dependent ratio of nanoparticle signal relative to residual gas (red) and result obtained from combining simulated gas and nanoparticle spectrograms (black).
When analysed as a function of the delay of the NIR with respect to the XUV pulses, Δt, electron kinetic energy spectra derived from the projected momentum form streaking spectrograms with pronounced delay-dependent oscillations for gas and nanoparticles (see Fig. 3a, b). The gas reference essentially reflects the NIR pulse vector potential. It further includes temporal shifts due to the Wigner delay28 and effects from Coulomb-laser coupling29,30. As the long-range potentials of gas and nanoparticles are both Coulomb-like, these shifts are assumed comparable for gas and nanoparticles. They effectively cancel each other in the relative delay between the spectrograms, up to remaining short-range effects that are assumed small away from resonances31. To extract the delays, we consider isocontour lines for different asymptotic energies (for example, blue and red dotted lines for 25 eV). Individual energy-dependent streaking delays are determined from fits to the respective filtered contour lines (see Supplementary Information). The streaking delays for SiO2 and δtgas for the reference gas (symbols in Fig. 3d) exhibit similar energy-dependent tilts, which are attributed to the XUV pulse properties (XUV chirp, see Supplementary Information for details). Measured nanoparticle frames still contain a small contribution from residual gas (see Fig. 3e).
We simulated electron emission from nanoparticles by trajectory-based mean-field Mie Monte Carlo transport calculations (M3C; ref. 32). XUV photoelectrons generated inside the material are propagated in the NIR near field of the particle and experience elastic and inelastic collisions that have energy-dependent cross-sections (see Supplementary Information for details). The energy-dependent streaking delays, , extracted from simulated streaking spectrograms for pure nanoparticles (Fig. 3c) exhibit a tilt similar to that of the experiments (black line in Fig. 3d) and a global relative streaking delay with respect to the delay, δtgas, calculated for gas. The gas data (blue symbols) can be fully reproduced (blue line) by taking into account the XUV chirp.
For a quantitative comparison, we combined simulated spectrograms of gas and nanoparticles using a single mixing factor such that the signal ratio found in the experiments is reproduced (see Fig. 3e). Streaking delays extracted from this mixed nanoparticle data (red line in Fig. 3d) show good agreement with the experiment. This supports that the model accurately reflects the relevant phenomena under scrutiny and that other factors are of minor importance.
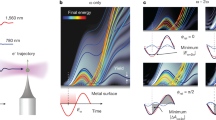
The agreement between the experimental data and simulation results motivates a closer analysis of contributions to the relative streaking delay to gain insight into the relevant processes. The first two contributions to the absolute SiO2 streaking delay δ = δtoffset + δtchirp + δtfields + δtcoll describe the carrier-envelope phase of the streaking field plus the XUV–NIR delay axis offset (δtoffset) and the XUV chirp (δtchirp). These two terms represent the residual gas delay and thus cancel out in the resulting relative streaking delay δtrel = δ − δtgas = δtfields + δtcoll (see Supplementary Information for details). Since the contribution δtfields, characterizing the retardation and inhomogeneity effects of the NIR and XUV near fields, is negligible (see Supplementary Information), the remaining term from electron scattering within the solid, δtcoll, provides the dominant contribution that is illustrated in Fig. 4. In the relevant energy range, interband excitations constitute the dominant inelastic scattering channel33 and result in an energy loss comparable to the bandgap energy (≍9 eV for SiO2), removing the inelastically scattered electrons from the spectral region of interest, that is, the high-energy part of the streaking trace. We therefore focus on electrons without inelastic collisions, which determine the high-energy signals (see inset of Fig. 3d). For clarity, we discuss the effect for a fully transparent material (unit permittivity). Electrons with charge q generated at time t0 with initial momentum p0 have a final momentum pf = p0 + q A(t0) after escaping along the surface normal (green arrow in Fig. 4a) without any collisions. Here A(t) is the vector potential whose tangential components are assumed to be zero. The streaking trace that results from these directly emitted electrons (green curve in Fig. 4b) characterizes the streaking field vector potential, A(t), and is thus equivalent to gas-only traces.
a, Photoemission of electrons generated at time t0 with initial momentum p0 from an ideal transparent material (unit permittivity) without collisions (green) and following an elastic collision (red) at time tc after propagation inside the material (blue arrow). b, The final momentum pf = |p0|n + q A(t0) for unscattered electrons with charge q emitted parallel to the surface normal n reflects the NIR pulse vector potential A(t) = A0ncos(ω[t − Δt]), resulting in a streaking trace with delay δt = 0 (green curve). Elastically scattered electrons gain a momentum Δp = q[A(t0) − A(tc)] during propagation in the laboratory frame before the ingoing collision momentum pc = p0 + Δp is directionally randomized. The final momentum for normal emission becomes pf = |pc|n + q A(tc). For an electron ensemble with isotropic initial momenta p0, the shift Δp is distributed isotropically and thus roughly cancels on average in the initial momentum frame (see Supplementary Information) such that 〈pc〉 ≍ p0 for Δp ≪ p0. The average final momentum for normal emission is 〈pf〉 ≍ |p0|n + q A(tc). The mean streaking trace is essentially shifted by δt ≍ tc compared with the direct emission (red versus green curve). c, Population of electrons without inelastic collisions leading to time-shifted contributions to the final streaking spectrogram.
In contrast, electrons that leave after elastic, isotropic scattering at time tc (red symbol in Fig. 4a) are essentially indistinguishable from direct electrons generated at time tc (see Supplementary Information for details). Each elastic collision acts as a new ‘birth’ for an electron such that electrons with final elastic scattering time tc have an average final momentum 〈pf〉 ≍ p0 + q A(tc), yielding a streaking trace shifted by tc (red curve in Fig. 4b). The final spectrogram is an average of shifted streaking traces, each weighted with the corresponding emission current. As the emission current reflects the population decay resulting from interband excitations, the streaking delay is very sensitive to the inelastic scattering time (Fig. 4c).
M3C simulations with varying scattering parameters reveal the quantitative effects of elastic and inelastic scattering on the relative streaking delays (Fig. 5a), namely a weak dependence on the elastic scattering time, and a strong dependence on the inelastic scattering time. The impact of a material’s permittivity at the streaking field wavelength is shown in Fig. 5b. Irrespective of the permittivity, represented by the field attenuation factor α = 1/ɛr, the streaking delay increases with inelastic scattering time. However, in both the transparent (α → 1) and the metal (α → 0) limits, the delays remain strongly influenced by the elastic scattering time. With increasing elastic scattering time, delays decrease toward the transparent limit but increase toward the metallic limit. These opposing trends reflect the effect of the internal field attenuation and, most importantly, almost vanish for α ≍ 0.3. The identification of this cancellation is one of the major results of our analysis as it enables the direct retrieval of inelastic scattering times for a range of dielectric materials. The streaking delay’s high sensitivity to the inelastic collision time justifies its extraction from the full M3C simulations, which match the experimental data in Fig. 3d using a scaled Lotz cross-section. We find τinel ∼ 370 as at 25 eV in SiO2. Figure 5c shows comparison of the resulting electron IMFP in SiO2 obtained here between 20 and 30 eV with results found in the literature6,34,35,36. Note that best agreement is found with the work reported in ref. 34, where the authors state that their data in the range of 10–40 eV are unreliable and serve only as a trend. With IMFPs obtained via the demonstrated approach the predictive capability of theoretical models for scattering in dielectrics can now be thoroughly tested.
a, Streaking delays for 50 nm SiO2 nanoparticles calculated from M3C for varying elastic and inelastic scattering times (as indicated). For clarity, we considered unchirped XUV pulses, non-dispersive material, and energy-independent inelastic and elastic scattering times, τinel and τel, resulting in essentially energy-independent streaking delays. b, The streaking delays as a function of the solids’ permittivity at 720 nm, expressed by the field attenuation factor α = 1/ɛr. Grey areas in a and b indicate the variation of the delays with the elastic scattering time. Arrows and the shaded rectangle in b indicate the range of α parameters for typical dielectrics; the dashed horizontal line marks the value for SiO2. c, Energy-dependent IMFPs obtained in previous work6,34,35,36 (solid lines, see Supplementary Information for details). IMFP predicted by a simplified Lotz formula (dashed line). Note that the Lotz data are not shown for higher energies as the simplified model neglects lower-lying bands. IMFP from quantitative simulations of our experimental data using a scaled Lotz formula for the energy range 20–30 eV (red dots).
In summary, our joint experimental and theoretical work uncovers the physics encoded in attosecond streaking on dielectrics and resolves the characterization problem of inelastic scattering in these materials. Attosecond streaking in dielectrics differs from metals where the NIR streaking field takes effect only on the surface of the material. The presence of the field inside the dielectric determines the importance of elastic and inelastic scattering on the streaking delay. We found that for most dielectric materials the streaking delay is largely independent of the elastic scattering time thus enabling the characterization of inelastic scattering. The accessible energy range depends only on the photon energy of the attosecond pulse, which even currently covers tens of electronvolts to kiloelectronvolts and might be further extended in the future. Our approach permits characterization of inelastic scattering in a wide range of dielectric solids and liquids, including amorphous dielectrics such as water, which could be inserted in the form of droplets or as a thin jet. Direct access to IMFPs in dielectrics for a wide range of energies including the otherwise inaccessible range below 50 eV holds promise for improving our understanding of radiation damage.
Data availability.
The data that support the plots within this paper and other findings of this study are available from the corresponding authors on reasonable request.
Additional Information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
Balling, P. & Schou, J. Femtosecond-laser ablation dynamics of dielectrics: basics and applications for thin films. Rep. Prog. Phys. 76, 036502 (2013).
Krausz, F. & Stockman, M. I. Attosecond metrology: from electron capture to future signal processing. Nat. Photon. 8, 205–213 (2014).
Toburen, L. H. et al. Electron emission from amorphous solid water induced by passage of energetic protons and fluorine ions. Rad. Res. 174, 107–118 (2010).
Garrett, B. C. et al. Role of water in electron-initiated processes and radical chemistry? Issues and scientific advances. Chem. Rev. 105, 355–390 (2005).
Caleman, C. et al. Radiation damage in biological material: electronic properties and electron impact ionization in urea. Europhys. Lett. 85, 18005 (2009).
Siddharth, H. P., Vaishnav, B. G. & Joshipura, K. N. Electron inelastic mean free paths in solids: a theoretical approach. Chin. Phys. B 21, 093402 (2012).
Powell, C. J. Inelastic scattering of kilovolt electrons by solids and liquids: determination of energy losses, cross sections, and correlations with optical data. Health Phys. 13, 1265–1276 (1967).
Goldmann, M., Miguel-Sánchez, J., West, A. H. C., Yoder, B. L. & Signorell, R. Electron mean free path from angle-dependent photoelectron spectroscopy of aerosol particles. J. Chem. Phys. 142, 224304 (2015).
Itatani, J. et al. Attosecond streak camera. Phys. Rev. Lett. 88, 173903 (2002).
Cavalieri, A. L. et al. Attosecond spectroscopy in condensed matter. Nature 449, 1029–1032 (2007).
Neppl, S. et al. Attosecond time-resolved photoemission from core and valence states of magnesium. Phys. Rev. Lett. 109, 087401 (2012).
Okell, W. A. et al. Temporal broadening of attosecond photoelectron wavepackets from solid surfaces. Optica 2, 383–387 (2015).
Locher, R. et al. Energy-dependent photoemission delays from noble metal surfaces by attosecond interferometry. Optica 2, 405–410 (2015).
Borisov, A. G., Sánchez-Portal, D., Kazansky, A. K. & Echenique, P. M. Resonant and nonresonant processes in attosecond streaking from metals. Phys. Rev. B 87, 121110 (2013).
Zhang, C.-H. & Thumm, U. Attosecond photoelectron spectroscopy of metal surfaces. Phys. Rev. Lett. 102, 123601 (2009).
Kelkensberg, F., Koenderink, A. F. & Vrakking, M. J. J. Attosecond streaking in a nano-plasmonic field. New J. Phys. 14, 093034 (2012).
Li, J., Saydanzad, E. & Thumm, U. Retrieving plasmonic near-field information: a quantum-mechanical model for streaking photoelectron spectroscopy of gold nanospheres. Phys. Rev. A 94, 051401 (2016).
Prell, J. S., Borja, L. J., Neumark, D. M. & Leone, S. R. Simulation of attosecond-resolved imaging of the plasmon electric field in metallic nanoparticles. Ann. Phys. 525, 151–161 (2013).
Süßmann, F. & Kling, M. F. Attosecond nanoplasmonic streaking of localized fields near metal nanospheres. Phys. Rev. B 84, 121406(R) (2011).
Neppl, S. et al. Direct observation of electron propagation and dielectric screening on the atomic length scale. Nature 517, 342–346 (2015).
Liao, Q. & Thumm, U. Attosecond time-resolved streaked photoemission from Mg-covered W(110) surfaces. Phys. Rev. A 92, 031401 (2015).
Wilson, K. R. et al. Size-dependent angular distributions of low-energy photoelectrons emitted from NaCl nanoparticles. Nano Lett. 7, 2014–2019 (2007).
Ellis, J. L. et al. Materials properties and solvated electron dynamics of isolated nanoparticles and nanodroplets probed with ultrafast extreme ultraviolet beams. J. Phys. Chem. Lett. 7, 609–615 (2016).
Hickstein, D. D. et al. Observation and control of shock waves in individual nanoplasmas. Phys. Rev. Lett. 112, 115004 (2014).
Süßmann, F. et al. Field propagation-induced directionality of carrier-envelope phase-controlled photoemission from nanospheres. Nat. Commun. 6, 7944 (2015).
Zherebtsov, S. et al. Controlled near-field enhanced electron acceleration from dielectric nanospheres with intense few-cycle laser fields. Nat. Phys. 7, 656–662 (2011).
Signorell, R. et al. Nanofocusing, shadowing, and electron mean free path in the photoemission from aerosol droplets. Chem. Phys. Lett. 658, 1–6 (2016).
Wigner, E. P. Lower limit for the energy derivative of the scattering phase shift. Phys. Rev. 98, 145–147 (1955).
Smirnova, O., Mouritzen, A. S., Patchkovskii, S. & Ivanov, M. Y. Coulomb-laser coupling in laser-assisted photoionization and molecular tomography. J. Phys. B 40, F197 (2007).
Zhang, C. H. & Thumm, U. Electron-ion interaction effects in attosecond time-resolved photoelectron spectra. Phys. Rev. A 82, 043405 (2010).
Dahlström, J. M. et al. Theory of attosecond delays in laser-assisted photoionization. Chem. Phys. 414, 53–64 (2013).
Seiffert, L. et al. Competition of single and double rescattering in the strong-field photoemission from dielectric nanospheres. Appl. Phys. B 122, 1–9 (2016).
Kuhr, J. C. & Fitting, H. J. Monte Carlo simulation of electron emission from solids. J. Electron Spectrosc. Relat. Phenom. 105, 257–273 (1999).
Tanuma, S., Powell, C. J. & Penn, D. R. Calculations of electron inelastic mean free paths. III. Data for 15 inorganic compounds over the 50–2,000 eV range. Surf. Interface Anal. 17, 927–939 (1991).
Ashley, J. C. & Anderson, V. E. Interaction of low-energy electrons with silicon dioxide. J. Electron Spectrosc. Relat. Phenom. 24, 127–148 (1981).
Akkerman, A. et al. Inelastic electron interactions in the energy range 50 eV to 10 keV in insulators: alkali halides and metal oxides. Phys. Status Solidi b 198, 769–784 (1996).
Acknowledgements
We are grateful for support by the EU via the ERC grants ATTOCO (no. 307203), STARLIGHT (no. 637756) and ELYCHE (no. 227355), LASERLAB-EUROPE (no. 284464, EU Seventh Framework Programme), the Max Planck Society and the DFG through the Cluster of Excellence: Munich Centre for Advanced Photonics (MAP), SPP1391, SPP1840 and SFB 652/3. We acknowledge the computing time provided by the North-German super-computing center HLRN (project ID mvp00011). We acknowledge help in editing the manuscript from B. Steffl and fruitful discussions with V. S. Yakovlev, H. J. Wörner and R. Signorell.
Author information
Authors and Affiliations
Contributions
L.S., Q.L., S.Z. and A.T. contributed equally to this work. M.F.K., F.C. and T.F. conceived the measurement concept and implementation. Q.L., S.Z., A.T., M.C.C., M.G., P.R. and F.C. performed the measurements. F.S., K.W., J.S., G.S., L.P. and F.F. were involved in the set-up of the experiment and experimental infrastructure. I.H., V.M., C.G. and E.R. prepared and characterized the SiO2 nanoparticles. L.S. and T.F. developed the simulation model and performed the simulations. L.S., Q.L., S.Z., A.T., T.F., F.C. and M.F.K. evaluated, analysed and interpreted the results. All authors discussed the results and contributed to the final manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary information
Supplementary information (PDF 1836 kb)
Rights and permissions
About this article
Cite this article
Seiffert, L., Liu, Q., Zherebtsov, S. et al. Attosecond chronoscopy of electron scattering in dielectric nanoparticles. Nature Phys 13, 766–770 (2017). https://doi.org/10.1038/nphys4129
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys4129
This article is cited by
-
Attosecond metrology of the two-dimensional charge distribution in molecules
Nature Physics (2024)
-
Raman time-delay in attosecond transient absorption of strong-field created krypton vacancy
Nature Communications (2024)
-
Sub-cycle multidimensional spectroscopy of strongly correlated materials
Nature Photonics (2024)
-
Attosecond field emission
Nature (2023)
-
Lightwave electronics in condensed matter
Nature Reviews Materials (2023)