Abstract
Plasmonic antennas can enhance the intensity of a nanojoule laser pulse by localizing the electric field in their proximity1. It has been proposed that the field can become strong enough to convert the fundamental laser frequency into high-order harmonics through an extremely nonlinear interaction with gas atoms that occupy the nanoscopic volume surrounding the antennas2,3,4. However, the small number of gas atoms that can occupy this volume limits the generation of high harmonics5,6,7. Here we use an array of monopole nano-antennas to demonstrate plasmon-assisted high-harmonic generation directly from the supporting crystalline silicon substrate. The high density of the substrate compared with a gas allows macroscopic buildup of harmonic emission. Despite the sparse coverage of antennas on the surface, harmonic emission is ten times brighter than without antennas. Imaging the high-harmonic radiation will allow nanometre and attosecond measurement of the plasmonic field8 thereby enabling more sensitive plasmon sensors9 while opening a new path to extreme-ultraviolet-frequency combs10.
Similar content being viewed by others
Main
Traditional high-harmonic generation occurs in rare-gas atoms11,12. Therefore, early experiments with plasmonic antennas2 or funnels3 assumed that high harmonics were generated through local field enhancement in the gas surrounding the nanostructures. However, considerable enhancement is also achieved below and around the antennas, in the material that supports them, as demonstrated in Supplementary Fig. 1.
In recent years, high harmonics have also been generated without nanostructures directly from the bulk of a ZnO crystal13, and subsequently from various other materials14,15,16—in some cases with peak intensities as low as 1011–1012 W cm−2. These intensities are two to three orders of magnitude lower than those required in the gas phase. Not only is the threshold intensity to drive this nonlinear optical process lower than in gases, but the density of solids is ∼1,000 times greater. Hence, generating plasmon-assisted high harmonics within a crystalline substrate should overcome the limit of previous experiments (that is, the need to increase the number of emitters), and improve the longevity of the nanostructures to high-power irradiation (the longevity depends on their structural quality). These advantages have been exploited in a recent experiment conducted on Au-coated sapphire nano-cones17, where the surface plasmon is adiabatically excited—rather than resonantly excited as in this letter.
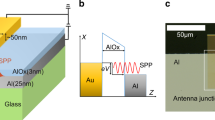
Figure 1a shows a sketch of the experimental setup (see also Supplementary Information). We focus infrared femtosecond laser pulses with a central wavelength of 2.1 μm onto an array of Au monopolar nano-antennas fabricated on a thin film of single-crystal Si (500 nm thick) grown on an Al2O3 single-crystal substrate (0.5 mm thick). Figure 1b shows a high-resolution scanning electron micrograph of the structures (design and fabrication details are reported in the Supplementary Information). Two designs are implemented, with the antennas parallel to either the [110] or the [100] orientation of the Si crystal (therefore, rotated by 45°).
a, Laser pulses with a duration of 100 fs and with a centre wavelength of 2.1 μm are focused with a CaF2 lens on an array of Au monopolar nano-antennas. The antennas are fabricated on a 500-nm-thick single-crystal Si film grown over a 500 μm sapphire substrate (M-plane cut). A combination of a half-wave plate (HWP) and a quarter-wave plate (QWP) compensates for the birefringence of the sapphire substrate to achieve horizontal linear polarization inside the Si film. b, High-resolution scanning electron micrograph of an Au nano-antenna array. The antenna major axis is aligned along the [110] direction of the Si crystal, which yields the strongest high-harmonic emission from bulk Si. The length, width and height of the monopoles determine the resonant wavelength to 2.1 μm, the fundamental laser wavelength (see Supplementary Information for details about the design).
Figure 2a shows the high-harmonic spectrum produced by antennas in the configuration parallel to the [110] Si lattice. The emission extends from the 5th to the 9th harmonic for an incident intensity (in vacuum) of 3 × 1010 W cm−2. The 11th harmonic, at 190 nm, lies beyond the detectable spectral range of our experimental setup. When the laser polarization is parallel to the antennas (red line), the high-harmonic emission is 5 to 10 times stronger than for polarization orthogonal to the antennas (green line), a configuration that does not lead to field enhancement (see Supplementary Fig. 1). In fact, in the latter case, the high-harmonic power spectrum is almost identical to that emitted from an area without any nano-antennas (black line). Parallel and perpendicular polarizations correspond to equivalent crystal directions; therefore, harmonic emission from bulk silicon is unchanged. Despite the small area covered by the antennas (8%), and the small volume over which the field is enhanced, emission from the array is stronger than the emission from the bulk, that is, off the array (black line). We estimate that the high-harmonic emission is confined to regions of ∼20 × 20 nm2 on either side of each antenna, and that the high-harmonic emission density in these regions is increased by ∼3 × 103–3 × 104 times with respect to the bulk (see Supplementary Information).
a, High-harmonic spectrum extending up to the 9th harmonic (233 nm), when antennas aligned along the [110] direction are illuminated with a polarization parallel (red line) and perpendicular (green line) to the major axis of the antennas. The black line is the emission from bulk Si, when the sample is illuminated on the unpatterned material beside the array. The detection limit of our spectrometer extends to 200 nm, which is not enough to measure the 11th harmonic (at 190 nm). The vacuum intensity of the infrared driver is 3 × 1010 W cm−2. b, The peak harmonic signal from an array of antennas with their axis parallel to the [110] direction of the Si crystal (coloured circles) and from the bulk (grey circles), for polarization parallel to the axis of the antennas, is plotted as a function of the intensity of the infrared laser. The On/Off contrast decreases with increasing laser intensity (blue arrow pointing up-right), and remains close to unity for decreasing laser intensity (blue arrow pointing down-left). The scaling of bulk harmonics is reversible (not shown). When the axis of the antennas is parallel to the [100] direction instead, harmonic emission is weaker (open diamonds with coloured edges). Bulk emission from the [100] direction (open diamonds with grey edges) is also similarly weaker than from [110], suggesting that harmonics are emitted from Si rather than from Au. All harmonics scale non-perturbatively. The dashed black line, which scales with I5, is a guide to the eye.
In Fig. 2b we show the intensity dependence of the harmonic radiation yield. Emission from antennas whose axis is parallel to the [100] direction (coloured diamonds in Fig. 2b) is weaker than for those aligned parallel to the [110] direction (coloured circles in Fig. 2b), as similarly measured for the bulk16 (compare grey circles with grey diamonds in Fig. 2b). Harmonic emission from Au would be irrespective of the orientation of the substrate. Further proof that the emission occurs from Si rather than Au is reported in Supplementary Fig. 3, which shows an image of the 5th harmonic generated from Si (bright areas) and not from micrometre-sized thin Au electrodes (black areas).
For antennas parallel to the [110] direction, all harmonics from the bulk scale approximately as I3.5, where I is the incident laser intensity, whereas perturbative nonlinear optics predicts In, where n is the harmonic order18. A slightly slower scaling, also non-perturbative, has been measured from bulk ZnO (ref. 13). All harmonic orders emitted from the array (coloured lines) show the same intensity dependence, scaling approximately with I3. This suggests that they are also generated non-perturbatively. The different scaling can arise from saturation of ionization above a threshold intensity (as found for ZnO; ref. 13): because of enhancement, emission from the array corresponds to a higher intensity inside Si, which results in slower scaling. Alternatively, it may also arise from progressive damage to the antennas, as explained below.
The contrast between ‘on’ and ‘off the array’ steadily decreases with increasing laser intensity, approaching unity at the highest intensity, and then remains close to one for decreasing laser intensity. We interpret this irreversible behaviour as being due to progressive damage, but it is unclear whether it occurs to the Si or to the antennas (the antennas do not seem to be obviously altered, see Supplementary Fig. 6). Harmonics from unpatterned Si behave reversibly. In higher-bandgap materials, the intensity required for high-harmonic generation increases, and extensive damage to the antennas is expected19,20. However, generating harmonics from the substrate, rather than from gas atoms placed near the antennas, offers opportunities to overcome the damage limit by encapsulating the antennas in a transparent dielectric medium, such as SiO2 or MgF2. Alternatively, the antennas can be buried in the Si film or fabricated with materials more resilient than Au, such as TiN (ref. 21).
The diffraction of the high-harmonic beam carries information about the spatial distribution of nanoscopic emission regions. The simulations predict an inhomogeneous field enhancement, which is strong at the ends of the antennas and all along the edges (see Supplementary Fig. 1). Although these tiny features cannot be imaged with the infrared beam (unless electrons22 or near-field probes23 are used), they should be distinguishable with a short-wavelength high-harmonic beam, whose diffraction limit of λHH/2 approaches 100 nm (λHH is the wavelength of a high harmonic order). Figure 3 shows a corner of the array imaged with a magnification of 160 taken using a lens with NA = 0.75 and the 5th harmonic (λ = 420 nm), for polarization of the driving field parallel (Fig. 3a) and perpendicular (Fig. 3b) to the axis of the antennas. The emission is clearly brighter over the array for parallel polarization—another indication of enhancement. The blurring of the sharp edge of the array can be used to estimate a resolution of ∼1.6 μm (4.6 times larger than the expected diffraction limit, defined by the Rayleigh criterion r = 0.61λ/NA). This resolution is not sufficient to resolve individual nano-antennas. A larger-numerical-aperture lens should allow individual regions of field enhancement to be imaged. Lens-less imaging can also be used to exceed the diffraction limit24,25.
Image with the 5th harmonic of a corner of an illuminated array. a, The harmonic is emitted only for the portion of the beam that overlaps with the array and for polarization parallel to the antennas’ major axis—a proof of field enhancement. b, The emission disappears for polarization perpendicular to the antennas’ major axis. At this intensity, no harmonic emission is observed from the bulk. The contour of the array is marked by the white dotted line.
Our results have a number of important implications. First, because high-harmonic emission lasts only a fraction of the optical cycle, imaging the high harmonics can map the sub-cycle dynamics of the collective electronic motion, which influence the temporal8 and spatial properties26 of the local plasmonic field. For example, if the antennas are resonant with a ‘probing field’ that excites plasma oscillations, then the resulting local field will perturb the high-harmonic generation process driven by a non-resonant driver. The perturbation will alter the spatial27 or spectral28,29 properties of the harmonic beam. By measuring the beam, we will be able to track the spatial evolution of the local field with attosecond temporal resolution.
Second, the interference between near field and bulk harmonics will contain a wealth of information about the fields in the antennas. For example, as the laser wavelength is scanned across the plasmonic resonance, the amplitude and phase of the near field will be modified relative to the bulk—which is largely unaffected by the frequency sweep. Each harmonic created in the array will inherit the phase shift of the plasmonic field, multiplied by the harmonic order. Thus, this homodyne detection scheme offers a highly sensitive method for studying plasmon responses that differs from previously proposed methods26, where an electron microscope images electrons that are simultaneously photoionized by attosecond pulses and accelerated in the local field of an infrared pulse. Coherent detection of high harmonics will enable a new generation of plasmon sensors of unprecedented sensitivity, in which small phase shifts of the resonance herald tiny variations in the environment surrounding the antennas.
Third, an inhomogeneous field will accelerate electron–hole pairs differently throughout the volume and even between successive laser half-cycles, since the electrons and holes follow oppositely directed paths. If the variation in the field is sufficient across the path length of the electron and the hole, the inversion symmetry is broken, allowing even harmonics30 to be produced. In fact, high harmonics can be thought of as a quantum sensor for weak fields or for field inhomogeneity. We do not observe emission of even harmonics. As discussed in the Supplementary Information, the opposite field gradients at the two ends of each antenna average the even harmonic signal in the far field to zero, and the asymmetry on either side of the antennas is predicted to be too small to yield appreciable even harmonic emission. The spatial average would be removed by imaging single nano-antennas with a sufficiently high NA lens, or by designing asymmetric antennas. In addition, the effect of the anisotropic field will be enhanced with a longer wavelength driver. We predict that at 3.7 μm the even harmonic signal from the dominant short-trajectory electron–hole pairs will reach ∼3% of the nearest odd harmonic.
To conclude, we have observed non-perturbative harmonic generation from crystalline bulk Si assisted by plasmonic field enhancement from an array of monopole nano-antennas. Using solids overcomes the difficulty of generating macroscopic emission with low-density gas—a scheme that was tried in previous experiments2,3,4. Harmonic emission is sensitive to the orientation of the incident linear laser polarization with respect to the major axis of the antennas. This effect can be exploited to engineer the polarization of the harmonic beam in the near field. For example, circularly polarized harmonics could be obtained by illuminating with a circularly polarized driver two overlapping arrays of antennas, with their major axis perpendicular to one another. Each antenna array will couple to the component of the electric field that aligns with the antenna’s major axis, therefore with a quarter-cycle delay between the two arrays. This delay is inherited by the harmonics (multiplied by their order). Overlapping the emission from the two arrays will result in circularly polarized odd-order harmonics. Complicated geometries, such as metasurfaces31, will allow even more precise control of many properties of high-harmonic beams, such as amplitude and orbital angular momentum.
Looking forward, light can be confined to volumes smaller than a few cubic nanometres32. In this regime, the atomic arrangement of the atoms of the antenna becomes relevant. Such tight confinement provides an opportunity to control strong-field excitation at the level of a single unit cell. This will be a valuable tool to address several conceptual issues in high-harmonic generation from solids, such as the role played by the relative diffusion of the electron and the hole, the plausibility of collisions between neighbouring electrons and holes, and the effect of boundaries and impurities on propagating electron–hole pairs. Combining solid-state technology with strong-field physics, high-harmonic generation can be engineered at will.
Methods
Fabrication of the antennas.
Several square monopole arrays were fabricated by electron-beam lithography, metal evaporation and lift-off on the (001) surface of a 500-nm-thick single-crystal silicon film (http://www.mtixtl.com/sossilicononsapphire-2.aspx). The silicon was grown on an R-plane 500-nm-thick sapphire substrate. The Si/sapphire substrate was first annealed at a temperature of 200 °C in ambient conditions for two hours. Immediately after cool down, two layers of polymethyl methacrylate (PMMA), each with a thickness of 40 nm, were spun on the substrate to produce a re-entrant electron-beam resist bi-layer. PMMA 495 A2 and 950 A2 were used for the first and second layer, respectively. Both layers were baked at 180 °C for one hour and cooled to room temperature before any further processing. The nano-antennas were patterned by electron-beam lithography at 30 keV followed by a one-hour bake at 95 °C. The samples were developed in MIBK/IPA 1:3 at 20 °C. A 2-Å-thick chromium adhesion layer was deposited directly on the substrate followed by evaporation of 200 Å of gold, both using electron-beam evaporation. The metal lift-off took place in an acetone bath at 40 °C, which was sonicated at 30 kHz for approximately one minute. Figure 1 shows a scanning electron micrograph of a nano-antenna array.
Generation and detection of high harmonics.
An optical parametric amplifier (Light Conversion OPA TOPAS-Prime) is pumped with a titanium sapphire femtosecond regenerative amplifier (Coherent Legend Elite Cryo) and delivers infrared laser pulses of 100 fs duration with a central wavelength of 2.1 μm at 10 kHz repetition rate. The beam is spatially filtered with a diamond pinhole of 150 μm diameter and refocused into the silicon sample with a magnification of 2/3. The beam waist on the sample is comparable to the size of a nano-antenna array (100 μm). The average power of the laser system is significantly attenuated from P = 150 mW to the required values of <1 mW (<100 nJ per pulse) by a combination of a spatial filter and a small aperture placed before the filter. Control over the power is achieved by slightly varying the aperture size. The waist on the sample is unaffected since it is a fixed fraction of the pinhole size.
Harmonics with photon energies above the direct bandgap of Si (at 3.4 eV) are strongly absorbed. Because the region of field enhancement extends only a few nanometres below the Si surface, to detect these harmonics the Si film must face the detector. The projection of the sapphire c axis on the surface aligns to the (100) direction of the Si crystal, and therefore shows birefringence for the desired output polarization parallel to the (110) direction. We used a combination of a half-wave and a quarter-wave plate to ensure that the polarization exiting the sapphire substrate and entering the Si film is linear and aligned along the (110) direction.
The harmonics are detected by focusing them through the slit of a visible–ultraviolet spectrometer from Ocean Optics (model USB2000+).
Data availability.
The data that support the plots within this paper and other findings of this study are available from the corresponding author on reasonable request.
Additional Information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
Stockman, M. I. Nanoplasmonics: the physics behind the applications. Phys. Today 64, 39–44 (February, 2011).
Kim, S. et al. High-harmonic generation by resonant plasmon field enhancement. Nature 453, 757–760 (2008).
Park, I.-Y. et al. Plasmonic generation of ultrashort extreme-ultraviolet light pulses. Nat. Photon. 5, 677–681 (2011).
Park, I.-Y. et al. Generation of EUV radiation by plasmonic field enhancement using nano-structured bowties and funnel-waveguides. Ann. Phys. (Leipz.) 525, 87–96 (2013).
Sivis, M. et al. Nanostructure-enhanced atomic line emission. Nature 485, E1–E3 (2012).
Sivis, M. et al. Extreme-ultraviolet light generation in plasmonic nanostructures. Nat. Phys. 9, 304–309 (2013).
Raschke, M. B. High-harmonic generation with plasmonics: feasible or unphysical? Ann. Phys. (Leipz.) 525, A40–A42 (2013).
Feist, J., Homer Reid, M. T. & Kling, M. F. Nanoplasmonic near-field synthesis. Phys. Rev. A 87, 033816 (2013).
Stewart, M. E. et al. Nanostructured plasmonic sensors. Chem. Rev. 108, 494–521 (2008).
Cingöz, A. et al. Direct frequency comb spectroscopy in the extreme ultraviolet. Nature 482, 68–71 (2012).
Li, X. F. et al. Multiple-harmonic generation in rare gases at high laser intensity. Phys. Rev. A 39, 5751–5761 (1989).
Pfeifer, T., Spielmann, C. & Gerber, G. Femtosecond x-ray science. Rep. Prog. Phys. 69, 443–505 (2006).
Ghimire, S. et al. Observation of high-order harmonic generation in a bulk crystal. Nat. Phys. 7, 138–141 (2011).
Schubert, O. et al. Sub-cycle control of terahertz high-harmonic generation by dynamical Bloch oscillations. Nat. Photon. 8, 119–123 (2014).
Luu, T. T. et al. Extreme ultraviolet high-harmonic spectroscopy of solids. Nature 521, 498–502 (2015).
Vampa, G. et al. Generation of high harmonics from silicon. Preprint at http://arXiv.org/abs/1605.06345 (2016).
Han, S. et al. High-harmonic generation by field enhanced femtosecond pulses in metal-sapphire nanostructure. Nat. Commun 7, 13105 (2016).
Boyd, R. W. Nonlinear Optics (Academic, 2003).
Pfullmann, N. et al. Bow-tie nano-antenna assisted generation of extreme ultraviolet radiation. New J. Phys. 15, 093027 (2013).
Pfullmann, N. et al. Nano-antenna-assisted harmonic generation. Appl. Phys. B 113, 75–79 (2013).
Guler, U., Shalaev, V. M. & Boltasseva, A. Nanoparticle plasmonics: going practical with transition metal nitrides. Mater. Today 18, 227–237 (April, 2015).
Barwick, B., Flannigan, D. J. & Zewail, A. H. Photon-induced near-field electron microscopy. Nature 462, 902–906 (2009).
Kawata, S., Inouye, Y. & Verma, P. Plasmonics for near-field nano-imaging and superlensing. Nat. Photon. 3, 388–394 (2009).
Zhang, B. et al. High contrast 3D imaging of surfaces near the wavelength limit using tabletop EUV ptychography. Ultramicroscopy 158, 98–104 (2015).
Chapman, H. N. et al. Femtosecond diffractive imaging with a soft-X-ray free-electron laser. Nat. Phys. 2, 839–843 (2006).
Förg, B. et al. Attosecond nanoscale near-field sampling. Nat. Commun. 7, 11717 (2016).
Kim, K. T. et al. Petahertz optical oscilloscope. Nat. Photon. 7, 958–962 (2013).
Dudovich, N. et al. Measuring and controlling the birth of attosecond XUV pulses. Nat. Phys. 2, 781–786 (2006).
Vampa, G. et al. Linking high harmonics from gases and solids. Nature 522, 462–464 (2015).
Ciappina, M. F. et al. High-order-harmonic generation from inhomogeneous fields. Phys. Rev. A 85, 033828 (2012).
Yu, N. & Capasso, F. Flat optics with designer metasurfaces. Nat. Mater. 13, 139–150 (2014).
Barbry, M. et al. Atomistic near-field nanoplasmonics: reaching atomic-scale resolution in nanooptics. Nano Lett. 15, 3410–3419 (2015).
Acknowledgements
We thank D. Crane and B. Avery for technical support. G.V. thanks M. Sivis for insightful discussions. This material is based on work supported by the Air Force Office of Scientific Research under award number FA9550-16-1-0109 and the AFOSR MURI grant number FA9550-15-1-0037. The authors also acknowledge financial support from the NRC, NSERC and CFI/ORF.
Author information
Authors and Affiliations
Contributions
G.V. and P.B.C. conceived the experiment; G.V. and T.J.H. performed the high-harmonic measurements; B.G.G. and S.S.M. designed the nano-antennas; B.G.G., A.O. and E.L.-S. fabricated the antennas; A.S. and A.Y.N. maintained the laser source; D.M.V., P.B.C. and P.B. supervised the experiment; all authors contributed to the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary information
Supplementary information (PDF 615 kb)
Rights and permissions
About this article
Cite this article
Vampa, G., Ghamsari, B., Siadat Mousavi, S. et al. Plasmon-enhanced high-harmonic generation from silicon. Nature Phys 13, 659–662 (2017). https://doi.org/10.1038/nphys4087
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys4087
This article is cited by
-
Sub-cycle multidimensional spectroscopy of strongly correlated materials
Nature Photonics (2024)
-
Lightwave electronics in condensed matter
Nature Reviews Materials (2023)
-
Carrier-envelope phase on-chip scanner and control of laser beams
Nature Communications (2023)
-
High-harmonic generation in CdTe with ultra-low pump intensity and high photon flux
Communications Physics (2023)
-
Role of Van Hove singularities and effective mass anisotropy in polarization-resolved high harmonic spectroscopy of silicon
Communications Physics (2022)