Intrinsic photonic wave localization in a three-dimensional icosahedral quasicrystal

Abstract

Wave transport is one of the most interesting topics related to quasicrystals. This is due to the fact that the translational symmetry strongly governs the transport properties of every form of wave. Although quasiperiodic structures with^1,2,3,4 or without^1,5,6,7 disorder have been studied, a clear mechanism for wave transport in three-dimensional quasicrystals including localization is missing^8,9. To study the intrinsic quasiperiodic effects on wave transport, the time invariance of the lattice structure and the loss-free condition must be controlled^10,11. Here, using finite-difference methods, we study the diffusive-like transport and localization of photonic waves in a three-dimensional icosahedral quasicrystal without additional disorder. This result appears at odds with the well-known theory¹² of wave localization (Anderson localization), but we found that in quasicrystals the short mean free path of the photonic waves makes localization possible.

Main

The first discovery of a quasicrystal¹³ disproved the long-standing conjecture in condensed matter physics that only crystalline materials with translational symmetry could be densely packed and highly ordered. In crystalline materials the waves with wavelengths commensurate with the crystal’s periodicity can transmit without scattering loss, leading to ballistic transmission. Disordered materials can be contrasted with ordinary crystals. Because of frequent scattering, wave transport in disordered materials is usually described by random walks leading to diffusive transmission, for example, Ohm’s law¹⁴. Considering the wave nature of electrons, Anderson predicted that if the degree of structural randomness is sufficiently large, the wave interference will result in complete halting of electrons, the so-called Anderson localization¹⁵, and the transmission coefficient will decrease exponentially with increasing sample thickness¹⁶. Because of the mixed structural characteristics—for example, the lack of translational symmetry of the disordered media and the highly ordered structure of the ordinary crystals—a critical question has been raised regarding wave transport in quasicrystals, including localization, which has not been thoroughly answered¹⁷.

To the best of our knowledge, this is the first demonstration of the intrinsic localization of photonic waves in a three-dimensional (3D) quasicrystal without additional disorder. Photonic wave localization in a 3D icosahedral quasicrystal is carefully investigated by photonic wave transmission utilizing finite-difference methods. The diffusive transport and localization of photonic waves in the quasicrystal are revealed by widely accepted approaches^18,19. We characterize the localization phenomena by analysing the spatial and temporal evolution of photonic waves. The localization mechanism is elucidated using the photonic band structures of quasicrystal approximants.

An icosahedral quasicrystal structure can be built according to the substitution rules²⁰ as shown in Fig. 1a–i and further detailed in Supplementary Figs 1–5. The rhombic triacontahedron, indicated in purple in Fig. 1a, constitutes a large proportion of an icosahedral quasicrystal. Rhombic triacontahedrons are derived from the intersection of five cubes (Fig. 1j)²¹. The parallelogram shape planes of the rhombic triacontahedrons can be placed on the three faces of the five cubes. The planes derived from the parallelograms are expected to form effective Brillouin zone faces and give rise to Bragg scattering.

Figure 1: Schematic of the construction of 3D icosahedral quasicrystals and the expected planes giving rise to multiple Bragg scattering.

a–i, Substitution rules for constructing a 3D icosahedral quasicrystal²⁰. a, A triacontahedron represented in purple is located at the centre of the icosahedral quasicrystal. b, Thirty rhombic dodecahedra represented in green are placed on the two-fold axes. c, Twenty rhombohedra represented in orange are placed on the three-fold axes, and twelve clusters of ten rhombohedra are placed on the five-fold axes. d, Thirty triacontahedra are placed on the two-fold axes, and twelve rhombic icosahedra represented in blue are placed on the five-fold axes. e, Twenty clusters of ten rhombohedra are placed on the three-fold axes. f, Twelve clusters of five rhombic icosahedra on the five-fold axes are capped by twelve clusters of ten rhombohedra. g, Twelve clusters of five rhombic dodecahedra are placed on the five-fold axes, and twelve rhombic icosahedra are placed in the middle of each edge of the inflated cell. h, Twenty clusters of ten rhombohedra are placed on the three-fold axes. i, Finally, twenty clusters of three rhombic icosahedra are placed on the three-fold axes, and thirty triacontahedra are placed on the two-fold axes. j, The rhombic triacontahedron, the most populated polyhedron, can be derived from the intersection of five cubes whose faces have indices: {100}, {τ11/τ}, , {11/ττ}, , where is the golden mean²¹. k, A plane that leads to multiple Bragg scattering is shown. The rod length, d, can be arbitrarily chosen since the dielectric constants of the constituting materials are assumed to be independent of frequency. In the present work, d is set to 1 cm and the optical responses are obtained at around 15 GHz.

Transmission spectra are obtained using a finite-difference time-domain code²². A diamond structure is also compared as a reference. The photonic bandgap of the diamond on the first Brillouin zone boundary overlaps nicely with the low-intensity spectral regime (Fig. 2e). Thus, low-transmission footprints originate from the photonic bandgap²³. Similar low-transmission footprints are found in the quasicrystal (Fig. 2c), exhibiting good agreement with the Bragg scattering from the effective Brillouin zone faces with a plane distance of 0.85d, where d is the rod length of the rhombic triacontahedron (Fig. 1k). On the basis of interpretation of the diamond structure, we suggest that photonic bandgaps are formed on the effective Brillouin zone faces. However, the bandgap is very narrow and loosely defined thus exhibiting characteristics of pseudogaps¹⁶. Indeed, a previous study³ demonstrated that a quasicrystal has pseudogaps. Since localized states can exist in the pseudogap regime¹⁶, the wave localization is expected to occur in the low-intensity spectral regime of the quasicrystal.

Figure 2: Calculated transmission spectra of a 3D icosahedral quasicrystal and a diamond structure.

a, Schematic of the incident beam and detector arrangement for the transmission spectra calculations. b, The quasicrystal structure for the transmission calculation. c, Transmission intensity as a function of the rotation angle about a two-fold rotation axis of the quasicrystal and the scaled frequency, ωd/2πc, where c is the speed of light. The dashed curves in c are Bragg scattering lines from the effective Brillouin zone faces with plane distance 0.85d in the quasicrystal. Colours indicate the zone faces of the five cubes constituting a rhombic triacontahedron (Fig. 1j), where the effective Brillouin zone faces and their predicted scattering lines are detailed in Supplementary Fig. 8. d, The diamond structure for the transmission calculation. e, Transmission intensity as a function of the rotation angle and the scaled frequency ωd/2πc. The diamond structure is rotated to coincide with the high-symmetry points on the first Brillouin zone boundary represented as yellow in d. The grey dashed lines in e are the calculated photonic bands on the first Brillouin zone boundary. f,g, Time-dependent transmitted intensity for the quasicrystal (f) and the diamond structure (g). Photonic waves with three different scaled frequencies of 0.558, 0.671 and 0.906 transmitted for the 30°, 45° and 90° rotations of the quasicrystal. The waves at the frequencies 0.455 and 0.586 transmit for the 0° and 90° rotations of the diamond. All of the points are marked on the transmission spectra. As reference, the dashed line in cyan shows the long-term behaviour predicted by the diffusion theory, e^{−(π2D/L2)t}, where D is the diffusion coefficient, L is the sample thickness, and t is the time²⁴. The fit to the theory gives D = 0.01034 cm² ps⁻¹, where L = 17.5 cm.

Based on the transmission spectra time-dependent transmission profiles in the low-transmission regime are calculated. In the case of the quasicrystal for 30° rotation (five-fold symmetry axis), the average transmitted intensity decays exponentially during longer periods of time than 45° and 90° rotation cases, followed by a delayed decay (Fig. 2f). The time-dependent intensity profiles for 45° and 90° rotations exhibit more noticeable delays. This delay originates from wave localization because localized waves have longer lifetimes in the structure²⁴. Wave propagation along a lower-symmetry axis experiences significant delay in time-dependent transmission (comparing the 45° and 90° rotation cases). The localization is dependent on the wave-propagation direction in the quasicrystal, and lower-symmetry directions favour localization. Figure 2g shows that the transmission intensities in the diamond decrease much more quickly than those in the quasicrystal, clearly indicating ballistic propagation²⁵.

The average intensity distribution of the quasicrystal shows its lattice structure and the diffraction peaks that are irrelevant to the structure (Fig. 3a). The logarithm of the intensity cross-section reveals two aspects of transport characteristics in the quasicrystal. An average intensity profile close to the Gaussian shape corresponds to diffusive transport²⁶, while an exponential curve indicates the localization. The 30° rotation case is very similar to the Gaussian shape indicating the diffusive-like transport. The 90° and 45° cases, corresponding to the lower-symmetry axes, deviate from the Gaussian shape and exhibit sharper linear curves implying stronger localization, where the fit to the exponential function yields shorter localization lengths (Fig. 3a and Supplementary Table 2)²⁶. The intensity profile for the diamond structure is quite distinct from those of the quasicrystal (Fig. 3b). A wide range of the profile for the diamond exhibits periodic spike patterns that reflect the lattice structure due to its ballistic transport.

Figure 3: Photonic wave intensity distribution of the quasicrystal and the diamond.

a,b, Intensity distribution at the output face of the icosahedral (a) and diamond structures (b) for photonic waves at 0.905 ωd/2πc for 30°, 45° and 90° rotations, where the initial beam width is 2.0 cm. The white lines show the average logarithmic intensities of the cross-section. The dotted black lines correspond to the diffusive contribution, I ∝ exp(−2r²/σ²), and the dashed red lines represent the localization contribution, I ∝ exp(−2r/ξ), where r is the distance from the centre of the beam, σ is the Gaussian beam width, and ξ is the localization length. The shortest ξ is obtained for the 45° rotation, indicating the strongest localization²⁶. c, The beam-width changes as a function of the propagation distance in the quasicrystal and the diamond. The effective beam width is given by W_eff(L) = 〈P(L)〉^−1/2, where P(L) = [∫ I(x, y, L)²dxdy]/[I(x, y, L)dxdy]² is the inverse participation ratio, I is the intensity, and L is the propagation distance^3,26. The cyan dashed lines are the fit curves for the exponent, p, of the expanding beam given by W_eff ∼ z^p. d–f, Logarithm of the azimuthally averaged intensity, log |I|², as a function of z at the 30° (d) and 45° rotations (e) of the quasicrystal and at the 0° rotation of the diamond (f). Red arrows show wave propagation direction. The speckle patterns, log |I(x, y)|²/〈log |I|²〉, are superimposed at the bottom for all cases.

We further calculate the effective beam width. The beam-width changes as a function of propagation distance quantitatively show the confinement of the propagating waves (Fig. 3c). For the diamond structure, the beam width grows rapidly up to approximately L = 4 cm due to the radiation from the beam centre and then increases slowly. As the distance increases, the propagating eigenstates²⁷ exclusively allow electromagnetic waves to travel through the diamond, where the speckle pattern of Fig. 3f shows the eigenstates. The exponents of the width variation are approximately 1.05 for 0° rotation and 0.89 for 90° rotation. A value close to 1.0 indicates ballistic transport^3,26. The beam width change of the quasicrystal is substantially different from that of the diamond. The beam width increases slowly indicating stronger confinement, and the slope of the curve smoothly changes. The calculated exponents for 30°, 45° and 90° are close to 0.5, indicating that wave propagation in the quasicrystal is diffusive-like^3,26.

Similar behaviour is observed in the azimuthally averaged intensities as a function of the propagation distance (Fig. 3d–f). The initial intensity profile for the quasicrystal is close to the Gaussian distribution, whereas in the middle of the propagation, a pronounced peak near the beam centre position appears exhibiting localized waves in the quasicrystal (Fig. 3d, e). The final intensity profile for the 30° rotation is more similar to the Gaussian profile than that of the 45° rotation, indicating more diffusive transport. Propagation along the low-symmetry axis exhibits a more localized distribution and larger deviations from the Gaussian profile. These results agree with those from the time-dependent profiles. For the diamond structure, the shape with periodic spike patterns is invariant and broad (Fig. 3f).

A well-known criterion for Anderson localization in disordered materials is the Ioffe–Regel condition¹², kl^∗ ≤ 1, where k is a wavevector, and l^∗ is the transport mean free path. The calculated mean free paths in the quasicrystal are very small, and kl^∗ is close to 5 at frequencies of 0.558 and 0.906, where the localization occurs (Table 1 and Fig. 4a). The low kl^∗ for the 45° rotation implies a better probability of localization. A recent experimental study²⁸ demonstrated 3D Anderson localization under a similar condition (kl^∗ < 5). At the low frequency, 0.453, the kl^∗ values exceed 5 and photonic wave localization is weakened. The mean free path shortens as the frequency increases, and localization is favoured at higher frequencies. Therefore, the main driving force of localization in the quasicrystal is the short mean free path.

Table 1 The calculated k and mean free path, l, of the quasicrystal and diamond structures at four different frequencies.

Figure 4: Mean free path versus kl and photonic band structure of a 1/1 approximant unit cell of a 3D icosahedra quasicrystal.

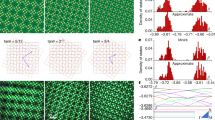
a, Plots of the mean free path versus kl for the quasicrystal and the diamond at three different frequencies. The transport mean free path, l^∗, of the quasicrystal and the scattering mean free path, l_s, of the diamond are used. b, A 1/1 approximant unit cell is prepared by cutting off the quasicrystal with a cubic supercell, where the number of the rhombic triacontahedra in the supercell is 1. c, The stereoprojection of an icosahedron is represented in grey, and that of a cube is shown in blue. The polygons on the stereoprojection indicate the order of rotational symmetry. The symmetry point R in the approximant is consistent with the three-fold symmetry points of the icosahedral structure. Similarly, the symmetry point X corresponds to two-fold symmetry points, and the symmetry point M, which is located between the three-fold and five-fold symmetry points, is irrelevant to all symmetry points. d, Photonic band structure of a 1/1 approximant unit cell. The orange dotted lines show the structure-free bands, obtained from an empty cube without any structures. The structure-free bands are scaled with a slower light velocity utilizing the effective medium approach, , where V_f is the volume fraction of the unit cell and ɛ_r is the dielectric constant of the material. e, Magnified view of the photonic band structure for the supercell with different frequency range. f, Photonic band structures for the supercell from the Γ point to the three different symmetry points, X, M and R.

Photonic band structures of the 1/1 approximant unit cell are studied to understand the mean free path variation in the quasicrystal. For comparison, the band structures of an empty cubic unit cell, that is, the structure-free bands, are overlapped to separate artefacts from the supercell. The structure-free bands indicate photonic wave propagation in a homogeneous medium. Two important features can be observed in the band structures: convergence of the quasicrystal photonic bands to the structure-free bands at low frequencies (lower part of Fig. 4e) and band flattening at high frequencies (upper part of Fig. 4e). Larger band flattening corresponds to slower group velocity and more scattering events. Thus, increased scattering events at high frequencies cause decreasing scattering mean free path²⁹ and increase the possibility of wave localization in light of the Ioffe–Regal condition.

The degree of band flattening in the approximant changes with varying the wavevector direction and is highly related to the quasicrystal symmetry. To investigate symmetry relationships between the approximant and the quasicrystal, we superimpose the stereoprojection of the approximant unit cell on the icosahedral structure (Fig. 4c). We examine the band flattening from the Γ point to the three points (Fig. 4f). The band flattening phenomena become more significant at lower-symmetry points, and the wave transmission in the low-symmetry direction is suppressed, leading to stronger localization. Similar behaviours are further observed in the 2/1 approximant unit cell (Supplementary Fig. 15).

Our results indicate the universal features of wave transport in 3D quasicrystals, including electron and phonon, and should stimulate future research on the transport properties of quasicrystalline materials. In contrast to disordered materials, quasicrystalline structures can be precisely engineered to enable the control of wave localization for future photonic applications, such as lasers.

Methods

Preparation of a 3D icosahedral quasicrystal and a diamond.

To simulate the transmission measurement, an icosahedral quasicrystal and a diamond are prepared with vertices connected by rods of length d = 1 cm. The rod diameters are 0.3 cm and 0.4 cm for the quasicrystal and diamond, respectively. The volume fraction of the quasicrystal is about 0.17, and that of the diamond is 0.283.

Finite-difference grid generation.

The 3D structures are converted into finite-difference grids utilizing a freely available code (contact A. H. Aitkenhead (adam.aitkenhead@christie.nhs.uk)) that reads and voxelizes a 3D triangular-polygon mesh in stereolithography (STL) file format. The voxelized result is given in finite-difference grids that can be imported into finite-difference time-domain (FDTD) simulation packages.

Finite-difference time-domain simulation.

The numerical simulations of the transmission and intensity field distribution are performed using MIT Electromagnetic Equation Propagation (MEEP)²², which is freely available code based on the FDTD method. The constituting material for the structures is assumed to be a loss-free polymeric material with the dielectric constant of 2.72. The value of vacuum is 1. As Maxwell’s equations are scale invariant, all of the simulation units can be conveniently chosen depending on the rod length d, where the length and time units are proportional to d, but the frequency unit is inversely proportional to d. For example, the frequency ωd/2πc = 1 corresponds to 30 GHz in the case of d = 1 cm. The number of pixels per distance unit in all simulations is set to 20 pixels cm⁻¹ and the overall system size including the perfectly matched layer (PML) reaches 25 × 25 × 25 cm. The PML layer thickness is given by larger than twice the largest wavelength to avoid electromagnetic wave reflections on the interface of vacuum and the PML layer.

The transmission intensities are obtained by rotating the structures along the two-fold rotational symmetry axis by 5° as shown in Fig. 2a. A Gaussian-pulse source with the temporal width 60 ps is applied to investigate time-dependent transmission intensities. The average intensity distributions are obtained after electromagnetic fields in a system are saturated with a plane-wave source. Further detailed simulation set-up and implementation using MEEP are given in Supplementary Information.

Finite-difference frequency-domain simulation.

We developed a finite-difference frequency-domain simulator utilizing parallel Arnoldi Package (ARPACK)³⁰ to efficiently calculate the photonic band structures. The governing equation for the frequency-domain Maxwell equation is

where ɛ is the relative permittivity, H is the magnetic fields, ω is the angular frequency, and c is the speed of light. ɛ is set to 2.72 for structures and 1 for vacuum; the same as those of the FDTD simulation. The computational implementation is further detailed in the Supplementary Information.

The mean free path calculation.

To calculate the transport mean free path, l^∗, for diffusive wave transport and the scattering mean free path, l_s, for ballistic wave transport, a diffusion theory formalism^31,32 is used. The transmission intensities as a function of propagation distance are obtained after electromagnetic fields in a system are saturated with a plane-wave source. The absolute transmission values are obtained at multiple positions (Supplementary Fig. 13a). The calculated transmission intensities, T, are fitted using the following equation.

and

where l^∗ is the transport mean free path, l_s is the scattering mean free path, L is the sample thickness (the position of the detector), and τ_a is the absorption time indicating the time deviating from the diffusion theory in the time-resolved intensity profile, R is the wall boundary reflectivity, z₀ is the extrapolation length defined as z₀ = (2/3)l^∗(1 + R)/(1 − R), and D is the diffusion constant. The first term in equation (1) is the diffusive transport contribution, and the second term is the ballistic transport contribution.

In the present work, we assume that internal reflection is negligible following previous work³³, since the dielectric constant of the constituting material is small. Thus, z₀ is set to 0.667. The diffusion constant is 8.43 × 10⁻³ cm² ps⁻¹ as obtained from the time-resolved transmission simulation. l^∗, l_s and τ_a are used as fitting parameters. In particular, τ_a values are consistent with those of the time deviating from the diffusion theory in Fig. 2f, g and Supplementary Fig. 9.

Data availability.

The data that support the plots within this paper and other findings of this study are available from the corresponding author on request.