Abstract
Anisotropy is a fundamental property of particle interactions. It occupies a central role in cold and ultracold molecular processes, where orientation-dependent long-range forces have been studied in ultracold polar molecule collisions1,2. In the cold collisions regime, quantization of the intermolecular degrees of freedom leads to quantum scattering resonances. Although these states have been shown to be sensitive to details of the interaction potential3,4,5,6,7,8, the effect of anisotropy on quantum resonances has so far eluded experimental observation. Here, we directly measure the anisotropy in atom–molecule interactions via quantum resonances by changing the quantum state of the internal molecular rotor. We observe that a quantum scattering resonance at a collision energy of kB × 270 mK appears in the Penning ionization of molecular hydrogen with metastable helium only if the molecule is rotationally excited. We use state-of-the-art ab initio theory to show that control over the rotational state effectively switches the anisotropy on or off, disentangling the isotropic and anisotropic parts of the interaction.
Similar content being viewed by others
Main
Anisotropy leaves fingerprints on many atomic and molecular processes, but its contribution is difficult to evaluate and quantify at high energies due to the many quantum states needed to describe the process. For example, the effects of anisotropy can be traced to changes in the angular distribution of products in collisions and half-collisions that are detected with advanced ion imaging techniques9. Numerous experiments have reported orientation effects including the study of bimolecular processes such as the reactive scattering of H + D2 (ref. 10), and F + CD4 (ref. 11) as well as the inelastic scattering of NO by Ar (ref. 12). Spectroscopic techniques have been successfully used to identify hindered H2 rotation in an anisotropic potential of van der Waals molecules such as H2O + H2 and H2HF complexes13,14.
In cold and ultracold molecular processes, where the number of accessible quantum states is greatly reduced, anisotropy effects have so far been studied only in fast reactions. It has been shown that the orientation of the long-range dipole–dipole interaction between molecules can be tuned via external electric fields15. In KRb molecules this method enabled the observation of rethermalization1 and the suppression of a bimolecular chemical reaction2. In addition, the reaction of N2+ + Rb has been shown to be dominated by the anisotropic charge–quadrupole long-range interaction16. Similarly, fast Penning ionization reactions have been studied, demonstrating that the rotational state of a molecule defines the type and strength of the effective long-range interaction17. These fast processes are fully described by the long-range interactions alone. At short internuclear separations the Penning ionization occurs with unit probability, acting as a perfect absorber and preventing the formation of outgoing waves. In such a case there is no quantization along the internuclear coordinate that precludes the appearance of quantum scattering resonances.
Experiments that are capable of resolving quantum resonance states allow for collision studies with near spectroscopic precision. For example, isotope shifts have been observed in the Penning ionization of molecular hydrogen isotopologues6. Similar effects between isotopes were observed in rotational state-to-state cross-sections and linked to quantum scattering resonances appearing at different energies18. Feshbach resonances in ultracold anisotropic atom–atom collisions allowed the emergence of chaotic scattering in ultracold Er and Dy to be observed19.
The emergence of discrete quantized metastable states formed during a cold collision provides a new way to study anisotropy. Instead of recording the angular distribution of the collision products, one can conveniently alter the way anisotropy contributes by choosing different rotational quantum states of the interacting molecules. The sensitivity of the orbiting resonances to the molecular degrees of freedom has been theoretically predicted for the reaction D + H2 (ref. 20), the reactive scattering of F + H2 (ref. 21) and inelastic collisions of CO + H2 (ref. 22), for example. This effect has so far eluded experimental investigation due to the insufficient resolution of individual quantum resonance states22. The introduction of merged beam experiments that can reach temperatures as low as 10 mK (refs 3,6) allows for both low enough collision energies and sufficiently high resolutions due to the correlation that develops during the free propagation of a supersonic molecular beam23. This merged beam configuration is used in the current collision measurements, as described in the Methods.
Here we demonstrate the dramatic effect of anisotropy on shape resonances in cold Penning ionization reactions of metastable helium in the 23S1 state (He∗) with molecular hydrogen in the rotational ground and first excited states (Fig. 1). In the classical collision regime down to temperatures of several kelvin, H2 behaves similarly, independent of whether it is in the j = 0 or j = 1 internal rotational state. However, below one Kelvin we observe a striking difference. While a strong shape resonance exists for j = 1 at a collision energy of kB × 270 ± 20 mK, where kB is the Boltzmann constant, no resonances are observed in this energy range in the case of j = 0. Using state-of-the-art ab initio theory and coupled-channel quantum molecular dynamics we find that the interaction between hydrogen, which is internally in the ground rotational state, and metastable helium is effectively isotropic. This holds for any collision where the interaction anisotropy is small compared with the rotational constant of the molecule. In such a case, the anisotropic part of the interaction potential becomes important only for molecules in an excited rotational state. The wavefunction of rotationally excited H2 molecules is not spherically symmetric, which causes the anisotropic components of the interaction to come into play, whereas in the rotational ground state, where the wavefunction is spherically symmetric, the contribution of anisotropic components is zero. We show that by accurately measuring the orbiting resonance positions we can independently probe the isotropic and anisotropic parts of the interaction. As the resonance wavefunctions span both the short- and the long-range parts of the potentials, we are able to benchmark first-principles quantum dynamics calculations to within 7 × 10−3 cm−1 or 200 MHz precision. This allows for a rigorous comparison with theory and a quantitative evaluation of the different levels of treating electron correlations in electronic structure calculations.
The experimental rate coefficient is shown by the black dots as a function of the mean collision energy in units of temperature. The upper (lower) panel corresponds to H2 internally in the j = 0 (j = 1) rotational quantum state. Two shape resonances are observed below 5 K for the reaction with ortho-H2 (j = 1) at 2.37 ± 0.09 K and at 270 ± 20 mK. The j = 1 lower-energy resonance state corresponds asymptotically to the partial wave l = 3, whereas the second resonance, which appears both for j = 0 and j = 1, corresponds asymptotically to the l = 4 partial wave. In the reaction with para-H2 (j = 0), the l = 3 resonance is absent, whereas the difference in energy of the l = 4 resonance cannot be distinguished from the j = 1 case. The results of state-of-the-art first-principles calculations for the reaction with the ground (j = 0) and excited (j = 1) rotational states are depicted by the green, blue and red curves in both panels. The interaction potential obtained with [CCSD(T)/aug-cc-pV6Z + mid-bond, green] alone erroneously predicts a low-energy resonance for para-hydrogen (j = 0) and two low-energy resonances for ortho-hydrogen (j = 1). Including the FCI/aug-cc-pVQZ correction (blue) allows for agreement down to collision energies corresponding to a few hundred millikelvin. Further improvement of the interaction potential is achieved by uniformly scaling the correlation energy by 0.4% (red), resulting in excellent agreement with the measured resonance positions and the overall behaviour of the rate coefficient down to the lowest collision energies probed in the experiment. The calculated rate coefficients are convoluted with the experimental resolution (8 mK) for the lowest collision energies. The error bars indicate the standard error in the rate coefficient and the collision energy, calculated according to 500 measurements per data point.
Conveniently, merged beam experiments with molecular hydrogen can be carried out with control over the rotational state of the molecule. A normal molecular hydrogen beam cooled in supersonic expansions consists of 75% ortho-hydrogen and 25% para-hydrogen. It follows from the Pauli principle that the lowest rotational state for para-hydrogen is j = 0 whereas j = 1 is the lowest molecular rotational state for ortho-hydrogen. A pure para-hydrogen sample can be prepared by catalytic conversion at cryogenic temperatures, allowing the determination of the state-selected rate coefficient, as has been described previously17.
In Fig. 1, we compare our experimental data to the results of first-principles calculations. A two-dimensional potential energy surface was obtained with the current gold standard of electronic structure theory, the coupled-cluster method with single, double and approximate non-iterative triple excitations [CCSD(T)], and further refined to include higher order correlation effects. Subsequently, the potential energy surface was used in quantum scattering calculations with reactive boundary conditions at short range24. The theoretical results demonstrate that collisions with j = 0 hydrogen are not sensitive to the anisotropic part of the interaction potential, such that the hydrogen molecule effectively behaves like an atom. Even scaling the anisotropic part, V2, by 50% does not introduce an observable change in the rate coefficient, as can be seen in the inset in Fig. 2. In stark contrast the j = 1 hydrogen rate coefficient is very sensitive to the anisotropy, emerging as shifts in the position of the orbiting resonance for different scaling factors of the anisotropic potential shown in Fig. 2.
The rate resulting from the original potential is depicted by the solid red curve, and the scaling of the anisotropic part by a factor of 1.5, 0.5 and 0.2 is depicted by the blue, magenta and green dashed curves, respectively. As the scaling factor decreases the lower-energy resonance position shifts to lower collision energies. The spectroscopic resolution of the resonance positions can serve as a sensitive measure of the anisotropy in the system. The logarithmic inset shows the rate for scaling factors of the anisotropic potential by the same factors for the reaction of He∗ + H 2 in the ground rotational state (j = 0). The rate coefficient remains the same for different scaling factors as the anisotropic potential has a limited contribution to this reaction.
The sensitivity of quantum resonance states to small changes in the interaction allows us to make a meaningful comparison of different levels of treating electron correlations in ab initio theory (Fig. 1). In fact, the interaction potential obtained with the ‘bare’ CCSD(T)/aug-cc-pV6Z + mid-bond method is not accurate enough to reproduce the low-energy resonances for collisions with both j = 0 and j = 1 H2 (see the green curves in Fig. 1). To account for higher-order electron correlation effects, the full configuration interaction (FCI/aug-cc-pVQZ) contribution beyond CCSD(T) has been calculated and added to the potential. The FCI-corrected potential energy surface performs significantly better (blue curves in Fig. 1), in particularly for collisions with H2(j = 1). However, it still erroneously predicts a resonance in the millikelvin range for H2(j = 0). To further improve the theoretical model, we have uniformly scaled the correlation energy. This is motivated by the fact that incompleteness of the orbital basis set is the main source of error in the ab initio calculations. It particularly affects the correlation energy, whereas the Hartree–Fock energy is almost fully converged in the aug-cc-pV6Z basis set (see Methods for details). In fact, increasing the correlation energy in the interaction potential by merely 0.4% leads to an excellent agreement for the resonance position of H2(j = 1) and confirms absence of this resonance for H2(j = 0) (red curves in Fig. 1). The latter can be understood as follows: scaling the correlation energy by 0.4% corresponds to increasing the depth of the isotropic potential by around 0.1 cm−1. This shifts the erroneous resonance obtained with CCSD(T) and CCSD(T) + δFCI down such that it becomes a truly bound state and does not affect the reaction rate.
A similar comparison of the different levels of theory and experiment could in principle also be performed using rovibrational spectroscopy of bound states. However, while spectroscopic methods measure the spacings between rovibrational states with high precision, these spacings are not sensitive to a global energy shift of the potential. In collisional spectroscopy the spectrum emerges above the dissociation threshold enabling the measurement of the energies of quasi-bound states on an absolute scale. Thus changes in the effective well depth due to the anisotropy are more pronounced in absolute scale measurements of the spectrum (Fig. 3).
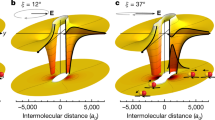
The potential curves are presented as a function of the He∗ –H2 distance in units of bohr radii (a0). All of the curves are asymptotically correlated to partial wave l = 3 and calculated according to adiabatic theory25. The adiabatic potentials shown in red and black correspond to the total angular momentum J = 3. The potential of j = 0 supports one bound state, located below the dissociation threshold at kB × 0.01 K. The contribution of the anisotropic part of the potential in the case of j = 1 (red curve) causes a reduction of the well depth. This reduction is sufficient to shift the bound state by ∼0.3 K placing it above the dissociation threshold (see the zoomed-in region in the inset), as depicted by the horizontal solid red line, leading to the resonance at 270 mK in the reaction rate coefficient of He∗ + H2 in the excited rotational state (j = 1). The grey curve corresponds to two nearly degenerate effective potential curves with a total angular momentum of J = 2 and J = 4 and with j = 1 H2. They support bound states at kB × 0.18 K below the dissociation threshold and no quasi-bound states. The bound and quasi-bound state wavefunctions for total angular momentum J = 3 are depicted by the black and red dashed curves, respectively. The resonance state wavefunction spans both the short- and the long-range part of the potential and can therefore be probed in collision experiments.
To qualitatively understand the role of anisotropy, it is convenient to consider the effective adiabatic interaction potentials. To this end, the interaction potential is expanded into two terms: V0(R), the isotropic term where R is the interparticle separation and V2(R)P2(cosθ), which describes the angular dependence to first order, where θ is the polar angle between the axis of the H2 molecule and the axis joining the H2 centre of mass with the He atom. We use an adiabatic theory25 inspired by previous works26,27 to construct effective potential curves that conserve the total angular momentum J. These potentials asymptotically correlate with a well-defined rotational state of H2(j) and a well-defined collisional angular momentum, that is, partial wave l. The anisotropy, V2(R), is small in our case compared with the rotational constant for all collision distances, such that mixing of the rotational states of the same parity in the H2 molecule is negligible. Figure 3 compares the three adiabatic potentials that support the lower-energy resonance state that asymptotically correlates with j = 0 and j = 1 H2 and orbital angular momentum (partial wave) l = 3. The black curve corresponding to J = 3 and j = 0 H2 is identical to the isotropic part of the interaction potential and includes the centrifugal term. It is deep enough to support a single bound state just below the threshold with a binding energy of kB × 0.01 K, as shown in the inset of Fig. 3. In the case of j = 1 H2, the anisotropy is responsible for reducing the well depth of the corresponding J = 3 effective potential, shown in red, enough to raise the bound state above the dissociation threshold (Fig. 3 inset). This state is located below the top of the centrifugal barrier, and is accessible via tunnelling in scattering experiments at a collision energy of kB × 270 mK. The grey adiabat in Fig. 3 represents two nearly degenerate effective potential curves with the total angular momentum of J = 2 and J = 4 and j = 1 H2. Both potentials do not support resonances and have bound levels at kB × 0.18 K below the dissociation threshold. Following a similar procedure, one can show that the higher-energy resonance, appearing for j = 0 as well as j = 1, asymptotically correlates with partial wave l = 4.
Orbiting resonances amplify minute differences in particle interactions, making them easily detectable in cold collision experiments provided that the energy resolution is sufficiently high. They are a manifestation of the quantization of the intermolecular degrees of freedom, which form a wave matter analogue of an optical cavity. Quantum resonances thus provide an ideal probe to illuminate the different contributions to particle interactions with a sensitivity that is a challenge for current state-of-the-art ab initio theory. The sensitivity of quantum resonances to the internal state of a molecule can be exploited in many experiments. Changing the rotational state of a molecule effectively switches the anisotropy of the interparticle interaction on and off, shifts resonance positions and thus dramatically changes the collisional cross-section. Such control over collisional properties can be critical to the success of molecular cooling methods that rely on collisions, such as evaporative or sympathetic cooling.
Methods
The experimental set-up, which has been discussed previously3,6,17, consists of two supersonic beams that are generated by pulsed Even–Lavie valves28 placed at a relative angle of 10°. The straight beam consists of noble gas mixtures of H2. The second beam consists of 4He, excited to He∗ using a dielectric barrier discharge29 that is located at the exit of the valve and is merged with the straight beam using a 20 cm magnetic guide, leading to zero relative angle between the beams at the detection region. The He∗ beam velocity is kept constant at 870 m s−1 while the H2 beam velocity is tuned by changing the valve temperature and seeding the H2 in noble carrier gas mixtures. The collision energy is determined by the relative mean velocity between the beams and the velocity distribution of each beam ranging from 300 K to 10 mK (ref. 23).
The metastable He beam is characterized using an on-axis multichannel plate. The H2 beam is characterized using a time-of-flight mass spectrometer (TOF-MS)30, which contains an additional ionization element. The TOF-MS is positioned perpendicular to the beams’ propagation, operating in a multi-pulsed mode, at 4 μs intervals. The reaction product ions are detected with the TOF-MS with the ionization element turned off, while the neutral molecules are characterized with the ionization element turned on. The relative rate coefficient is calculated according to the ratio between the measured signals of the products and reactants at each time interval. The rate coefficient is normalized to an absolute scale according to room-temperature thermal rate measurement of He(23S1) + H2 (ref. 31).
The para-H2 sample is prepared by liquefying normal H2 in liquid helium while in contact with the paramagnetic catalyst nickel sulfate. The sample is examined by resonance-enhanced multiphoton ionization followed by detection with the TOF-MS to determine its purity, showing that more than 98% of the H2 is in the ground rotational state, as previously described in detail32.
Rate coefficients were obtained by carrying out coupled-channel quantum reactive scattering calculations using a method24 in which only the reactant configuration is explicitly considered, and knowledge of the real value of the interaction energy is sufficient. This approach is based on the assumption that the reaction proceeds irreversibly once the reactants reach a sufficiently short interparticle distance Rc, the ‘capture radius’; and reactive collisions are simulated by imposing appropriate short-range boundary conditions. Such a quantum capture approach is particularly suitable for describing a chemi-ionization process because of its irreversibility and strongly exoenergetic character, which implies that the total rate coefficient is exclusively determined by the dynamics in the entrance channel of the reaction. As the real-valued Born–Oppenheimer interaction potential between He∗ and H2 does not include any coupling with the ionization continuum, He + H2+ + e−, we modified the purely repulsive wall of the potential, assuming that the isotropic part V0(R) is constant (Vc) at short intermolecular distance (R < Rc) and equal to the energy released in the ionization process, that is, V0(R) ≡ Vc = −3.646 eV if R ≤ Rc. This results in a barrier at short range and allows for the loss of the flux into the reactive channels via quantum tunnelling.
Close-coupling quantum scattering calculations were performed separately for collisions of He∗ with para-H2(j = 0) and with ortho-H2(j = 1). The angular basis functions were constructed as products of the rotational state of the H2 molecule and the partial wave describing the orbital motion of the whole complex, and were symmetry-adapted to values of the total angular momentum J and parity. The basis set was restricted to even or odd rotational states of H2 for collisions with para-H2, or ortho-H2, respectively. For collision energies up to 10 K, the basis set that yielded fully converged cross-sections included all of the relevant functions with j ≤ 4 and J < 8. The scattering wave functions were propagated from 7.0a0 to 200a0 by means of a renormalized Numerov propagator. The capture radius was determined by the condition that the elastic cross sections are fully converged; choosing a smaller Rc only results in a homogeneous scaling of the reaction rate coefficients, as does a modification of Vc. Short-range and asymptotic boundary conditions were imposed afterwards, as described in the original paper24. The calculated rate coefficients are convoluted with the experimental resolution, which is 8 mK for the lowest collision energies.
The potential energy surface was obtained using the counterpoise corrected supermolecular method in which the interaction energy is obtained as the difference of the total energy of the dimer (He∗ + H2) and the total energies of the monomers, calculated in the basis set of the dimer with basis functions placed at the position of the interacting partner with charges set to zero. As the He∗ + H2 system is not the actual triplet ground state of the system (which is He(11S) + 3Σ excited H2) we have employed the maximum overlap method33,34 with the orbitals corresponding to the isolated He∗ + H2 potential with an appropriate occupancy of 1s12s1σg2 as the starting point. The spin-restricted coupled-cluster method with single and double excitations with non-iterative corrections to triple excitations [CCSD(T)] in a very large basis set, now considered the gold standard of quantum chemistry, was employed, using the MOLPRO suite of codes35. The aug-mcc-pVXZ family for the hydrogen atom36 and the aug-cc-pVXZ family optimized for the triplet state of the metastable helium dimer37 were employed, where X = 4, 5, 6, 7 stands for the cardinal number, which corresponds to the highest angular momentum, equal to l = 3,4,5,6, respectively. To better account for the dispersion interaction we have also used a set of mid-bond functions located between the centre of mass of the H2 molecule and the He atom. These were obtained from polarization functions of hydrogen atom basis sets. The potential used in the subsequent scattering calculations was obtained with the aug-cc-pV6Z basis set. At large intermolecular separations, between R = 16a0 and R = 20a0, it was smoothly connected to the analytic long-range potential, employing a switching function38 and the long-range coefficients (C6 and C8) of ref. 39. The interatomic distance of the H2 molecule was set to 1.4487a0, which corresponds to the expectation value of the interatomic separation in the ground vibrational state of the hydrogen molecule. To ensure a proper convergence of the expansion into Legendre polynomials, the potential was calculated from 0° to 90° with a step of 15°. The projection onto Legendre polynomials was performed with a published integration procedure38.
The interaction energy was corrected beyond CCSD(T) with the correction obtained as the difference between the coupled-cluster method with fourth-fold excitations (CCSDTQ) and CCSD(T) in the same basis set. Owing to the enormous numerical cost, CCSDTQ calculations, which are equivalent to FCI for a four-electron system and exact for a given basis set, were performed only for linear- and T-shape geometries, with a smaller basis set, aug-cc-pVQZ and no mid-bond functions, using the CFOUR package (http://www.cfour.de) interfaced with the MRCC programme40. The dominant source of uncertainty of the potential energy surface is incompleteness of the basis set, whereas relativistic effects and the diagonal Born–Oppenheimer (DBO) correction were found to be negligible: relativistic effects, estimated by calculating the scalar relativistic perturbation correction (mass velocity and one-electron Darwin term) are of the order of 0.01 cm−1 in the global minimum with a well depth of 14.30 cm−1 at 10.5a0. The DBO correction was obtained as the difference between the corrections for the dimer and infinitely separated monomers for T-shape and L-shape geometries, calculated with the aug-cc-pVQZ basis set and the Hartree–Fock wavefunction (it is not sensitive to the size of the basis set nor the quality of the wavefunction). The contribution of the DBO correction to V0 is 0.044 cm−1 in the global minimum. The incompleteness of the basis set only affects the correlation energy, whereas the Hartree–Fock interaction energy is converged to within 0.01 cm−1 in our calculations. Truncation of the basis set results in a shallower potential and an inner turning point that is slightly shifted towards larger intermolecular distances. The limit of the basis set is estimated assuming a convergence pattern A + BX−3 or A + BX−3 + CX−5 for singlet systems and A + BX−5 for triplet helium as the correlation energy was found to converge with the cardinal number as X−3 for singlet electron pairs and as X−5 for triplet pairs41,42. The correlation energy in the H2 and He∗ monomers are very different in magnitude (9,031 ± 1 cm−1 compared with 214.7 ± 0.01 cm−1). For the total system, the basis set limit for the CCSD(T) calculations in the global minimum extrapolated from the aug-cc-pV6Z and aug-cc-pV7Z basis sets (in the latter case we could afford for such calculations for single geometry) is −14.62 cm−1, whereas extrapolation from the X = 5,6,7 basis set yields the limit −14.42 cm−1. As a conservative estimate, we take the difference between the potential obtained in aug-cc-pV6Z and the basis set limit extrapolated from X = 6,7 as the uncertainty of the potential.
Data availability.
The data that support the plots within this Letter and other findings of this study are available from the corresponding author upon reasonable request.
References
Ni, K.-K. et al. Dipolar collisions of polar molecules in the quantum regime. Nature 464, 1324–1328 (2010).
de Miranda, M. H. G. Controlling the quantum stereodynamics of ultracold bimolecular reactions. Nat. Phys. 7, 502–507 (2011).
Henson, A. B., Gersten, S., Shagam, Y., Narevicius, J. & Narevicius, E. Observation of resonances in Penning ionization reactions at sub-kelvin temperatures in merged beams. Science 338, 234–238 (2012).
Chefdeville, S. et al. Observation of partial wave resonances in low-energy O2-H2 inelastic collisions. Science 341, 1094–1096 (2013).
Costes, M. & Naulin, C. Observation of quantum dynamical resonances in near cold inelastic collisions of astrophysical molecules. Chem. Sci. 7, 2462–2469 (2016).
Lavert-Ofir, E. et al. Observation of the isotope effect in sub-kelvin reactions. Nat. Chem. 6, 332–335 (2014).
Vogels, S. N. et al. Imaging resonances in low-energy NO–He inelastic collisions. Science 350, 787–790 (2015).
Bergeat, A., Onvlee, J., Naulin, C., van der Avoird, A. & Costes, M. Quantum dynamical resonances in low-energy CO(j = 0) + He inelastic collisions. Nat. Chem. 7, 349–353 (2015).
Ashfold, M. N. R. et al. Imaging the dynamics of gas phase reactions. Phys. Chem. Chem. Phys. 8, 26–53 (2006).
Kitsopoulos, T. N., Buntine, M. A., Baldwin, D. P., Zare, R. N. & Chandler, D. W. Reaction product imaging: the H + D2 reaction. Science 260, 1605–1610 (1993).
Lin, J. J., Zhou, J., Shiu, W. & Liu, K. State-specific correlation of coincident product pairs in the F + CD4 reaction. Science 300, 966–969 (2003).
Kohguchi, H., Suzuki, T. & Alexander, M. H. Fully state-resolved differential cross sections for the inelastic scattering of the open-shell NO molecule by Ar. Science 294, 832–834 (2001).
van der Avoird, A. & Nesbitt, D. J. Rovibrational states of the H2O–H2 complex: an ab initio calculation. J. Chem. Phys. 134, 044314 (2011).
Lovejoy, C. M., Nelson, D. D. & Nesbitt, D. J. Hindered internal rotation in jet cooled H2 HF complexes. J. Chem. Phys. 87, 5621–5628 (1987).
Carr, L. D., DeMille, D., Krems, R. V. & Ye, J. Cold and ultracold molecules: science, technology and applications. New J. Phys. 11, 055049 (2009).
Hall, F. H. J. & Willitsch, S. Millikelvin reactive collisions between sympathetically cooled molecular ions and laser-cooled atoms in an ion-atom hybrid trap. Phys. Rev. Lett. 109, 233202 (2012).
Shagam, Y. et al. Molecular hydrogen interacts more strongly when rotationally excited at low temperatures leading to faster reactions. Nat. Chem. 7, 921–926 (2015).
Hauser, D. et al. Rotational state-changing cold collisions of hydroxyl ions with helium. Nat. Phys. 11, 467–470 (2015).
Maier, T. et al. Emergence of chaotic scattering in ultracold Er and Dy. Phys. Rev. X 5, 041029 (2015).
Simbotin, I. & Côté, R. Effect of nuclear spin symmetry in cold and ultracold reactions: D + para/ortho-H2 . New J. Phys. 17, 065003 (2015).
Lique, F., Li, G., Werner, H.-J. & Alexander, M. H. Communication: non-adiabatic coupling and resonances in the F + H2 reaction at low energies. J. Chem. Phys. 134, 231101 (2011).
Chefdeville, S. et al. Experimental and theoretical analysis of low-energy CO + H2 inelastic collisions. Astrophys. J. 799, L9 (2015).
Shagam, Y. & Narevicius, E. Sub-Kelvin collision temperatures in merged neutral beams by correlation in phase-space. J. Phys. Chem. C 117, 22454–22461 (2013).
Janssen, L. M. C., van der Avoird, A. & Groenenboom, G. C. Quantum reactive scattering of ultracold NH(X3Σ−) radicals in a magnetic trap. Phys. Rev. Lett. 110, 063201 (2013).
Pawlak, M., Shagam, Y., Narevicius, E. & Moiseyev, N. Adiabatic theory for anisotropic cold molecule collisions. J. Chem. Phys. 143, 074114 (2015).
Holmgren, S. L., Waldman, M. & Klemperer, W. Internal dynamics of van der Waals complexes. I. Born–Oppenheimer separation of radial and angular motion. J. Chem. Phys. 67, 4414–4422 (1977).
Scribano, Y., Faure, A. & Lauvergnat, D. Rotational excitation of H2O by para-H2 from an adiabatically reduced dimensional potential. J. Chem. Phys. 136, 094109 (2012).
Even, U., Jortner, J., Noy, D., Lavie, N. & Cossart-Magos, C. Cooling of large molecules below 1 K and He clusters formation. J. Chem. Phys. 112, 8068–8071 (2000).
Luria, K., Lavie, N. & Even, U. Dielectric barrier discharge source for supersonic beams. Rev. Sci. Instrum. 80, 104102 (2009).
Wiley, W. C. & McLaren, I. H. Time-of-flight mass spectrometer with improved resolution. Rev. Sci. Instrum. 26, 1150–1157 (1955).
Veatch, G. E. & Oskam, H. J. Collision processes occurring in decaying plasmas produced in helium-hydrogen mixtures. Phys. Rev. A 8, 389–396 (1973).
Pratt, S. T., Dehmer, P. M. & Dehmer, J. L. Photoionization of excited molecular states. H2 C1Πu . Chem. Phys. Lett. 105, 28–33 (1984).
Gilbert, A. T. B., Besley, N. A. & Gill, P. M. W. Self-consistent field calculations of excited states using the maximum overlap method (MOM). J. Phys. Chem. A 112, 13164–13171 (2008).
Hapka, M., Chałasiński, G., Kłos, J. & Żuchowski, P. S. First-principle interaction potentials for metastable He(3S) and Ne(3P) with closed-shell molecules: application to Penning-ionizing systems. J. Chem. Phys. 139, 014307 (2013).
Werner, H.-J., Knowles, P. J., Knizia, G., Manby, F. R. & Schütz, M. Molpro: a general-purpose quantum chemistry program package. WIREs Comput. Mol. Sci. 2, 242–253 (2012).
Mielke, S. L., Garrett, B. C. & Peterson, K. A. A hierarchical family of global analytic Born–Oppenheimer potential energy surfaces for the H + H2 reaction ranging in quality from double-zeta to the complete basis set limit. J. Chem. Phys. 116, 4142 (2002).
Przybytek, M. & Jeziorski, B. Bounds for the scattering length of spin-polarized helium from high-accuracy electronic structure calculations. J. Chem. Phys. 123, 134315 (2005).
Janssen, L. M. C., Groenenboom, G. C., van der Avoird, A., Żuchowski, P. S. & Podeszwa, R. Ab initio potential energy surfaces for NH(3Σ−)-NH(3Σ−) with analytical long range. J. Chem. Phys. 131, 224314 (2009).
Bishop, D. M. & Pipin, J. Dipole, quadrupole, octupole, and dipole–dipole–quandrupole polarizabilities and second hyperpolarizabilities at real and imaginary frequencies for helium in the 23S state: Dispersion-energy coefficients for interactions between He(23S) and H(12S), He(11S) He(23S), or H2(X1Σg+). Int. J. Quantum Chem. 47, 129–134 (1993).
Rolik, Z., Szegedy, L., Ladjánszki, I., Ladóczki, B. & Kállay, M. An efficient linear-scaling CCSD(T) method based on local natural orbitals. J. Chem. Phys. 139, 094105 (2013).
Helgaker, T., Klopper, W., Koch, H. & Noga, J. Basis-set convergence of correlated calculations on water. J. Chem. Phys. 106, 9639–9646 (1997).
Kutzelnigg, W. & Morgan, J. D. Rates of convergence of the partial-wave expansions of atomic correlation energies. J. Chem. Phys. 96, 4484–4508 (1992).
Acknowledgements
The authors acknowledge financial support from the European Commission through ERC Grant EU-FP7-ERC-CoG 1485 QuCC. Additional financial support from the German–Israeli Foundation (Grant no. 1254), the COST Action MOLIM (CM1405) and the Polish National Science Center (Grant no. DEC-2012/07/B/ST2/00235) is acknowledged. This research was also supported by the I-Core (the Israeli Excellence Center) ‘Circle of Light’, by the Israel Science Foundation Grant nos 298/11 and 1530/15.
Author information
Authors and Affiliations
Contributions
All authors contributed to all aspects of this work.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
About this article
Cite this article
Klein, A., Shagam, Y., Skomorowski, W. et al. Directly probing anisotropy in atom–molecule collisions through quantum scattering resonances. Nature Phys 13, 35–38 (2017). https://doi.org/10.1038/nphys3904
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys3904
This article is cited by
-
Attosecond photoionisation time delays reveal the anisotropy of the molecular potential in the recoil frame
Nature Communications (2022)
-
Anisotropic dynamics of resonant scattering between a pair of cold aligned diatoms
Nature Chemistry (2022)
-
Mapping partial wave dynamics in scattering resonances by rotational de-excitation collisions
Nature Chemistry (2022)
-
Evidence for the association of triatomic molecules in ultracold 23Na40K + 40K mixtures
Nature (2022)
-
A driven three-dimensional electric lattice for polar molecules
Frontiers of Physics (2022)