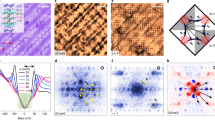
Abstract
It is widely believed that high-temperature superconductivity in the cuprates emerges from doped Mott insulators1. When extra carriers are inserted into the parent state, the electrons become mobile but the strong correlations from the Mott state are thought to survive—inhomogeneous electronic order, a mysterious pseudogap and, eventually, superconductivity appear. How the insertion of dopant atoms drives this evolution is not known, nor is whether these phenomena are mere distractions specific to hole-doped cuprates or represent genuine physics of doped Mott insulators. Here we visualize the evolution of the electronic states of (Sr1−xLax)2IrO4, which is an effective spin-1/2 Mott insulator like the cuprates, but is chemically radically different2,3. Using spectroscopic-imaging scanning tunnelling microscopy (SI-STM), we find that for a doping concentration of x ≈ 5%, an inhomogeneous, phase-separated state emerges, with the nucleation of pseudogap puddles around clusters of dopant atoms. Within these puddles, we observe the same iconic electronic order that is seen in underdoped cuprates1,4,5,6,7,8,9. We investigate the genesis of this state and find evidence at low doping for deeply trapped carriers, leading to fully gapped spectra, which abruptly collapse at a threshold of x ≈ 4%. Our results clarify the melting of the Mott state, and establish phase separation and electronic order as generic features of doped Mott insulators.
Similar content being viewed by others
Main
A core mystery of condensed matter physics is how the rigid arrangement of electrons in Mott insulators loosens when inserting electrons or holes, and how this leads to exotic states inside the Mott gap (Fig. 1). In the cuprate high-temperature superconductors, this process might be the cause of their poorly understood, remarkably complex behaviour. Most prominent is the formation of a pseudogap and a variety of inhomogeneous electronic orders1,4,5,6,7,8,9, sometimes described as intertwined10. This phenomenology has often been assumed (but not verified) to be generic of melting spin-1/2 Mott physics and not just specific to cuprates. In this Letter we show that an inhomogeneous electronic phase separation as well as a local glassy, stripy charge order exist in a chemically completely different two-dimensional Mott insulator, revealing an universality of these emergent phenomena.
a, In Mott insulators, the electronic states split into a lower and upper Hubbard band (LHB and UHB) separated by the Mott gap. b, The gap is caused by the on-site interaction U that prevents electrons from hopping from site to site with energy gain t . c,d, When doping with charge carriers, new states move into the Mott gap in unknown ways. e, Atomically resolved topograph with a doping concentration 2.2% (see Supplementary Sections 2 and 3). The La3+ dopant atoms are readily identified as dark spots surrounded by brighter atoms (red square)13. f, Atomically resolved topograph with a doping concentration of 5.0%. See Supplementary Section 2 for more topographic images, and Supplementary Section 3 for information on how we count the dopant atoms with precision of ±0.7%.
To this end, we create (Sr1−xLax)2IrO4 samples with a range of different lanthanum doping concentrations x, 0 < x < 6% (see Methods and Supplementary Section 1). This material can be seen as a quasi-two-dimensional, electron-doped Mott insulator similar to the cuprates despite a very different chemical make-up. The x = 0 parent material consists of alternating IrO2 and SrO planes, such that oxygen octahedra form around each iridium atom. The five valence electrons in the outer Ir 5d shell are split by crystal field and strong spin–orbit coupling to form a filled Jeff,3/2 and a half filled Jeff,1/2 band. The moderate on-site repulsion U is then sufficient to open a Mott gap in the Jeff,1/2 band, making Sr2IrO4 an effective spin-1/2 Mott insulator (Fig. 1a, b)3. In contrast to hole doping in the cuprates, which is often interstitial oxygen doping, La3+ substitutions on the Sr site provide electron doping for the iridates (Fig. 1c, d). The resulting electronic structure is sometimes predicted to become high-temperature superconducting upon sufficient doping11,12.
Figure 1e, f depicts typical topographs on atomically flat, SrO terminated surfaces for different doping concentrations; the SrO lattice is visible with lattice constant a0 = 3.9 Å and the white squares identify the positions of La dopant atoms in the same layer13. The ability to identify the dopant positions easily with atomic precision on the topographs (for example, in contrast to the cuprates14,15) is key to this investigation, as it allows one to precisely localize dopant atoms, even when samples show micrometre variations of the dopant concentration (Supplementary Sections 2 and 3). For this study, we investigate surfaces with local doping concentrations of 2.1%, 2.2%, 2.3%, 3.7%, 4.8%, 5.0%, 5.2%, 5.5% to obtain a full overview of the doping evolution.
We start our discussion with the very lightly doped samples, which are deep in the Mott phase. A typical topograph of a sample with 2.2% dopant concentration is shown in Fig. 1e. In all our measurements, this doping level yields a clear Mott gap, as shown in Fig. 2a. The shape of the gap is reminiscent of STM spectra of cuprate parent materials5,6,7,16. We describe in Supplementary Section 4, how the poor screening in lightly doped Mott insulators leads to an additional potential that decays inside the sample, commonly called tip-induced band bending17,18, yielding an apparent energy gap larger than the true Mott gap, ΔMottapp ≫ ΔMott, which makes the gap roughly consistent with optical measurements19.
a, Mott gap map ΔMott of a sample with a doping concentration of x = 2.2% . Positions of dopant atoms are indicated by green circles. The inset shows local density of states spectra averaged inside the white circles. An additional density of states at around −0.8 V is visible in the low-gap regions, and might be related to the impending collapse of the impurity Mott state discussed later. b, Local density of states spectra along the green line in a, each with an offset on the vertical axis.
To investigate how the Mott state reacts when dopant atoms are inserted, we acquire atomic-scale Mott maps—that is, the magnitude of the Mott gap as a function of location, ΔMott(r)—while measuring the dopant positions on the atomic scale. Each Mott map is extracted from a set of differential conductance spectra measured on a grid (rx, ry). Figure 2a shows the result on a 2.2% sample; the dopant atoms are marked by green dots. La dopants do not significantly change the Mott gap size in their close vicinity; instead, they induce or pin long-wavelength arrangement of varying Mott gap. We interpret these nanoscale arrangements as the first of a series of orders that appear upon doping. The most surprising observation, however, is the total lack of in-gap states, despite the presence of dopants—a mystery to which we shall return towards the end of this Letter.
The pure Mott state described thus far is not sustained at doping levels above ∼5%. At that point, we discover an abrupt transition to a strikingly inhomogeneous electronic structure: a phase-separated Mott/pseudogap landscape20,21,22. Some regions still exhibit a pure Mott gap; in contrast to the very low doping samples, now the Fermi level is pinned closer to the bottom of the upper Hubbard band, (blue curve in Fig. 3a), as expected for a Mott insulator doped with free carriers (similar to electron doped-bi-layer iridate23 and opposite to hole-doped cuprates6). Additionally, there are regions where we measure electronic states inside the Mott gap (red curve in Fig. 3a). Here, the spectra are remarkably similar to the pseudogap in the cuprates4,5,6, with a gap value of around 70–300 meV, in rough agreement with recent photoemission measurements that extracted the leading edge gap24,25,26, and with some spectra showing clear ‘coherence peaks’ (Fig. 3d). We will refer to these regions as ‘pseudogap puddles’. They are not randomly distributed, but form around regions with clusters of dopant atoms. Importantly, we do not observe pseudogap puddles in lightly doped samples, even if a few dopants happen to be close together by chance; a certain threshold in the doping level is needed for the transition to occur.
a, Different spectra in the phase-separated region: Mott like spectrum (blue), with the chemical potential pinned to the UHB, and mixed Mott/pseudogap spectrum (red). The spectra are the average of 180 spectra inside the white circles in c. b, Phenomenological fit function to simultaneously extract both the Mott and pseudogap size. It consists of a density of states (dot-dashed) multiplied by the Mott gap (dashed) plus states inside the Mott gap with a V-shaped pseudogap (dotted). See Supplementary Section 6 for details. c, The Mott parameter as defined in the text identifies pseudogap puddles (red) and pure Mott regions (blue). Green circles indicate La dopant locations. The triangle on the colour bar indicates the value of the black contour. Inset, definition of the Mott parameter: the integrated DOS inside Mott gap (red) normalized by the one outside the gap (blue). d, Local density of states spectra along the white line in c (each corresponding to a single measurement). The separation is sharp in the sense that a Mott spectrum becomes a pseudogap spectrum within roughly a nanometre. e, ΔPG map extracted from the fitting procedure (for ΔMott, see Supplementary Section 7). The square indicates the region displayed in Fig. 4. Inset, the correlation between ΔMott and ΔPG.
To further analyse this phase-separated landscape, it is necessary to establish the spatial distribution of the Mott/pseudogap character. To do so, we introduce a ‘Mott parameter’ M(r) by integrating the density of states inside the putative Mott gap and normalize it by the integrated density of states outside the gap, M(r) = ∫ −350 meV+50 meVLDOS(E)dE/∫ +200 meV+500 meVLDOS(E)dE (Fig. 3c, inset). This parameter is large when there are states inside the gap, and small when the Mott gap is dominating. Plotting M(r) as a function of the spatial coordinates reveals the nanoscale character of the phase separation, with pseudogap puddles within regions of pure Mott gap. The phase separation is well defined and sharp, in the sense that the transition from pure Mott area to a pseudogap puddle occurs within less than a nanometre (Fig. 3d). This allows us to define a threshold for Mott and pseudogap regions (black contour in Fig. 3c).
We then develop a fitting procedure that is able to fit spectra both in the Mott regions and in the pseudogap puddles. The fitting function includes a phenomenological Mott gap, and additional density of states within that is gapped by a phenomenological pseudogap based on photoemission results25,26 and commonly used in the cuprates7,27 (Fig. 3b and Methods). This function allows one to simultaneously extract both the pseudogap ΔPG (Fig. 3e) and the Mott gap ΔMott (Supplementary Section 7) for ∼105 spectra located in the pseudogap puddles and to calculate the correlations between the two gaps. If the magnetic correlations J in the t-J model are directly causing order that manifests the pseudogap, one could expect an anti-correlation between ΔPG and ΔMott, as J ∼ t2/U. Intriguingly, within the puddles, our data show a clear positive correlation of 0.31—that is, the larger the Mott gap, the larger the pseudogap (Fig. 3e, inset). This is evidence that pseudogap and Mott physics are intimately linked1,28, but suggests that it is not simply the magnetic correlations that cause the pseudogap.
To further test if the cuprate phenomenology is universal to lightly doped Mott insulators, we search for ordered phases on our samples. In the cuprates, it has become very clear that a sizable set of (possibly intertwined) orders coexist, perhaps causing the pseudogap1. These include disordered stripy charge arrangements, sometimes referred to as glassy order or charge density waves1,4,5,6,7,8,9,10. Indeed, we find that the spatial distribution of the pseudogap value, when extracted with atomic precision, reveals a striking tendency for order. The ΔPG gap maps exhibit glassy, locally unidirectional structures (Figs 3e and 4a), reminiscent of lightly hole-doped cuprates4,5,6,7,8 (see Supplementary Section 5). Glassy charge order is also visible in the density of states right outside the pseudogap, for example, at −210 meV shown in Fig. 4b, c. The arrangements consist of bond centred, unidirectional objects of length scales of 2 to 4 Ir–Ir distances, clearly very disordered on a larger length scale. These arrangements, like the pseudogap puddles, nucleate around the dopant atom positions (green circles).
a, Map of the pseudogap ΔPG. The small green dots indicate Ir atom locations, the larger green circles indicate La dopant locations on the Sr site. Disordered, locally unidirectional patterns are visible. The inset shows a series of spectra along the white line. The colour indicates the gap value. b, Density of states at −210 meV. Glassy order is nucleating around the La dopant atoms. c, Laplacian of the ratio map at −210 meV.
Next, we want to elucidate how this inhomogeneous, charge-ordered pseudogap state emerges from the fully gapped state at low doping, by using the unique availability of samples with densely spaced doping concentrations in the iridate family. We measure one or more spectroscopic-imaging maps with >106 data-points at each doping concentration, and we analyse each using the methods described above. Figure 5 summarizes the results, illustrating the abrupt nature of the transition. Figure 5a shows the evolution of the averaged spectra in the regions with pseudogap (red) and in those without (blue), Fig. 5b–g shows the phase separation on the respective field of views as defined by the Mott parameter defined above.
a, Density of states spectra at different doping levels, each corresponding to the Mott parameter panels b–g directly on the right. Each set of spectra is averaged over regions with Mott gap (blue) and pseudogap (red) as defined by the Mott parameter in b–g. The spectra from top to bottom with decreasing doping correspond to the respective panels b–g. At around 5%, the phase separation abruptly starts. b–g, Respective maps of the Mott parameter, where blue indicates a pure Mott gap, and red indicates a pseudogap puddle. Increasing doping leads to smaller pure Mott areas. h, Schematic image of an impurity Mott transition, with the split impurity band states, (not) including the energy splitting Δcharging in (light) green.
At doping concentration below the transition threshold, none of the spectra exhibit any sort of impurity state. Nor is the chemical potential pinned to one of the edges of the Mott gap, as one would expect from a Mott insulator with free carriers from shallow dopant centres. Combined with the fact that the phenomenology of the electronic structure is surprisingly independent of the doping concentration below ∼4%, this leads to the question: Where did all the dopant electrons go? We propose the scenario illustrated in Fig. 5h. Tightly bound dopant electrons at the dopant locations lead to a putative dopant band (impurity band in semiconductor parlance) inside the gap which keeps the chemical potential around mid-gap. Because the extra electrons from the La3+ dopants reside in the upper Hubbard band in the IrO layer, they experience the strong Mott correlations. Consequently, the charging energy E = e2/C to remove or add electrons (or holes) to the [La3+ + e−] bound state is large enough to split the dopant band and push it outside the Mott gap (Fig. 5h). An equivalent way of describing this, going back to N.F. Mott, is that there is a Mott transition in the dopant band29. With increasing doping, screening of the long-range Coulomb interaction by doped carriers leads to an abrupt collapse of the impurity Mott state at doping concentrations lower than one would expect in a static picture. In the cuprates, similar microscopic processes have initially been proposed, but the Mott state is much more fragile: even weak doping of around 2% can destroy the logarithmic divergence in the resistance30. This is due to the much smaller energy scales of the trapping in the cuprates; below the transitions, the material behaves similarly to a doped semiconductor, with an impurity band close to the energy of the valence band30. This is consistent with the later observation that the dopant centres are fairly shallow6. On the basis of our results, we predict that LDA + U calculations3,31 on doped iridates will reveal the trapping of La dopant states to be much deeper than the equivalent states in the cuprates, and that samples with greater homogeneity will reveal a very sharp impurity band metal–insulator transition.
Finally, we would like to go back to the comparison between the electron-doped iridate material studied here and the cuprates. Detailed measurements on the cuprates, for example, Ca2−xNaxCuO2Cl2 and Bi2Sr2CaCu2O8+δ, revealed surprising universalities, including the glassy charge order observed in the CuO layer. At first glance, (Sr1−xLax)2IrO4 seems to be a very different beast: electron instead of hole doping, Ir instead of Cu, 5d5 instead of 3d9. However, our data clearly show that the physics of electronic order and the pseudogap are not specific to the cuprates but generic to lightly doped Mott insulators, and we believe that the interplay between dopants and order seen here holds for the cuprates as well. By extension, we can expect (Sr1−xLax)2IrO4 to become a high-temperature superconductor with only a slightly higher doping concentration.
Methods
Experimental set-up.
The STM experiments are performed with a modified, low-temperature, ultrahigh vacuum STM system from Unisoku. The (Sr1−xLax)2IrO4 crystals are cleaved in situ at temperature T ∼ 20 K and base pressure p = 2 × 10−10 mbar, and then transferred immediately into the STM sample stage. All STM results reported in this paper are acquired in cryogenic vacuum at temperatures of either T ≈ 2 K or T ≈ 7 K (no significant difference in our measurements has been observed between these temperatures). The STM topographs are taken in the constant current mode, and the dI/dV spectra are collected using a standard lock-in technique with modulation frequency f = 857 Hz. Importantly, we set each spectrum up at Ibias and Vbias, and then sweep all the voltages. We use mechanically ground PtIr tips for all the measurements. We always test the spectroscopic and topographic properties of the tips on a crystalline Au(111) surface prepared in situ by Ar ion sputtering and temperature annealing before measuring (Sr1−xLax)2IrO4.
The topographs in Fig. 1e, f are set up at −1.2 V, 200 pA. The map in Fig. 2 is set up at 1.2 V, 500 pA. The map in Figs 3 and 4 is set up at 460 mV, 300 pA. The maps in Fig. 5 are set up as follows: Fig. 5b: 460 mV, 300 pA; Fig. 5c: −0.4 V, 250 pA; Fig. 5d: −1.2 V, 700 pA; Fig. 5e: 0.9 V, 220 pA, Fig. 5f: 1.2 V, 250 pA; Fig. 5g: 1.2 V, 250 pA.
(Sr1−xLax)2IrO4 samples.
As described in ref. 25, the (Sr1−xLax)2IrO4 single crystals are flux grown from a mixture of off-stoichiometric quantities of IrO2, La2O3 and SrCO3 in an anhydrous SrCl2 flux. The mixture is heated to 1,245 °C for 12 h and cooled at a rate of 8 °C h−1 to 1,100 °C before quenching to room temperature. The resulting crystals are mechanically separated from the flux by washing with water. Resistivity curves at different doping concentrations x (as determined by energy dispersive X-ray spectroscopy (EDX)) are shown in Supplementary Section 1.
Extraction of ΔMott and ΔPG.
To fit the vastly different spectra both in the Mott region and in the pseudogap puddles, we develop a fitting procedure as follows. We start with a smooth polynomial background density of states DOSBG(E) = aE2 + c, where E is the energy, and a and c are fitting parameters. Next, we multiply it by a phenomenological Mott gap ΔMott consisting of two slightly broadened gap edges, asymmetric around the chemical potential:

The gap edges are broadened by w, E0 is the energy where the upper Hubbard band roughly pins to the chemical potential and ΔMott is the size of the Mott gap. We keep the first two parameters fixed (w = 0.026 eV, E0 = 0.1 eV), while the size of the Mott gap ΔMott is used as a fitting parameter. We then allow for states inside the Mott gap that are gapped by introducing a phenomenological function based on photoemission results25,26 and commonly used in the cuprates7,27. This part allows the extraction of the pseudogap value ΔPG.

This function contains two fitting parameters: a scaling factor C0 and the size of the pseudogap ΔPG. We keep α, an effective scattering rate, fixed to 0.2 eV0.5. The square root in the imaginary part of the self-energy is selected to ensure a rather constant broadening independent of the gap. Albeit DOSPG(E) is inspired by recent photoemission results and experiences from the cuprates26,27, we emphasize that our motivation was to extract the key physical quantities with few fitting parameters. We expect future theoretical progress to yield even better, less phenomenological, fit functions.
At each point of the spectroscopy map the data is fitted with the constructed fit function, using the least squares method. The initial guess is provided by fitting the average of all spectra in the data set. Since in the high-doping regime the upper edge of the Mott gap is pinned to the chemical potential, and because in that location pseudogap and Mott gap overlap, we fit the model to the data only for negative energies. The resulting model is an excellent fit to all the spectra measured on the x > 4% samples, as shown in the Supplementary Section 6.
Data availability.
The data that support the plots within this paper and other findings of this study are available from the corresponding author upon reasonable request.
References
Keimer, B., Kivelson, S. A., Norman, M. R., Uchida, S. & Zaanen, J. From quantum matter to high-temperature superconductivity in copper oxides. Nature 518, 179–186 (2015).
Rau, J. G., Lee, E. K.-H. & Kee, H.-Y. Spin-orbit physics giving rise to novel phases in correlated systems: iridates and related materials. Annu. Rev. Condens. Matter Phys. 7, 195–221 (2016).
Kim, B. J. et al. Novel Jeff = 1/2 Mott state induced by relativistic spin-orbit coupling in Sr2IrO4 . Phys. Rev. Lett. 101, 076402 (2008).
Fujita, K. et al. Spectroscopic Imaging STM: Atomic-Scale Visualization of Electronic Structure and Symmetry in Underdoped Cuprates Ch. 3 (Springer, 2012).
Kohsaka, Y. et al. Imaging nanoscale electronic inhomogeneity in the lightly doped Mott insulator Ca2−xNaxCuO2Cl2 . Phys. Rev. Lett. 93, 097004 (2004).
Cai, P. et al. Visualizing the evolution from the Mott insulator to a charge-ordered insulator in lightly doped cuprates. Nat. Phys. http://dx.doi.org/10.1038/nphys3840 (2016).
Kohsaka, Y. et al. Visualization of the emergence of the pseudogap state and the evolution to superconductivity in a lightly hole-doped Mott insulator. Nat. Phys. 8, 534–538 (2012).
Parker, C. V. et al. Fluctuating stripes at the onset of the pseudogap in the high-Tc superconductor Bi2Sr2CaCu2O8+x . Nature 468, 677–680 (2010).
Comin, R. & Damascelli, A. Resonant X-ray scattering studies of charge order in cuprates. Annu. Rev. Condens. Matter Phys. 7, 369–405 (2016).
Fradkin, E., Kivelson, S. A. & Tranquada, J. M. Colloquium: theory of intertwined orders in high temperature superconductors. Rev. Mod. Phys. 87, 457–482 (2015).
Wang, F. A. & Senthil, T. Twisted Hubbard model for Sr2IrO4: magnetism and possible high temperature superconductivity. Phys. Rev. Lett. 106, 136402 (2011).
Watanabe, H., Shirakawa, T. & Yunoki, S. Monte Carlo study of an unconventional superconducting phase in iridium oxide Jeff = 1/2 Mott insulators induced by carrier doping. Phys. Rev. Lett. 110, 027002 (2013).
Okada, Y. et al. Imaging the evolution of metallic states in a correlated iridate. Nat. Mater. 12, 707–713 (2013).
McElroy, K. et al. Atomic-scale sources and mechanism of nanoscale electronic disorder in Bi2Sr2CaCu2O8+δ . Science 309, 1048–1052 (2005).
Zeljkovic, I. et al. Imaging the impact of single oxygen atoms on superconducting Bi2+ySr2−yCaCu2O8+x . Science 337, 320–323 (2012).
Ye, C. et al. Visualizing the atomic-scale electronic structure of the Ca2CuO2Cl2 Mott insulator. Nat. Commun. 4, 1365 (2013).
Feenstra, R. M., Dong, Y., Semtsiv, M. P. & Masselink, W. T. Influence of tip-induced band bending on tunnelling spectra of semiconductor surfaces. Nanotechnology 18, 044015 (2007).
Wijnheijmer, A. P. et al. Single Si dopants in GaAs studied by scanning tunneling microscopy and spectroscopy. Phys. Rev. B 84, 125310 (2011).
Moon, S. J. et al. Temperature dependence of the electronic structure of the Jeff 1/2 Mott insulator. Phys. Rev. B 80, 195110 (2009).
Chen, X. et al. Influence of electron doping on the ground state of (Sr1−xLax)2IrO4 . Phys. Rev. B 92, 075125 (2015).
Yan, Y. J. et al. Electron-doped Sr2IrO4: an analogue of hole-doped cuprate superconductors demonstrated by scanning tunneling microscopy. Phys. Rev. X 5, 041018 (2015).
Dai, J., Calleja, E., Cao, G. & McElroy, K. Local density of states study of a spin-orbit-coupling induced Mott insulator Sr2IrO4 . Phys. Rev. B 90, 041102 (2014).
He, J. et al. Spectroscopic evidence for negative electronic compressibility in a quasi-three-dimensional spin-orbit correlated metal. Nat. Mater. 14, 577–582 (2015).
Kim, Y. K. et al. Fermi arcs in a doped pseudospin-1/2 Heisenberg antiferromagnet. Science 345, 187–190 (2014).
de la Torre, A. et al. Collapse of the Mott gap and emergence of a nodal liquid in lightly doped Sr2IrO4 . Phys. Rev. Lett. 115, 176402 (2015).
Kim, Y. K., Sung, N. H., Denlinger, J. D. & Kim, B. J. Observation of a d-wave gap in electron-doped Sr2IrO4 . Nat. Phys. 12, 37–41 (2015).
Alldredge, J. W. et al. Evolution of the electronic excitation spectrum with strongly diminishing hole density in superconducting Bi2Sr2CaCu2O8+δ . Nat. Phys. 4, 319–326 (2008).
Civelli, M., Capone, M., Kancharla, S. S., Parcollet, O. & Kotliar, G. Dynamical breakup of the Fermi surface in a doped Mott insulator. Phys. Rev. Lett. 95, 106402 (2005).
Mott, N. F. Metal-insulator transition. Rev. Mod. Phys. 40, 677–683 (1968).
Kastner, M. A., Birgeneau, R. J., Shirane, G. & Endoh, Y. Magnetic, transport, and optical properties of monolayer copper oxides. Rev. Mod. Phys. 70, 897–928 (1998).
Anisimov, V. I., Zaanen, J. & Andersen, O. K. Band theory and Mott insulators: Hubbard U instead of Stoner I. Phys. Rev. B 44, 943–954 (1991).
Acknowledgements
We thank J. Aarts, T.-M. Chuang, J. C. Davis, M. H. Hamidian, T. van Klingeren, J. Lee, M. Leeuwenhoek, V. Madhavan, F. M. Massee, K. van Oosten, J. van Ruitenbeek, S. Tewari, G. Verdoes and J. J. T. Wagenaar for valuable discussions. We acknowledge funding from the Netherlands Organization for Scientific Research (NOW/OCW) as part of the Frontiers of Nanoscience programme and the Vidi talent scheme, and from the Swiss National Science Foundation (200021-146995).
Author information
Authors and Affiliations
Contributions
I.B., K.M.B., V.F. and M.P.A. performed spectroscopic-imaging STM experiments and analysed data, E.C.H., A.d.l.T. and R.S.P. created and characterized the samples, M.P.A. supervised the study. All authors contributed to the interpretation of the data.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary information
Supplementary information (PDF 3952 kb)
Rights and permissions
About this article
Cite this article
Battisti, I., Bastiaans, K., Fedoseev, V. et al. Universality of pseudogap and emergent order in lightly doped Mott insulators. Nature Phys 13, 21–25 (2017). https://doi.org/10.1038/nphys3894
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys3894
This article is cited by
-
The emergence of global phase coherence from local pairing in underdoped cuprates
Nature Physics (2023)
-
Observation of an exotic insulator to insulator transition upon electron doping the Mott insulator CeMnAsO
Nature Communications (2023)
-
Low-energy gap emerging from confined nematic states in extremely underdoped cuprate superconductors
npj Quantum Materials (2023)
-
Unified energy law for fluctuating density wave orders in cuprate pseudogap phase
Communications Physics (2022)
-
Electronic nature of the pseudogap in electron-doped Sr2IrO4
npj Quantum Materials (2022)