Main

Consider the school teacher who is infected with influenza by a student. At some point, they may stay home from work due to the illness and a replacement instructor will fill their role. For the ill teacher, this is probably a benefit, in that they have time to recover; however, the replacement teacher is now in a social situation where infection may be much more likely. A similar narrative relates both to other essential members of society and to common situations such as asking a co-worker to attend a meeting because you have fallen ill. There is overwhelming evidence that this behavioural process occurs consistently and regularly during outbreaks. For example, numerous studies report that ∼4% of teachers are absent and have to be replaced with a substitute instructor on any given day during the influenza season in the United States of America6,7,8,9. Furthermore, ref. 7 found that teacher absenteeism peaks on the peak week of the influenza season and that vaccinating students can lower the rate of teacher absenteeism by up to 10%. For nurses tracked during the 2009 H1N1 pandemic, 24% had influenza-like-illness and 74% of these individuals stayed home from work and had to be replaced10. Clearly such relational exchange happens; nevertheless, it remains to be quantified how this behavioural process affects transmission and whether evidence exists for relational exchange in real-world outbreaks.

In its most basic form, relational exchange is defined as a node replacement process where some individuals (for example, teachers, custodians, health workers, and even children on a hockey team) will be replaced by susceptible individuals if they are ever infected. This replacement process occurs at some rate, termed γ in our equations, to account for a potential delay between when individuals become infectious and when they are diagnosed. Once replaced, a new susceptible individual is given some of the connections of the essential individual (such as students or patients). This relational exchange is important because: the new susceptible node is introduced into what is most probably a more dangerous situation with respect to disease risk; and bringing susceptible nodes from a different region of the contact network reduces the diameter of the population.

To begin, we investigated a standard mass-action model where nodes are distinguished by their state in a susceptible–infectious–recovered (SIR) model. If we do not explicitly tag nodes as being essential or non-essential, we can assume that each infectious node is replaced by a susceptible node at an effective rate γ. This simple model is described in the Methods, and always leads to smaller epidemic peaks and final epidemic sizes than the equivalent model with no relational exchange (that is, γ = 0). The logic behind this result is straightforward, essentially the system behaves like a hybrid between SIR and susceptible–infectious–susceptible (SIS) models, with an effective recovery rate equal to the sum of the recovery and relational exchange rates.

What becomes apparent is that the critical feature of relational exchange, namely that the replacement individual is put into a more dangerous situation than they were in before, is simply not captured by mass-action models. Replacement individuals are thus not equivalent to a random susceptible individual. To properly account for this effect, we introduce network structure into the population. In the network model, individuals in contact with infectious nodes will see their links rewired (the relation is exchanged) from an infectious to a susceptible node. We test a more realistic rewiring scheme through simulations in the Supplementary Information. In both the analytical analysis and the simulation models, the effect of relational exchange is simple: for every exchange the degree of the infectious node (for example, a nurse) is reduced by one, the degree of the node on the other end (for example, a patient) remains the same, and the degree of the replacement susceptible node is increased by one. Again, the events occur at a rate γ for each link with infectious nodes, and the dynamics otherwise follow the standard epidemiological model. To solve this model analytically, we can use pair approximations to describe the dynamics of both the disease and the network. To further facilitate analytic treatment, we consider the SIS model in the main text; however, qualitatively equivalent results apply to SIR models, see Fig. 1b and the Supplementary Information. The pair approximation approach consists of following the fraction of individuals that are susceptible [S] or infectious [I]

where r is the recovery rate, β is the transmission rate, and γ is the replacement rate; as well as the fraction of pairs (that is, links)

Figure 1: Analytical solutions of the relational exchange model on a network with average degree 〈k〉 = 20.
figure 1

a, Expected final epidemic size, which, unlike the classic model, can undergo either a continuous or discontinuous transition at the epidemic threshold. b, Time evolution at β/r = 0.175 for the SIS (solid lines) and SIR (dashed lines) models for both the classic model (green) and the acceleration caused by relational exchange (blue). The solid black line represents exponential growth for the SIS model. c, Illustration of the hysteresis loop that can be encountered when varying the rates at which infectious individuals are replaced.

Full size image

For relational exchange, we find both that the final epidemic size and rate of spread just before the peak can be higher, see Fig. 1. Put simply, relational exchange can parsimoniously account for faster transmission near an outbreak’s peak than would be predicted given early data on transmission. We should stress that replacement does not occur only near the peak. In the model, replacement occurs throughout the time evolution of the disease, yet we find an interesting trade-off between its early effect and its effect near the peak. This trade-off arises from the state of nodes involved in the exchanged relation; for instance, whether or not the students of the original teacher are themselves infectious. Thus, accelerating transmission is an emergent feature of relational exchange and is not due to a change in model rules. As we demonstrate with a series of agent-based models in the Supplementary Methods, accelerating transmission also occurs in considerably more complex models, including those with complex social structure, heterogeneity in contact between age groups, and empirically derived social networks.

With the form used in equations (1)–(5), our model is fully solvable. We use conservation equations for nodes, [S] + [I] = 1, and links, [SS] + [SI] + [II] = 〈k〉/2, where 〈k〉 is the average degree. This leads to a simplified system whose solution is presented in the Methods. We find that, unlike the standard SIS model on a static network, whose endemic state can only emerge via a continuous transcritical bifurcation, the endemic state in the relational exchange model can also appear through a discontinuous saddle-node bifurcation. As shown in the Methods, the transcritical bifurcation occurs when

whereas the saddle-node bifurcation, which may imply the presence of a hysteresis loop, occurs at

This analysis helps us highlight a second important feature of the model. Namely that, although the rules of the process are local, they model a global policy: the replacement rate is a function of how closely we are surveying the state of essential nodes and of how quickly we wish to replace them. However, a fast replacement rate is effective only at low prevalence, such that secondary infections because of relational exchange are rare. Now, let us assume that the replacement rate is high enough to keep an outbreak under control, but that after some time the rate is slightly reduced. This might occur, for example, after the initial fear wears off. Such a mechanism can push the system over a discontinuous transition, such that a microscopic change in γ can lead to a macroscopic change in disease prevalence. We then wish to bring the system back to its previous state, so we increase γ back to its previous value. Unfortunately, as shown in Fig. 1c, the system exhibits a hysteresis loop. The replacement rate must be increased well beyond its previous value for the system to return to the initial state.

We now turn our attention to empirical data. The question we wish to answer is whether evidence exists for relational exchange in real-world diseases. We select as our metric for relational exchange the presence of accelerating exponential transmission near the outbreak peak. This phenomenon is a ubiquitous feature of relational exchange, but very uncommon in all other general models of disease spread published to date. For this investigation, we selected two pathogens: influenza and dengue. The rationale for selecting these diseases is that they both have strong seasonality—which can drive accelerating spread in some models11,12—and have rich historical data sets. However, because dengue is a vectored pathogen, which induces a separation of timescales between transmission and behaviour, and influenza is not, we expect the importance of relational exchange to be far greater for influenza13,14,15. All models were fitted to individual seasons because both influenza and dengue lead to sterilizing immunity during a single outbreak, which is true even if there are multiple circulating strains of dengue16,17. To test for the presence of relational exchange, we fit exponential growth models to the first eight weeks of each season and then compared the predicted number of cases to the model prediction from week nine until the peak (see Methods).

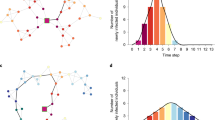
In short, we find the predicted pattern: evidence for relational exchange for influenza, but not for dengue. Figure 2 shows sixteen years of national-level influenza data from the United States of America’s Influenza-Like-Illness surveillance network. In all sixteen years, and during the 2009 pandemic, we find strong evidence that the exponential rate of transmission accelerates before the peak. For dengue, with nineteen years of data, we see only a few scattered instances of accelerating transmission–aside from the 1995 outbreak, which was the most dramatic outbreak observed since 1990.

Figure 2: Empirical evidence for relational exchange.
figure 2

a, We examined seventeen outbreaks, sixteen years and the 2009 pandemic, of national Influenza-Like-Illness (ILI) data in the USA (grey dashed lines) by fitting exponential growth models to the first eight weeks of the influenza season, defined by the USA Centers for Disease Control and Prevention (CDC) as weeks 40–20, and then comparing the observed number of cases to the exponential prediction up until the peak. For these data, ILI was defined as a fever ≥100 °F (approx. 37.778 °C) and one additional upper-respiratory symptom, for example, sore throat, during the CDC-defined influenza season without another known non-influenza cause. If more cases are reported than predicted by this exponential fit, we considered this evidence for accelerating spread and relational exchange (solid red lines). We find evidence for relational exchange in all sixteen years and during the fall wave of the 2009 pandemic. b, Example of the fitting process for a, with training data in blue and the exponential fit in solid black. c, Same analysis as in a, but for the dengue virus using nineteen years of data reported to the USA CDC in Puerto Rico, in which we found only a few isolated instances of accelerating spread. d, Example of the fitting process for c, with training data in blue and the exponential fit in solid black.

Full size image

We chose to contrast influenza and dengue precisely because both viruses are affected by seasonal forcing. The observation that influenza shows evidence for accelerating spread, and dengue largely does not, indicates that seasonal forcing alone cannot account for the observed patterns. This observed difference between dengue and influenza can parsimoniously be accounted for by relational exchange. Furthermore, existing models of influenza, even those with seasonal forcing, fail to capture the accelerating growth seen in real data13,18. For example, both papers reported evidence that absolute humidity affected the start of influenza season, more so than accelerating the rate of spread leading up to the peak, and consistently under-predicted the peak magnitude and predicted a later peak than observed. The similarity to these failed predictions and the comparison of the standard SIR model to the SIR model with relational exchange in our Fig. 2b is striking. To date, no alternative model can explain this difference, without substantially increased complexity or unrealistic assumptions. Therefore, we conclude that evidence exists for relational exchange in real-world outbreaks.

Because the Influenza-Like-Illness surveillance network is at the national level and the dengue data were the state level, we also fit the relational exchange model to state-level influenza data. Our analysis suggests that across 25 influenza seasons, and in all of the USA (we were unable to obtain data from Vermont and Alaska/Hawaii were not states during the period with historical data), greater than 70% of each season in each state (that is, >900 seasons) support relational exchange. The heatmap of the USA in Fig. 3 plots the proportion of influenza seasons between 1921 and 1951, showing evidence for relational exchange, with darker blues indicating more support than lighter blues and yellows. The data used for this analysis were not obtained from the Influenza-Like-Illness surveillance network, and were instead obtained from the USA National Notifiable Diseases Surveillance System as digitized by Project Tycho19. As a result, we now have more reliable support derived from multiple data sources and at multiple geopolitical scales, indicating that our results on relational exchange are robust to sampling errors and/or synchronization effects. We furthered evaluated the support for relational exchange by fitting models with and without relational exchange to the state-level influenza data and found strong support for the presence of relational exchange in all seasons and statistical support for the relational exchange model across more than 400 influenza outbreaks, see Supplementary Methods.

Figure 3: State-level empirical evidence for relational exchange.
figure 3

A heatmap of the USA illustrating the proportion of influenza seasons between 1921 and 1951 showing evidence for relational exchange, with darker blues indicating more support than lighter blues and yellows. On average, over 70% of seasons across all states provide support for relational exchange. The data were obtained from the USA National Notifiable Diseases Surveillance System as digitized by Project Tycho19.

Full size image

It is worth highlighting that we restricted our analysis to the USA Centers for Disease Control and Prevention influenza season and that we do find evidence for exponential growth during the first eight weeks of every influenza season, which was our training period. However, we find an even higher rate of exponential growth in the weeks leading up to the peak. Lastly, and perhaps most importantly, we see evidence for accelerating spread during the 2009 H1N1 pandemic. This pandemic occurred in the USA outside of the typical influenza season—thus probably altering any effect of seasonal forcing—and generated substantial changes in health-seeking behaviour. The fact that we still see evidence for accelerating spread during the 2009 H1N1 pandemic suggests that the mechanism must transcend seasonality and behaviours associated with health-care seeking. Relational exchange parsimoniously accounts for both seasonal and pandemic influenza. It is also worth noting that dengue and influenza do not have the same functional type of seasonal forcing. However, because dengue is also seasonally forced, this difference between the two diseases demonstrates that accelerating spread can occur with, but is not an expected consequence of, seasonal forcing. Accelerating spread is an expected consequence for relational exchange. Seasonal forcing and behaviour should thus be included and perhaps coupled for more precise predictions.

This work is not without caveats. First, in our analytical treatment, we assumed the population was infinitely large. While this is a standard assumption, clearly the model cannot be directly applied to real-world populations. Second, relational exchange modifies the degree of nodes; however, the degree distribution will never be broader than an exponential distribution, such that using a heterogeneous mean-field approach would be marginally more precise, without qualitatively changing the observed phenomena20. Third, the compartmental approach distinguishes nodes only on the basis of their state, such that while in the real world an individual might return to their past connections after recovering, our model cannot capture this behaviour, because nodes are undistinguishable. Similarly, while random rewiring increases the accuracy of compartmental models, it could also dampen the effects of relational exchange in epidemics occurring over longer timescales. Fourth, although we demonstrate that accelerating spread still occurs in age-structured populations, see Supplementary Methods, we did not use such a model to analyse the influenza and dengue time series. Future work should focus on evaluating age-structured relational exchange models with empirical data. Finally, we considered only two diseases in our empirical investigation. Future work should consider classifying a variety of different diseases, on the basis of whether they exhibit evidence for relational exchange.

There are four additional implications of this study, which will affect the broader scientific, medical, and public health communities. First, as recently demonstrated, the evolution of increased pathogen transmissibility decreases as a pathogen spreads through a heterogeneous population21. This occurs because highly connected individuals are typically infected early in an outbreak and, as these individuals recover, the epidemic potential of the population decreases22. Therefore, any process, such as relational exchange, which maintains highly connected, susceptible individuals can increase the chance of more transmissible strains evolving and persisting. Second, if individuals entering high-risk societal roles can be vaccinated or selected from resistant individuals, then relational exchange will no longer have negative effects on outbreak progression. Third, one clear prediction from this model is that replacement workers, for example, substitute teachers, may have higher rates of illness. Future work should focus on empirical studies to evaluate this prediction. Finally, methods for forecasting disease spread must include both realistic population structure and salient aspects of human behaviour. Without these key features, we cannot hope for robust, actionable models for predicting epidemics.

Methods

Mass-action compartmental approach.

We use a standard mass-action model where nodes are distinguished by their state in a SIR model (variables in brackets correspond to the fraction of the population in each state). The epidemic is described by the following system of equations,

where r is the recovery rate, β is the transmission rate, and γ is the replacement rate. All variables in brackets are dynamical, and we use the dot notation to identify time derivatives.

Network model with pair approximations.

We consider the network structure by introducing pair approximations in the SIR ordinary differential equation system

with an implicit via the conservation condition . The pairs are followed by

where all missing terms go to links involving recovered nodes (which do not need to be explicitly followed). To allow analytical treatment, we consider SIS dynamics as per equations (1)–(5) for the remainder of the analysis.

Analytical solution of the network model.

The evolution of the dynamical variables in the model is constrained by the conservation of nodes and links, which allows us to effectively reduce equations (1)–(5) to the following system of three equations:

We can readily see that a disease-free state, in which every node is susceptible,

is a steady state of the network model. To see whether there exists an endemic state in which a non-zero fraction of individuals are infectious, we set in equations (16)–(18). This yields

where we have defined the dimensionless parameters a ≡ β/r and b ≡ γ/r. Substituting these last equations in the link conservation equation, we obtain

whose solutions,

correspond to the possible values of the endemic state. The stability of the three possible steady states are obtained via a standard linear stability analysis of equations (16)–(18).

The disease-free steady state undergoes a transcritical bifurcation whenever either [I]+∗ = [I]df∗ = 0 or [I]−∗ = [I]df∗ = 0, which happens when the constant term in equation (23) equals zero.

Fixing either a or b, we find the following threshold values

Similarly, we see that the endemic steady state appears through a saddle-node bifurcation that occurs when [I]+∗ = [I]−∗ which, from equation (24), happens when

Fixing either a or b, we find the following threshold values

Notice that whenever a〈k〉 = 4, the threshold b−sn diverges, but b+sn equals −1 − 1/〈k〉(〈k〉 − 1) is always negative and therefore can be discarded. From equations (26) and (28), we see that a bistable region appears or disappears when atr = asn or btr = b±sn, which respectively yield the criteria

for the existence of a bistable region.

Empirical analysis.

For exponential growth, the corresponding equation for the number of infected individuals as a function of elapsed time is:

We estimated the parameters of both models from data using a nonlinear least squares algorithm coded in the R programming language. For both dengue and influenza we used data from the first eight weeks of each season. We further explored the sensitivity of our results to the size of the training data and found them to be robust.

Data availability.

Empirical data obtained from the USA National Notifiable Diseases Surveillance System as digitized by Project Tycho19. All other data that support the plots within this paper and other findings of this study are available from the corresponding author upon reasonable request.