Abstract
The quantum mechanical (Berry) phase of the electronic wavefunction plays a critical role in the anomalous1,2 and spin Hall effects3,4, including their quantized limits5,6,7. While progress has been made in understanding these effects in ferromagnets8, less is known in antiferromagnetic systems. Here we present a study of antiferromagnet GdPtBi, whose electronic structure is similar to that of the topologically non-trivial HgTe (refs 9,10,11), and where the Gd ions offer the possibility to tune the Berry phase via control of the spin texture. We show that this system supports an anomalous Hall angle ΘAH > 0.1, comparable to the largest observed in bulk ferromagnets12 and significantly larger than in other antiferromagnets13. Neutron scattering measurements and electronic structure calculations suggest that this effect originates from avoided crossing or Weyl points that develop near the Fermi level due to a breaking of combined time-reversal and lattice symmetries. Berry phase effects associated with such symmetry breaking have recently been explored in kagome networks14,15,16,17; our results extend this to half-Heusler systems with non-trivial band topology. The magnetic textures indicated here may also provide pathways towards realizing the topological insulating and semimetallic states9,10,11,18,19 predicted in this material class.
Similar content being viewed by others
Main
The ordinary Hall effect is due to the Lorentz force bending of charge carriers perpendicular to a magnetic field. In systems where time-reversal symmetry (TRS) is spontaneously broken, it typically can be overwhelmed by a different class of mechanisms for transverse velocity. In such systems, there are contributions to transverse velocity from both extrinsic effects due to spin-dependent scattering13 and intrinsic effects related to real space20,21 and momentum space2 Berry phase mechanisms. The former is relevant in systems with non-coplanar spin textures with finite scalar spin chirality χijk = Si ⋅ (Sj × Sk), where Sn are spins, while the latter generically occurs in TRS-broken systems originating from the spin–orbit-interaction-induced Berry curvature of the filled bands. The anomalous Hall effect (AHE) due to magnetic texture is most often associated with finite χijk and tends to exhibit relatively small anomalous Hall angles ΘAH ≲ 0.01 (such as SrFeO3 (ref. 22) or Pr2Ir2O7 (ref. 23)), while intrinsic band-structure-based effects are common in ferromagnetic systems and can be significantly larger13. Recent theoretical work has suggested that effects that rely on both magnetic texture and strong spin–orbit coupling may exist in non-collinear antiferromagnets that lead to significant Hall responses14. Single-crystal studies of Mn3Sn and Mn3Ge have been shown to support ΘAH ≲ 0.02 and 0.05, respectively, originating from its inverse triangular spin structure and electronic structure16,17.
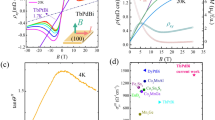
Here we study single crystals of GdPtBi, a member of the family RPtBi (R is a rare earth element) known to exhibit antiferromagnetic ordering24. As shown in Fig. 1a, this system has the half-Heusler structure consisting of interpenetrating face centred cubic (fcc) lattices of each constituent element (space group  ) with lattice constant a = 6.68 Å for R = Gd. In general, the antiferromagnetic fcc lattice is frustrated, with the Gd ions forming a triangular lattice when viewed along the 〈111〉 direction. From the high-temperature magnetic susceptibility we find a Curie–Weiss temperature θCW = −38 K, while the transition to long-range magnetic order occurs at TN = 9.2 K, as shown in Fig. 1b, consistent with previous reports24. This yields a moderate frustration parameter f ≡ − θCW/TN ∼ 4, similar to insulating fcc systems FeO and MnSe25. As shown in Fig. 1c, high-field torque magnetometry reveals a distinct kink at a magnetic field BC ≍ 25 T (seen more clearly in d2τ/dB2, which is proportional to the magnetic susceptibility), which is independent of orientation, as shown in the inset of Fig. 1c. This is suggestive of field-induced alignment of the spins and an energy scale gμBSBC = 120 K, where g = 2 is the g-factor, μB is the Bohr magneton, and S = 7/2 is the Gd spin (see Supplementary Information). This is approximately three times larger than θCW, indicating cancelling exchange interactions, as has been theoretically discussed for this material26. The structure of the magnetic ordering in B = 0 has recently been probed by X-ray and neutron scattering, which suggests an antiferromagnetic ordering (type-II) in which the Gd moments order ferromagnetically in sheets in the (111) planes, which in turn are stacked antiferromagnetically27. Theoretical work has suggested that other orderings are of comparable energy26; the structure at finite B has not been previously reported.
) with lattice constant a = 6.68 Å for R = Gd. In general, the antiferromagnetic fcc lattice is frustrated, with the Gd ions forming a triangular lattice when viewed along the 〈111〉 direction. From the high-temperature magnetic susceptibility we find a Curie–Weiss temperature θCW = −38 K, while the transition to long-range magnetic order occurs at TN = 9.2 K, as shown in Fig. 1b, consistent with previous reports24. This yields a moderate frustration parameter f ≡ − θCW/TN ∼ 4, similar to insulating fcc systems FeO and MnSe25. As shown in Fig. 1c, high-field torque magnetometry reveals a distinct kink at a magnetic field BC ≍ 25 T (seen more clearly in d2τ/dB2, which is proportional to the magnetic susceptibility), which is independent of orientation, as shown in the inset of Fig. 1c. This is suggestive of field-induced alignment of the spins and an energy scale gμBSBC = 120 K, where g = 2 is the g-factor, μB is the Bohr magneton, and S = 7/2 is the Gd spin (see Supplementary Information). This is approximately three times larger than θCW, indicating cancelling exchange interactions, as has been theoretically discussed for this material26. The structure of the magnetic ordering in B = 0 has recently been probed by X-ray and neutron scattering, which suggests an antiferromagnetic ordering (type-II) in which the Gd moments order ferromagnetically in sheets in the (111) planes, which in turn are stacked antiferromagnetically27. Theoretical work has suggested that other orderings are of comparable energy26; the structure at finite B has not been previously reported.
a, Crystal structure of GdPtBi, consisting of three interpenetrating fcc lattices with lattice constant a = 6.68 Å. The spin direction for Gd in the antiferromagnetic phase is shown. b, Resistivity ρ and magnetic susceptibility M/H for a magnetic field B along the [001] direction as a function of temperature T through the antiferromagnetic transition temperature TN = 9.2 K. B = 0.01 T is applied for the measurement of M/H. c, Magnetic torque measured to B = 31 T (blue line). The geometry of field and crystal is shown in the inset. The second derivative d2τ/dB2 (also shown in main panel, red line) shows a sharp change near B = 25 T that is independent of orientation (shown in the upper inset).
The focus of the present study is the interplay of the magnetic structure and strong spin–orbit coupling in GdPtBi. The heavy-element PtBi sublattice is expected to provide the system with a similar electronic structure to that of HgTe (refs 9,10,11), sensitive to the magnetic ordering of the Gd ions through the spin–orbit interaction. The bulk electronic structure of GdPtBi is known to be semimetallic28. As shown in Fig. 1b, the observed resistivity as a function of temperature ρ(T) has a moderate increase with decreasing T, while at low temperature it shows a clear kink concomitant with the magnetic transition at TN. A richer perspective of the coupling of the conduction electrons to the magnetic order is provided by magnetotransport. The longitudinal resistivity as a function of magnetic field ρxx(B), with B along the [001] direction, is shown in Fig. 2a. At temperatures T > TN we observe an approximately quadratic dependence on B, indicating an average mobility μavg ≍ 1,000 cm2 V−1 s−1. As T is lowered, we observe a dip in ρxx that develops near B = 4 T, progressively deepening to T = 2.5 K. Measurements to B = 31 T (see Supplementary Information) show that this is not related to Landau quantization, as no continued pattern in B−1 connected to this feature is observed with the appearance of Shubnikov–de Haas (SdH) oscillations for B > 10 T.
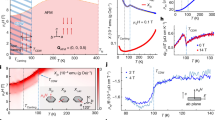
a, Longitudinal resistivity as a function of B along [001]. b, Transverse resistivity as a function of B along [001]. c, Magnetization as a function of B along [001]. d, Integrated Gaussian area G of (0.5 0.5 2.5) and (111) Bragg peaks, proportional to the square of the sublattice magnetization and bulk magnetization, respectively, measured using neutron scattering as a function of B applied along [1 0] at T = 2 K. The square of M at T = 2 K is also plotted. Error bars indicate the standard error. e, Anomalous Hall angle Δσxy/σxx as a function of temperature.
0] at T = 2 K. The square of M at T = 2 K is also plotted. Error bars indicate the standard error. e, Anomalous Hall angle Δσxy/σxx as a function of temperature.
The field dependence of the transverse resistivity ρyx(B) is shown in Fig. 2b. At T = 50 K we see a Hall effect consistent with multiband conduction, as would be expected from the electronic structure28. Upon lowering T, we see a prominent feature develop in the vicinity of B = 4 T, which corresponds to an enhancement in ρyx of 55% at T = 2.5 K. This feature draws a distinct contrast with the magnetization M. As shown in Fig. 2c, for T both above and below TN, we see an approximately linear and featureless M(B). In magnetic systems, it is conventional to describe three separate contributions to ρyx = R0B + RSM + ρyxT, where R0 is the ordinary Hall coefficient, RS is the anomalous Hall coefficient coupled to M, and ρyxT is the Hall effect arising from spin textures. As described above, the final among these include non-coplanar textures that generate finite χijk (refs 29,30,31) as well as non-collinear textures that allow finite momentum-space Berry curvature14,15,16,17. Structure in ρyx(B) from Berry phase effects normally mirrors that in M unless there are contributions related to spin texture. Mathematical separation of these components is often performed in the literature to isolate ρyxT (ref. 32). Performing such analysis we estimate ρyxT = 0.18 mΩ cm (see Supplementary Information), significantly larger than has been previously reported in any antiferromagnetic system, both in terms of absolute value and size relative to ρxx (see Supplementary Information). We note that the empirical relationship used for additivity of the contributions to ρyx is valid only in the limit of small Hall angle, whereas at all values of the Hall angle it is possible to discuss additivity in the transverse conductivity σxy. Here we quantify the AHE using the anomalous Hall angle ΘAH = σxyA/σxx = (σxy − σxyN)/σxx, where A(N) denotes the anomalous (normal) part of the Hall conductivity. We estimate σxyN by using σxy(T = 50 K), which is far above TN and reflects the ordinary contribution to the Hall effect, and refer to the resulting anomalous Hall contribution as Δσxy, as shown in Fig. 2e (similar behaviour is obtained by fitting the σxyN at large B). The value of ΘAH peaks at more than 0.15 at B = 4 T, which is larger than has been previously observed in antiferromagnetic systems. A view of this transport response in the space of B and T is shown in Fig. 3a. The region with the largest Δσxy, corresponding to the peak feature we observe, occurs near B = 4 T and below TN = 9.2 K. However, the anomalous Hall response persists to significantly higher temperatures, with a reduced magnitude, finally disappearing between 25 and 30 K.
a, Colour plot of Δσxy for T between 2 K and 50 K and B from 0 to 14 T. b, Scaling of the anomalous Hall conductivity Δσxy as a function of σxx for five different single crystals. The straight line is a fit to the power-law Δσxy ∝ σxxα. c, Temperature dependence of the scaling power-law α. Error bars indicate the standard error.
The most common contribution of magnetic texture to the AHE is that of finite χijk appearing in systems that have skyrmionic spin textures stabilized by the Dzyaloshinskii–Moriya interaction30,31. It has also been recognized that frustrated magnets may play host to similar texture-induced Hall effects23. More recently, theoretical work has suggested that, in antiferromagnets, a band-structure-induced intrinsic AHE may arise in the presence of non-collinear spin structures that break the combined time-reversal and lattice symmetries of the simple antiferromagnetic state14. Such a situation is realized in GdPtBi as the B = 0 type-II antiferromagnetic spin structure cants in finite B. Neutron scattering measurements confirm both the type-II ordering in fields up to 10 T (see Supplementary Information) and a ferromagnetic canting, as evidenced by an increase in intensity at the nuclear Bragg positions with increasing B, as shown for (111) in Fig. 2d along with its scaling with M2. Additionally, an applied field produces an enhancement in the magnetic Bragg peaks, as shown for (0.5 0.5 2.5) in Fig. 2d, which saturates above 6 T, similar to the field scale for disappearance of the anomalous Hall response. For antiferromagnetic systems with such broken time-reversal and lattice symmetries and large spin–orbit coupling, the anomalous Hall response is predicted to be significant—calculated to be 218 Ω−1 cm−1 for Mn3Ir (ref. 14). The variation of the Hall response across five different GdPtBi crystals is shown in Fig. 3b; the observed Δσxy = 30–200 Ω−1 cm−1 are comparable to that predicted for the intrinsic AHE case. We note that the transport observations also parallel predictions for the distorted fcc lattice with finite orbital magnetization33. However, this requires the presence of a type-I magnetic ordering and finite χijk, which is inconsistent with our neutron scattering measurements (see Supplementary Information).
In terms of scaling of the AHE, we find a temperature-dependent scaling factor α (defined as Δσxy ∼ σxxα), as shown in Fig. 3c. At low T, we find α = 1.2, intermediate between the value of 1.6 expected for the intrinsic AHE in multiband disordered metals34,35 and the σxx-invariant intrinsic AHE in moderately clean systems. This crossover is predicted to occur in ferromagnets in the vicinity of σxx ∼ 103 Ω−1 cm−1, similar to the scale observed here. The existence of frustrated magnetic interactions in GdPtBi, as shown by the moderate value of f, suggests that short-range correlations persist above TN (ref. 26); such correlations in the absence of long-range order have been shown to affect transport in PdCrO2 (ref. 36) and Pr2Ir2O7 (ref. 23). We hypothesize that this extends to the anomalous Hall effect observed here, as such fluctuations will break the same symmetry as the ordered phase, which is distinct from that expected for Mn3Ge and Mn3Sn, where fluctuations due to symmetric exchange cancel (see Supplementary Information).
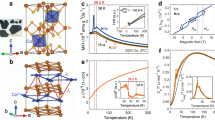
To investigate the origin of the large AHE allowed in GdPtBi in finite B, we consider the effect of the spin texture on the electronic structure. Band-touching points in the bulk electronic structure of GdPtBi have been previously reported in calculations with an uncanted magnetic structure37 which, if driven to anticrossings near the Fermi level, could be a source of significant AHE as in ferromagnetic systems35. We have performed electronic structure calculations for magnetically ordered GdPtBi using the rhombohedral magnetic unit cell shown in Fig. 4a. The approximate location of EF is determined from the ordinary Hall effect and kF from SdH oscillations (see Supplementary Information), and the B dependence of the spin structure is calculated using the results of the magnetic and neutron scattering experiments. For B = 0 we find that the type-II ordered system exhibits band touching at Γ, as shown in Fig. 4b. The structures with spin canting for B = 4 T and 8 T along the [001] direction are shown in Fig. 4c and d, respectively. The bands near the Fermi level originate from Pt and Bi (see Supplementary Information). The combination of the large spin–orbit coupling and critical band alignment of the system amplifies the physical consequence of the Gd spin texture on these bands; inspection of the band structure shows the development of avoided crossings near EF which carry significant Berry curvature. This suggests that the evolution of the electronic structure due to spin texture will generate significant Berry phase contributions to the AHE. The requirement that the combined symmetry of the antiferromagnetic state be broken to observe the AHE necessitates the application of finite B (ref. 14)—the calculations here indicate that the particularly large response relies on the detailed band structure of GdPtBi itself. We note that Weyl points have been predicted to appear in the electronic structure of the HgTe class compounds18, and can be a source of significant anomalous Hall conductivity15,16,38. While such points do not appear along the high-symmetry directions in the calculated structure, here they may be expected to appear at other points in momentum space39. If sufficiently isolated Weyl points exist near EF, they may also contribute to the AHE in a manner similar to avoided crossings (magnetotransport possibly indicative of Weyl points is observed in these crystals as shown in the Supplementary Information). Further theoretical work is needed to determine if such conditions are met in GdPtBi. More broadly, the symmetry-allowed momentum-space Berry phase mechanism provides a consistent description for the transport, scattering and calculation results presented herein.
a, Rhombohedral magnetic unit cell for type-II magnetically ordered GdPtBi. b, Electronic structure without an external magnetic field. c,d, Electronic structure for canted type-II magnetic order in the presence of applied magnetic fields B = 4 T and 8 T, respectively, applied along the [001] direction.
It has been predicted that spin–orbit-driven band inversion in the bulk of RPtBi may give rise to a topological insulating state9,10,11, although thus far experiments using photoemission to probe the band structure have been unable to resolve the topological nature of the surface bands28. The symmetry-broken ground states known to occur in RPtBi are then of heightened interest, as they would be projected on to a potentially topologically non-trivial ground state. The evolution of the bulk band structure is relevant to the AHE presented here; the band topology of RPtBi provides a band structure acutely sensitive to gap formation via the magnetic texture and strong spin–orbit coupling of the system. Additionally, the antiferromagnetic ordering itself has been predicted to give rise to a new type of topological insulating state where a combined time-reversal and translational symmetry is the source of protection for the surface modes19, a scenario further enriched by the observations here. This highlights GdPtBi as a candidate platform not only for hosting topological edge modes in the antiferromagnetic state19, but also as a novel TRS-broken topological insulator with non-collinear spin texture in finite B (ref. 6).
The combination of spin–orbit and correlation effects is expected to reveal new behaviour beyond that possible for single-electron physics. Here, the combination of strong spin–orbit coupling and symmetry breaking probed by neutron scattering gives rise to an extremely large anomalous Hall response that connects to recent theories for emerging effects in antiferromagnetic systems14 and the calculated electron structure. This effect and its scaling with conductivity12 provide an antiferromagnetic example to generalize the notion of phase-space Berry phase effects in TRS-broken systems40. Furthermore, it provides an example of a robust AHE driven by the combined role of spin–orbit coupling and spin texture that demonstrates the ubiquity of the Berry phase mechanism in symmetry-broken systems.
Methods
Single crystals of GdPtBi were grown using a flux method following ref. 24. A mixture of 99.99% Pt wire, 99.9% pure Gd, and 99.999% Bi needles in a molar ratio of 1:1:20 was put in an alumina crucible and sealed in an evacuated quartz tube with 0.016 MPa Argon gas. The sample was heated at 1,100 °C for 2 h and then cooled slowly between 900 °C and 600 °C at a rate of 2 °C h−1, followed by centrifuging to dissociate the GdPtBi crystals from the Bi flux. For neutron scattering experiments, 97.7% isotope-enriched 160Gd (with a purity of 99.9%) was used. All the obtained crystals were confirmed to be of single phase by a powder X-ray diffraction method. The crystals were aligned by X-ray Laue back-reflection and/or single-crystal X-ray diffraction techniques. Transport measurements were performed with a conventional four-probe method. To correct for contact misalignment, the measured longitudinal and transverse voltages were field symmetrized and antisymmetrized, respectively. Magnetization measurements were performed using a commercial superconducting quantum interference device (SQUID) magnetometer. Torque magnetometry was performed using a BeCu cantilever, with the deflection detected by a capacitance bridge. Neutron scattering measurements were carried out on the triple-axis spectrometer BT-7 at the NIST Center for Neutron Research41. Electronic structure calculations were performed using the projector augmented wave method and exchange–correlation potential with the generalized gradient approximation of Perdew–Burke–Ernzerhof parameters, implemented in the Vienna ab initio simulation package42.
Data availability.
The data that support the plots within this paper and other findings of this study are available from the corresponding author upon reasonable request.
References
Karplus, R. & Luttinger, J. M. Hall effect in ferromagnetics. Phys. Rev. 95, 1154–1160 (1954).
Haldane, F. D. M. Berry curvature on the Fermi surface: anomalous Hall effect as a topological Fermi-liquid property. Phys. Rev. Lett. 93, 206602 (2004).
Murakami, S., Nagaosa, N. & Zhang, S.-C. Dissipationless quantum spin current at room temperature. Science 301, 1348–1351 (2003).
Sinova, J. et al. Universal intrinsic spin Hall effect. Phys. Rev. Lett. 92, 126603 (2004).
Yu, R. et al. Quantized anomalous Hall effect in magnetic topological insulators. Science 329, 61–64 (2010).
Nomura, K. & Nagaosa, N. Surface-quantized anomalous Hall current and the magnetoelectric effect in magnetically disordered topological insulators. Phys. Rev. Lett. 106, 166802 (2011).
Kane, C. L. & Mele, E. J. Z2 topological order and the quantum spin Hall effect. Phys. Rev. Lett. 95, 146802 (2005).
Xiao, D., Chang, M.-C. & Niu, Q. Berry phase effects on electronic properties. Rev. Mod. Phys. 82, 1959–2007 (2010).
Chadov, S. et al. Tunable multifunctional topological insulators in ternary Heusler compounds. Nature Mater. 9, 541–545 (2010).
Lin, H. et al. Half-Heusler ternary compounds as new multifunctional experimental platforms for topological quantum phenomena. Nature Mater. 9, 546–549 (2010).
Xiao, D. et al. Half-Heusler compounds as a new class of three-dimensional topological insulators. Phys. Rev. Lett. 105, 096404 (2010).
Onoda, S., Sugimoto, N. & Nagaosa, N. Quantum transport theory of anomalous electric, thermoelectric, and thermal Hall effects in ferromagnets. Phys. Rev. B 77, 165103 (2008).
Nagaosa, N., Sinova, J., Onoda, S., MacDonald, A. H. & Ong, N. P. Anomalous Hall effect. Rev. Mod. Phys. 82, 1539–1592 (2010).
Chen, H., Niu, Q. & MacDonald, A. H. Anomalous Hall effect arising from noncollinear antiferromagnetism. Phys. Rev. Lett. 112, 017205 (2014).
Kubler, J. & Felser, C. Non-collinear antiferromagnets and the anomalous Hall effect. Europhys. Lett. 108, 67001 (2014).
Nakatsuji, S., Kiyohara, N. & Higo, T. Large anomalous Hall effect in a non-collinear antiferromagnet at room temperature. Nature 527, 212–215 (2015).
Nayak, A. K. et al. Large anomalous Hall effect driven by a nonvanishing Berry curvature in the noncolinear antiferromagnet Mn3Ge. Sci. Adv. 2, e1501870 (2016).
Ruan, J. et al. Symmetry-protected ideal Weyl semimetal in HgTe-class materials. Nature Commun. 7, 11136 (2016).
Mong, R. S. K., Essin, A. M. & Moore, J. E. Antiferromagnetic topological insulators. Phys. Rev. B 81, 245209 (2010).
Ohgushi, K., Murakami, S. & Nagaosa, N. Spin anisotropy and quantum Hall effect in the kagome lattice: chiral spin state based on a ferromagnet. Phys. Rev. B 62, R6065 (2000).
Matl, P. et al. Hall effect of the colossal magnetoresistance manganite La1−xCaxMnO3 . Phys. Rev. B 57, 10248–10251 (1998).
Ishiwata, S. et al. Versatile helimagnetic phases under magnetic fields in cubic perovskite SrFeO3 . Phys. Rev. B 84, 054427 (2011).
Machida, Y. et al. Unconventional anomalous Hall effect enhanced by a noncoplanar spin texture in the frustrated Kondo lattice Pr2Ir2O7 . Phys. Rev. Lett. 98, 057203 (2007).
Canfield, P. C. et al. Magnetism and heavy fermion-like behavior in the RBiPt series. J. Appl. Phys. 70, 5800–5802 (1991).
Ramirez, A. P. Strongly geometrically frustrated magnets. Annu. Rev. Mater. Sci. 24, 453–480 (1994).
Khmelevskyi, S. Antiferromagnetic ordering on the frustrated fcc lattice in the intermetallic compound GdPtBi. Phys. Rev. B 86, 104429 (2012).
Kreyssig, A. et al. Magnetic order in GdBiPt studied by X-ray resonant magnetic scattering. Phys. Rev. B 84, 220408 (2011).
Liu, C. et al. Metallic surface electronic state in half-Heusler compounds RPtBi (R = Lu, Dy, Gd). Phys. Rev. B 83, 205133 (2011).
Taguchi, Y., Oohara, Y., Yoshizawa, H., Nagaosa, N. & Tokura, Y. Spin chirality, Berry phase, and anomalous Hall effect in a frustrated ferromagnet. Science 291, 2573–2576 (2001).
Lee, M., Kang, W., Onose, Y., Tokura, Y. & Ong, N. P. Unusual Hall effect anomaly in MnSi under pressure. Phys. Rev. Lett. 102, 186601 (2009).
Neubauer, A. et al. Topological Hall effect in the A phase of MnSi. Phys. Rev. Lett. 102, 186602 (2009).
Li, Y. et al. Robust formation of skyrmions and topological Hall effect anomaly in epitaxial thin films of MnSi. Phys. Rev. Lett. 110, 117202 (2013).
Shindou, R. & Nagaosa, N. Orbital ferromagnetism and anomalous Hall effect in antiferromagnets on the distorted fcc lattice. Phys. Rev. Lett. 87, 116801 (2001).
Branford, W. R. et al. Coexistence of universal and topological anomalous Hall effects in metal CrO2 thin films in the dirty limit. Phys. Rev. Lett. 102, 227201 (2009).
Onoda, S., Sugimoto, N. & Nagaosa, N. Intrinsic versus extrinsic anomalous Hall effect in ferromagnets. Phys. Rev. Lett. 97, 126602 (2006).
Daou, R., Fresard, R., Hebert, S. & Maignan, A. Impact of short-range order on transport properties of the two-dimensional metal PdCrO2 . Phys. Rev. B 92, 245115 (2015).
Li, Z., Su, H., Yang, X. & Zhang, J. Electronic structure of the antiferromagnetic topological insulator candidate GdBiPt. Phys. Rev. B 91, 235128 (2015).
Moon, E.-G., Xu, C., Kim, Y. B. & Balents, L. Non-Fermi-liquid and topological states with strong spin–orbit coupling. Phys. Rev. Lett. 111, 206401 (2013).
Witczak-Krempa, W. & Kim, Y. B. Topological and magnetic phases of interacting electrons in the pyrochlore iridates. Phys. Rev. B 85, 045124 (2012).
Freimuth, F., Bamler, R., Mokrousov, Y. & Rosch, A. Phase-space Berry phases in chiral magnets: Dzyaloshinskii–Moriya interaction and the charge of skyrmions. Phys. Rev. B 88, 214409 (2013).
Lynn, J. W. et al. Double-focusing thermal triple-axis spectrometer at NCNR. J. Res. Natl Inst. Stand. Technol. 117, 61–79 (2012).
Kresse, G. & Furthmuller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186 (1996).
Acknowledgements
We are grateful to Y. Lee, L. Fu, L. Savary and H. Sakai for fruitful discussions. This research is funded in part by the Gordon and Betty Moore Foundation EPiQS Initiative, Grant GBMF3848 to J.G.C., material development by NSF grant DMR-1554891, and instrumentation development with ARO grant W911NF-16-1-0034. W.F. acknowledges support from the NSF of China (No. 11374033). D.X. acknowledges support from DOE Basic Energy Sciences Grant No. DE-SC0012509. A.D. acknowledges support by the STC Center for Integrated Quantum Materials, NSF Grant No. DMR-1231319. J.G.C. acknowledges support from the Bose Fellows Program at MIT. A portion of this work was performed at the National High Magnetic Field Laboratory, which is supported by National Science Foundation Cooperative Agreement No. DMR-1157490, the State of Florida, and the US Department of Energy. We acknowledge the National Institute of Standards and Technology, US Department of Commerce, in providing the BT-7 neutron facility used in this work.
Author information
Authors and Affiliations
Contributions
T.S. and Y.-T.L. synthesized the crystals. T.S., A.D. and Y.-T.L. performed the electrical measurements. T.S., R.C. and J.W.L. performed the neutron scattering experiments. W.F. and D.X. performed the electronic structure calculations. All authors participated in discussion of the results and writing the paper. J.G.C. coordinated the project.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary information
Supplementary information (PDF 3410 kb)
Rights and permissions
About this article
Cite this article
Suzuki, T., Chisnell, R., Devarakonda, A. et al. Large anomalous Hall effect in a half-Heusler antiferromagnet. Nature Phys 12, 1119–1123 (2016). https://doi.org/10.1038/nphys3831
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys3831
This article is cited by
-
The discovery of three-dimensional Van Hove singularity
Nature Communications (2024)
-
Large anomalous Hall effect and negative magnetoresistance in half-topological semimetals
Communications Physics (2023)
-
Emergence of Weyl fermions by ferrimagnetism in a noncentrosymmetric magnetic Weyl semimetal
Nature Communications (2023)
-
Rational design of large anomalous Nernst effect in Dirac semimetals
npj Computational Materials (2023)
-
Topological Lifshitz transition and one-dimensional Weyl mode in HfTe5
Nature Materials (2023)