Abstract
One of the key challenges in spectroscopy is the inhomogeneous broadening that masks the homogeneous spectral lineshape and the underlying coherent dynamics. Techniques such as four-wave mixing and spectral hole-burning are used in optical spectroscopy1,2,3, and spin-echo4 in nuclear magnetic resonance (NMR). However, the high-power pulses used in spin-echo and other sequences4,5,6,7,8 often create spurious dynamics7,8 obscuring the subtle spin correlations important for quantum technologies5,6,9,10,11,12,13,14,15,16,17. Here we develop NMR techniques to probe the correlation times of the fluctuations in a nuclear spin bath of individual quantum dots, using frequency-comb excitation, allowing for the homogeneous NMR lineshapes to be measured without high-power pulses. We find nuclear spin correlation times exceeding one second in self-assembled InGaAs quantum dots—four orders of magnitude longer than in strain-free III–V semiconductors. This observed freezing of the nuclear spin fluctuations suggests ways of designing quantum dot spin qubits with a well-understood, highly stable nuclear spin bath.
Similar content being viewed by others
Main
Pulsed magnetic resonance is a diverse toolkit with applications in chemistry, biology and physics. In quantum information applications, solid state spin qubits are of great interest and are often described by the so-called central spin model, where the qubit (central spin) is coupled to a fluctuating spin bath (typically interacting nuclear spins). Here microwave and radiofrequency (rf) magnetic resonance pulses are used for the initialization and readout of a qubit18, dynamical decoupling5 and dynamic control6 of the spin bath.
However, the most important parameter controlling the central spin coherence9,11,19—the correlation time τc of the spin bath fluctuations—is very difficult to measure directly. The value of τc is determined by the spin exchange (flip-flops) of the interacting nuclear bath spins. By contrast, pulsed NMR reveals the spin bath coherence time T2, which characterizes the dynamics of the transverse nuclear magnetization7,8,20 and is much shorter than τc. The problem is further exacerbated in self-assembled quantum dots, where quadrupolar effects lead to inhomogeneous NMR broadening exceeding 10 MHz (refs 21,22), so that pulsed NMR requires practically unattainable rf field amplitudes exceeding 1 T.
Here we develop an alternative approach to NMR spectroscopy: we measure non-coherent depolarization of nuclear spins under weak noise-like rf fields. Contrary to intuitive expectation, we show that such measurement can reveal the full homogeneous NMR lineshape describing the coherent spin dynamics. This is achieved by employing rf excitation with a frequency-comb profile (widely used in precision optical metrology23). We then exploit non-resonant nuclear–nuclear interactions: the homogeneous NMR lineshape of one isotope measured with frequency-comb NMR is used as a sensitive non-invasive probe of the correlation times τc of the nuclear flip-flops of the other isotope. Although initial studies9,17,19 suggested τc ∼ 100 μs for nuclear spins in III–V semiconductors, it was recently recognized20,24,25 that quadrupolar effects may have a significant impact in self-assembled quantum dots. Here, for the first time, we obtain a quantitative measurement of extremely long τc ≳ 1 s, revealing strong freezing of the nuclear spin bath due to the inhomogeneous strain—a crucial advantage for quantum information applications of self-assembled quantum dots.
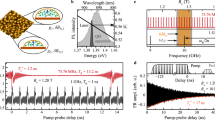
The experiments were performed on individual neutral self-assembled InGaAs/GaAs quantum dots at magnetic field Bz = 8 T. All measurements of the nuclear spin depolarization dynamics employ the pump-depolarize-probe protocol shown in Fig. 1a. Here we exploit the hyperfine interaction of the nuclei with the optically excited electron17,21,22 both to polarize the nuclei (pump pulse) and to measure the nuclear spin polarization in terms of the Overhauser shift ΔEhf in the quantum dot photoluminescence spectrum (probe pulse). The rf magnetic field depolarizing nuclear spins is induced by a small copper coil. (Further experimental details can be found in Methods and Supplementary Note 1.)
a, Timing diagram of the experimental cycle consisting of nuclear spin optical pumping (duration tpump), frequency-comb rf excitation (trf), and optical probing of the nuclear spin state (tprobe). b, The green line shows schematically a quantum dot NMR spectrum consisting of a central transition (CT) peak and two satellite transition (ST) bands. The inhomogeneous lineshape (width Δνinh) is the sum of a large number (104–105) of nuclear spin transitions with homogeneous linewidths Δνhom (shown with red lines). The black line shows the spectrum of the frequency-comb excitation with mode spacing fMS and total width Δνcomb exceeding Δνinh. c,d, Demonstrate how experiments with varying fMS can reveal the width Δνhom of the NMR homogeneous lineshape (red lines). When Δνhom > fMS (c), all individual nuclei are uniformly excited by the frequency comb (shown with black lines). In the opposite case Δνhom < fMS (d), some of the nuclei (dashed line) are not excited, resulting in a slow-down of nuclear spin dynamics. The transition between the two cases takes place when fMS ∼ Δνhom, allowing Δνhom to be measured.
All isotopes in the studied dots possess non-zero quadrupolar moments. Here we focus on the spin I = 3/2 nuclei 71Ga and 75As. The strain-induced quadrupolar shifts result in an inhomogeneously broadened NMR spectrum21,22, as shown schematically by the green line in Fig. 1b. The spectrum consists of a central transition (CT) −1/2 ↔ +1/2 and two satellite transition (ST) ±1/2 ↔ ±3/2 peaks. All nuclei in the dot are coupled by dipole–dipole interactions: an exact description of such a system is a very complex many-body quantum mechanical problem. Here we use a simplified semiclassical description where nuclear–nuclear interactions are taken into account by introducing a phenomenological homogeneous broadening of each nuclear spin transition. Thus, the NMR spectrum in Fig. 1b is an inhomogeneous distribution (with width Δνinh) of individual nuclear spin transitions (shown by the red lines) with much smaller homogeneous linewidth Δνhom.
Radiofrequency excitation is considered to be weak when nuclear spin precession is slower than transverse relaxation, resulting in non-coherent depolarization (that is without Rabi oscillations) of the nuclei26. To make such depolarization sensitive to the homogeneous NMR lineshape, we use rf excitation with a frequency-comb spectral profile. As shown in Fig. 1b (black line), the frequency comb has a mode spacing of fMS and a total comb width Δνcomb exceeding Δνinh. The key idea of the frequency-comb technique is described in Fig. 1c, d, where two possible cases are shown. If the spacing is small (fMS ≪ Δνhom, Fig. 1c) all nuclear transitions are excited by a large number of rf modes. As a result, all nuclear spins are depolarized at the same rate and we expect an exponential decay of the total nuclear spin polarization. In the opposite case of large mode separation (fMS > Δνhom, Fig. 1d), some of the nuclear transitions are out of resonance and are not excited (for example, the one shown by the dashed red line). As a result we expect a slowed-down non-exponential nuclear depolarization. The experiments are performed at different fMS; the fMS for which a slow-down in depolarization is observed gives a measure of the homogeneous linewidth Δνhom.
Experimental demonstration of this technique is shown in Fig. 2a. The Overhauser shift variation ΔEhf of 71Ga is shown as a function of the depolarizing rf pulse duration trf for different fMS. For small values of fMS = 80 and 435 Hz an exponential depolarization is observed. However, when fMS is increased the depolarization becomes non-exponential and slows down significantly. The detailed dependence ΔEhf(trf, fMS) is shown as a colour-coded plot in Fig. 2b. The threshold value of fMS (marked with a white arrow) above which the nuclear spin dynamics becomes sensitive to the discrete structure of the frequency comb provides an estimate of Δνhom ∼ 450 Hz. Such a small homogeneous linewidth is detected in NMR resonances with inhomogeneous broadening of Δνinh ∼ 6 MHz (ref. 21), demonstrating the resolution power of frequency-comb non-coherent spectroscopy.
a, The change in the polarization of the 71Ga nuclear spins (measured in terms of the change in the Overhauser shift ΔEhf) is shown as a function of the rf pulse duration trf (symbols) at Bz = 8 T and different mode spacings fMS. Lines show model fitting (see text). b, A full 2D plot of ΔEhf as a function of trf and fMS in the same experiment as in a. There is a clear slow-down of the nuclear spin depolarization at fMS > 450 Hz (shown with a white arrow), providing an estimate of the homogeneous linewidth of Δνhom.
The information revealed by frequency-comb spectroscopy is not limited to rough estimates. An accurate determination of the linewidth and the shape of the tails of the full homogeneous lineshape is achieved with spin dynamics modelling based on rate equations (see details in Methods and Supplementary Note 2). We use the following two-parameter phenomenological model for the homogeneous lineshape:

where Δνhom is the homogeneous full-width at half-maximum and k is a roll-off parameter that controls the tails (the behaviour of L(ν) at large ν). For k = 1 the lineshape corresponds to Lorentzian, whereas for k → ∞ it tends to Gaussian: in this way equation (1) seamlessly describes the two most common lineshapes. Using Δνhom and k as parameters we calculate the model ΔEhf(trf, fMS) dependence and fit it to the experimental ΔEhf(trf, fMS) to find a phenomenological description of the homogeneous NMR lineshape in self-assembled quantum dots.
The solid line in Fig. 3a shows the best-fit lineshape (Δνhom ≍ 221 Hz and k ≍ 1.67) for the measurement shown in Fig. 2a, b. The dashed and dashed-dotted lines in Fig. 3a show for comparison the Lorentzian (k = 1) and Gaussian (k → ∞) lineshapes with the same Δνhom. The difference in the lineshape tails is seen clearly in Fig. 3b, where a logarithmic scale is used. The model ΔEhf(trf, fMS) dependence calculated with the best-fit parameters is shown in Fig. 3c and with lines in Fig. 2a—there is excellent agreement with experiment. By contrast, modelling ΔEhf(trf, fMS) with Lorentzian (Fig. 3d) and Gaussian (Fig. 3e) lineshapes shows a pronounced deviation from the experiment, demonstrating the excellent sensitivity of the frequency-comb spectroscopy to the tails of the homogeneous spectral lineshape.
a,b, Model homogeneous NMR lineshapes of 71Ga nuclei shown on linear (a) and logarithmic (b) scales. Solid lines show the best-fit lineshape with a full-width at half-maximum Δνhom ≍ 221 Hz and a roll-off parameter k ≍ 1.67. Dashed and dashed-dotted lines show for comparison Lorentzian and Gaussian lineshapes with the same Δνhom. c–e, The calculated ΔEhf(trf, fMS) dependences for the lineshapes in a,b. For the fitted lineshape (c) an excellent agreement with the experiment in Fig. 2b is found, whereas calculations with Lorentzian (d) and Gaussian (e) lineshapes give markedly different results, demonstrating the sensitivity of the frequency-comb technique.
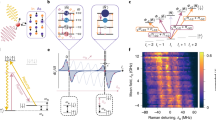
We have also performed frequency-comb NMR spectroscopy on 75As nuclei (Fig. 4a). Despite their larger inhomogeneous broadening, Δνinh ∼ 18 MHz, the model fitting reveals even smaller Δνhom ≍ 117 Hz and k ≍ 1.78. From the Δνhom derived here we can estimate the nuclear spin coherence times T2 ≍ 1/(πΔνhom) ∼ 1.4 and 2.7 ms for 71Ga and 75As, respectively. These values are in good agreement with the corresponding spin-echo T2 ≍ 1.2 and 4.3 ms derived in ref. 20. However, spin-echo could be measured only on the central transitions, for which Δνinh is relatively small. Moreover, pulsed NMR does not allow determination of the full homogeneous lineshape, which for dipole–dipole interactions typically has a ‘top-hat’-like (Gaussian) profile27. And, most importantly, owing to parasitic effects such as ‘instantaneous diffusion’7 and spin locking8, pulsed NMR does not reveal the characteristic correlation time τc of the spin exchange flip-flops. In particular, owing to the ‘instantaneous diffusion’, the slow flip-flop dynamics become obscured by the much faster and trivial spin dynamics arising from a combined effect of secular spin–spin interactions and strong rf pulses7.
a,b, Frequency-comb measurement on 75As nuclei at Bz = 8 T without (a) and with (b) additional frequency-comb excitation ‘heating’ the 71Ga nuclei. The increase of Δνhom of 75As under the 71Ga ‘heating’ reveals the strongly suppressed nuclear spin fluctuations of 71Ga. c,d, Symbols show rf-induced depolarization time τAs of 75As nuclei at fixed fMS = 903 Hz and four different amplitudes of the 75As comb β1, As as a function of the amplitude β1, Ga of the additional rf excitation ‘heating’ either the central transition (CT, c) or the satellite transition (ST, d) of 71Ga. Error bars show 95% confidence intervals. The top scales show β1, Ga expressed in terms of the rf-induced spin-flip time τGa of 71Ga. The lines show model fitting from which we deduce the 71Ga nuclear spin correlation times τc, CT ≍ 1.0 ± 0.2 s and τc, ST ≍ 6.2 ± 2.5 s for the CT and ST transitions.
As we now show, the non-Gaussian lineshapes can be understood and τc can be derived using experiments with two frequency combs exciting nuclei of two isotopes (75As and 71Ga). We again excite 75As nuclei with a frequency comb to measure their homogeneous lineshape. The difference is that now we simultaneously apply a second comb exciting the 71Ga spins. Importantly, in this experiment the 71Ga nuclei are first fully depolarized after the optical nuclear spin pumping and before the two-comb excitation (see Supplementary Fig. 3)—in this way the excitation of 71Ga has no direct effect on the measured hyperfine shift ΔEhf. By contrast, it leads to ‘heating’ of the 71Ga spins, which has only an indirect effect on ΔEhf by changing the 75As lineshape via dipolar coupling between 71Ga and 75As spins. The result of the two-comb experiment is shown in Fig. 4b: a clear increase of Δνhom for 75As is observed. From model fitting we find that 71Ga ‘heating’ leads to a three times broader homogeneous linewidth Δνhom ≍ 355 Hz of 75As and its homogeneous lineshape is modified towards Gaussian, observed as an increase in k ≍ 2.32.
To explain this result we note that the NMR lineshape is a statistical distribution of NMR frequency shifts of each nucleus produced by its dipolar interaction with all possible configurations of the neighbouring nuclear spins. However, in a frequency-comb experiment the evolution of the 75As spin is limited in time by its depolarization. If the nuclear spin environment of each 75As nucleus does not go through all possible configurations during the 75As characteristic depolarization time, the frequency shifts are effectively static, and hence are eliminated from the lineshape, as for any other inhomogeneous broadening.
Thus, we conclude that the narrowed, non-Gaussian (k ≍ 1.6–1.8) homogeneous NMR lineshape arises from the ‘snapshot’ nature of the frequency-comb measurement, probing the strongly frozen nuclear spin configuration. When the additional 71Ga ‘heating’ excitation is applied it ‘thaws’ the 71Ga spins, detected as broadening of the 75As lineshape (as demonstrated in Fig. 4a, b). If all isotopes were fully ‘thawed’ we would have observed a close-to-Gaussian (k ≫ 1) lineshape. By contrast, in the case of completely frozen flip-flops, the lineshape should be close to Lorentzian (k = 1), ultimately limited by the longitudinal nuclear spin relaxation. In a real experiment some spin fluctuations are always present: in particular the spins depolarized by the frequency comb influence one another via homonuclear dipolar interaction, resulting in a homogeneously broadened lineshape with some intermediate k > 1. This interpretation is further supported by a microscopic Bloch equation model of the frequency-comb experiments, as discussed in Supplementary Note 5C.
We use the 75As lineshape as a probe to measure the dynamics of the 71Ga equilibrium spin bath fluctuations. Rather than performing lengthy measurements of the entire 75As lineshape, we excite its spins with a frequency comb with a fixed fMS = 903 Hz, for which the 75As depolarization dynamics is most sensitive to the 71Ga ‘heating’. We find that the resulting 75As depolarization is well described by a stretched exponential function ∝exp[−(trf/τAs)r] with r ≍ 0.6–0.9 (see Methods); the measured value of τAs is used to characterize the response of 75As to 71Ga ‘heating’. Furthermore, we now use selective ‘heating’ of either the −1/2 ↔ +1/2 CT or the + 1/2 ↔ +3/2 ST of 71Ga. The amplitude β1, Ga of the ‘heating’ frequency comb is varied—the resulting dependences of the 75As depolarization time τAs at different 75As comb amplitudes β1, As are shown in Fig. 4c, d for CT and ST ‘heating’, respectively. For analysis we also express β1, Ga in terms of the rf-induced 71Ga spin-flip time τGa ∝ β1, Ga−2 (top scales in Fig. 4c, d, see details in Methods).
For vanishing 71Ga excitation (β1, Ga < 2 nT Hz−1/2, τGa > 20 s) the rf-induced spin-flip time τGa of 71Ga is much larger than the correlation time τc of the 71Ga intrinsic spin flip-flops (τGa > τc). By contrast, strong ‘heating’ (β1, Ga > 200 nT Hz−1/2, τGa < 2 ms) completely ‘thaws’ the 71Ga spins (τGa < τc), broadens the 75As lineshape (via heteronuclear interaction), and is observed as a reduction of τAs. Another clear trend in Fig. 4c, d is that the τAs(β1, Ga) dependence becomes less pronounced at small β1, As. This is because 75As nuclei probe 71Ga spin fluctuations on a timescale of the 75As spin depolarization ∝β1, As−2. At very small β1, As the 75As spin evolution time becomes longer than τc, hence the 75As lineshape is broadened by intrinsic 71Ga fluctuations, and additional 71Ga heating leads only to a minor reduction in τAs. As we now show, this effect allows τc to be deduced from the measurements with variable β1, As and β1, Ga shown in Fig. 4c, d.
First, as we show in Supplementary Note 5B, the heating-induced spin flips (with correlation time τGa) and intrinsic dipolar flip-flops (with correlation time τc) of 71Ga have the same effect on 75As. Therefore, τAs depends only on the effective correlation time (τGa−1 + τc−1)−1 of 71Ga fluctuations. Second, as discussed above, 75As homogeneous broadening is determined by fluctuations of 71Ga only during the characteristic 75As depolarization time. Consequently, the 75As homogeneous linewidth, and hence τAs, depend only on the ratio of the 71Ga effective correlation time and the 75As characteristic evolution time (∝β1, As−2). This ratio is proportional to β1, As2(τGa−1 + τc−1)−1 and τAs is its function. Although the analytical expression for this function is not known, it can be written as a Taylor series, from which we find that τAs depends linearly on (τGa−1 + τc−1)−1 in the limit of small β1, As (see details in Supplementary Note 4). Taking into account that (τGa−1 + τc−1)−1 ∈ (0, τc) and (τGa−1 + τc−1)−1 = τc/2 when τc = τGa, we find that τc can be estimated as the value of τGa for which τAs is a mean of its minimum and maximum values. From the measurements with the smallest β1, As = 3.4 nT Hz−1/2 we estimate in a straightforward way τc, CT ∼ 0.5 s and τc, ST ∼ 1.5 s for CT and ST respectively. A more accurate derivation of τc is achieved by fitting the entire τAs data set with a stretched exponential function of β1, As2(τGa−1 + τc−1)−1, as shown by the lines in Fig. 4c, d (see details in Methods and Supplementary Note 4). Fitting yields correlation times τc, CT ≍ 1.0 ± 0.2 s for CT and τc, ST ≍ 6.2 ± 2.5 s for ST. Furthermore, in Supplementary Note 5 we reproduce the experimental data of Fig. 4c and d with a numerical model based on Bloch equations. We then successfully verify the fitting procedure used here to derive τc by applying it to numerical model results with known τc.
The observed τc ≳ 1 s greatly exceeds typical nuclear dipolar flip-flop times in strain-free III–V solids τc ∼ 100 μs (refs 9,10,17). We attribute the extremely long τc in self-assembled quantum dots to the effect of inhomogeneous nuclear quadrupolar shifts making nuclear spin flip-flops energetically forbidden20,24. This interpretation is corroborated by the observation of τc, ST > τc, CT, because quadrupolar broadening of the ST transitions is much greater than that of the CT transitions (ref. 21). Furthermore, the 71Ga spins examined here have the largest gyromagnetic ratio γ and the smallest quadrupolar moment Q, so we expect that all other isotopes in InGaAs have even longer τc, resulting in the overall τc ≳ 1 s of the entire quantum dot nuclear spin bath. This implies that in high magnetic fields the spin-echo coherence times of the electron and hole spin qubits in self-assembled dots are not limited by the nuclear spin bath up to sub-second regimes9,10,12,28,29. Therefore, the effort aimed at achieving III–V semiconductor quantum dot spin qubits with long coherence should be focused on understanding other mechanisms of central spin dephasing, such as electron-mediated nuclear–nuclear interactions, nuclear spin dynamics induced by electron spin manipulation, or charge fluctuations13,14,15.
Because the frequency-comb technique is not limited by artefacts in the spin dynamics hampering pulsed magnetic resonance, it allows detection of very slow spin bath fluctuations. Such sensitivity of the method can be used, for example, to investigate directly the effect of the electron or hole on the spin bath fluctuations in charged quantum dots—arising, for example, from hyperfine-mediated nuclear spin interactions. The experiments are well understood within a classical rate equation model and confirmed by a microscopic Bloch equation model, although further advances in frequency-comb spectroscopy can be expected with the development of a full quantum mechanical model. Furthermore, the simple and powerful ideas of frequency-comb NMR spectroscopy can be readily extended beyond quantum dots: as we show in Supplementary Note 3, the only essential requirement is that the longitudinal relaxation time T1 should be larger (by about two orders of magnitude) than the transverse relaxation time T2, which is usually the case in solid state spin systems. Finally, our approaches in the use of frequency combs can go beyond NMR, enriching, for example, the techniques in optical spectroscopy.
Methods
Sample structures and experimental techniques.
The experiments were performed on individual neutral self-assembled InGaAs/GaAs quantum dots. The sample was mounted in a helium-bath cryostat (T = 4.2 K) with a magnetic field Bz = 8 T applied in the Faraday configuration (along the sample growth and light propagation direction Oz). A radiofrequency (rf) magnetic field Brf perpendicular to Bz was induced by a miniature copper coil. Optical excitation was used to induce nuclear spin magnetization exceeding 50%, as well as to probe it by measuring hyperfine shifts in photoluminescence spectroscopy21.
Two sample structures have been studied, both containing a single layer of InGaAs/GaAs quantum dots embedded in a weak planar microcavity with a Q-factor of ∼250. In one of the samples the dots emitting at ∼945 nm were placed in a p–i–n structure, where application of a large reverse bias during the rf excitation ensured the neutral state of the dots. The results for this sample are shown in Fig. 2. The second sample was a gate-free structure, where most of the dots emitting at ∼914 nm are found in a neutral state, although the charging can not be controlled. Excellent agreement between the lineshapes of both 71Ga and 75As in the two structures was found, confirming the reproducibility of the frequency-comb technique. The results for this second sample are shown in Fig. 4.
Rate equation model for homogeneous lineshape derivation.
Let us consider an ensemble of spin I = 1/2 nuclei with gyromagnetic ratio γ and inhomogeneously broadened distribution of nuclear resonant frequencies νnuc. We assume that each nucleus has a homogeneous absorption lineshape L(ν), with normalization ∫ −∞+∞L(ν)dν = 1. A small amplitude (non-saturating) rf field will result in depolarization, which can be described by a differential equation for population probabilities p±1/2 of the nuclear spin levels Iz = ±1/2

For frequency-comb excitation the decay rate is the sum of the decay rates caused by each rf mode with magnetic field amplitude B1, and can be written as:

where the summation goes over all modes with frequencies νj = ν1 + jfMS (ν1 is the frequency of the first spectral mode).
The change in the Overhauser shift Ehf produced by each nucleus is proportional to p+1/2 −p−1/2 and, according to equation (2) has an exponential time dependence ∝exp(−W(νnuc)t). The quantum dot contains a large number of nuclear spins with randomly distributed absorption frequencies. Therefore, to obtain the dynamics of the total Overhauser shift we need to average over νnuc. Because the spectrum of the rf excitation is periodic and Δνinh ≫ fMS, the averaging can be done over one period fMS. Furthermore, because the total width of the rf frequency comb Δνcomb is much larger than fMS and Δνhom, the summation in equation (3) can be extended to ±∞. Thus, the following expression is obtained for the time dependence ΔEhf(t, fMS), describing the dynamics of the rf-induced nuclear spin depolarization:

Equation (4) describes the dependence ΔEhf(t, fMS) directly measurable in experiments such as shown in Fig. 2b. ΔEhf(t → ∞) is the total optically induced Overhauser shift of the studied isotope and is also measurable, whereas fMS and B1 are parameters that are controlled in the experiment. We note that in the limit of small mode spacing, fMS → 0, the infinite sum in equation (4) tends to the integral ∫−∞+∞L(ν)dν = 1 and the Overhauser shift decay is exponential (as observed experimentally) with a characteristic time

Equation (4) is a Fredholm integral equation of the first kind on the homogeneous lineshape function L(ν). This is an ill-conditioned problem: as a result finding the lineshape requires some constraints to be placed on L(ν). Our approach is to use the model lineshape of equation (1). After substituting L(ν) from equation (1), the right-hand side of equation (4) becomes a function of the parameters Δνhom and k, which we then find by least-squares fitting of equation (4) to the experimental dependence ΔEhf(t, fMS).
This model is readily extended to the case of I > 1/2 nuclei. Equation (2) becomes a tri-diagonal system of differential equations, and the solution (equation (3)) contains a sum of multiple exponents under the integral. These modifications are straightforward but tedious, and can be found in Supplementary Note 2.
Derivation of the nuclear spin bath correlation times.
Accurate lineshape modelling is crucial in revealing the 75As homogeneous broadening arising from 71Ga ‘heating’ excitation (as demonstrated in Fig. 4a, b). However, because a measurement of the full ΔEhf(t, fMS) dependence is time consuming, the experiments with variable comb amplitudes β1, Ga and β1, As (Fig. 4c, d) were conducted at a fixed fMS = 903 Hz well in excess of the 75As homogeneous linewidth Δνhom ≍ 117 Hz. To extract the 75As depolarization time τAs we fit the 75As depolarization dynamics ΔEhf(t) with the following formula: ΔEhf(trf) = ΔEhf(trf → ∞) × (1 − exp[−(trf/τAs)r]), using r as a common fitting parameter and τAs independent for measurements with different τGa. We find r ≍ 0.6–0.9, depending on β1, As, and the dependence of τAs on β1, Ga obtained from the fit is shown in Fig. 4c, d by the symbols with error bars corresponding to 95% confidence intervals.
The spacing of the 71Ga ‘heating’ frequency comb is kept at a small value, fMS = 150 Hz, ensuring uniform excitation of all nuclear spin transitions. The amplitude of the ‘heating’ comb is defined as  , where B1 is magnetic field amplitude of each mode in the comb (further details can be found in Supplementary Note 1). To determine the correlation times we express β1, Ga in terms of the rf-induced spin-flip time τGa. The τGa is defined as the exponential time of the 71Ga depolarization induced by the ‘heating’ comb, and is derived from an additional calibration measurement. The values of β1, Ga shown in Fig. 4c are calculated using equation (5) as
, where B1 is magnetic field amplitude of each mode in the comb (further details can be found in Supplementary Note 1). To determine the correlation times we express β1, Ga in terms of the rf-induced spin-flip time τGa. The τGa is defined as the exponential time of the 71Ga depolarization induced by the ‘heating’ comb, and is derived from an additional calibration measurement. The values of β1, Ga shown in Fig. 4c are calculated using equation (5) as  , where γGa is the 71Ga gyromagnetic ratio and τGa is experimentally measured. The additional factor of 4 in the denominator is due to the matrix element of the CT of spin I = 3/2. For experiments on ST the β1, Ga values shown in Fig. 4d are obtained with the same formulae, but multiplied by
, where γGa is the 71Ga gyromagnetic ratio and τGa is experimentally measured. The additional factor of 4 in the denominator is due to the matrix element of the CT of spin I = 3/2. For experiments on ST the β1, Ga values shown in Fig. 4d are obtained with the same formulae, but multiplied by  .
.
The effect of 71Ga heating on 75As (probed with τAs) is controlled by the ratio of the 71Ga effective correlation time (τGa−1 + τc−1)−1 and the characteristic time of 75As rf-induced depolarization 2/(γAs2β1, As2) given by equation (5). The experimental data of Fig. 4c, d are fitted with the function τAs = τAs, min(ΔτAs + (1 − ΔτAs)exp[−(γAs2β1, As2(τGa−1 + τc−1)−1/(2θ))s]), where θ ≍ 0.4, s ≍ 0.6 are dimensionless parameters describing the modified (stretched) exponential function, ΔτAs ≍ 2 is the ratio of τAs without and with strong 71Ga heating, τAs, min is τAs in the limit of large β1, Ga, dependent on β1, As, and τc is the correlation time of the 71Ga spin fluctuations. Further details of the analysis used to derive τc from experimental data can be found in Supplementary Note 4. Moreover, we have verified this fitting procedure by applying it to numerically simulated spin dynamics with known τc, as described in Supplementary Note 5D.
References
Borri, P. et al. Ultralong dephasing time in InGaAs quantum dots. Phys. Rev. Lett. 87, 157401 (2001).
Volker, S. Hole-burning spectroscopy. Annu. Rev. Phys. Chem. 40, 499–530 (1989).
Yang, L. et al. Two-colour spin noise spectroscopy and fluctuation correlations reveal homogeneous linewidths within quantum-dot ensembles. Nature Commun. 5, 5949 (2014).
Hahn, E. L. Spin echoes. Phys. Rev. 80, 580–594 (1950).
Biercuk, M. J. et al. Optimized dynamical decoupling in a model quantum memory. Nature 458, 996–1000 (2009).
Bar-Gill, N. et al. Suppression of spin-bath dynamics for improved coherence of multi-spin-qubit systems. Nature Commun. 3, 858 (2012).
Tyryshkin, A. M. et al. Electron spin coherence exceeding seconds in high-purity silicon. Nature Mater. 11, 143–147 (2012).
Li, D., Dementyev, A. E., Dong, Y., Ramos, R. G. & Barrett, S. E. Generating unexpected spin echoes in dipolar solids with π pulses. Phys. Rev. Lett. 98, 190401 (2007).
Merkulov, I. A., Efros, A. L. & Rosen, M. Electron spin relaxation by nuclei in semiconductor quantum dots. Phys. Rev. B 65, 205309 (2002).
de Sousa, R. & Das Sarma, S. Theory of nuclear-induced spectral diffusion: spin decoherence of phosphorus donors in Si and GaAs quantum dots. Phys. Rev. B 68, 115322 (2003).
Yao, W., Liu, R.-B. & Sham, L. J. Theory of electron spin decoherence by interacting nuclear spins in a quantum dot. Phys. Rev. B 74, 195301 (2006).
Bluhm, H. et al. Dephasing time of GaAs electron-spin qubits coupled to a nuclear bath exceeding 200 μs. Nature Phys. 7, 109–113 (2011).
Press, D. et al. Ultrafast optical spin echo in a single quantum dot. Nature Photon. 4, 367–370 (2010).
De Greve, K. et al. Ultrafast coherent control and suppressed nuclear feedback of a single quantum dot hole qubit. Nature Phys. 7, 872–878 (2011).
Greilich, A., Carter, S. G., Kim, D., Bracker, A. S. & Gammon, D. Optical control of one and two hole spins in interacting quantum dots. Nature Photon. 5, 702–708 (2011).
Hansom, J. et al. Environment-assisted quantum control of a solid-state spin via coherent dark states. Nature Phys. 10, 1745–2473 (2014).
Urbaszek, B. et al. Nuclear spin physics in quantum dots: an optical investigation. Rev. Mod. Phys. 85, 79–133 (2013).
Cai, J., Retzker, A., Jelezko, F. & Plenio, M. B. A large-scale quantum simulator on a diamond surface at room temperature. Nature Phys. 9, 168–173 (2013).
de Sousa, R. & Das Sarma, S. Electron spin coherence in semiconductors: considerations for a spin-based solid-state quantum computer architecture. Phys. Rev. B 67, 033301 (2003).
Chekhovich, E. A., Hopkinson, M., Skolnick, M. S. & Tartakovskii, A. I. Suppression of nuclear spin bath fluctuations in self-assembled quantum dots induced by inhomogeneous strain. Nature Commun. 6, 6348 (2015).
Chekhovich, E. A. et al. Structural analysis of strained quantum dots using nuclear magnetic resonance. Nature Nanotech. 7, 646–650 (2012).
Munsch, M. et al. Manipulation of the nuclear spin ensemble in a quantum dot with chirped magnetic resonance pulses. Nature Nanotech. 9, 671–675 (2014).
Udem, T., Holzwarth, R. & Hansch, T. W. Optical frequency metrology. Nature 416, 233–237 (2002).
Dzhioev, R. I. & Korenev, V. L. Stabilization of the electron-nuclear spin orientation in quantum dots by the nuclear quadrupole interaction. Phys. Rev. Lett. 99, 037401 (2007).
Latta, C., Srivastava, A. & Imamoglu, A. Hyperfine interaction-dominated dynamics of nuclear spins in self-assembled InGaAs quantum dots. Phys. Rev. Lett. 107, 167401 (2011).
Madhu, P. & Kumar, A. Direct cartesian-space solutions of generalized Bloch equations in the rotating frame. J. Magn. Reson. Ser. A 114, 201–211 (1995).
Van Vleck, J. H. The dipolar broadening of magnetic resonance lines in crystals. Phys. Rev. 74, 1168–1183 (1948).
Khaetskii, A. V., Loss, D. & Glazman, L. Electron spin decoherence in quantum dots due to interaction with nuclei. Phys. Rev. Lett. 88, 186802 (2002).
Bechtold, A. et al. Three-stage decoherence dynamics of an electron spin qubit in an optically active quantum dot. Nature Phys 11, 1005–1008 (2015).
Acknowledgements
The authors are grateful to K. V. Kavokin for useful discussions. This work has been supported by the EPSRC Programme Grant EP/J007544/1, ITN S3NANO. E.A.C. was supported by a University of Sheffield Vice-Chancellor’s Fellowship and a Royal Society University Research Fellowship. I.F. and D.A.R. were supported by EPSRC. Computational resources were provided in part by the University of Sheffield HPC cluster ‘Iceberg’.
Author information
Authors and Affiliations
Contributions
M.H., I.F., D.A.R., J.N., R.M.S., A.J.B. and A.J.S. developed and grew the samples. A.M.W. and E.A.C. conceived and designed the experiments and analysed the data. A.M.W. performed the experiments. E.A.C. performed the numerical modelling. E.A.C., A.M.W., M.S.S., A.I.T., G.B. and A.J.B. wrote the manuscript with input from all authors. E.A.C. coordinated the project.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary information
Supplementary information (PDF 10477 kb)
Rights and permissions
About this article
Cite this article
Waeber, A., Hopkinson, M., Farrer, I. et al. Few-second-long correlation times in a quantum dot nuclear spin bath probed by frequency-comb nuclear magnetic resonance spectroscopy. Nature Phys 12, 688–693 (2016). https://doi.org/10.1038/nphys3686
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys3686
This article is cited by
-
Pulse control protocols for preserving coherence in dipolar-coupled nuclear spin baths
Nature Communications (2019)
-
Nuclear spins get a comb-over
Nature Physics (2016)
-
Quantum dot spin coherence governed by a strained nuclear environment
Nature Communications (2016)