Abstract
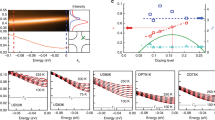
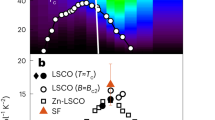
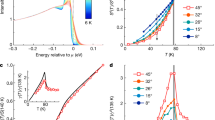
The superconducting temperature Tc of hole-doped high-temperature superconductors has a dome-like shape as a function of hole concentration, with a maximum Tc at ‘optimal’ doping. On the underdoped side, the superconducting state is often described in terms of one energy scale, associated with the maximum of the d-wave gap (at the antinodes), which increases as the doping decreases. Here, we report electronic Raman scattering experiments that show a second energy scale in the gap function: the slope of the gap at the nodes, which decreases with decreasing doping. Our measurements also reveal two distinct quasiparticle dynamics; electronic coherence persists down to low doping levels at the nodes, whereas antinodal quasiparticles become incoherent. Using a sum-rule, we find that the low-frequency Raman response and the temperature dependence of the superfluid density, both controlled by nodal excitations, behave in a qualitatively similar manner with doping variation.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout





Similar content being viewed by others
References
Timusk, T. & Statt, B. W. The pseudogap in high-temperature superconductors: an experimental survey. Rep. Prog. Phys. 62, 61–122 (1999).
Devereaux, T. P. & Einzel, D. Electronic Raman scattering in superconductors as a probe of anisotropic electron pairing. Phys. Rev. B 51, 16336–16357 (1995).
Venturini, F. et al. Doping dependence of the electronic Raman spectra in cuprates. J. Phys. Chem. Solids 63, 2345–2349 (2002).
Sugai, S., Suzuki, H., Takayanagi, Y., Hosokawa, T. & Hayamizu, N. Carrier-density-dependent momentum shift of the coherent peak and the LO phonon mode in p-type high-T c superconductors. Phys. Rev. B 68, 184504 (2003).
Chen, X. K. et al. Electronic Raman scattering in underdoped YBa2Cu3O6.5 . Phys. Rev. B 56, R513–R516 (1997).
Presland, M. R., Tallon, J. L., Buckley, R. G., Liu, R. S. & Flower, N. E. General trends in oxygen stoichiometry effects on T c in Bi and Tl superconductors. Physica C 176, 95–105 (1991).
Chubukov, A. V., Devereaux, T. P. & Klein, M. V. Resonance mode in B1g Raman scattering: A way to distinguish between spin-fluctuation and phonon-mediated d-wave superconductivity. Phys. Rev. B 73, 094512 (2006).
Klein, M. V. & Dierker, S. B. Theory of Raman scattering in superconductors. Phys. Rev. B 29, 4976–4991 (1984).
Hewitt, K. C. & Irwin, J. C. Doping dependence of the superconducting gap in Bi2Sr2CaCu2O8−δ . Phys. Rev. B 66, 054516 (2002).
Bonn, D. A. et al. Surface impedance studies of YBCO. Czech. J. Phys. 46, 3195–3202 (1996).
Panagopoulos, C. & Xiang, T. Relationship between the superconducting energy gap and the critical temperature in high-T c superconductors. Phys. Rev. Lett. 81, 2336–2339 (1998).
Lee, P. A. & Wen, X. G. Unusual superconducting state of underdoped cuprates. Phys. Rev. Lett. 78, 4111–4114 (1997).
Wen, X. G. & Lee, P. A. Theory of quasiparticles in the underdoped high-T c superconducting state. Phys. Rev. Lett. 80, 2193–2196 (1998).
Ioffe, L. B. & Millis, A. J. d-wave superconductivity in doped Mott insulators. J. Phys. Chem. Solids 63, 2259–2268 (2002).
Broun, D. M. et al. Superfluid density reveals a quantum critical point between d-wave superconductivity and a Mott insulator. Preprint at <http://arxiv.org/cond-mat0509223> (2005).
Anderson, P. W. The resonating valence bond state in La2CuO4 and superconductivity. Science 235, 1196–1198 (1987).
Kotliar, G. & Liu, J. The superexchange mechanism and d-wave superconductivity. Phys. Rev. B 38, 5142–5145 (1988).
Gros, C. Superconductivity in correlated wave functions. Phys. Rev. B 38, 931–934 (1988).
Anderson, P. W. et al. The physics behind high-temperature superconducting cuprates: the plain vanilla version of RVB. J. Phys. Condens. Matter 16, R755–R769 (2004).
Yoshida, T. et al. Metallic behavior of lightly doped La2−xSrxCuO4 with a Fermi surface forming an arc. Phys. Rev. Lett. 91, 027001 (2003).
Shen, K. M. et al. Nodal quasiparticles and antinodal charge ordering in Ca2−xNaxCuO2Cl2 . Science 307, 901–904 (2005).
Mesot, J. et al. Superconducting gap anisotropy and quasiparticle interaction: A doping dependent photoemission study. Phys. Rev. Lett. 83, 840–843 (1999).
Borisenko, S. V. et al. Superconducting gap in the presence of bilayer splitting in underdoped (Pb,Bi)2Sr2CaCu2O8−δ . Phys. Rev. B 66, 140509(R) (2002).
Norman, M. R. et al. Destruction of the Fermi surface in underdoped high-T c superconductors. Nature 392, 157–160 (1998).
Benfatto, L., Caprara, S. & Di Castro, C. Gap and pseudogap evolution within the charge-ordering scenario for superconducting cuprates. Eur. Phys. J. B 17, 95–102 (2000).
Chakravarty, S., Laughlin, R. B., Morr, D. K. & Nayak, C. Hidden order in the cuprates. Phys. Rev. B 63, 094503 (2001).
Won, H., Haas, S., Parker, D. & Maki, K. High-Tc cuprate superconductivity in a nutshell. Phys. Status Solidi B 242, 363–369 (2005).
Campuzano, J. C. et al. Electronic spectra and their relation to the (π,π) collective mode in high-T c superconductors. Phys. Rev. Lett. 83, 3709–3712 (1999).
Ding, H. et al. Coherent quasiparticle weight and its connection to high-T c superconductivity from angle-resolved photoemission. Phys. Rev. Lett. 87, 227001 (2001).
Sutherland, M. et al. Thermal conductivity across the phase diagram of cuprates: Low-energy quasiparticles and doping dependence of the superconducting gap. Phys. Rev. B 67, 174520 (2003).
McElroy, K. et al. Coincidence of checkerboard charge order and antinodal state decoherence in strongly underdoped superconducting Bi2Sr2CaCu2O8+δ . Phys. Rev. Lett. 94, 197005 (2005).
Miyakawa, N., Guptasarma, P., Zasadzinski, J. F., Hinks, D. G. & Gray, K. E. Strong dependence of the superconducting gap on oxygen doping from tunneling measurements on Bi2Sr2CaCu2O8−δ . Phys. Rev. Lett. 80, 157–160 (1998).
Miyakawa, N. et al. Predominantly superconducting origin of large energy gaps in underdoped Bi2Sr2CaCu2O8−δ from tunneling spectroscopy. Phys. Rev. Lett. 83, 1018–1021 (1999).
DeWilde, Y. et al. Unusual strong-coupling effects in the tunneling spectroscopy of optimally doped and overdoped Bi2Sr2CaCu2O8−δ . Phys. Rev. Lett. 80, 153–156 (1998).
Hoffman, J. E. et al. Imaging quasiparticle interference in Bi2Sr2CaCu2O8+δ . Science 297, 1148–1151 (2002).
Deutscher, G. Coherence and single-particle excitations in the high-temperature superconductors. Nature 397, 410–412 (1999).
Stojkovic, B. P. & Pines, D. Theory of the longitudinal and Hall conductivities of the cuprate superconductors. Phys. Rev. B 55, 8576–8595 (1997).
Ioffe, L. B. & Millis, A. J. Zone-diagonal-dominated transport in high-T c cuprates. Phys. Rev. B 58, 11631–11637 (1998).
Honerkamp, C., Salmhofer, M., Furukawa, N. & Rice, T. M. Breakdown of the Landau–Fermi liquid in two dimensions due to umklapp scattering. Phys. Rev. B 63, 035109 (2001).
Katanin, A. A. & Kampf, A. P. Quasiparticle anisotropy and pseudogap formation from the weak-coupling renormalization group point of view. Phys. Rev. Lett. 93, 106406 (2004).
Civelli, M., Capone, M., Kancharla, S. S., Parcollet, O. & Kotliar, G. Dynamical breakup of the Fermi surface in a doped mott insulator. Phys. Rev. Lett. 95, 106402 (2005).
Sénéchal, D. & Tremblay, A. M. S. Hot spots and pseudogaps for hole- and electron-doped high-temperature superconductors. Phys. Rev. Lett. 92, 126401 (2004).
Bertinotti, A. et al. in Studies of High Temperature Superconductors Vol. 23 (ed. Narlikar, A.) 27–85 (Nova Science Publishers, New York, 1997).
Le Tacon, M., Sacuto, A. & Colson, D. Two distinct electronic contributions in the fully symmetric Raman response of high T c cuprates. Phys. Rev. B 71, 100504(R) (2005).
Opel, M. et al. Carrier relaxation, pseudogap, and superconducting gap in high-T c cuprates: A Raman scattering study. Phys. Rev. B 61, 9752–9844 (2000).
Larkin, A. I. Effect of collective excitations on the electrodynamics of superconductors. Sov. Phys. JETP 19, 1478–1486 (1964).
Leggett, A. J. Theory of a superfluid Fermi liquid. I. General formalism and static properties. Phys. Rev. 140, A1869–A1888 (1965).
Freericks, J. K., Devereaux, T. P., Moraghebi, M. & Cooper, S. L. Optical sum rules that relate to the potential energy of strongly correlated systems. Phys. Rev. Lett. 94, 216401 (2005).
Shastry, S. & Shraiman, B. Theory of Raman scattering in Mott-Hubbard systems. Phys. Rev. Lett. 65, 1068–1071 (1990).
Acknowledgements
We are grateful to S. Biermann, N. Bontemps, S.V. Borisenko, P. Bourges, M. Cazayous, R. Combescot, L. ’de Medici, T.P. Devereaux, K. McElroy, P. Monod, M. Norman, Z.-X. Shen, and L. Taillefer for useful discussions. This research was supported by CNRS, Ecole Polytechnique and the ‘Chaire Blaise Pascal de la Fondation de l’Ecole Normale Supérieure et de la région Ile de France’.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
About this article
Cite this article
Le Tacon, M., Sacuto, A., Georges, A. et al. Two energy scales and two distinct quasiparticle dynamics in the superconducting state of underdoped cuprates. Nature Phys 2, 537–543 (2006). https://doi.org/10.1038/nphys362
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys362
This article is cited by
-
An electronic nematic liquid in BaNi2As2
Nature Communications (2022)
-
Strange semimetal dynamics in SrIrO3
Nature Communications (2020)
-
Fractionalizing a Local Pair Density Wave: a Good “Recipe” for Opening a Pseudo-gap
Journal of Superconductivity and Novel Magnetism (2020)
-
Putting the gap on the map
Nature Physics (2019)
-
Intimate link between charge density wave, pseudogap and superconducting energy scales in cuprates
Nature Physics (2019)