Main

Here we sought to separate the mechanical component of intercellular communication from indirect effects, such as a change in the amount or type of secreted chemo-attractants. We did so by introducing a ‘mechanical cell’. The ‘mechanical cell’ consists of a probe that mimics the mechanical aspect of a cell by generating substrate deformations identical to the ones induced by a neighbouring beating cell. Previous studies have shown that mechanical stimulation of a quiescent cell or an engineered cardiac construct can induce beating12,14. However, in those studies, the magnitude and direction of forces applied were not controlled as to mimic the magnitude and direction of forces applied by cells. In addition, the duration of stimulation was extremely brief and the cells did not synchronize with the probe. These studies therefore did not provide a demonstration or characterization of cellular mechanical communication.

Here, we use a ‘mechanical cell’ to apply deformations identical to those generated by an aligned beating cardiac cell both in magnitude and in directionality. We show that such deformations can synchronize cell beating. This provides clear evidence for mechanical cellular communication. Training of both quiescent and spontaneously beating cells takes up to 10–15 min and the induced beating frequency persists for over an hour after stimulation had stopped. These results demonstrate that mechanical communication is a unique type of interaction that is both long ranged and induces long-lasting alterations in interacting cells. We further demonstrate that mechanical communication reduces the electromechanical delay variability between cells and thereby provides a mechanism to ensure that the same amount of time is required for different cells to convert action potential evoked by electrical stimulation to physical contraction.

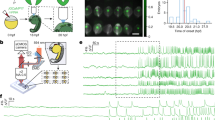
Primary neonatal rat cardiomyocytes were cultured on laminin-coated polyacrylamide (PA) gels with elastic modulus of 3.8 ± 0.2 kPa as measured by atomic force microscopy. Substrate stiffness in this range was shown to support optimal spontaneous cardiac cell beating7. Tissue stiffness increases during cardiac development, and substrates slightly softer than adult heart elasticity are required to support optimal beating of neonatal cardiomyocytes in culture15,16. Surprisingly, aligned beating cells which reside at a distance that allows their deformation fields to overlap, synchronize their spontaneous beating frequency (see Fig. 1a and Supplementary Fig. 13 and Supplementary Movies 1 and 5). As the cells do not have any physical contact, no gap junctions are present. It seems likely that these cells sense each other mechanically through the deformation field they induce in the substrate. To test this hypothesis, we designed a device that allows us to mimic the mechanical deformations generated by a beating cardiac cell on its neighbours (Fig. 1e). Using this device we can explore the mechanical component of the interaction. The device is composed of a tungsten probe mounted on a piezo stage with X–Y –Z actuators. Driven by the actuators, the probe cyclically pulls the substrate towards and away from the cardiac cell at varying frequencies. As there is no physical contact between the cell and the probe, the interaction is mediated solely by mechanical deformations in the substrate.

Figure 1: Mimicking neighbouring beating cardiac cell deformations using a mechanical probe.
figure 1

a, The normalized calcium signal (right) and phase map (left) of a synchronized pair of beating cardiac cells 50 μm apart on a 3.8 kPa substrate. b, Deformation field generated by the left beating cardiac cell in a (Supplementary Movie 1). The red ellipse represents the position of a neighbouring cardiac cell. The Y -axis represents the direction of contraction. Given that cardiac cells contract along the average direction of sarcomere filaments alignment (Supplementary Movie 4), the Y -axis represents also the director of sarcomere alignment. Lattice spacing is 2 μm. c, Average amplitude of deformations generated in the vicinity of a cardiac cell as a result of a neighbouring beating cell (solid, black) or as a result of probe oscillations (dashed, red), see Supplementary Section 2 for additional details. d, The deformation field in the vicinity of a cardiac cell generated by a neighbouring beating cell (right) or by the probe (left). Notice that probe oscillations must be perpendicular to the Y axis to mimic correctly cell-induced deformations. e, Schematic representation of the experimental set-up. A tungsten probe applies an oscillatory stretch, thereby deforming the underlying substrate.

Full size image

By incorporating 0.2 μm fluorescent beads in the PA substrate and tracking them over time, we quantified the deformation field generated by two synchronized beating cardiac cells with no physical contact (Fig. 1b and Supplementary Movie 1). The amplitude and direction of the mechanical deformations generated by the probe were chosen such as to mimic the deformations sensed by a cell in this case (Fig. 1c, d and Supplementary Section 2). Hence, the probe is essentially a ‘mechanical cell’.

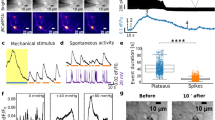
Cardiac cells were loaded with the fluorescent indicator Fluo-4 and calcium oscillations were monitored using spinning disc confocal microscopy. The beating rate of each cell was recorded before probe activation and after ten minutes of mechanical stimulation when the cell reaches a stationary behaviour. Henceforth, we will denote by ω0 the spontaneous beating frequency of the cell before probe activation and by ωcell its beating rate after it reaches stationary behaviour with probe oscillations. Figure 2a shows the dependence of cell beating frequency, ωcell, on the frequency of applied mechanical deformations by the probe, ωprobe, normalized by ω0. As clearly observed, an isolated cardiac cell can be trained to beat at a given frequency by deforming locally the underlying substrate with a mechanical probe. The probe can induce regular beating in a quiescent cell (Fig. 2e) or in a cell with irregular beating (Fig. 2d) and reprogram the cell beating frequency (Fig. 2a–c and Supplementary Movie 2). In all cases, after a ‘training period’, the cell synchronizes its beating frequency with that of the mechanical probe.

Figure 2: ‘Reprogramming’ of cardiac cell beating by a mechanical probe.
figure 2

a, Cell beating frequency after ten minutes of mechanical stimulation (ωcell) as a function of probe frequency (ωprobe) normalized by the spontaneous beating frequency of the cell before probe activation (ω0). Each point represents a single cell experiment (n = 30). Notice that above ωprobe/ω0 = 2.5, cell dynamics turn into ‘bursting’ behaviour with two timescales (blue circles); a fast frequency that equals ωprobe and a slow frequency that equals ω0. The left and right insets at the top of the figure represent the normalized calcium signal for the linear behaviour and the ‘bursting behaviour’, respectively. b, Representative bursting behaviour of a cell stimulated with a frequency ωprobe/ω0 > 2.5: wavelet (top) and normalized calcium signal (bottom). Corresponds to Supplementary Movie 3. c, Normalized calcium signal (F/F0) for a cell that was reprogrammed into beating at 0.5 Hz (using a 0.5 Hz oscillating probe, top) and at 1 Hz (using a 1 Hz oscillating probe, bottom). Corresponds to Supplementary Movie 2. d, An irregularly beating cardiac cell (top) is induced to beat regularly at a frequency dictated by a mechanical probe (bottom). e, A quiescent cell (top) is paced (bottom) using a mechanical probe.

Full size image

Monitoring mechanical deformations next to the cell edge after it had synchronized with the probe reveals that the cell and the probe beat most of the time in phase (Supplementary Fig. 3) with transient anti-phase beating behaviour (Supplementary Fig. 5). In addition, we found that the deformations generated by the probe next to the cell edge equal those generated by the beating cell itself along that axis (Supplementary Section 2 and Supplementary Fig. 5). This was found to be the case also in pairs of synchronized beating cardiac cells (Supplementary Fig. 6).

Cells can follow the probe oscillation frequency up to a threshold of ωprobe/ω0 = 2.5. At higher probe oscillation frequencies, cell dynamics turn into a bursting behaviour involving fast and slow timescales (Fig. 2a, b and Supplementary Movie 3). The fast frequency is dictated by the probe, whereas the slow frequency equals ω0. In our system bursting behaviour is not observed with electrical field stimulation in the range of frequencies screened (up to ωprobe/ω0 ∼ 10, see Fig. 3).

Figure 3: Mechanical stimulation induces long-term changes in the cell whereas electrical field stimulation is transient.
figure 3

a, Cell beating frequency, ωcell, normalized by ω0 (right) and by the stimulation frequency, ωstim (left) ten minutes after stimulation had stopped for mechanical stimulation (MS, blue) and electrical field stimulation (EFS, red). Each point represents a single cell experiment MS (n = 6), EFS (n = 23). b, Representative behaviour of a cell stimulated with a frequency of 1 Hz by a mechanical probe (empty blue squares) and by EFS (filled red circles). In both cases the spontaneous beating frequency of the cell before stimulation was ω0 = 0.4 Hz. c, Cell beating frequency as a function of stimulation frequency, ωstim, normalized by ω0 for MS (top) and EFS (bottom) after the addition of GsMtx-4, MS (n = 7), EFS (n = 15). d, Same as in c but after the addition of BDM instead of GsMtx-4, MS (n = 9), EFS (n = 23). e, Cells stimulated in the direction parallel to sarcomere alignment did not respond to the mechanical stimulus. Only cells stimulated in the direction perpendicular to sarcomere orientation were paced.

Full size image

Cardiac cell synchronized beating is usually achieved by electrical field stimulation (EFS). Cells stimulated using EFS return to their original beating frequency as soon as the stimulation stops (Fig. 3a, b). In contrast, we found that, surprisingly, the beating rate induced by the mechanical probe was maintained by the cell for over an hour after the stimulation had been ceased. This was true even for induced bursting behaviour (Fig. 3a, b). The long timescale required for training a beating cell and for the relaxation of the induced beating rate after stimulation stops, implies that long-term modifications occur within the cell in response to the forces involved in mechanical communication.

Cardiac cell spontaneous contractions arise from self-sustained oscillations of the intracellular calcium concentration, and can therefore be regarded as a calcium oscillator. A minimal simplified model for the kinetic scheme that underlies calcium oscillations can be formulated as a system of coupled differential equations (for details see Supplementary Section 1). Its solution determines the spontaneous calcium oscillation frequency. The oscillation frequency of this ‘calcium oscillator’ can be paced by a periodic flow of calcium ions into the system above a threshold (Supplementary Fig. 1c) or by changing the value of the kinetic rate constants of the oscillator (Supplementary Fig. 1d).

A periodic flow can model the effect of EFS where plasma membrane depolarization induces an influx of calcium ions into the cytoplasm through voltage-sensitive ion channels. However, if only calcium flow is involved, the induced frequency returns to its original value as soon as the stimulation stops. If mechanical stimulation were to induce a frequency change in an analogous mechanism (only by opening mechanosensitive ion channels instead of voltage-sensitive ones), the induced frequency should have been transient as well. The persistence of the induced beating rate after mechanical stimulation ends suggests that this is not the case. Furthermore, several complementary experiments suggest that stretch-activated ion channels (SAC) are not necessary in our system for mechanical communication (Fig. 3c and Supplementary Sections 3 and 4).

A change in the value of the ‘calcium oscillator’ kinetic rate constants, on the other hand, would persist after stimulation had stopped, and can therefore account for the long-lived change induced by mechanical stimulation (Fig. 3a, b). This would require biochemical alterations in the cell, ones that can be regulated by mechanosensitive elements in the cytoskeleton. Cardiac cell mechanosensing through a non-SAC-related mechanism was recently observed17,18,19. It was shown to involve increased sensitivity of type 2 Ryanodine receptor (RyR2) channels, which are known to regulate cardiac cells’ beating rates20,21 in a process dependent on microtubules and not influenced by stretch-activated channels. Our data suggest that microtubule structural integrity is necessary for mechanical communication (see Supplementary Section 4).

Next, we noticed that the direction of the stimulation is of fundamental importance. Cells stimulated in the direction parallel to sarcomere alignment did not respond to the mechanical stimulus. Only cells stimulated in the direction perpendicular to sarcomere orientation were paced (Fig. 3e). Notice that the direction perpendicular to sarcomere alignment is identical to that of the deformations generated by an adjacent beating cardiac cell (Fig. 1b, d and Supplementary Section 2).

The strong dependence of mechanical stimulation on the direction of probe-induced deformations argues for the involvement of the sarcomeric structure in the mechanosensing process. To further test the role of the contractile machinery in mechanosensing, cardiac cells were treated with 2,3-butanedione monoxime (BDM), a potent inhibitor of actin–myosin interaction. BDM inhibits cardiac cell contraction while maintaining calcium oscillation. Treatment with BDM allows for pacing of the oscillatory calcium signal by EFS (Fig. 3d). In contrast, mechanical pacing of the oscillatory calcium signal by the probe is completely abolished (Fig. 3d). Taken together, the dependence of mechanical stimulation on actin–myosin interaction and on the direction of probe-induced deformations demonstrates that the contractile machinery actively participates in the mechano-sensing process.

Ventricular myocardium is arranged in highly oriented layers that are about two to four cells thick. These layers are embedded into a dense connective three-dimensional tissue network and are interconnected by branches of cardiomyocytes and fibroblasts. Locally, cardiomyocytes have a nearly parallel alignment, which as we have shown here is optimal for mechanical communication. The presence of gap junctions between neighbouring cells ensures proper propagation of the electrical potential and, therefore, a continuous wave of contraction.

The differences observed in this work between mechanical and electrical stimulation, mainly the ability of cells to maintain a mechanically induced frequency for over an hour, may indicate that mechanical communication may have a role in the mature heart different from that of electrical conduction.

Pacemaker cells synchronize action potential generation of cardiac cells to achieve synchronized cardiac cell beating. However, a finite time, termed the electromechanical delay (EMD) is required to convert the electrical signal into a mechanical contraction. The value of the EMD should depend on the dynamics of calcium release and force generation, and is therefore expected to vary among individual cells22. Cell-to-cell EMD variability may in theory cause cells with synchronized action potential to beat with a phase shift. As pacemaker cells do not synchronize physical contraction directly, a mechanism must exist that ensures that synchronized generation of action potential will lead to synchronized contraction.

We would like to suggest that mechanical coupling between cells reduces cell-to-cell EMD variability, therefore ensuring that the final outcome of action potential pacing is synchronized beating.

To test this hypothesis in a set-up that is still two-dimensional but mimics better the connectivity and alignment of cardiomyocytes in the heart, we monitored calcium dynamics in groups of aligned cardiac cells in electrically paced culture. Differences in calcium dynamics between individual cells will translate into EMD variability and unsynchronized contraction. We characterize the difference in calcium dynamics between cells by measuring the peak-to-peak time difference (Fig. 4a) and the calcium transient decay time ratio (Fig. 4b).

Figure 4: Time delay between calcium signals of electrically paced cells.
figure 4

a,b, Peak-to-peak time difference, Δt (a) and calcium transient decay time ratio, τ2/τ1 (b) between calcium signals of cells under electrical field stimulation. Error bars represent s.e.m. As the cells generated action potential at the same time, the difference in calcium dynamics corresponds to biochemical differences between the cells. Notice that the variability in calcium dynamics is much smaller when mechanical communication is not inhibited. c, Representative calcium signals of two cells in physical contact. d, Representative calcium signals of two cells in physical contact treated with BDM for 5 h. ∗∗∗P < 0.001. P-values were determined according to the unpaired one-tailed Mann–Whitney test.

Full size image

Isolated cells that do not interact mechanically but are still paced using EFS have major differences in calcium dynamics (Fig. 4). On the other hand, calcium signals of beating cardiac cells in physical contact are nearly identical (Fig. 4c). Physical contact in this context can be either direct or via neighbouring cells. In the presence of BDM, where mechanical communication is abolished (Fig. 3d), cardiac cells in physical contact develop a delay between their calcium signals similar to that of isolated cells (Fig. 4d). Similar results were obtained with blebbistatin (Supplementary Fig. 8).

These results strongly support the notion that mechanical communication is essential for converting electrical pacing into synchronized beating.

We demonstrate that mechanical communication has an important role in synchronized beating of neonatal cardiomyocytes and have clear indications that adult cells can be paced mechanically in a similar way (see Supplementary Section 5). As mechanical coupling depends on the elastic properties of the environment, disruption of the normal mechanical environment (for example, scar tissue formation following myocardial infraction) can impair this interaction and lead to a discoordinate contraction termed dyssynchrony with a high risk for heart failure23.

Methods

All laboratory procedures conform to the Guide for the Care and Use of Laboratory Animals published by the US National Institutes of Health. Animal usage was approved by the Animal Care and Use Committee of the Technion, Israel Institute of Technology.

Cell culture.

Neonatal cardiomyocytes were isolated from zero-day-old Sprague Dawley (SD) rat pups using the Neonatal Cardiomyocyte Isolation System (Worthington) according to the manufacturer’s instructions. Briefly, hearts were rinsed with ice-cold Hank’s balanced salt solution (HBSS) and trypsinized for 16 h at 4 °C. Following trypsinization, hearts were incubated with trypsin inhibitor at 37 °C, and then with collagenase solution for 30 min. Cells were triturated, pelleted and resuspended in L15 media (Worthington). Cells were then subjected to a Percoll gradient for separation of cardiomyocytes from non-myocytes, as described before24. Isolated cardiomyocytes were resuspended with culture media: F10 media (Sigma-Aldrich) supplemented with 5% fetal calf serum (Biological Industries), 5% donor horse serum (Life Technologies), penicillin 100 units ml−1, streptomycin 0.1 mg ml−1, 5-Bromo-2′-deoxyuridine (5-BrdU) 0.05 mg ml−1 and CaCL2 1 mM (Sigma-Aldrich). Approximately 1 × 105 cells were plated in 30 mm glass-bottom plates (Greiner) covered with laminin-coated PA gel, as described below. Cultured cardiomyocytes were grown for at least 72 h and up to 6 days.

Recording intracellular calcium transients.

Cells were loaded with Ca2+ indicator, fluo-4, acetoxymethylester (fluo-4 AM), (Life Technologies). Following incubation of 5 μM fluo-4AM for 30 min at RT in F10 media, cells were washed and recovered for 10 min in complete growth medium at 37 °C. Intracellular calcium transient was recorded in the presence and absence of either 10 mM 2,3-butanedione monoxime (BDM) (Sigma-Aldrich) or 4 μM GsMtx-4 (Alamone).

Visualization of F-actin in cultured myocytes.

24 h following plating, cells were transduced with 100 MOI rAVCMV-LifeAct-TagRFP (ibidi).

Preparation of polyacrylamide coated plates.

Polyacrylamide (PA) gel coated plates were prepared following the protocol described previously25. Briefly, 30 mm glass-bottom plates (Greiner) were activated using 2% 3-aminopropyltrimethoxysilane, and 1% glutaraldehyde solution. Filtered polyacrylamide/bis-acrylamide 7.5/0.03% solution (Bio-Rad) was mixed with 0.02% suspension of carboxylated dark red fluospheres (Life Technologies), 0.05% ammonium persulphate and 0.4% temed (Bio-Rad). 7.5 μl of mixed PA solution was applied on each activated plate and covered with an 18 mm round glass cover slip to form a thin film. PA films were left to polymerize for 30 min at room temperature. Ultraviolet-activated Sulfo-SANPAH (Pierce Biotechnology) was used to couple 0.01% Poly-L-lysine (Sigma-Aldrich) to PA film. Finally, 20 μg ml−1 laminin (Sigma-Aldrich) was applied.

Spinning disc confocal microscopy.

Imaging was done using a Nikon Ti-E inverted microscope equipped with two Evolve EMCCD cameras (Photomatrix), four laser lines (405, 491, 561 and 642 nm), phase contrast and a Yokagawa spinning disc confocal scanner. The dish was maintained at 37 °C with 5% CO2/95% air using a cage incubator (Okolab). Imaging was done using a 40× 0.95 NA (air) PlanApo Lambda objective (Nikon). Fluo-4 was excited with a 491 nm laser (Cobolt), Fluorospheres were excited using a 642 nm laser (Vortran) and Lifeact-RFP was excited with a 561 nm laser (Cobolt). Stream acquisition (using Metamorph software) was performed before the application of the probe, during probe activation and for an hour after stopping the probe.

Mechanical probe.

A rigid tungsten probe with 25 μm tip diameter (Signatone) was mounted on a three-axis (X–Y –Z) micro-positioning stage (Thorlabs) installed on a custom-made adaptor for the microscope stage. The probe’s tip is immersed into the culture medium and slightly indents the PA substrate (2 μm indentation) 130 μm away from the target cell. The input is a sinusoidal waveform with an amplitude at the probe–gel contact point of 3–5 μm. Parameters were chosen to ensure that the deformations of the probe next to the edge of the cell equal the deformations made by the cell (see Supplementary Section 2 and Supplementary Figs 2–5 for further discussion). The deflection of the tungsten probe can be estimated as δmax = PL3/3EI, where P is the load acting on the probe, E = 411 GPa is the Young’s modulus of the probe and I is the area moment of inertia of a circular cross-section. The load due to substrate rigidity can be estimated using the elasticity of PA, EPA = 3.8 kPa and representative probe-generated strains. Owing to the high rigidity of the tungsten probe, the total deflection is smaller than one nanometre, which is negligible relative to the probe displacement.

Electrical field stimulation.

Cardiac cell culture was stimulated by electric field stimulation with a SIU-102 (Warner Instruments) using a RC37 chamber (Warner Instruments) mounted on an inverted Nikon spinning disc confocal set-up.

Data analysis.

Basic image analysis is done using ImageJ. Calcium profiles are further analysed using custom-written Matlab codes (FFT and Wavelet analysis). Mechanical deformations were analysed using a digital image processing (DIC) code26,27.

Atomic force microscopy.

Force curves were collected on JPK NanoWizard3 atomic force microscope. A silicon nitride cantilever with an attached 600-nm-diameter SiO2 particle tip (Novascan, Ames) was used to indent samples for collecting force curves. The spring constant of the cantilever was calculated to be 0.25 N m−1.