Abstract
A number of theories aiming at unifying gravity with other fundamental interactions, including field theory, suggest the violation of Lorentz symmetry1,2,3. Whereas the energy scale of such strongly Lorentz-symmetry-violating physics is much higher than that attainable at present by particle accelerators, Lorentz violation may nevertheless be detectable via precision measurements at low energies2. Here, we carry out a systematic theoretical investigation to identify which atom shows the greatest promise for detecting a Lorentz symmetry violation in the electron–photon sector. We found that the ytterbium ion (Yb+) is an ideal system with high sensitivity, as well as excellent experimental controllability. By applying quantum-information-inspired technology to Yb+, we expect tests of local Lorentz invariance (LLI) violating physics in the electron–photon sector to reach levels of 10−23—five orders of magnitude more sensitive than the current best bounds4,5,6.
Similar content being viewed by others
Main
It has been conjectured that Lorentz symmetry may be violated in string theories, with the Lorentz-violating effects being suppressed by some power of the ratio R between the electroweak scale and the natural (Planck) energy scale for strings: R = mew/Mpl = 2 × 10−17 (ref. 2). Therefore, the observable, but extremely small, Lorentz-violating effects may appear in low-energy experiments carried out with the corresponding high precision. Using the Yb+ ion, as proposed in this work, will for the first time allow probing whether Lorentz violation is minimally suppressed at low energies for photons and electrons. If the Lorentz violation is not observed in the Yb+ experiment proposed here, it will show that Lorentz violation in the photon–electron sector does not arise at this first-order level in strings, or cancellations are present between various Lorentz violation effects to nullify the combined result. With the proton and neutron tests already over the O(1) bound7,8,9, such a result would demonstrate that if physics at the Planck scale violates Lorentz invariance, it is more than minimally suppressed at low energies for normal matter, setting restrictions on potential unification theories.
Separate violations of LLI are possible for each type of particle, making it essential to verify LLI in different systems at a high level of precision. As a result, LLI tests have been conducted for photons5,10, protons7, neutrons8,9, electrons4,6, muons11 and neutrinos12, with the detailed summary of all current limits given in ref. 1.
Testing LLI of the electron motion in a Coulomb potential created by a nucleus has the appeal of testing for new physics in a well-understood system. In these atomic experiments4,6, one searches for variations of the atomic energy levels when the orientation of the electronic wavefunction is rotated with respect to the standard reference frame, such as the Sun-centred celestial-equatorial frame (SCCEF; ref. 13). The atomic experiments may be interpreted as Lorentz violation tests for the photon, electron, and nucleus constituents, such as the proton and neutron; with different experiments being sensitive to a different combination of LLI effects14. The most sensitive LLI tests for the electron have been conducted with neutral Dy atoms4 and Ca+ ions6. In this work, we explore the rest of the periodic table to answer the following question: which atomic system could most drastically improve tests of LLI in the electron–photon sector?
LLI-violating effects can be classified in the framework of the standard model extension (SME; refs 1,15,16). The SME is an effective field theory that maintains energy–momentum conservation, observer Lorentz covariance, and gauge invariance, but supplements the standard model Lagrangian with all combinations of the SM fields that are not term-by-term Lorentz invariant15,16. A particular advantage of the SME is the possibility to compare bounds on the Lorentz-violating parameters resulting from completely different experiments.
Here we focus on the term of the SME Lagrangian signifying the dependence of the maximally attainable velocity of a particle with respect to its propagation direction. We identify several factors that affect the precision of such a LLI test with atomic systems. First, it is crucial to use a state with a long lifetime to allow for a precise determination of the energy differences. Second, it is beneficial that the state has a strong sensitivity to LLI-violation effects in the electron–photon sector, that is, the size of the matrix element of the corresponding operator. The LLI-violating interaction6 contains the second power of the momentum operator p. Therefore, the corresponding matrix elements are expected to be large for orbitals with large kinetic energy. This happens for the atomic 4f-electrons localized deep inside the atom in the area of large potential and kinetic energy in some atomic systems. Last, we ask for a good theoretical understanding of the system and availability of already developed experimental techniques to carry out precision measurements.
We find that the metastable 4f136s2 2F7/2 state of Yb+ has extremely favourable characteristics, such as being very sensitive to LLI violations as well has having an exceptionally long lifetime—of the order of ten years (ref. 17). In addition, the experimental methods for Yb+ are well developed in the context of atomic clocks and the search for variation of fundamental constants. In particular, the electric-octupole E3 transition between the 4f136s2 2F7/2 excited state and the ground state18,19,20 has been studied in detail for these applications. Yb+ ions are also used in quantum information research21. As a result, the Yb+ ion is a well-studied system for precision control and manipulation of its atomic states, making it particularly well-suited to searches for the Lorentz violation signature.
The effect of various sources of Lorentz violation on atomic frequencies has been discussed in ref. 14. Here, we follow the formalism of ref. 6, in which a possible Lorentz violation in light manifests itself in the electronic SME Lagrangian, which is given by (in atomic units)

where ψ is a Dirac spinor, γμ are the Dirac matrices,  , with Dν being the covariant derivative. The tensor cμν′ = cμν + kμν/2 that characterizes the LLI-violation effects contains Lorentz-violation parameters from both the electron (cμν) and the photon (kμν) sectors1,2.
, with Dν being the covariant derivative. The tensor cμν′ = cμν + kμν/2 that characterizes the LLI-violation effects contains Lorentz-violation parameters from both the electron (cμν) and the photon (kμν) sectors1,2.
Experiments with 173Yb+ ions are also sensitive to violations of LLI for the neutron and the proton14,22. Moreover, the nucleus of 173Yb+ is deformed and has an order-of-magnitude enhanced electric quadrupole moment and time-reversal violating magnetic quadrupole moment as compared to a spherical nucleus23,24. A similar enhancement may exist for the nuclear LLI violation determined by the tensor 〈p2〉 −3〈pz2〉. Because we expect to surpass the energy resolution of 5 mHz for the proton test7 considerably, an experimental signature of LLI violation in a 173Yb+ experiment could come either from the electron–photon or the nuclear sector. The even Yb nuclei, which have zero nuclear spin and quadrupole moment, are not sensitive to violation of LLI of either protons or the neutron. Because the Yb+ LLI test involves monitoring quadrupole energy shifts, nuclear LLI effects will not contribute for the spin-1/2 nucleus 171Yb+, where nuclear LLI could produce only dipole energy shifts. Therefore, the electron/photon and nuclear sectors can be disentangled by comparing the LLI-violation signal from 173Yb+ with that of the other isotopes, resulting in clean LLI bounds.
From equation (1), violations of Lorentz invariance and Einstein’s equivalence principle in bound electronic states result in a small shift of the energy levels described by a Hamiltonian4,14

where p is the momentum of a bound electron, c is the speed of light, and U is the Newtonian gravitational potential. The parameters C0(0), c00 and C0(2) contain elements of the cμν′ tensor6. The relativistic form of the p2 operator is cγ0γjpj. The non-relativistic form of the T0(2) operator is T0(2) = p2 −3pz2, and the relativistic form is T0(2) = cγ0(γjpj −3γ3p3), with z (the third spatial component) defined by the quantization axis.
The cμν′ tensor is frame-dependent, but its value may be uniquely specified in the SCCEF (ref. 13). Because of the Earth’s motion, time-dependent Lorentz transformations from the SCCEF to the local laboratory frame give rise to time-dependence of the local observables that involve any of the C0(0), c00 and/or C0(2) parameters. The elements cJK in cμν′, where J, K = {1,2,3} (spatial components), which describe the dependence of the kinetic energy on the direction of the momentum, have a leading-order time-modulation period related to the sidereal day (12-h and 24-h modulation). Other elements, cTJ (where T = 0) and c00, describe the dependence of the kinetic energy on the boost of the laboratory frame, and have a leading-order time-modulation period related to the sidereal year.
The Yb+ ground state has the configuration [Xe]4f146s, and is essentially a heavier analogue of Ca+, which was used in the most recent experiment6, but has an additional set of states resulting from excitation of the filled 4f shell. Yb+ also has a metastable excited 5d5/2 state analogue to Ca+. However, the 4f shell in Yb+ is localized much deeper in the atom than the 6s or any other valence states, such as the 5d state. As a result, we expect the 4f136s2 2F7/2 metastable level of Yb+ to be very sensitive to Lorentz-violating effects. Indeed, we find that the LLI-sensitive T0(2) matrix element for this state is over an order of magnitude larger than for the 4f145d states (Methods). The results of the calculations are summarized in Table 1, where we also list reduced T(2) matrix elements defined in Methods for the nd states of Ca+, Ba+ and Yb+, which all have similar values.
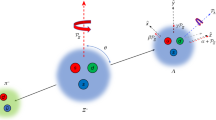
In a non-zero magnetic field, the excited state 4f136s2 2F7/2 of Yb+ will split into eight substates, with magnetic quantum numbers mJ = ±1/2, ±3/2, ±5/2, ±7/2 for even isotopes with no hyperfine structure. These four pairs of states will experience different energy shifts in the case of a detectable Lorentz-violation signal (see Fig. 1). The maximum Lorentz-violation signal will then be observed by monitoring the frequency difference between mJ = |1/2| and mJ = |7/2| states expressed in terms of the Lorentz-violating parameter C0(2) as

This gives an enhancement by a factor of 14 in comparison to Ca+ (ref. 6) owing to the increased T(2) matrix element.
The orthogonal orientations of the electronic wavefunction of the 4f136s2 2F7/2mJ manifold in Yb+, with mJ = |1/2| and mJ = |7/2|, will have a different response to the Lorentz-violating effect quantified by the cμν′ tensor. This results in a modulation of the energy difference between these two states as the Earth rotates the wavefunction with respect to the Sun-centred celestial-equatorial frame. The total electronic wavefunction is in superposition of the two states. The orientation of the wavefunction will be given by the direction of the magnetic field B, assumed to be fixed in the laboratory frame.
The odd 171Yb isotope has nuclear spin I = 1/2, leading to a splitting of the 4f136s2 2F7/2 level into two levels with total angular momenta F = 3 and F = 4 (Fig. 2). In a magnetic field, F = 3 level will split into seven sub-levels (mF = −3…3) and F = 4 level will split into nine sub-levels (mF = −4…4). The 173Yb isotope has nuclear spin I = 5/2, leading to more complicated level structure. For odd isotopes, the energy difference between magnetic hyperfine mF substates will be monitored.
Below, we discuss a procedure to detect potential LLI violations by measuring the energy difference between the mJ = |7/2| and mJ = |1/2| states in the 4f136s2 2F7/2 manifold in Yb+.
Typically, the main source of noise in such measurements is due to magnetic field fluctuations. To remove this noise, the work of ref. 6 used a superposition of two ions with a state prepared in a decoherence-free subspace (DFS; ref. 25). To implement the DFS technique with two trapped Yb+ ions, one will monitor the phase evolution difference of the state  , where |m1, m2〉 represents the state with mJ = m1 and m2 for the first and second ion, respectively, in the F7/2 manifold. The target state |Ψ〉 can be prepared by creating a product state, |ΨP〉 = (1/2)(|−1/2〉 + |−7/2〉) ⊗ (|+1/2〉 + |+7/2〉), which dephases into a mixed state that contains |Ψ〉 with 50% probability. With additional experimental complications, a direct preparation of an entangled state would result in an increase of the signal-to-noise ratio by a factor of two.
, where |m1, m2〉 represents the state with mJ = m1 and m2 for the first and second ion, respectively, in the F7/2 manifold. The target state |Ψ〉 can be prepared by creating a product state, |ΨP〉 = (1/2)(|−1/2〉 + |−7/2〉) ⊗ (|+1/2〉 + |+7/2〉), which dephases into a mixed state that contains |Ψ〉 with 50% probability. With additional experimental complications, a direct preparation of an entangled state would result in an increase of the signal-to-noise ratio by a factor of two.
Starting from the ground state of Yb+, the state  can be prepared with π/2 and π pulses using the coherent control developed for the implementation of the octupole 2S1/2–2F7/2 atomic clock18,19. Alternatively, one can also implement π/2 and π pulses by driving Raman transitions by means of the 2D5/2 state with 411 nm and 3.4 μm laser light (Fig. 2). For the odd 171Yb+ (inset in Fig. 2) and 173Yb+ isotope, one can prepare the target state with radiofrequency pulses, after populating a pure state in the 2F7/2 manifold.
can be prepared with π/2 and π pulses using the coherent control developed for the implementation of the octupole 2S1/2–2F7/2 atomic clock18,19. Alternatively, one can also implement π/2 and π pulses by driving Raman transitions by means of the 2D5/2 state with 411 nm and 3.4 μm laser light (Fig. 2). For the odd 171Yb+ (inset in Fig. 2) and 173Yb+ isotope, one can prepare the target state with radiofrequency pulses, after populating a pure state in the 2F7/2 manifold.
Another factor that will greatly improve the limits of the Lorentz-violating parameters obtained from measurements with Yb+ is the long lifetime of its excited state. In particular, because the lifetime of the 2F7/2 state of Yb+ is in the range of several years (ref. 20), the Ramsey duration of the proposed experiment with Yb+ is not limited by spontaneous decay. Instead, the coherence of the target state in the DFS is likely to be limited by the stability of the magnetic field gradient in the vicinity of the ions. It has been shown that in a magnetically unshielded environment, ions can retain entanglement in the DFS for up to 30 s (ref. 26). Hence, in a magnetically shielded trap, we can expect to suppress decoherence due to magnetic field noise such that Ramsey durations for much longer times are realistic.
An additional complication with long Ramsey interrogation times is that motional heating of the ion degrades the fidelity of the analysis pulses. For instance, the experiment in ref. 6 with 40Ca+ was performed with a Ramsey duration of 100 ms because of this motional heating. This problem can be either addressed with sympathetic cooling just before state read-out using auxiliary Yb ions, similar to preliminary work demonstrating this with 40Ca+ (ref. 27), or by employing ion traps providing sufficiently low motional heating rates, such as the ones typically used in quantum information processing experiments26.
We estimate that, with a Ramsey time of 60 s and two fully entangled Yb+ ions, the parameter C0(2) will be bounded at the level of  , where τ is the measurement time (Methods)—an improvement of ∼4,800 times over the measurement with 40Ca+ (ref. 6). At this level of sensitivity, we expect that the cJK parameters will be bounded at the level of 3 × 10−22 and 1.5 × 10−23 for a day-long and year-long measurement, respectively. The cTJ terms, which are sensitive to the velocity of the laboratory frame, are suppressed by a factor of 10−4 owing to the relatively small Earth’s velocity in the SCCEF as compared to the speed of light. With a year-long measurement, one expects to be sensitive to the cTJ parameters at the level of 1.5 × 10−19, a factor of 6,000 improvement over the current best limits4.
, where τ is the measurement time (Methods)—an improvement of ∼4,800 times over the measurement with 40Ca+ (ref. 6). At this level of sensitivity, we expect that the cJK parameters will be bounded at the level of 3 × 10−22 and 1.5 × 10−23 for a day-long and year-long measurement, respectively. The cTJ terms, which are sensitive to the velocity of the laboratory frame, are suppressed by a factor of 10−4 owing to the relatively small Earth’s velocity in the SCCEF as compared to the speed of light. With a year-long measurement, one expects to be sensitive to the cTJ parameters at the level of 1.5 × 10−19, a factor of 6,000 improvement over the current best limits4.
Systematics which can directly affect the energy of our target states are magnetic and electric field fluctuations in the vicinity of the ions. Both fields can be measured directly using the ions themselves as a probe. We can then correct for the effects of the differential linear Zeeman shift between the two ions due to a finite magnetic field gradient across the ion string, the quadratic Zeeman shift, and the Stark shift from the oscillating electric field from the trap. A change in the environmental temperature during the measurement can also affect the energy shift through the black-body radiation (BBR). The BBR shift between the two Zeeman states (mJ = 1/2 and mJ = 7/2) of the F7/2 manifold depends on the anisotropy of the BBR source. By assuming that the temporal temperature variation of the environment is less than 0.1 K, we estimate that, in the worst case scenario of a maximal anisotropy of 100%, the differential BBR shift between the two Zeeman states is ∼1 μHz (ref. 28), which affects the sensitivity of cJK at the 6 × 10−24 level. Finally, we estimate that the systematic error due to the AC-Stark effect of laser interaction is negligible for the proposed experiment (Methods).
Our calculations also identified general rules for the enhancement of the reduced matrix elements of the T(2) operator. We find that the only parameter that significantly affects the matrix elements leading to the tensor Lorentz violation sensitivity is the deeper localization of the probe electron where the kinetic energy p2/2 and T(2) ∝ p2 are larger. We find that an expectation value 〈ψ| r |ψ〉 < 0.8 a.u. of the corresponding electron is a good indicator of the large value of the T(2) matrix element. This condition is satisfied for the 4f hole states, such as the Yb+ state considered here, or for highly charged ions with nf valence electrons and charges of ∼15 (ref. 29). Such systems with configurations containing two 4f electrons or two 4f holes can have an extra enhancement by a factor of two, and a higher degree of ionization leads to a further increase in the T(2) matrix element values. Other lanthanide ions, for example the Tm+ ion with 4f136s ground state, may provide other potential candidates for Lorentz violation tests. We also considered the Th3+ ion owing to its 5f5/2 ground state. Laser cooling was demonstrated for this ion in ref. 30, but we find that the corresponding T(2) matrix element is more than a factor of three smaller than the one in Yb+. The 5f orbital here is a valence orbital rather than a hole in the filled shell; moreover the 4f electron is generally deeper localized than the 5f electron.
Owing to the increased sensitivity to LLI violation and long lifetime of the metastable F7/2 state of Yb+, we estimate that experiments can reach the sensitivities of 1.5 × 10−23 for the cJK parameters, improving the current best limits6 by more than a factor of 105. Moreover, the projected sensitivity of the cTJ parameters will be at the level of 1.5 × 10−19. In the electron–photon sector, this would for the first time probe all tensor Lorentz-violating elements below the ratio between the electroweak and Planck energy scales2.
Methods
Calculation of the matrix elements.
The calculations of the energy shift due to LLI violation reduce to a calculation of the expectation value of the Hamiltonian in equation (2). The matrix element of 〈JmJ| p2 −3pz2 |JmJ〉 is expressed through the reduced matrix element of the T(2) operator using the Wigner–Eckart theorem

Using the algebraic expression for the 3j-symbol, we arrive at the following expression for the matrix element of the 〈JmJ| p2 −3pz2 |JmJ〉 operator:

The angular factors are different for the Yb+4f136s2 2F7/2 state and the Ca+3d 2D5/2 state, resulting in total enhancement of the Yb+ LLI energy shift (equation (3)) of 13.8 in comparison with Ca+ case, whereas reduced matrix elements 〈J| |T(2)| |J〉 differ by a factor of 14.6.
The all-order method gave very accurate values of the 3dJ lifetimes31 and quadrupole moments32 in Ca+. In the all-order method, single, double, and partial triple excitations of Dirac–Hartree–Fock wavefunctions are included to all orders of perturbation theory. We refer the reader to review ref. 33 for the description of the all-order method and its applications. The Ca+ all-order results are accurate to about 1.5% (ref. 6). The calculations were carried out with both non-relativistic and relativistic operators; the differences were found to be negligible at the present level of accuracy. The results are listed inTable 2.
The all-order method was designed to work for monovalent systems and is not applicable to the calculation of 4f136s2 2F7/2 properties owing to the electronic configuration of this state, which has a hole in the 4f shell. We used both a one-electron Dirac–Fock calculation and a large-scale configuration interaction calculation for this state and find excellent agreement of both approaches. The 15-electron configuration interaction calculation follows the approach described in ref. 34. Briefly, we start from the solution of the Dirac–Fock equations and carry out the initial self-consistency procedure for the [1s2, …, 4f14, 6p] configuration. The 6s orbital was constructed for the 4f136s2 configuration, and the 5d3/2,5/2 orbitals were constructed for the 4f135d6s configuration. The basis set used in the CI calculations included virtual orbitals up to 8s, 8p, 7d, 7f and 5g. The virtual orbitals were constructed as described in refs 35,36. The configuration space was formed by allowing single and double excitations for the odd-parity states from the 4f146p, 4f136s2 and 4f135d6s configurations to virtual orbitals of the basis set listed above.
We have verified the convergence of the CI by carrying out three calculations with an increasing set of configuration functions: including single and double (SD) excitations to the 6s, 6p, 5d and 5f orbitals (we designate it [6sp5df]); adding excitations to the 7s, 7p, 6d, 6f and 5g orbitals [7sp6df5g]; and also adding 8s, 8p, 7d and 7f orbitals [8sp7df5g]. The last configuration set results in rather lengthy calculations with ∼2,300,000 determinants.
As demonstrated in Table 2, the number of included configurations has only a negligible effect on the T(2) operator of the 4f136s2 2F7/2 state. The result of the configuration interaction calculation is in agreement with a simple DF calculation. Inclusion of the random-phase approximation changes this value by 6%.
Estimation of the sensitivity of the experiment.
The sensitivity of the frequency variation can be estimated from the quantum projection noise of the measurement:

where A is the amplitude of the Ramsey oscillation signal, T is the Ramsey duration and τ is the measurement time. Assuming that the target state  for 2F7/2 is prepared through the creation of a mixed state, as demonstrated in ref. 6, then the amplitude of the Ramsey oscillation is A = 0.5. With a Ramsey duration of 60 s, the estimated sensitivity is
for 2F7/2 is prepared through the creation of a mixed state, as demonstrated in ref. 6, then the amplitude of the Ramsey oscillation is A = 0.5. With a Ramsey duration of 60 s, the estimated sensitivity is  . Together with the improved sensitivity of the atomic state to Lorentz violation, as given in equation (3), we estimate that the parameter C0(2) will be bounded at the level of
. Together with the improved sensitivity of the atomic state to Lorentz violation, as given in equation (3), we estimate that the parameter C0(2) will be bounded at the level of  for two ions, which is an improvement of ∼2,400 times over the measurement with 40Ca+ (ref. 6). Use of the pure entangled two-ion states (A = 1) would improve these bounds by an additional factor of two, resulting in a sensitivity of the C0(2) at the level of
for two ions, which is an improvement of ∼2,400 times over the measurement with 40Ca+ (ref. 6). Use of the pure entangled two-ion states (A = 1) would improve these bounds by an additional factor of two, resulting in a sensitivity of the C0(2) at the level of  —an improvement of ∼4,800 times over the measurement with 40Ca+ (ref. 6).
—an improvement of ∼4,800 times over the measurement with 40Ca+ (ref. 6).
Systematic effects due to the AC-Stark effect.
We now discuss the impact of the substantial AC-Stark shift when driving the weak octupole transition from the ground state to the 2F7/2 state. For instance, in the experiments in ref. 20, for each π pulse an AC-Stark-effect-related phase of the order of 2π × 3.3 rad was accumulated. However, for the odd Yb-isotopes the desired superposition state can be achieved by driving microwave transitions between hyperfine levels of the F7/2 manifold. Hence, driving the octupole transition (or alternatively the Raman transition via the D-states) is only required to populate a single Zeeman state of the F7/2 manifold as well as to probe for its population after the Ramsey sequence. Thus, the AC-Stark effect associated with driving the octupole transition has no impact on the actual phase evolution.
For the even isotopes it is possible to find state preparation schemes where the AC-Stark shift cancels between both ions, to the degree the ions are illuminated by the same amount. In such a scheme, the two ions would be prepared in the two distinct Zeeman states of the ground state, mJ = ±1/2. A common two-frequency laser field would prepare the desired superposition state on the different Zeeman transitions via the π/2 pulse driving the mJ = 1/2 → mJ = 7/2 transition on the first ion and the mJ = −1/2 → mJ = −1/2 transition on the second ion. The preparation concludes with a π pulse on the mJ = 1/2 → mJ = 1/2 transition on the first ion and the mJ = −1/2 → mJ = −7/2 transition on the second ion. This sequence leads to an equal phase due to the AC-Stark effect of the relevant |1/2, −1/2〉 and |7/2, −7/2〉 states, and hence the AC-Stark effect drops out. We estimate that using an intensity stability of 10−2 and illuminating both ions to within 10−3 equally will suppress the residual Stark-shift-related phase to 2π × 2 × 10−4 rad, well below the quantum projection noise of 100 experimental cycles of 2π × 1.6 × 10−2 rad, after which the intensities could be re-calibrated.
We conclude by stating that the expected AC-Stark effect when preparing the F7/2 with Raman transitions via the D-states requires less power than via the octupole transition, so the AC-Stark effect should pose no hurdle for this route either.
References
Kostelecký, V. A. & Russell, N. Data tables for Lorentz and CPT violation. Rev. Mod. Phys. 83, 11–32 (2011).
Kostelecký, V. A. & Potting, R. CPT, strings, and meson factories. Phys. Rev. D 51, 3923–3935 (1995).
Pospelov, M. & Shang, Y. Lorentz violation in Horava–Lifshitz-type theories. Phys. Rev. D 85, 105001 (2012).
Hohensee, M. A. et al. Limits on violations of Lorentz symmetry and the Einstein equivalence principle using radio-frequency spectroscopy of atomic dysprosium. Phys. Rev. Lett. 111, 050401 (2013).
Nagel, M. et al. Direct terrestrial test of Lorentz symmetry in electrodynamics to 10−18. Nature Commun. 6, 8174 (2015).
Pruttivarasin, T. et al. Michelson–Morley analogue for electrons using trapped ions to test Lorentz symmetry. Nature 517, 592–595 (2015).
Wolf, P., Chapelet, F., Bize, S. & Clairon, A. Cold atom clock test of Lorentz invariance in the matter sector. Phys. Rev. Lett. 96, 060801 (2006).
Allmendinger, F. et al. New limit on Lorentz-Invariance- and CPT-violating Neutron Spin interactions using a free-spin-precession 3He-129Xe comagnetometer. Phys. Rev. Lett. 112, 110801 (2014).
Smiciklas, M., Brown, J. M., Cheuk, L. W., Smullin, S. J. & Romalis, M. V. New test of local Lorentz invariance using a 21Ne–Rb–K comagnetometer. Phys. Rev. Lett. 107, 171604 (2011).
Eisele, Ch, Nevsky, A. Yu & Schiller, S. Laboratory test of the isotropy of light propagation at the 10−17 level. Phys. Rev. Lett. 103, 090401 (2009).
Bennett, G. W. et al. Muon g − 2 Collaboration. Search for Lorentz and CPT violation effects in muon spin precession. Phys. Rev. Lett. 100, 091602 (2008).
Adamson, P. et al. (The MINOS Collaboration) Search for Lorentz invariance and CPT violation with muon antineutrinos in the MINOS Near Detector. Phys. Rev. D 85, 031101 (2012).
Kostelecký, V. A. & Mewes, M. Signals for Lorentz violation in electrodynamics. Phys. Rev. D 66, 056005 (2002).
Kostelecký, V. A. & Lane, C. D. Constraints on Lorentz violation from clock-comparison experiments. Phys. Rev. D 60, 116010 (1999).
Colladay, D. & Kostelecký, V. A. CPT violation and the standard model. Phys. Rev. D 55, 6760–6774 (1997).
Colladay, D. & Kostelecký, V. A. Lorentz-violating extension of the standard model. Phys. Rev. D 58, 116002 (1998).
Roberts, M. et al. Observation of an electric Octupole transition in a single ion. Phys. Rev. Lett. 78, 1876–1879 (1997).
Huntemann, N. et al. Improved limit on a temporal variation of m p/m e from comparisons of Yb+ and Cs atomic clocks. Phys. Rev. Lett. 113, 210802 (2014).
Godun, R. M. et al. Frequency ratio of two optical clock transitions in 171Yb+ and constraints on the time variation of fundamental constants. Phys. Rev. Lett. 113, 210801 (2014).
Huntemann, N. et al. High-accuracy optical clock based on the octupole transition in 171Yb+. Phys. Rev. Lett. 108, 090801 (2012).
Islam, R. et al. Emergence and frustration of magnetism with variable-range interactions in a quantum simulator. Science 340, 583–587 (2013).
Stadnik, Y. V. & Flambaum, V. V. Nuclear spin-dependent interactions: searches for WIMP, axion and topological defect dark matter, and tests of fundamental symmetries. Eur. Phys. J. C 75, 110 (2015).
Flambaum, V. V. Spin hedgehog and collective magnetic quadrupole moments induced by parity and time invariance violating interaction. Phys. Lett. B 320, 211–215 (1994).
Flambaum, V. V., DeMille, D. & Kozlov, M. G. Time-reversal symmetry violation in molecules induced by nuclear magnetic quadrupole moments. Phys. Rev. Lett. 113, 103003 (2014).
Roos, C. F., Chwalla, M., Kim, K., Riebe, M. & Blatt, R. ‘Designer atoms’ for quantum metrology. Nature 443, 316–319 (2006).
Häffner, H. et al. Robust entanglement. Appl. Phys. B 81, 151–153 (2005).
Pruttivarasin, T. Spectroscopy, Fundamental Symmetry Tests and Quantum Simulation with Trapped Ions PhD thesis, Univ. California (2014).
Flambaum, V. V., Porsev, S. G. & Safronova, M. S. Energy shift due to anisotropic black body radiation. Preprint at http://arXiv.org/abs/1508.01242 (2015).
Safronova, M. S. et al. Highly-charged ions for atomic clocks, quantum information, and search for α-variation. Phys. Rev. Lett. 113, 030801 (2014).
Campbell, C. J. et al. Multiply charged thorium crystals for nuclear laser spectroscopy. Phys. Rev. Lett. 102, 233004 (2009).
Kreuter, A. et al. Experimental and theoretical study of the 3d2D − level lifetimes of 40Ca+. Phys. Rev. A 71, 032504 (2005).
Jiang, D., Arora, B. & Safronova, M. S. Electric quadrupole moments of metastable states of Ca+, Sr+, and Ba+. Phys. Rev. A 78, 022514 (2008).
Safronova, M. S. & Johnson, W. R. All-order methods for relativistic atomic structure calculations. Adv. At. Mol. Opt. Phys. 55, 050401 (2008).
Porsev, S. G., Safronova, M. S. & Kozlov, M. G. Correlation effects in Yb+ and implications for parity violation. Phys. Rev. A 86, 022504 (2012).
Bogdanovich, P. Usage of transformed functions for calculations of electric dipole transitions. Lith. Phys. J. 31, 79–83 (1991).
Kozlov, M. G., Porsev, S. G. & Flambaum, V. V. Manifestation of the nuclear anapole moment in the M1 transitions in bismuth. J. Phys. B 29, 689–697 (1996).
Acknowledgements
M.S.S. thanks the School of Physics at UNSW, Sydney, Australia for hospitality and acknowledges support from the Gordon Godfrey Fellowship programme, UNSW. This work was supported by the NSF CAREER Program grant #PHY 0955650, NSF grants # PHY 1212442, #PHY 1404156, #PHY 1507160 and #PHY 1520993, the Australian Research Council and was performed under the auspices of the US Department of Energy by Lawrence Livermore National Laboratory under Contract DE-AC52-07NA27344. T.P. is supported by RIKEN’s Foreign Postdoc Researcher Program.
Author information
Authors and Affiliations
Contributions
V.A.D. had the idea to use Yb+ and identified the enhancement to the Lorentz violation violation. V.A.D., V.V.F., M.S.S. and S.G.P. carried out atomic calculations. T.P., M.A.H. and H.H. worked out the experimental scheme considerations and projected the Lorentz violation limits. All authors contributed to the discussions of the results and manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
About this article
Cite this article
Dzuba, V., Flambaum, V., Safronova, M. et al. Strongly enhanced effects of Lorentz symmetry violation in entangled Yb+ ions. Nature Phys 12, 465–468 (2016). https://doi.org/10.1038/nphys3610
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys3610
This article is cited by
-
Improved bounds on Lorentz violation from composite pulse Ramsey spectroscopy in a trapped ion
Nature Communications (2022)
-
Influences of Lorentz symmetry violation on charged Dirac fermions in cosmic dislocation space-time
General Relativity and Gravitation (2022)
-
Point-to-point stabilized optical frequency transfer with active optics
Nature Communications (2021)
-
Free-space transfer of comb-rooted optical frequencies over an 18 km open-air link
Nature Communications (2019)
-
Optical clock comparison for Lorentz symmetry testing
Nature (2019)