Abstract
The origin of heavy elements produced through rapid neutron capture (‘r-process’) by seed nuclei is one of the current nucleosynthesis mysteries1,2,3. Core collapse supernovae (cc-SNe; ref. 4) and compact binary mergers are considered as possible sites5,6,7. The first produces small amounts of material at a high event rate whereas the latter produces large amounts in rare events. Radioactive elements with the right lifetime can break the degeneracy between high-rate/low-yield and low-rate/high-yield scenarios. Among radioactive elements, most interesting is 244Pu (half-life of 81 million years), for which both the current accumulation of live 244Pu particles accreted via interstellar particles in the Earth’s deep-sea floor8 and the Early Solar System (ESS) abundances have been measured9. Interestingly, the estimated 244Pu abundance in the current interstellar medium inferred from deep-sea measurements is significantly lower than that corresponding to the ESS measurements. Here we show that both the current and ESS abundances of 244Pu are naturally explained within the low-rate/high-yield scenario. The inferred event rate remarkably agrees with compact binary merger rates estimated from Galactic neutron star binaries10 and from short gamma-ray bursts11. Furthermore, the ejected mass of r-process elements per event agrees with both theoretical12,13,14 and observational15,16,17 macronova/kilonova estimates.
Similar content being viewed by others
Main
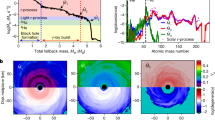
Using the Solar abundance19 as the mean value for stars in the Galactic disk, the total mass of heavy r-process elements (A ≥ 90) in the Galaxy is Mtot, A≥90 ≈ 5 × 103M⊙. These elements show a consistent abundance pattern in metal-poor stars18, suggesting that they are produced in a single kind of event. The total mass yields a relation between the Galactic event rate, R, and the heavy r-process mass produced in each event Mej, A≥90 (see Fig. 1):

Here 〈R〉 is the rate averaged over the age of the Galaxy and it is not necessarily the same as the present-day event rate R0. For sources related to the death of massive stars, the event rate should follow the star formation rate, which at present is lower than the average value20. For compact binary mergers, the event rate follows the star formation rate with some delay. The event rate of short gamma-ray bursts (SGRBs) (ref. 11) that probably arise from compact binary mergers6, increases with the cosmological redshift z at least up to z ≈ 0.8. In both cases, R0 may be smaller than 〈R〉 by a factor of up to approximately five.
The diagonal green region expresses the degeneracy between high rate/low yield and low rate/high yield corresponding to the total mass of (stable) heavy (A ≥ 90) r-process elements in the Galaxy, with R0 = 〈R〉, 0.5〈R〉, and 0.2〈R〉 (see equation (1)). The allowed region inferred from the 244Pu abundance in the deep-sea crust8 and the ESS (refs 9,23) is shown as a blue band. The blue solid (dotted) line corresponds to the current ISM 244Pu density being the median (2σ) value. The region above the dashed blue curve is the allowed region consistent with the ESS measurement (within 2σ fluctuations and taking into account that the rate at 4.6 Gyr BP can be higher than R0 by up to a factor of five). The current event rate estimated from binary neutron stars10 and SGRBs (ref. 11) are shown as the region between the horizontal red lines. For SGRBs, we take an (unknown) jet beaming factor in the range of 10–70. The region between the horizontal dotted purple lines corresponds to the cc-SNe event rate29. Macronova mass estimates12,13,14,15,16,17 are between the vertical dark orange lines. The upper and lower horizontal arrows, respectively, show the LIGO/Virgo upper limit of the merger rate30 and the expected capability of the advanced gravitational-wave detectors with 5 yr observations. The overlap region of the 244Pu measurements and the total amount of heavy r-process elements is consistent with that of the compact binary merger scenario.
Using the total mass alone we cannot distinguish between the high-rate/low-yield and the low-rate/high-yield sources. Measurements of abundances of short-lived radioactive r-process nuclides can, however, remove this degeneracy, as these abundances reflect the r-process production history on timescales comparable to their lifetimes (modulo the Galactic mixing timescale). Among the various radioactive nuclides, 244Pu seems most suitable: it is produced only via the r-process; the half-life of 244Pu, 81 Million years (Myr), is sufficiently short compared to the Hubble time, although long enough to allow for significant accumulation; and both current and ESS (∼4.6 Gyr before present; BP) 244Pu abundance in the interstellar medium (ISM) have been measured.
The inner Solar System continuously accretes interstellar dust grains21 containing recently produced live radioactive 244Pu. Wallner et al. 8 (see also Paul et al. 22) measured the accumulation of 244Pu in a deep-sea crust sample during the past 25 Myr and estimated the 244Pu flux on the Earth’s orbit as 250−205+590 cm−2 Myr−1, where the upper and lower values correspond to 2σ limits. The corresponding mean number density of 244Pu in the ISM is 6 × 10−17 cm−3 and the 2σ upper limit is 2 × 10−16 cm−3 (see Supplementary Methods). These values are significantly lower than the number density in the ISM derived from the ESS 244Pu abundance: nPu ≈ (244Pu/238U)ESSYU, ESSnISM ∼ 6 × 10−15 cm−3. The relative abundance ratio of (244Pu/238U)ESS ≈ 0.008 is estimated from fissiogenic xenon in ESS relics9 (for example, chondritic meteorites). YU, ESS = 7.3 × 10−13 is the number abundance of 238U relative to hydrogen inferred from meteorites23 (corrected from the present for 238U decay) and nISM is the mean number density of the ISM, which is typically approximately 1 cm−3.
The abundance of a radioactive nuclide at a given location around the solar circle, r⊙, depends on the event rate density,  , where ρ∗(r, z) is the stellar mass density in the disk, r and z are the Galactic radius and height above the Galactic plane, and M∗ is the total stellar mass in the disk24. The abundance depends also on the mixing rate. The most relevant mixing process is turbulent diffusion (see Supplementary Methods) whose diffusion coefficient satisfies D = αvtH ≈ α kpc2/Gyr (vt/7 km s−1)(H/0.2 kpc), where vt is the typical turbulence velocity of the ISM, H is the ISM scale height, and α is the mixing length parameter. Defining τmix as the mean time between injection events at a given location which satisfies
, where ρ∗(r, z) is the stellar mass density in the disk, r and z are the Galactic radius and height above the Galactic plane, and M∗ is the total stellar mass in the disk24. The abundance depends also on the mixing rate. The most relevant mixing process is turbulent diffusion (see Supplementary Methods) whose diffusion coefficient satisfies D = αvtH ≈ α kpc2/Gyr (vt/7 km s−1)(H/0.2 kpc), where vt is the typical turbulence velocity of the ISM, H is the ISM scale height, and α is the mixing length parameter. Defining τmix as the mean time between injection events at a given location which satisfies  , we derive:
, we derive:

The median number density (the median rather than the average reflects the density that a typical observer measures) of a short-lived radioactive nuclide with a mean-life τi is:

where  is the equilibrium value and Ni is the total number of the nuclide i ejected by each event. For τi ≫ τmix, a typical observer measures neq, i. For τi ≪ τmix, a typical observer measures a number density much lower than neq, i and one needs a larger yield to reach an observed value, interpreted here as the median number density. Figure 1 depicts the needed rate and yield so that the current 244Pu number density is the median value for typical values of α, vt and H (see equation (2)). This relation (blue area in Fig. 1) becomes flatter than R ∝ Mej−1 (equation (1), green band in Fig. 1) for decreasing event rates breaking the rate-yield degeneracy.
is the equilibrium value and Ni is the total number of the nuclide i ejected by each event. For τi ≫ τmix, a typical observer measures neq, i. For τi ≪ τmix, a typical observer measures a number density much lower than neq, i and one needs a larger yield to reach an observed value, interpreted here as the median number density. Figure 1 depicts the needed rate and yield so that the current 244Pu number density is the median value for typical values of α, vt and H (see equation (2)). This relation (blue area in Fig. 1) becomes flatter than R ∝ Mej−1 (equation (1), green band in Fig. 1) for decreasing event rates breaking the rate-yield degeneracy.
To take into account the large fluctuation in the measured number density averaged over timescales shorter than τmix, we simulate the history of the 244Pu abundance in the ISM around the solar circle over the past 7 Gyr. We take into account the radioactive decay, the turbulent diffusion process and the time evolution of the production rate. We consider here a characteristic low-rate/high-yield case of R0 = 5 Myr−1 following the SGRB rate11 evolution and a high-rate/low-yield case of R0 = 300 Myr−1 following the cosmic star formation history20 (Fig. 2). As expected the fluctuations of the low-rate/high-yield case are much larger than those of the high-rate/low-yield case. For both cases, the estimated range of number densities around 4.6 Gyr BP are consistent with the ESS values and they decrease with time following the decreasing event rate. Whereas for R0 = 5 Myr−1 the simulated values are also consistent with the current deep-sea measurements, for R0 = 300 Myr−1 the decline is insufficient even when taking the fluctuations into account. Figure 1 depicts upper and lower bounds on the event rate which consistently explain the 244Pu abundance of the ESS and the current ISM. The sources must satisfy R0 ≤ 90 Myr−1 and Mej ≥ 0.001 M⊙. Although these limits vary slightly with different assumed parameters (see Supplementary Methods), the qualitative result that we reach is robust and independent of these choices. We conclude that unless an unidentified process suppresses the present amount of 244Pu that reaches Earth, the heavy r-process sources are dominantly low-rate/high-yield ones. The rarity of r-processing events also consistently explains the large scatter in r-elements/Fe abundance of metal-poor stars25,26,27,28.
The solid red (blue) lines represent the median number density and ±1σ fluctuations for R0 = 5 Myr−1 (R0 = 300 Myr−1). The lower square with an error bar shows the 244Pu density with 2σ limits inferred from the deep-sea measurement8. The triangle at 4.6 Gyr BP shows the value at the time of the ESS (refs 9,23). The production rate of 244Pu follows the time evolution of the SGRB rate11 for R0 = 5 Myr−1 and the cosmic star formation history20 for R0 = 300 Myr−1. Also shown is a Monte Carlo simulation the time sequence of 244Pu number densities at a given location on the solar circle for R0 = 5 Myr−1 (dotted red line) and R0 = 300 Myr−1 (dotted blue line).
These results are compared with astronomical observations concerning the possible sources. The low rate clearly rules out cc-SNe. The current 244Pu abundance should be larger by a factor of 5–100 to be compatible with a dominant cc-SNe source (see Supplementary Methods). Turning to compact binary mergers, Fig. 1 depicts also the merger rate estimated from known Galactic binary neutron stars10 and from the current SGRB rate11, as well as the ejected mass of r-process elements estimated from macronova candidates associated with GRB 130603B (refs 15,16) and with GRB 060614 (ref. 17). Remarkably, the rates and masses estimated here are fully consistent with those observations. In fact most of the overlap between the allowed 244Pu region and the overall r-process production range is just in this part of the astrophysical parameter phase space describing compact binary mergers and macronova ejection estimates. This result is independent of the choice of the efficiency and diffusion parameters.
Compact binary mergers, which we can conclude are the sources of heavy r-process nucleosynthesis, are also the prime candidates of sources for the gravitational-wave detectors, advanced LIGO/Virgo and KAGRA. Our estimates provide an upper limit to the expected detection rate (assuming a detection horizon distance of 200 Mpc): RGW ≤ 30 yr−1. The estimated ejected mass in each event is significant, implying that macronovae31,32,33 and radio flares34 associated with the gravitational-wave merger events will be detectable with follow-up observations.
References
Cowan, J. J., Thielemann, F.-K. & Truran, J. W. The R-process and nucleochronology. Phys. Rep. 208, 267–394 (1991).
Qian, Y.-Z. & Wasserburg, G. J. Where, oh where has the r-process gone? Phys. Rep. 442, 237–268 (2007).
Arnould, M., Goriely, S. & Takahashi, K. The r-process of stellar nucleosynthesis: Astrophysics and nuclear physics achievements and mysteries. Phys. Rep. 450, 97–213 (2007).
Burbidge, E. M. et al. Synthesis of the elements in stars. Rev. Mod. Phys. 29, 547–650 (1957).
Lattimer, J. M. & Schramm, D. N. Black-hole–neutron-star collisions. Astrophys. J. Lett. 192, L145–L147 (1974).
Eichler, D. et al. Nucleosynthesis, neutrino bursts and gamma-rays from coalescing neutron stars. Nature 340, 126–128 (1989).
Freiburghaus, C., Rosswog, S. & Thielemann, F.-K. R-Process in neutron star mergers. Astrophys. J. 525, L121-L124 (1999).
Wallner, A. et al. Abundance of live 244Pu in deep-sea reservoirs on Earth points to rarity of actinide nucleosynthesis. Nature Commun. 6, 5956 (2015).
Turner, G. et al. Pu Xe, U Xe, U Pb chronology and isotope systematics of ancient zircons from Western Australia. Earth Planet. Sci. Lett. 261, 491–499 (2007).
Kim, C., Perera, P. B. B. & McLaughlin, M. A. Implications of PSR J0737-3039B for the Galactic NS-NS binary merger rate. Mon. Not. R. Astron. Soc. 448, 928–938 (2015).
Wanderman, D. & Piran, T. The rate luminosity function and time delay of non-collapsar short GRBs. Mon. Not. R. Astron. Soc. 448, 3026–3037 (2015).
Rosswog, S. The dynamic ejecta of compact object mergers and eccentric collisions. Phil. Trans. R. Soc. A 371, 20120272 (2013).
Hotokezaka, K. et al. Mass ejection from the merger of binary neutron stars. Phys. Rev. D 87, 024001 (2013).
Bauswein, A., Goriely, S. & Janka, T.-H. Systematics of dynamical mass ejection, nucleosynthesis, and radioactively powered electromagnetic signals from neutron-star mergers. Astrophys. J. 773, 78 (2013).
Tanvir, N. R. et al. A ‘kilonova’ associated with the short-duration γ-ray burst GRB130603B. Nature 500, 547–549 (2013).
Berger, E., Fong, W. & Chornock, R. An r-process kilonova associated with the short-hard GRB 130603B. Astrophys. J. Lett. 744, L23 (2013).
Yang, B. et al. A possible macronova in the late afterglow of the long-short burst GRB 060614. Nature Commun. 6, 7323 (2015).
Sneden, C., Cowan, J. J. & Gallino, R. Neutron-capture elements in the early galaxy. Annu. Rev. Astron. Astrophys. 46, 241–288 (2008).
Goriely, S. Uncertainties in the solar system r-abundance distribution. Astron. Astrophys. 342, 881–891 (1999).
Hopkins, A. M. & Beacom, J. F. On the normalization of the cosmic star formation history. Astronphys. J. 651, 142–154 (2006).
Mann, I. Interstellar dust in the solar system. Annu. Rev. Astron. Astrophys. 48, 173–203 (2010).
Paul, M. et al. Experimental limit to interstellar 244Pu abundance. Astrophys. J. Lett. 558, L133–L135 (2001).
Lodders, K., Palem, H. & Gail, H.-P. Abundances of the Elements in the Solar System (Landolt Börnstein Series 44, Springer, 2009).
McMillan, P. J. Mass models of the Milky Way. Mon. Not. R. Astron. Soc. 414, 2446–2457 (2011).
Cescutti, G. et al. The role of neutron star mergers in the chemical evolution of the Galactic halo. Astron. Astrophys. 577, A139 (2015).
Wehmeyer, B., Pignatari, M. & Thielemann, F.-K. Galactic evolution of rapid neutron capture process abundances: The inhomogeneous approach. Mon. Not. R. Astron. Soc. 452, 1970–1981 (2015).
Shen, S. et al. The history of R-process enrichment in the Milky Way. Astrophys. J. 807, 115 (2015).
van de Voort, F. et al. Galactic r-process enrichment by neutron star mergers in cosmological simulations of a Milky Way-mass galaxy. Mon. Not. R. Astron. Soc. 447, 140–148 (2015).
Li, W. et al. Nearby supernova rates from the Lick Observatory supernova search—III. The rate-size relation, and the rates as a function of galaxy Hubble type and colour. Mon. Not. R. Astron. Soc. 412, 1473–1507 (2011).
Abadie, J. et al. Search for gravitational waves from low mass compact binary coalescence in LIGO’s sixth science run and Virgo’s science runs 2 and 3. Phys. Rev. D 85, 082002 (2012).
Li, L.-X. & Paczyński, B. Transient events from neutron star mergers. Astrophys. J. Lett. 507, L59–L62 (1998).
Barnes, J. & Kasen, D. Effect of a high opacity on the light curves of radioactively powered transients from compact object mergers. Astrophys. J. 775, 18 (2013).
Tanaka, M. & Hotokezaka, K. Radiative transfer simulations of neutron star merger ejecta. Astrophys. J. 775, 113 (2013).
Nakar, E. & Piran, T. Detectable radio flares following gravitational waves from mergers of binary neutron stars. Nature 478, 82–84 (2011).
Acknowledgements
We gratefully acknowledge useful discussions with M. Eichler, K. Kashiyama, H. Kimura, E. Nakar, A. Wallner and D. Wanderman. This work was supported by the ISF I-Core Center for Excellence in Astrophysics, by a CNSF-ISF grant and by a grant from ISA.
Author information
Authors and Affiliations
Contributions
K.H. performed the calculations and produced the figures of the paper. T.P. contributed to all aspects of astrophysical discussions. M.P. contributed to the interpretation and discussion of the experimental data of the 244Pu abundance. All authors contributed to the writing of the paper.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary information
Supplementary information (PDF 3253 kb)
Rights and permissions
About this article
Cite this article
Hotokezaka, K., Piran, T. & Paul, M. Short-lived 244Pu points to compact binary mergers as sites for heavy r-process nucleosynthesis. Nature Phys 11, 1042 (2015). https://doi.org/10.1038/nphys3574
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys3574
This article is cited by
-
The production of actinides in neutron star mergers
AAPPS Bulletin (2022)
-
A nearby neutron-star merger explains the actinide abundances in the early Solar System
Nature (2019)
-
Neutron stardust and the elements of Earth
Nature Chemistry (2019)
-
Origin of the heavy elements in binary neutron-star mergers from a gravitational-wave event
Nature (2017)
-
Kilonovae
Living Reviews in Relativity (2017)