Main

Nd2Ir2O7 belongs to the family of pyrochlore iridates6,7,8,9, which have attracted a great deal of interest due to the combination of strong spin–orbit coupling and electronic correlations, which might hypothetically lead to various topological phases such as a topological Mott insulator, Weyl semimetal and axion insulator10,11,12,13,14. In fact, recent experiments observed a chiral spin liquid state and quantum critical semimetallic state in Pr2Ir2O7 (refs 6,7,8), as well as continuous MITs and all-in–all-out (AIAO) ordering in Nd2Ir2O7 (ref. 4) and Eu2Ir2O7 (ref. 9).

Comprehensive surveys of the R2Ir2O7 compounds show a systematic decrease in the thermal MIT temperature with increasing ionic radius of R, reaching zero ‘between’ R = Nd and Pr, so that Nd2Ir2O7 is the closest insulator to the T = 0 quantum MIT. Indeed, Nd2Ir2O7 shows an apparently continuous MIT at TMI ∼ 32 K, which is exceptionally low, especially relative to the gap Eg ∼ 45 meV observed experimentally5, leading to the unusually large ratio Eg/TMI ∼ 16. Recent neutron diffraction experiments suggest that in the low-temperature phase both the Nd3+ and the Ir4+ moments have an AIAO magnetic structure, an Ising type order with all the moments pointing inward or outward from the centre of each tetrahedron (Fig. 1a)15. What made this compound even more interesting is the recent proposal that this AIAO state may stabilize a Weyl semimetallic state10,11,12,13,14,16, raising the question of the nature of the MIT proximate to such topological phenomena.

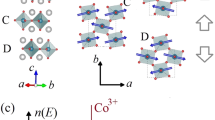
Figure 1: Thermal metal–insulator transition (MIT) in a Nd2Ir2O7 single crystal.
figure 1

a, Two domain spin structures for the all-in–all-out state. b, Temperature dependence of the zero-field resistivity ρ(T) measured on heating. The open circles and solid line denote the resistivity obtained in the zero-field-cooled (ZFC) and field-cooled (FC, 9 T) sequences, respectively, with the B ‖ [111] direction. The FC results have higher resistivity as it stabilizes a single magnetic domain below the transition temperature TMI. Inset shows the T derivative of ρ(T) at approximately TMI = 27 K (arrow). c, Temperature dependence of the magnetic susceptibility χ ≡ M/B of Nd2Ir2O7 single crystal obtained under a field of 0.01 T along the [001], [110] and [111] directions. The susceptibility obtained under the ZFC and FC sequences is shown. Inset indicates that the bifurcation of the ZFC and FC data starts below ∼TMI.

Full size image

First we describe the key experimental observations to verify the MIT in our single crystals of Nd2Ir2O7. The temperature dependence of the resistivity exhibits a MIT at TMI ∼ 27 K under zero field (Fig. 1b). This transition temperature is slightly lower than the value ∼32 K observed in polycrystalline samples, most likely as a result of carrier doping by slight off-stoichiometry within 1% (see Methods). Below TMI, ρ(T) shows insulating (negative dρ/dT) behaviour (Fig. 1b inset). It is known that the AIAO magnetic order sets in concomitantly with the MIT (ref. 4). Indeed, exactly below TMI ∼ 27 K, we found that the zero-field-cooled (ZFC) and field-cooled (FC) magnetization bifurcate owing to the magnetic transition (Fig. 1c).

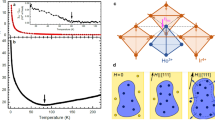
Now, we discuss our main discovery of the field-induced MIT and strongly anisotropic magnetoresistance. Figure 2a presents the angle dependence of the transverse magnetoresistance measured using pulsed high magnetic fields up to 50 T and a Nd2Ir2O7 single crystal with zero-field TMI ∼ 20 K. Here we note that to reveal the field evolution of the continuous MIT peculiar to the Ir 5d bands, a single crystal with TMI > 15 K is indispensable, as on cooling Nd moments freeze below 15 K (ref. 15). The field B was rotated within the (001) plane, perpendicularly to the current direction [], with the angle (θ) between the field and the [001] direction, as schematically shown in Fig. 2b inset. In this definition, θ = 35°, 55° and 90° correspond to the field direction of [112], [111] and [110] axes, respectively. In the field along these three directions, only a gradual decrease of the resistivity was found, revealing that the insulating state is stable up to 50 T. In sharp contrast, in the [001] direction, a rapid jump of the resistivity was observed at a critical field of Bc ∼ 10 T, above which the resistivity becomes nearly constant. The magnetoresistance [R(0) − R(B)]/R(B) amounts to ∼60,000%. This sharp resistivity drop characterizes the field-induced quantum phase transition to the high-B semimetal state. This high-field-induced semimetal state is also consistent with the temperature-dependent resistivity measurement, as shown in the inset of Fig. 2c. The narrow but clear hysteresis (∼1 T) seen at the critical field indicates that the transition is first order, despite the fact that the thermal transition at zero field is continuous.

Figure 2: Field-induced metal–insulator transition (MIT) of Nd2Ir2O7 observed using the pulsed magnetic field.
figure 2

A Nd2Ir2O7 single crystal with zero-field TMI ∼ 20 K was used. a, Field-dependent magnetoresistivity obtained with both increasing and decreasing field at T = 2 K for various field directions between [001] and [110]. The angle Θ is measured from the [001] direction as shown in b. b, Field–angle phase diagram based on the contour plot of the magnetoresistivity shown in a, and the angle dependence of the resistivity. The MIT critical field (open circle) is shown for the field where the resistivity merges with the nearly constant resistivity ∼2 mΩ cm of the high-field semimetallic phase. The inset indicates the geometric configuration for the measurements. c, Field dependence of the magnetoresistivity obtained at various temperatures with decreasing B ‖ [001]. Inset, temperature dependence of the resistivity measured on cooling under various d.c.-fields along the [001] direction. d, Temperature–field phase diagram for Nd2Ir2O7 under a magnetic field along the [001] direction. The MIT critical temperatures obtained on heating and cooling are shown respectively by red and orange diamond symbols, and the critical fields for increasing and decreasing field are shown by red and orange circles (Supplementary Information). A tricritical point separating the second- and first-order transition should exist between 2 and 6 T and approximately 18 K.

Full size image

To map out the interpolation between these limits, we show a selection of both the resistivity versus field and temperature at various temperatures and field in Fig. 2c, and its inset, respectively. Summarizing all the results, we construct a contour plot of the resistivity in the B–T phase diagram in Fig. 2d. We see that the enhanced resistivity is confined to a region of low B and T, and outside this region the resistivity is only weakly dependent on B and T. Thus, there are simply two phases: a resistive ordered antiferromagnetic state at low B and T, and a semimetallic paramagnetic state outside the ordered region (Fig. 2d). To characterize the thermal phase transition, we took the temperature derivative of the resistivity dρ/dT (Supplementary Information). For B = 0, 2 T, both dρ/dT taken on cooling and warming across TMI nearly overlap each other, indicating a second-order transition, whereas above 6 T they show clear hystereses across TMI due to the first-order character of the transition. This is consistent with the hysteresis seen in the field-dependent data shown in Fig. 2a and Supplementary Fig. 2. The MIT temperatures TMI and critical fields BMI are determined for both increasing (red diamond and circle) and decreasing (orange diamond and circle) sequences of temperature and field and are summarized in the phase diagram of Fig. 2d. This indicates that the tricritical point separating the second- and first-order transition exists between 2 and 6 T and approximately 18 K (Fig. 2d).

The strongly anisotropic character of the MIT can be seen from the field-angle phase diagram made by the contour plot of the resistivity (Fig. 2b). The full angle dependence shows that the field-induced transition survives when the magnetic field is slightly tilted from the [001] direction towards [112], by up to θ < 15°, but the critical field increases rapidly with θ. The strong anisotropy is also evident in the isothermal magnetization measured at 2 K (Fig. 3a). In particular, a large hysteresis was observed for B ‖ [111], whereas M(B) is smooth for B ‖ [001] and [110]. The field derivative of the [111] magnetization curve reveals two distinct kinks, at approximately Bc1 = 2.0 T and Bc2 = 3.9 T (Fig. 3b). Naively, these are suggestive of Nd3+ spin flops (the Ir moments are negligibly small on this scale17), which would arise in a classical ‘spin-ice’-like Ising model18. Such a model (using the single-ion moment 2.4 μB/Nd) predicts saturation at 1.4, 1.2 and 0.98μB/Nd for B along [001], [111] and [110], consistent with 1.4, 1.2 and 1.1μB/Nd in experiment. However, the smoothness of the sweeps for the [001] and [110] field orientations, as well as the fact that the down-sweep sequence shows no anomaly and reaches zero magnetization at zero field, are inconsistent with classical Ising spins.

Figure 3: Field-induced magnetic transition in Nd2Ir2O7.
figure 3

a, d.c.-magnetization at 2 K versus d.c.-field along the [111], [110] and [001] directions. Only for the [111] direction is a clear hysteresis seen after the field cycle. b, Field derivative of the [111] magnetization measured at T = 2 K. c, Magnetoresistivity at 2 K in the field along the [111] direction. The arrows indicate the field cycle direction.

Full size image

We now discuss Nd2Ir2O7 theoretically, as a nearly critical Kondo lattice system with a particular hierarchy of energy scales. The largest energies are electronic, with bare local density approximation (LDA) bandwidths of the order of 0.5 eV for the j = 1/2-like bands near the Fermi energy and Hubbard U of the order of 1–2 eV. The Kondo interaction between Nd and Ir spins is at a much lower energy scale, of the order of JK ∼ 5–10 meV (see below). However, a large reduction of the effective bandwidth may occur due to correlations and proximity to the zero-field quantum MIT, as indicated by recent ARPES experiments19. This opens a window unique to Nd2Ir2O7 where the Kondo coupling can influence the MIT.

We consider a model Hamiltonian H = HIr + HNd, where HIr includes all terms containing only Ir electrons, and HNd contains the Kondo interaction of overall strength JK and the Zeeman term for Nd (see below). Details of the Hamiltonians are given in Supplementary Information.

The problem for JK = B = 0 has been studied by mean-field theory12, LDA + U (refs 10,20), dynamical mean field theory (DMFT; refs 20,21), and by field theory methods22. All methods agree that with increasing U a non-magnetic ground state gives way at U > Uc to an AIAO ordered state, which has a spectral gap for large enough U. The critical value Uc is of the order of 1 eV, and varies according to band parameters and approximation methods. For fixed U > Uc, the AIAO ordered state is favourable relative to the non-magnetic state by a condensation energy that varies from Ec ∼ 100 meV to 15 meV depending on the method.

Now let us consider the role of Nd moments by turning on Jk. According to the crystal electric field scheme obtained experimentally, Nd3+ has a ‘dipolar–octupolar’ ground doublet, which can be represented by a vector Pauli spin operator τi, but which has an infinitely anisotropic g-tensor: its moment lies exactly along its local 〈111〉 axis. Accordingly, the full form of HNd allowed by symmetry is

where Si is the Ir spin at site i, is a unit vector along the local 〈111〉 axis of Nd site j, and γ = 2.4μB, up to weaker direct exchange interactions between Nd spins. Note that the Kondo couplings, described by the matrix Λ (Supplementary Information) involve all components of the Nd spin, but we expect those involving the local z component τz dominate in most circumstances. An exception is in the evolution of the spin state from low to intermediate fields (∼10 T): there, the non-Ising interactions allow the Nd spins to rotate smoothly rather than flop, except when the field is along the [111] direction, which explains the main features of Fig. 3b, c (Supplementary Information).

To JK-linear order, we can treat the Kondo interaction in mean field, as effective self-consistent static fields on the Nd and Ir spins. At zero field, this aligns the Nd spins into an AIAO state, and splits the Nd doublet by JK∗mIr. Using the measured splitting and mIr ≍ 0.1–0.2μB (ref. 15), we thereby determine JK ≍ 5–10 meV. In turn, the ordered Nd spins induce a much larger effective field on the Ir electrons. This significantly reinforces the order, increases the condensation energy, and enhances the electronic gap, as observed5. To check this proposition, we carried out Hartree–Fock calculations on an effective Kondo lattice model (Supplementary Information). Figure 4 shows results of AIAO staggered magnetization φ and the charge gap Δ. We indeed found the enhancement of the charge gap by the Kondo coupling.

Figure 4: AIAO order and charge gap enhanced by Kondo coupling.
figure 4

AIAO staggered magnetization φ (green) and charge gap Δ (red) as a function of Kondo coupling JK. The results are from a mean-field calculation with U = 0.4, 0.5, 0.6, and 0.7. The unit of energy is given by oxygen-mediated hopping of Ir electrons, toxy (Supplementary Information).

Full size image

We now consider the field-tuned quantum MIT. This occurs for B ≥ 10 T, where M is nearly saturated: this implies the Zeeman term for Nd dominates over JK, and hence the Nd spins are nearly fully polarized along their local z axes: in particular, when the field is at an angle |θ| < 15° from [001] they adopt a 2in–2out configuration, whereas for other angles they take a 3in–1out form. With the Nd spins polarized in the 2in–2out state, the condensation energy from the Kondo term is completely lost, which provides a mechanism to destroy the AF order. Indeed, we found a transition to a metallic or semimetallic state at low field for the [001] orientation, and not at all or at much higher fields along [110] or [111]. For the same model, we also found that the Kondo coupling JK generally stabilizes the zero-field AIAO order even when it is absent for JK = 0 (Fig. 4). The order of the quantum field-tuned transition can be first or second order in the Hartree–Fock approximation, but a first-order behaviour is likely when fluctuations beyond Hartree–Fock are included (Supplementary Information).

Finally, we discuss effects related to domain boundaries. We focus on the low-field part of the anisotropic MR effect in Fig. 2a. Compared to the [001] direction, no marked MIT is seen for B ‖ [111]. Instead, the [111] MR shows complex hysteresis corresponding to changes in the Nd spin structure (Fig. 3c). The results (black line) in the initial up-sweep process after ZFC show a gradual decrease with field and spikes sharply, reaching a minimum value at 3.4 T. In the consecutive field cycles, the resistance exhibits dips at ±3.9 T, where the derivative of M peaks, revealing the close correlations between the MR and magnetization. Notably, the MR after the initial sweep forms a smooth curve interrupted only near the spin-flop transition by a temporary dip.

These observations can be understood in terms of two Ising domains of the AIAO order (Fig. 1a) which can be aligned by a [111] field23. Without such alignment, the initial zero-field state has multi-domains, and hence its lower resistivity may be attributed to more conductive domain walls. This is also consistent with the dip in the spin-flop region of the hysteresis loop, where again domains are generated. Thus the Ising domain walls must be relatively conducting, as recently proposed theoretically24.

It is useful to compare our result to the manganites1,2, which provide a rare example of a field-induced MIT at a comparable field to the one discovered here in Nd2Ir2O7. The two are quite distinct, as the former MIT is strongly first order at all temperatures, whereas in Nd2Ir2O7 the MIT appears continuous in zero field and transforms through a tricritical point to a first-order transition as it is pushed to zero temperature in field. This may be connected to the phenomena of fluctuation-driven first-order transitions in ferromagnetic quantum criticality25, as the AIAO state, like the ferromagnetic state, has a zero-momentum order parameter. Yet Nd2Ir2O7 is unique in that the symmetry breaking and the MIT occur together, and in the prospect to observe topological phenomena in the transition region. Future studies should investigate the Hall effect as a probe of the latter.

Note added in proof: After submitting this manuscript, we became aware of a parallel work by Ueda et al. 26, who observed a similar field-induced MIT. To avoid the influence of the freezing of Nd moments below 15 K on the MIT, a more stoichiometric single crystal with a higher MIT temperature (TMI ∼ 20 K) was used in our study compared to the single crystal (TMI ∼ 15 K) in ref. 26. The higher-quality sample allowed us to find the existence of the possible tricritical points that are missed in the paper by Ueda and colleagues26.

Methods

Sample preparation and characterization.

Several batches of single crystals of Nd2Ir2O7 have been grown by a potassium fluoride flux method27. Powder and single-crystal X-ray diffraction analyses show a single-phase pyrochlore structure with lattice constant a = 10.386(3) Å. The MIT of pyrochlore iridates is known to be very sensitive to the stoichiometry and the transition temperature can be reduced rapidly with doping—as clarified, for example, for Eu2Ir2O7 (ref. 28). Thus, we performed a careful chemical analysis using electron-probe microanalysis (EPMA) and found a slight deviation from stoichiometry in the Ir/Nd ratio of approximately 1% for the single crystals with zero-field TMI ∼ 27 K and of approximately 2% for the single crystals with with zero-field TMI ∼ 20 K.

The magnetotransport was measured by a standard four-probe method with the current path along the [] direction, and the magnetic field was always oriented perpendicular to the current direction. d.c. resistivity measurements in a d.c. magnetic field were carried out using a commercial system (PPMS, Quantum Design) which has a base temperature of 2 K and a maximum magnetic field of 14 T. For the field sweep measurements shown in Fig. 3c, the sample was first cooled down to 2 K under zero field and then the resistivity was measured by sweeping the magnetic field successively from 0 to 14 T, then from 14 to −14 T, and finally from −14 to 14 T. Electrical transport measurements up to 50 T in the pulsed high magnetic field were performed with frequency f = 100 kHz and electrical current I = 280 μA at the International Megagauss Laboratory at ISSP, the University of Tokyo. During the measurements, the electrical current was applied in the [] direction within the (001) plane, as schematically shown in Fig. 2b. The field dependence of the magnetization in a field up to 14 T (Fig. 3a) was measured using a commercial vibrating sample magnetometer system (PPMS, Quantum Design). The temperature dependence of the magnetization shown in Fig. 1c was measured using a commercial SQUID (superconducting quantum interference device) magnetometer (MPMS, Quantum Design) in zero-field cooling (ZFC) and field cooling (FC) procedures from 2 to 300 K.

Spin-model analysis.

We analysed an effective spin model for the Nd moments, including all nearest neighbour interactions allowed by symmetry, Zeeman coupling to the external field, and a staggered Zeeman coupling representing the effect of Ir AIAO order. We studied the magnetization curve by treating the Nd spins as classical vectors and locally minimizing the energy, assuming a q = 0 spin configuration.

Mean-field theory.

The magnetic ground state and electronic structure of the Kondo lattice model were calculated by a self-consistent mean-field method assuming q = 0 magnetic order. The electron–electron correlation was taken into account by the unrestricted Hartree–Fock method, and the localized spins were treated as classical vectors. We adopted a 32 × 32 × 32 superlattice of the four-site unit cell, with periodic boundary conditions for the calculation.