Main

Turbulent fluids are ubiquitous in nature, arising for sufficiently large characteristic speeds U, depending on the kinematic viscosity ν and a characteristic system scale, such as the diameter of a pipe D. Turbulent flows are complex, stochastic, and unpredictable in detail, but transition at lower velocities to a laminar flow, which is simple, deterministic and predictable. This transition is controlled by the dimensionless parameter known as the Reynolds number, which in the pipe geometry of interest here is given by Re ≡ UD/ν, and occurs in the range 1,700 ≲ Re ≲ 2,300. The laminar-turbulence transition has presented a challenge to experiment and theory since Osborne Reynolds’ original observation of intermittent ‘flashes’ of turbulence1.

To explore this transitional regime, we have performed direct numerical simulations of the Navier–Stokes equations in a pipe of length L = 10D, using the open-source code ‘Open Pipe Flow’23, as described in Supplementary Methods. The Reynolds number at which transitional turbulence occurs is higher for short pipes23, and the simulations reported here for L = 10D were performed at a nominal value Re = 2,600, which we estimate to be equivalent to Re ≲ 2,200 in long pipe data7 based on estimates of when puff decay transitions to puff splitting. We confirmed that our results did not qualitatively change for a longer pipe with L = 20D. We denote the time-dependent velocity deviation from the Hagen–Poiseuille flow by u = (uz, uθ, ur). Because we were interested in transitional behaviour, we looked for a decomposition2,6,24,25 of large-scale modes that would indicate some form of collective behaviour, as well as small-scale modes that would be representative of turbulent dynamics. In particular, we report here the behaviour of the velocity field , where the bar denotes average over z and θ, and . We refer to this as the zonal flow. In Fourier space, the zonal flow is given by , where k is the axial wavenumber and m is the azimuthal wavenumber, r is the real space radial coordinate and the tilde denotes Fourier transform in the θ and z directions only. Turbulence was represented by short-wavelength modes, whose energy is .

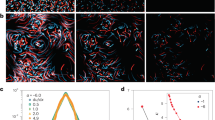
Shown in Fig. 1a is a time series for the energy of the zonal flow, compared with the energy ET(t) of the turbulent energy. The curves show clear persistent oscillatory behaviour, modulated by long-wavelength stochasticity, as shown in the phase portrait of Fig. 1b. In Fig. 1c, we have calculated the phase shift between the turbulence and zonal flows, with the result that the turbulent energy leads the zonal flow energy by ∼π/2. This suggests that these oscillations can be interpreted as a time-series resulting from activator–inhibitor dynamics, such as occurs in a predator–prey ecosystem. Predator–prey ecosystems are characterized by the following behaviour: the ‘prey’ mode activates the ‘predator’ mode, which then grows in abundance. At the same time, the growing predator mode begins to inhibit the prey mode. The inhibition of the prey mode starves the predator mode, and it too becomes inhibited. The inhibition of the predator mode allows the prey mode to re-activate, and the population cycle begins again.

Figure 1: Predator–prey oscillations in transitional turbulent pipe flow at nominal Re = 2,600, for a pipe of radius R = D/2.
figure 1

a, Energy versus time for the zonal flow (orange) and turbulent modes (green). b, Phase portrait of the zonal flow and turbulent modes as a function of time, with colour indicating the earliest time in dark blue progressing to the latest time in light green. c, Phase shift between the turbulent and zonal flow modes as a function of frequency, showing that the turbulence leads the zonal flow by π/2, consistent with predator–prey dynamics. The phase shift and is shifted to be positive, where is the Fourier transform of the correlation function between the turbulence and the zonal flow in a. The red line corresponds to the dominant frequency in the power spectrum. The phase shift near small ω is scatter due to the finite time duration of the time series. d, Velocity field configuration of the zonal flow mode . The colour bar indicates the value of . e, Snapshot of the Reynolds stress gradient and zonal flow time derivative as functions of r. f, Reynolds stress gradient and zonal flow time derivative as functions of time. The agreement shows that zonal flow dynamics is driven by the radial gradient of the Reynolds stress.

Full size image

The flow configuration for the predator mode is shown in Fig. 1d, and consists of a series of azimuthally symmetric modes with direction reversals as a function of radius r. Such banded shear flows are known as zonal flows and are of special significance in plasma physics, astrophysical and geophysical flows, owing to their role in regulating turbulence26. The purely azimuthal component of the zonal flow, denoted by , is spatially uniform in z, and the lack of a radial component means that it is not driven by pressure gradients. Thus, it can exist only as a result of nonlinear interactions with turbulent modes. In this sense, it is a collective mode, one with special significance for transitional turbulence.

The simplest way for such an azimuthal shear flow to couple to turbulent fluctuations is through the Reynolds stress τ: however, a uniform Reynolds stress cannot drive a shear flow, so the first symmetry-allowed possibility is the radial gradient of the Reynolds stress26, as expressed in the Reynolds momentum equation. Thus, to probe the dynamics that govern the emergence of the zonal flow, we have calculated the time-averaged radial gradient of the instantaneous Reynolds stress, τ ≡ uθ′ur′, where , and show in Fig. 1f the 4.5-time-unit-running-mean time series of and the radial gradient ∂rτ. Both quantities have been averaged over 0 ≤ z ≤ L, 0 ≤ θ ≤ 2π and R0 ≤ r < R, where R = D/2, R0 = 0.641R, and the resulting time series are clearly highly correlated. In general, it is the case that zonal flows are driven by statistical anisotropy in turbulence, but are themselves an isotropizing influence on the turbulence through their coupling to the Reynolds stress27,28,29. The fact that turbulence anisotropy activates the zonal flow, and that zonal flow inhibits the turbulence, is responsible for the predator–prey oscillations observed in the numerical simulations.

These numerical results suggest that the large-scale zonal flow and the small-scale turbulence are necessary, and perhaps even sufficient components of an effective coarse-grained description of transitional turbulence in the spirit of Landau theory. Following the usual logic of the modern theory of phase transitions30, we construct the effective theory from symmetry principles alone, as there are no small parameters with which to perform a systematic derivation. If correct, this effective predator–prey theory should undergo spatio-temporal fluctuations whose functional form matches the observations for the lifetime and splitting time of turbulent puffs in a pipe.

The simplest system that corresponds to our direct numerical simulations of the Navier–Stokes equations has three trophic levels: nutrient (E), Prey (B) and Predator (A), which correspond in the fluid system to laminar flow, turbulence and zonal flow respectively. The interactions between individual representatives of these levels are given by the following reactions:

where dA and dB are the death rates of A and B, p is the predation rate, b is the prey birth rate due to consumption of nutrient, 〈ij〉 denotes hopping to nearest neighbour sites, and DA and DB are the nearest-neighbour hopping rate for predator and prey respectively, assumed for simplicity here to be the same value DAB for predator and prey. The ‘mutation’ term (B → A) is symmetry-allowed and has the interesting consequence that the diagram of the predator–prey model matches that of pipe transitional turbulence (Supplementary Methods).

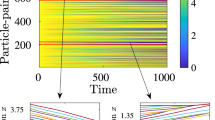
We simulated this predator–prey model, using methods described in Supplementary Methods, in a thin two-dimensional strip on a 401 × 11 lattice. The control parameter is the prey birth rate b. When b is small enough, the population is metastable, and cannot sustain itself, decaying with a finite lifetime τd(b). As b increases, the lifetime of the population increases rapidly: in particular the prey lifetime increases rapidly with b. At large enough values of b, the decay of the initial population is not observed, but instead the initially localized population splits after a time τs(b), spreading outwards and spontaneously splitting into multiple clusters, as shown in the space–time plot of clusters of prey of Fig. 2a.

Figure 2: Stochastic predator–prey model reproduces the phenomenology of transitional pipe turbulence.
figure 2

Lifetime and splitting time of clusters of prey are memoryless processes and obey super-exponential statistics as a function of prey birth rate. To compare with the experiments4, predator–prey dynamics are performed in a two-dimensional pipe geometry as described in the text. a, World line of clusters of prey splitting to form predator–prey travelling waves. The colour measures the local density of prey, corresponding to the intensity of turbulence in pipe flow. In the simulation, the dimensionless parameters are DAB = 0.1, b = 0.1, p = 0.2, dA = 0.01, dB = 0.01 and m = 0.001. In the model simulated, diffusion is isotropic, not biased as would be the case corresponding to a mean flow, where the clusters will accumulate at large times with a well-defined separation set by the depletion zone of nutrient behind each predator–prey travelling wave. b, Log lifetime of prey cluster and splitting time as a function of prey birth rate. The upward curvature signifies super-exponential behaviour. The parameters are DAB = 0.01, p = 0.1, dA = 0.015, dB = 0.025 and m = 0.001. Inset: Double log lifetime versus prey birth rate, showing the fit to the following functional forms: the dashed curve is given by τd/τ0 = exp(exp(46.539b − 0.731)), and the solid curve is given by τs/τ0 = exp(exp(−31.148b − 3.141)).

Full size image

To quantify these observations, we have measured both the lifetime of population clusters in the metastable region and their splitting time using a procedure directly following that of the turbulence experiments and simulations7, and described in Supplementary Methods. We comment that both timescales involve implicitly measurements of quantities that exceed a given threshold, and thus it is natural that the results are found to conform to extreme value statistics12,31.

In Fig. 2a we show the phenomenology of the dynamics of initial clusters of prey, corresponding to the predator–prey analogue for the experiments in pipe flow which followed the dynamics of an initial puff of turbulence injected into the flow4. Depending on the prey birth rate, the cluster decays either homogeneously or by splitting, precisely mimicking the behaviour of turbulent puffs as a function of Reynolds number. The extraction from data of decay times is described in Supplementary Methods. In Fig. 2b is shown the semi-log plot of lifetime for both decay and splitting as a function of prey birth rate, the upward curvature indicative of super-exponential behaviour. The inset to Fig. 2b shows a double exponential plot of puff lifetime and splitting time versus prey birth rate, the straight line being the fit to the functional form indicated in the caption. These figures indicate a remarkable similarity to the corresponding plots obtained for transitional pipe turbulence in both experiments4 and direct numerical simulations7, and demonstrate conclusively that experimental observations are well captured by an effective two-fluid model of pipe flow turbulence with predator–prey interactions between the zonal flow and the small scale turbulence.

Our simulations show that the predator–prey model expressed by equation (1) exhibits a rich phase diagram that captures the main features observed in transitional turbulence in pipes. We can understand the qualitative features of the phase diagram from linear stability analysis of the mean field solution of the predator–prey equations22. Near the transition, the solutions are linearly stable, all eigenvalues are real and there are no spatial-temporal oscillations. But for higher values of b, the eigenvalues develop an imaginary part, a necessary condition for the breakdown of spatially homogeneous prey domains into periodic travelling wave states32. The phase diagram is sketched in Fig. 3, along with the corresponding phase diagram for transitional pipe turbulence as determined by experiment. The phenomenology of the predator–prey system mirrors that of turbulent pipe flow.

Figure 3: Schematic phase diagram for transitional pipe turbulence as a function of Reynolds number compared with the phase diagram for predator–prey dynamics as a function of prey birth rate.
figure 3

For each phase is shown a typical flow or predator–prey configuration, indicating the similarity between the turbulent pipe and ecosystem dynamics.

Full size image

To determine the universality class of the non-equilibrium phase transition from laminar to turbulent flow, we use the two-fluid predator–prey mode in equation (1). Near the transition to prey extinction, the prey population is very small and no predator can survive, and thus equation (1) simplifies to

These equations are exactly those of the reaction-diffusion model for directed percolation33. The argument here is heuristic but the result is correct and can be obtained systematically from statistical field theory techniques, as described in Supplementary Methods.

The observation of the emergence of a zonal flow, excited by the developing turbulent degrees of freedom and the demonstration of its role in determining the phenomenology of transitional pipe turbulence has an interesting consequence: the zonal flow can be assisted by rotating the pipe, and this should catalyse the transition to turbulence, causing it to occur at lower Re. Indeed experiments on axially-rotating pipes34 are consistent with this prediction.

Our work underscores not only the potential importance of zonal flows in other transitional turbulence situations9,10, but also shows the utility of coarse-grained effective models for non-equilibrium phase transitions, even to states as perplexing as fluid turbulence.