Main

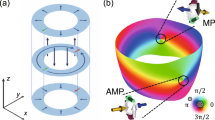
The magnetic domain wall (DW) has received significant attention because of the academic interest it inspires, as well as its potential applications in data storage and logic devices5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24. The dynamics of the DW consists of unique, nonlinear behaviour in response to an external magnetic field. In one-dimensional wires, the DW velocity increases linearly with the external magnetic field up to a threshold, beyond which it abruptly decreases. The abrupt reduction of DW velocity is due to the onset of precessional DW motion, which causes a periodic change in the helicity of the DW (Fig. 1a and Supplementary Fig. 5). This is a well-known phenomenon in field-driven DW dynamics, and is referred to as the Walker breakdown (WB; refs 8,15). An actual DW, however, may have two-dimensional configurations, where the coherent precessional motion of the DW above the threshold field (hereafter the Walker field) should be replaced by the nucleation and propagation of vertical Bloch lines (VBLs; Fig. 1b)8.

Figure 1: Schematic illustration of Walker breakdown (WB) phenomenon.
figure 1

a, Precessional domain wall (DW) motion in a one-dimensional wire. b, Formation of vertical Bloch line (VBL) in a two-dimensional wire. c, Four degenerate VBLs with different charges and chiralities.

Full size image

The VBL, a magnetic curling structure that divides the DW, is considered to be a topological defect as its stability can be determined on the basis of a topological argument. The VBL has four-fold degeneracy that depends on the magnetic charge (Q = ±1) and chirality (C = ±1/2). Here, the topological charge corresponds to the sign of magnetic charge at the centre of the VBL—that is to say, Q = +1 for head-to-head spin alignment and Q = −1 for tail-to-tail spin alignment. Positive (negative) chirality is defined as clockwise (anticlockwise) rotation of the spin. The half-integer feature of the chirality indicates the half-cycle of the spin rotation (so called π-VBL). We define the four degenerate states of VBLs as shown in Fig. 1c. The four degenerate states all generally share the same energy level, and thus appear with equal probability10. Above the Walker field, VBLs are continuously nucleated and are driven out of the sample through the edge (Fig. 1b), resulting in a reduced average DW velocity, which is analogous to the WB phenomenon in a one-dimensional wire.

The velocity breakdown due to the WB generally limits the functional performance in DW-motion-based devices, and thus efforts have been made towards avoiding it. To suppress the WB, several proposals have been suggested on the basis of micromagnetics simulations16,17,18,19,20. In the proposed methods, however, a particular geometry is required to suppress the WB. By way of contrast, here we report on our experimental discovery that the WB can be completely suppressed under the strong Dzyaloshinskii–Moriya interaction (DMI; refs 2,3), which inherently exists at the interface in ferromagnetic/nonmagnetic bilayer structures6,7,21,22,23. Such a suppression of the WB is observed in two-dimensional wires because the evolution of the topological VBL plays a key role in the suppression of the WB, as we will describe later.

For this study, two types of perpendicularly magnetized Co/Ni films were prepared; one is a symmetric Co/Ni with negligible DMI and the other is an asymmetric Co/Ni, which we expect to have a strong DMI owing to the structural inversion asymmetry21,22,23 (see Methods). The Co/Ni films are then patterned into microstrips to investigate the DW dynamics, as shown in Fig. 2a. To measure the DW velocity in a flow regime, we developed a time-of-flight measurement for DW propagation. The details of the sample geometry and the measurement procedure are described in Methods and the Supplementary Information.

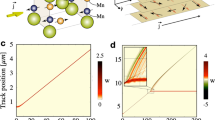
Figure 2: Device structure with measurement set-up and field-driven domain wall (DW) velocity.
figure 2

a, Scanning electron microscope image of the sample in a measurement configuration. Inset shows the schematic illustrations of magnetization states for the signal trace and the reference trace. b,c, DW velocity as a function of the magnetic field H for symmetric (b) and asymmetric (c) Co/Ni wires. Inset in b zooms into the DW velocity for the symmetric Co/Ni wire. Error bars are about the same size as the symbols (red dots). Solid lines in b and c are the calculated DW velocity with various values of D based on the one-dimensional model. Experimentally determined material parameters are used. d,e, Simulated DW velocity with various values of D for symmetric (d) and asymmetric (e) Co/Ni wires. f, Simulated DW velocity for an ideal wire. For all figures, the units of D are mJ m−2.

Full size image

Figure 2b, c shows the DW velocity as a function of |H| for symmetric and asymmetric Co/Ni wires, respectively. A clear threshold field originating from the pinning of wires is observed, implying that the DW velocities measured over the threshold field belong to the flow regime24. We observed a distinct difference in the DW velocity between symmetric and asymmetric Co/Ni wires. The DW velocity of the asymmetric wire is much larger than that of the symmetric wire, and it remains almost constant above 150 mT. On the other hand, the DW velocity in the symmetric wire is comparatively smaller and increases slightly with the magnetic field.

To elucidate the underlying mechanism, we first check the Walker field in our sample on the basis of the one-dimensional DW model, including the interfacial DMI parameter D (ref. 5), which causes a cycloidal magnetization structure. The calculated DW velocities are plotted as solid lines in Fig. 2b, c for various values of D. It is clear that the Walker field is far below the pinning field of our samples, implying that the WB phenomenon is obscured by the DW creep motion that results from pinnings24. This implies that the DW velocities observed in Fig. 2b, c belong to the precessional regime.

Micromagnetics simulations were performed to help understand the experimental results. Two-dimensional wires including a pinning distribution were used for the simulation. The details of the simulation are described in the Methods. Figure 2d, e shows the simulation results of DW velocity for various values of D using the material parameters for symmetric and asymmetric Co/Ni wires, respectively. The simulations reproduce the experimental results fairly well by assuming that D = 0.14 mJ m−2 and D = 0.6 mJ m−2 for symmetric and asymmetric wires, respectively. We performed further simulations in an ideal wire to avoid the complexities that result from the pinnings. Figure 2f shows the DW velocity as a function of the out-of-plane magnetic field for various values of D. In the absence of the DMI (that is, D = 0 mJ m−2), the DW velocity follows the conventional Walker rigid body model, which predicts a velocity breakdown above the Walker field (see the inset of Fig. 2f)15. Interestingly, however, as the DMI increases, such a velocity breakdown is gradually suppressed and the DW velocity maintains its maximum value for a wide range of magnetic fields, even above the Walker field.

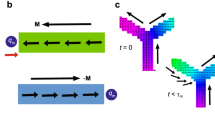
The time evolution of the magnetization distribution of the DW sheds light on the effect of the DMI on the DW motion. Figure 3a, b shows snapshots of a moving DW above the Walker field (|H| = 15 mT for D = 0 mJ m−2 and |H| = 150 mT for D = 1.0 mJ m−2, respectively) (see also Supplementary Movies 1 and 2). It is clearly shown that the VBLs appear inside the DW, indicating the two-dimensional nature of the wire. Noticeably, the dynamics of the VBLs strongly depends on the DMI. For D = 0 mJ m−2, the VBLs nucleated inside the DW propagate to the edge (see Fig. 3c). On the other hand, for the case of D = 1.0 mJ m−2, the VBLs nucleated inside the DW annihilate immediately by emitting spin waves (see Fig. 3d). This intriguing feature can be understood on the basis of the topological features of VBLs.

Figure 3: Snapshots of a moving domain wall (DW).
figure 3

a, Snapshots of a moving DW for D = 0 mJ m−2 with an applied field of |H| = 15 mT. b, Snapshots of a moving DW for D = 1.0 mJ m−2 with an applied field of |H| = 150 mT. The elapsed time between the panes in each figure is 0.2 ns for a and 0.1 ns for b. The applied field pushes the DW towards the right. The colour code for the in-plane magnetization component is shown by a colour wheel. The image height is 500 nm. c,d, Schematic illustrations of the evolution of VBLs for the enclosed regions in a and b, respectively.

Full size image

Figure 4a shows the DW anisotropy energy profile as a function of ϕ. Here, ϕ is the azimuthal angle of the DW defined in the x–y plane, as denoted in Fig. 1b. The DW anisotropy energy (∼cos2ϕ) has two equivalent minima at ϕ = ±π/2 for one cycle of spin rotation (−π < ϕ < π); that is to say, the spin aligned along the +y direction is energetically equivalent to that aligned along the −y direction. Because the spins can rotate in opposite directions with equal probability, the VBL has four degenerate states with different topological charges (Q = ±1) and chiralities (C = ±1/2; refs 8,10,25), as shown in Fig. 1c.

Figure 4: Energy profiles and unidirectional collision of vertical Bloch lines (VBLs).
figure 4

a, Domain wall (DW) anisotropy energy, DMI energy and total energy (from top to bottom) versus the azimuthal angle of the DW. b, Schematic illustration of the evolution of a VBL under D = 0 mJ m−2. The purple arrows indicate the local spin precession. c, Schematic illustration of energy splitting of a degenerate VBL. d, Schematic illustration of unidirectional collision of VBLs under a strong DMI. The purple arrows indicate the locking of the azimuthal angle ϕ that results from the unidirectional collision of VBLs. e, Time evolution of the average azimuthal angle of the DW above the WB. The strength of the DMI D and the magnetic field H are denoted in the legend.

Full size image

The evolution of the VBL (nucleation, propagation and annihilation processes) is governed by topological constraints. During the nucleation or annihilation process, the total topological charge should remain constant—that is, ∑ iQibefore = ∑ iQiafter (refs 26,27). The total chirality (∑ iCi) is referred to as the ‘winding number w’, which counts how many times the spin is wrapped around the circle through the DW. The winding number is also known as a topological number because configurations with different winding numbers cannot be continuously deformed into each other1. Therefore, the winding number also should remain constant during the nucleation and annihilation processes.

Figure 4b shows an example of the evolution of VBLs in the absence of the DMI. Two VBLs with opposite charge and chirality are nucleated simultaneously to satisfy the topological constraints. Because they have equal energy, they propagate along the DW with equal velocity. Note that the propagation direction is determined by the sign of the chirality. Successive nucleation and propagation of VBLs induces a local spin precession (marked by purple arrows), which is analogous to the precessional motion of a DW in a one-dimensional wire.

In the presence of the DMI, however, the topological characteristics of the DW are very different. The DMI energy, unlike the DW anisotropy energy, has cos ϕ symmetry5, which has only one single energy minimum for −π < ϕ < π. A schematic illustration of the energy profile is shown in Fig. 4a. When the DMI energy and DW anisotropy energy coexist, the DMI energy distorts the periodic nature of the DW anisotropy energy and lifts the degeneracy of the VBL, splitting the energy levels into two sub-levels, as shown in Fig. 4c.

Such an energy splitting of the VBL influences the dynamics of the DW considerably. As a result of the energy splitting, the width of the VBL in the two energy levels becomes different. Here, the width of the VBL is defined by , where A is the exchange stiffness constant and Kdeff is an effective DW anisotropy energy including the DMI energy. Considering that the velocity of the VBL is proportional to its width25, the VBLs in the ground state become much faster than those in the excited state. Such a velocity difference induces a unidirectional collision of two VBLs (ref. 28) (see Supplementary Information for a theoretical description). The schematic illustration of unidirectional collision is shown in Fig. 4d. Two VBLs with opposite charge and the same chirality move in the same directions as those in Fig. 4b. (VBLs marked by green and red colours in Fig. 4d). However, owing to the DMI-induced energy splitting, the velocities of the two VBLs are very different, and they finally collide with each other. This is the underlying reason why we did not observe the propagation of VBLs in Fig. 3d. Here, importantly, the unidirectional collision violates the topological constraint in the winding number, because the winding number changes from w = 1 to w = 0 during collision. Hence, the annihilation of the VBL inside the DW is required to release a large amount of energy, which can be achieved through spin wave emissions, as shown in Fig. 3b.

Interestingly, the unidirectional collision of two VBLs suppresses the local spin precession (compare the purple arrows in Fig. 4b and d). This shows an important result: namely, that the continuous annihilation of VBLs induces another constraint on the DW. More specifically, the average azimuthal angle of DW (ϕ) should remain constant even beyond the Walker field. Figure 4e shows the time evolution of ϕ above the Walker field (|H| = 15 mT for D = 0 mJ m−2 (red line) and |H| = 150 mT for D = 1.0 mJ m−2 (blue line)). Here, ϕ is obtained by averaging the angle of the total magnetic moment inside the DW at a given time. Without the DMI, ϕ shows a continuous increase with time, corresponding to the precessional motion of DW. On the other hand, under a strong DMI, the change of ϕ is suppressed and ϕ is fixed around π/2. In Fig. 4e, we also plot ϕ for |H| = 75 mT (green line) just before the Walker field, in which the DW reaches peak velocity without precession (see Supplementary Movie 3). The results show that the average angle ϕ is almost the same for |H| = 75 mT and 150 mT. This explains why the DW velocity remains constant at a peak velocity under a strong DMI (Fig. 2f). In other words, despite the apparently dissimilar appearance of DWs for |H| = 75 mT and for above the Walker field, they all exhibit the same average angle ϕ, which yields the same velocity. This line of thought is analogous to that regarding the magnetic soliton, in which the DW velocity is determined simply by the azimuthal angle of the DW (ref. 1). So far, such a soliton approach has been applied only in a one-dimensional steady motion of DW before the WB. Interestingly, however, here we find that the soliton-like DW velocity can be extended even above the Walker field in two-dimensional DW configurations under a strong DMI.

The suppression of the WB can be supported by energy considerations in the system. The saturation in the DW velocity above the Walker field (Fig. 2f) implies that another energy dissipation channel is opened, because the dissipation via Gilbert damping (α) cannot follow the Zeeman energy relaxation rate for such a fast DW motion for a high-field regime16,29. We ascribe the additional energy relaxation channel to the local spin wave emission induced by the unidirectional collision of VBLs, because the annihilation of topologically protected defects generally accompanies a large energy relaxation1. Such a spin wave emission can balance with the Zeeman energy relaxation rate for fast DW motion29,30. We confirm this using micromagnetic simulations with α = 0. Even for α = 0, the DW is found to move in two-dimensional wires through the energy dissipation into a new channel—that is, emitting spin waves (see Supplementary Movie 4). Note that we do not observe any DW motion in one-dimensional wires for α = 0, even under a strong DMI. This highlights the fact that the evolution of the VBL is crucial for the DW motion under the DMI. The constant DW velocity across a wide range of out-of-plane fields can be interpreted as meaning that the number of VBLs increases with the field to compensate for the increasing Zeeman energy relaxation rate. An increase in the number of VBLs is indeed observed in our simulation.

Methods

Film preparation and device fabrication.

For this study, two types of perpendicularly magnetized Co/Ni films—that is, symmetric and asymmetric layers—were prepared. For the symmetric Co/Ni sample, we used Si/Ta (4 nm)/Pt (2 nm)/Co (0.3 nm)/Ni (0.6 nm)/Co (0.3 nm)/Pt (2 nm)/Ta (4 nm), for which the interfacial DMI should be cancelled out owing to the structural inversion symmetry. On the other hand, Si/Ta (4 nm)/Pt (2 nm)/Co (0.3 nm)/Ni (0.6 nm)/Co (0.3 nm)/MgO (1 nm)/Pt (2 nm)/Ta (4 nm) was used for the asymmetric Co/Ni sample, with MgO being inserted between the upper Co and Pt layers to break the structural inversion symmetry; accordingly, the interfacial DMI should exist in the asymmetric Co/Ni layer. High-quality Co/Ni films were obtained by using a deposition rate of 0.73 Å s−1 through adjustments to the Ar sputtering pressure (2.7 mPa) and sputtering power (300 W). Wires of width 1 μm and length 50 μm are fabricated by electron beam lithography and Ar ion milling, as shown in Fig. 2a. A 100-nm-wide Hall cross structure was designed to detect DW motion through the anomalous Hall voltage VH. A negative tone electron beam resist (maN-2403) was used for lithography at a fine resolution (∼5 nm). For current injection, two Au (100 nm)/Ta (5 nm) contact lines, labelled A and B, were attached on each nanowire, as shown in Fig. 2a. To make an Ohmic contact, the surface of the nanowire was cleaned by weak ion milling before electrode deposition.

Experimental set-up.

The configuration of the circuit employed is illustrated in Fig. 2a. A pulse generator (Picosecond 10, 300B) was used to generate a current pulse to create the DW. The current pulse propagates through contact line A and is recorded in the oscilloscope (Textronix 7354). The voltage signal originating from the Hall cross is also recorded in the oscilloscope through the 46 dB differential amplifier. The simultaneous recording of the two signals (that is, the current pulse for creating the DW and the Hall voltage for detecting the DW) allowed us to measure the DW arrival time, which can be converted into the DW velocity. A direct current source (Yokogawa 7651, max 30 V, 100 mA) was used to inject direct current to generate the anomalous Hall voltage. The details of the measurement procedure are described in the Supplementary Information.

Micromagnetics simulations.

All micromagnetics simulations were performed using a program developed previously16. A 500-nm-wide wire was used for the simulation. The sample was divided into identical rectangular prisms (cells), in which the magnetization was assumed to be constant. The cross-sectional dimensions of the wire in the simulation were 500 × 1.2 nm2. The moving calculation region, always centred on the DW, was limited to a length of 1 μm along the wire. The exchange field was evaluated from the four neighbouring cells. The demagnetizing field was averaged over the entire cell, and was evaluated using the fast Fourier transform technique, with zero padding to improve the calculation speed. Furthermore, the anisotropy distribution was taken into account in the simulation to reproduce the DW pinning field. The DMI energy originating from the antisymmetric exchange interaction was included together with the other micromagnetic energies, yielding a cycloidal magnetization structure. A boundary condition that took into account the bending of the magnetization at the edges that resulted from the DMI was used. The two-dimensional calculations were performed by dividing the wire into rectangular prisms of size 2 × 2 × 1.2 nm3. The time step was 0.25 ps. The DW velocity was determined over the course of 16 simulations for each magnetic field. For the simulation, we used material parameters as follows: saturation magnetization (MS) and perpendicular magnetic anisotropy (KU) were experimentally determined as MS = 8.37 × 105 A m−1, KU = 0.9 × 106 J m−3 (for symmetric Co/Ni) and KU = 1.31 × 106 J m−3 (for asymmetric Co/Ni). The exchange stiffness was assumed to be A = 1.0 × 10−11 J m−1. The damping constant was set to be α = 0.15, which was approximated from the thickness dependence of a similar Co/Ni film31.