Abstract
Wheeler’s ‘spacetime-foam’1 picture of quantum gravity (QG) suggests spacetime fuzziness (fluctuations leading to non-deterministic effects) at distances comparable to the Planck length, LPl ≈ 1.62 × 10−33 cm, the inverse (in natural units) of the Planck energy, EPl ≈ 1.22 × 1019 GeV. The resulting non-deterministic motion of photons on the Planck scale is expected to produce energy-dependent stochastic fluctuations in their speed. Such a stochastic deviation from the well-measured speed of light at low photon energies, c, should be contrasted with the possibility of an energy-dependent systematic, deterministic deviation. Such a systematic deviation, on which observations by the Fermi satellite set Planck-scale limits for linear energy dependence2, is more easily searched for than stochastic deviations. Here, for the first time, we place Planck-scale limits on the more generic spacetime-foam prediction of energy-dependent fuzziness in the speed of photons. Using high-energy observations from the Fermi Large Area Telescope (LAT) of gamma-ray burst GRB090510, we test a model in which photon speeds are distributed normally around c with a standard deviation proportional to the photon energy. We constrain the model’s characteristic energy scale beyond the Planck scale at >2.8EPl(>1.6EPl), at 95% (99%) confidence. Our results set a benchmark constraint to be reckoned with by any QG model that features spacetime quantization.
Similar content being viewed by others
Main
Significant advances in exploring QG-motivated phenomenology3 have been achieved in the past decade. In some cases, it was possible to establish bounds on QG effects at the Planck scale. Among the possible QG effects, it is expected4,5,6 that the postulated foamy/fuzzy structure of spacetime at short distances would induce a stochastic effect, where two massless particles of equal energy travel the exact same distance in different times. In this work, we examine a model of spacetime foam6, in which quantum fluctuations of spacetime near the Planck scale induce stochastic variations in the speed of light, v(E) = c + δv(E), where δv(E) is random and distributed normally around zero with a standard deviation  In this model, we observationally expect a bunch of photons of equal energy E emitted simultaneously from a distant astrophysical source to propagate with different speeds and arrive at different times, normally distributed around the light travel time T for v(E) = c, with a standard deviation σT(E) = Tcσv(E)/c, where Tc ∼ T is given by7:
In this model, we observationally expect a bunch of photons of equal energy E emitted simultaneously from a distant astrophysical source to propagate with different speeds and arrive at different times, normally distributed around the light travel time T for v(E) = c, with a standard deviation σT(E) = Tcσv(E)/c, where Tc ∼ T is given by7:

with H0 = 100h km s−1 Mpc−1 being the Hubble constant and [ΩΛ, ΩM, h] = [0.73,0.27,0.71] the cosmological parameters we used.
This stochastic speed-of-light variation is in conflict with Lorentz invariance, the basic symmetry of Einstein’s theory of relativity. Such a conflict is usually referred to as Lorentz invariance violation (LIV). Here, we examine a simple manifestation of ‘stochastic LIV’, in which the light-cone of special relativity still exists; however it is fuzzy. The dimensionless parameter determines the energy scale EPl of stochastic LIV, and the model-dependent parameter ns determines the leading-order energy dependence of the effect. Stochastic LIV should be distinguished from deterministic LIV, for which LIV-induced dispersion is exactly the same for all photons of the same energy E (that is, it is systematic) and is given by  with = ±1 a model-dependent parameter.
with = ±1 a model-dependent parameter.
Systematic LIV represents a more appreciable departure from the structure of present theories, as in it the special-relativistic light-cone does not merely acquire some fuzziness but is actually replaced by a new structure. Moreover, whereas one should expect all spacetime-foam models to inevitably produce some amount of light-cone fuzziness of the type that induces stochastic LIV, systematic LIV requires spacetime foam with very particular properties.
It follows immediately from Wheeler’s picture of spacetime foam1 that for a particle of energy E propagating in the foam, the travel time T from source to detector should be uncertain following a law that could depend only on the distance travelled, the particle’s energy and the Planck scale, with leading-order form of the type δT ∼ xnEm/EPl1+m−n, where m and n are model-dependent powers and 1 + m − n > 0. QG phenomenology is at present focused mostly on effects suppressed at the (first power of the) Plank scale, as stronger suppression leads to even weaker effects4. Therefore, we focus on cases with n = m. The particular case n = m = 0 is a rather natural option, which, however, cannot be tested, as it requires timing with Planck-time (tPl ≈ 5.39 × 10−44 s) accuracy. As will become clear shortly, the picture we focus on here corresponds to the next natural choice of n = m = 1, that is, δT ∼ xE/EPl.
Even though the model of spacetime-foam effects examined here is rather natural, its applicability to specific QG theories is in most cases difficult to establish, as obtaining rigorous physical predictions within the various complex QG mathematical formalisms is typically challenging. However, this model does apply to the important class of QG formalisms based on the so-called ‘Lie-algebra non-commutative spacetimes’8,9, which feature non-commutativity of coordinates of type  This class of QG formalisms plays a key role in the only QG theory that has been solved so far—the dimensionally reduced 2 + 1D version of QG. Moreover, research on 3 + 1D QG has increasingly focused on Lie-algebra non-commutative spacetimes, for which the phenomenology examined here also applies.
This class of QG formalisms plays a key role in the only QG theory that has been solved so far—the dimensionally reduced 2 + 1D version of QG. Moreover, research on 3 + 1D QG has increasingly focused on Lie-algebra non-commutative spacetimes, for which the phenomenology examined here also applies.
To test the hypothesis of stochastic speed-of-light variations, we need bursts of photons of high energy and short duration observed from very distant sources. Gamma-ray bursts (GRBs) are ideal sources for this task10, thanks to their large distances (up to redshift11 z ∼ 9.4), rapidly varying emission (minimum variability timescale down to ms), and high-energy extent of their emission (up to tens of GeV).
GRB090510 occurred at cosmological redshift12 z = 0.903 ± 0.001 and was one of the brightest GRBs ever detected13. It was an exceptional GRB with a short duration (∼1 s), a very high luminosity, photons of very high energy (up to ∼31 GeV), and a fine temporal structure with ∼10 ms spikes in its light curve13,14. The best and most robust limits for both nd = 1 and nd = 2 deterministic LIV were obtained using observations of this burst2,15. Here, we use photon arrival time and energy data produced by the Fermi LAT (ref. 16) observations of GRB090510 to place a stringent constraint on ξs, 1. We consider only ns = 1, because for ns = 2 the limits are several orders of magnitude away from the Planck scale, and thus not constraining QG models in a physically meaningful degree.
We adopt and modify for the case of stochastic effects a well-established maximum-likelihood analysis that was successfully used to search for deterministic LIV-induced energy dispersion in active galactic nuclei15,17,18 and GRBs (ref. 15; see Supplementary Information). We start the analysis by assuming that, without stochastic LIV, the detected GRB light curve would be identical across the whole observed Fermi-LAT energy range (from ∼10 MeV to tens of GeV). We then split the data into two energy ranges, separated by a threshold energy Eth. The photons below Eth are used to estimate how the GRB emission’s time profile would have been detected on average without LIV (the ‘light curve template’, f(t)), whereas the photons above Eth are used for evaluating the likelihood function. The threshold energy Eth is chosen to be low enough such that any dispersion effects below it are effectively negligible, yet high enough to allow adequate statistics for accurately estimating the light curve template. Based on simulations using synthetic data sets inspired by GRB090510, we chose Eth = 300 MeV; a choice that corresponds to increased sensitivity and minimal systematic biases.
We focus on the brightest, most variable time interval possessing the highest-energy photons of the GRB’s prompt emission. To minimize systematic biases, we then analyse a sub-interval of it, during which the GRB energy spectrum was measured to be relatively stable13, namely 0.7–1.0 s post-trigger. Our chosen time interval and Eth correspond to 316 photons below Eth and 37 photons above Eth.
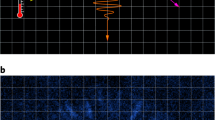
Guided by simulations, we estimate the light curve template using a 6-ms bandwidth kernel-density estimate of the detected emission below Eth. Figure 1 shows the estimated light curve template along with histograms of the arrival times of photons with energies below and above Eth. Using a maximum-likelihood analysis, we search for any dispersion in the high-energy part of the data (above Eth) that is in excess of that below Eth. Assuming no source-intrinsic effects, we interpret any excess dispersion at high energies as arising from spacetime-foam effects, and use its presence or lack thereof to constrain these effects. For the examined case of ns = 1, we quantify the magnitude of LIV-induced dispersion using the quantity w(z) = σT(E)/E. According to our maximum-likelihood analysis, the best estimate for w is wbest = 0 s GeV−1. This null result corresponds to the complete absence of any measurable excess dispersion in the high-energy part of the data.
To produce a confidence interval on w we employ the Feldman–Cousins (FC) approach19, as it provides confidence intervals of proper coverage and is also less sensitive to biases in the estimation of wbest. The implementation of the FC approach involved a set of simulations in which we first injected data sets similar to that of GRB090510 with various degrees of stochastic dispersion (w), and then applied the maximum-likelihood analysis to measure this dispersion (that is, derive wbest). By examining the distribution of measured dispersion values (wbest) for each particular value of the injected dispersion (w), we found which values of true dispersion are possible given our measurement of wbest = 0 s GeV−1, thereby producing a confidence interval on w. Figure 2 shows the results of these simulations along with the resulting FC confidence belt, which we used to place the constraints of wbest < 0.013 (0.023) s GeV−1 at 95% (99%) confidence. These constraints on w for the redshift of GRB090510, z = 0.903, correspond to constraints of ξs, 1 > 2.8 (1.6) at 95% (99%) confidence, respectively. These are the first-ever constraints on spacetime-foam-induced stochastic variations on the speed of light that are beyond the physically important milestone of the Planck scale.
Probability of obtaining a particular value of wbest (x-axis) versus the simulated value of w (y-axis). The pair of red curves shows the 95% Feldman–Cousins confidence belt. The horizontal solid black line denotes our 95% upper limit on w, given the value wbest = 0 s GeV−1 obtained using the actual data. The diagonal thin solid black line denotes the line of equality between the simulated value (w) and the best estimate for this value (wbest).
We extensively tested the validity and robustness of our results (see Supplementary Information). Specifically, we considered how the choice of time interval, the statistical uncertainty in the determination of the light curve template, the presence of spectral evolution, the imperfect energy reconstruction, the uncertainty of the cosmological parameters, and our choice of Eth affect the results. All the effects we examined had little influence on our results, shifting our upper limits by less than 10% (or 20% at worst, for a smaller time interval, 0.8–1.0 s post-trigger), and often by much less, supporting the robustness of our results.
GRBs will probably remain the most constraining sources for direct searches of stochastic speed-of-light variations. Of course, one might alternatively seek indirect evidence of such variations: for example, based on the effect of these variations on the fuzziness of distance measurements operatively defined in terms of photon travel times, L ≡ vT. In this case, contributions to the uncertainty δL ≃ cδT + Tδv in L would include in addition to the standard contribution from the Heisenberg uncertainty principle for a relativistic probe, δT ≥ ℏ/2E = (LPl/2c)EPl/E (where ℏ is the reduced Planck constant), a novel contribution due to the stochastic QG effects:

Equation (1) describes a fuzzy spacetime as there is no value of the energy of the probe for which the distance determination is classically sharp  Minimization with respect to E implies (up to numerical factors of order unity),
Minimization with respect to E implies (up to numerical factors of order unity),  Satisfactorily, this falls within the general expectations for the form of distance fuzziness
Satisfactorily, this falls within the general expectations for the form of distance fuzziness  discussed in previous works4,5,20,21.
discussed in previous works4,5,20,21.
Equation (1) bridges two areas of investigation in quantum gravity: one on stochastic speed-of-light variations and one on a minimum-uncertainty principle for distance measurements. For purposes of exploiting this to perform indirect tests for stochastic speed-of-light variations, one should take notice that the best method to date for testing distance fuzziness relies on its implications on the formation of halo structures in the images of distant quasars5. However, the outcome of those studies depends rather crucially5 on the particular form of the fluctuations of the light-cone in the direction transverse to the one of propagation, in the same sense that our stochastic speed-of-light variations could be modelled purely in terms of fluctuations of the light-cone along the direction of propagation. Any attempt to test stochastic speed-of-light variations on the basis of such quasar-image studies would only produce ‘conditional limits’, affected by assumptions about the fluctuations of the light-cone in the direction orthogonal to the propagation. A very exciting prospect for the future is to combine the type of study of stochastic speed-of-light variations proposed here and the studies of distance fuzziness developed in refs 5, 20, 21 to possibly obtain complementary views (or constraints) on light-cone fluctuations, both in the direction of motion and also in the transverse direction.
Remarkably, in spite of the stochastic nature of the examined dispersion, it was possible to obtain limits that are beyond the Planck scale, and comparable to those obtained for deterministic LIV (refs 2, 15). These stringent limits should be taken into account when considering any QG theory that involves spacetime quantization. Using the methodology presented here, Fermi-LAT observations of GRBs brighter than GRB090510, and future high-sensitivity and higher-energy Cherenkov Telescope Array22,23 observations of short-duration GRBs would enable us to reduce even further the allowed windows for QG models.
References
Wheeler, J. in Relativity, Groups and Topology (eds DeWitt, C. M. & DeWitt, B. S.) 467–500 (Gordon and Breach, 1964).
Abdo, A. A. et al. A limit on the variation of the speed of light arising from quantum gravity effects. Nature 462, 331–334 (2009).
Amelino-Camelia, G. Quantum-spacetime phenomenology. Living Rev. Relativ. 16, 5 (2013).
Amelino-Camelia, G. Gravity-wave interferometers as quantum-gravity detectors. Nature 398, 216–218 (1999).
Christiansen, W., Ng, Y. J. & van Dam, H. Probing spacetime foam with extragalactic sources. Phys. Rev. Lett. 96, 051301 (2006).
Amelino-Camelia, G. & Smolin, L. Prospects for constraining quantum gravity dispersion with near term observations. Phys. Rev. D 80, 084017 (2009).
Jacob, U. & Piran, T. Lorentz-violation-induced arrival delays of cosmological particles. J. Cosmol. Astropart. Phys. 01, 031 (2008).
Majid, S. & Ruegg, H. Bicrossproduct structure of κ-Poincare group and non-commutative geometry. Phys. Lett. B 334, 348–354 (1994).
Madore, J., Schraml, S., Schupp, P. & Wess, J. Gauge theory on noncommutative spaces. Eur. Phys. J. C16, 161–167 (2000).
Amelino-Camelia, G., Ellis, J., Mavromatos, N. E., Nanopoulos, D. V. & Sarker, S. Tests of quantum gravity from observations of γ-ray bursts. Nature 393, 763–765 (1998).
Cucchiara, A. et al. A photometric redshift of z ∼ 9.4 for GRB 090429B. Astrophys. J. 736, 7 (2011).
McBreen, S. et al. Optical and near-infrared follow-up observations of four Fermi/LAT GRBs: redshifts, afterglows, energetics, and host galaxies. Astron. Astrophys. 516, A71 (2010).
Ackermann, M. et al. Fermi observations of GRB 090510: A short-hard gamma-ray burst with an additional, hard power-law component from 10 keV to GeV energies. Astrophys. J. 716, 1178–1190 (2010).
Ackermann, M. et al. The first Fermi-LAT gamma-ray burst catalog. Astrophys. J. Suppl. Ser. 209, 11 (2013).
Vasileiou, V. et al. Constraints on Lorentz invariance violation from Fermi-Large Area Telescope observations of gamma-ray bursts. Phys. Rev. D 87, 122001 (2013).
Atwood, W. B. et al. The large area telescope on the Fermi gamma-ray space telescope mission. Astrophys. J. 697, 1071–1102 (2009).
Martınez, M. & Errando, M. A new approach to study energy-dependent arrival delays on photons from astrophysical sources. Astropart. Phys. 31, 226–232 (2009).
Abramowski, A. et al. Search for Lorentz Invariance breaking with a likelihood fit of the PKS 2155-304 flare data taken on MJD 53944. Astropart. Phys. 34, 738–747 (2011).
Feldman, G. J. & Cousins, R. D. Unified approach to the classical statistical analysis of small signals. Phys. Rev. D 57, 3873–3889 (1998).
Lieu, R. & Hillman, L. W. The phase coherence of light from extragalactic sources: Direct evidence against first-order Planck-scale fluctuations in time and space. Astrophys. J. 585, L77–L80 (2003).
Tamburini, F., Cuofano, C., Della Valle, M. & Gilmozzi, R. No quantum gravity signature from the farthest quasars. Astron. Astrophys. 533, A71 (2011).
Actis, M. et al. Design concepts for the Cherenkov Telescope Array CTA: An advanced facility for ground-based high-energy gamma-ray astronomy. Exp. Astron. 32, 193–316 (2011).
Inoue, S. et al. Gamma-ray burst science in the era of the Cherenkov Telescope Array. Astropart. Phys. 43, 252–275 (2013).
Acknowledgements
The Fermi-LAT Collaboration acknowledges support for LAT development, operation and data analysis from NASA and DOE (United States), CEA/Irfu and IN2P3/CNRS (France), ASI and INFN (Italy), MEXT, KEK and JAXA (Japan), and the K. A. Wallenberg Foundation, the Swedish Research Council and the National Space Board (Sweden). Science analysis support in the operations phase from INAF (Italy) and CNES (France) is also gratefully acknowledged. This research was supported by an ERC advanced grant (GRBs), by the I-CORE (grant No 1829/12), by the joint ISF-NSFC program (T.P.) and by the Templeton Foundation (G.A-C.).
Author information
Authors and Affiliations
Contributions
All authors have contributed significantly to this work. V.V. and J.G. have focused mainly on the data analysis and deriving the limits, whereas T.P. and G.A-C. have focused mainly on the theory parts.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Information (PDF 2116 kb)
Rights and permissions
About this article
Cite this article
Vasileiou, V., Granot, J., Piran, T. et al. A Planck-scale limit on spacetime fuzziness and stochastic Lorentz invariance violation. Nature Phys 11, 344–346 (2015). https://doi.org/10.1038/nphys3270
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys3270
This article is cited by
-
Quantum gravitational decoherence from fluctuating minimal length and deformation parameter at the Planck scale
Nature Communications (2021)
-
Single extra dimension from κ-Poincaré and gauge invariance
Journal of High Energy Physics (2021)
-
The variation of photon speed with photon frequency in quantum gravity
Indian Journal of Physics (2018)
-
Spacetime fuzziness in focus
Nature Physics (2015)