Abstract
A monolayer of a transition metal dichalcogenide such as WSe2 is a two-dimensional direct-bandgap valley-semiconductor1,2 having an effective honeycomb lattice structure with broken inversion symmetry. The inequivalent valleys in the Brillouin zone could be selectively addressed using circularly polarized light fields3,4,5, suggesting the possibility for magneto-optical measurement and manipulation of the valley pseudospin degree of freedom 6,7,8. Here we report such experiments that demonstrate the valley Zeeman effect—strongly anisotropic lifting of the degeneracy of the valley pseudospin degree of freedom using an external magnetic field. The valley-splitting measured using the exciton transition deviates appreciably from values calculated using a three-band tight-binding model9 for an independent electron–hole pair at ±K valleys. We show, on the other hand, that a theoretical model taking into account the strongly bound nature of the exciton yields an excellent agreement with the experimentally observed splitting. In contrast to the exciton, the trion transition exhibits an unexpectedly large valley Zeeman effect that cannot be understood within the same framework, hinting at a different contribution to the trion magnetic moment. Our results raise the possibility of controlling the valley degree of freedom using magnetic fields in monolayer transition metal dichalcogenides or observing topological states of photons strongly coupled to elementary optical excitations in a microcavity10.
Similar content being viewed by others
Main
Charge carriers in two-dimensional (2D) layered materials with a honeycomb lattice, such as graphene and transition metal dichalcogenides (TMDs), have a twofold valley degree of freedom labelled by ±K-points of the Brillouin zone, which are related to each other by time-reversal symmetry7. In TMDs, the low-energy physics takes place in the vicinity of ±K-points of the conduction and valence bands with Bloch states that are formed primarily from and , dxy orbitals of the transition metal, respectively9. The magnetic moment of charged particles in a monolayer TMD arises from two distinct contributions: the intracellular component stems from the hybridization of the and dxy orbitals as ± idxy, which provide the Bloch electrons at ±K in the valence band an azimuthal angular momentum along z of lz = ±2ℏ (Fig. 1a). The second—intercellular—contribution originates from the phase winding of the Bloch functions at ±K-points11,12,13,14. This latter contribution to orbital magnetic moment is different for conduction and valence bands owing to breakdown of electron–hole symmetry. Both contributions yield magnetic-field-induced splitting with an opposite sign in the two valleys.
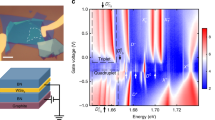
a, A schematic of the band structure showing the valley-dependent intracellular circulation of the valence band electrons. The double circulating clockwise (anticlockwise) arrow denotes the out-of-plane orbital magnetic moment of +2μB (−2μB) arising from d + id (d − id) orbitals in the valence band of the K (−K) valley. The conduction band formed out of the orbital carries no such magnetic moment. b, Typical photoluminescence (PL) spectra at 4.2 K showing the neutral exciton (X0) and negatively charged exciton or trion (X−) resonance at around 708 nm and 722 nm, respectively. The laser polarization is linear and the PL is detected co-polarized (orange) or cross-polarized (purple) to it, showing linear dichroism only for the X0 peak. Solid lines are multi-peak Lorentzian fits to the spectra together with a weak cubic polynomial capturing any non-uniform background.
In a 2D material such as a monolayer TMD, the current circulation from the orbitals can only be within the plane; as a consequence, the corresponding orbital magnetic moment can only point out-of-plane. A magnetic field (B) along z distinguishes the sense of circulation in 2D, causing opposite energy shifts (−μ ⋅ B) in ±K valleys as a result of opposite magnetic moments. The lifting of degeneracy between the two valleys in the presence of B represents a valley analogue of the spin-Zeeman effect. Optical absorption or emission experiments would allow a direct determination of this valley Zeeman effect as the valley index (±K) for independent electron–hole pairs is linked to the helicity of light (σ±) emitted normal to the monolayer3,4,5. On the other hand, it is well known that the optical excitation spectra of TMDs are strongly modified by Coulomb interactions, leading to strongly bound neutral and charged exciton (trion) resonances with non-hydrogenic excited states15,16,17,18,19,20. Moreover, it has been recently shown that the electron–hole exchange interaction couples the ±K valleys21. It is therefore not a priori clear to what extent predictions about circular dichroism or orbital magnetic moments that are based on a non-interacting particle picture remain valid in optical measurements probing exciton or trion resonances.
We perform polarization-resolved photoluminescence (PL) spectroscopy on monolayer WSe2 to identify the low-energy optical excitations (Methods). Figure 1b shows a typical polarization-resolved PL spectrum at zero field. A sizeable ‘valley coherence’ or linear dichroism (∼20%) of the exciton peak (X0) at ∼708 nm confirms its monolayer nature22. The peak at around 722 nm is identified as originating from trion (X−) emission, consistent with the previous PL studies on WSe2 (ref. 22). Polarization-resolved PL measurements yielded a valley-contrasting circular dichroism of less than 20% for both X0 and X− resonances in all the flakes that were measured. As we argue below, the electron–hole exchange-induced mixing of the two valleys is possibly responsible for reducing the degree of circular dichroism21,23.
Figure 2a shows the behaviour of X0 at various B up to 8.4 T in the Faraday geometry (B ∥ z). The PL is analysed in a circularly polarized basis while the excitation of the laser is kept linearly polarized, detuned by over 200 meV from the X0 resonance. A clear splitting of the X0 peak as a function of B is observed: the splitting increases linearly with B, with a slope of about 0.25 meV T−1 (Fig. 2b). The magnitudes of B-dependent splitting in five different flakes are observed to be within ±10% of this value. We have also carried out resonant reflection measurements which showed a similar splitting for the exciton peak (Fig. 2c). The fact that we do not observe the trion peak in reflection measurements indicates that our sample has a low doping density.
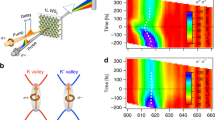
a, Normalized polarization-resolved photoluminescence (PL) spectra of the neutral exciton (X0) peak as a function of the out-of-plane magnetic field (B). The excitation laser is polarized linearly; the red and blue traces correspond to PL analysed in a circularly polarized basis. The spectra at different B are normalized to the zero-field data whereas the spectra at the same B are not normalized. The solid lines are fits to the data. The B-dependent splitting results from the valley Zeeman effect, as depicted in d. b, Splitting extracted from fits in a showing a linear increase with B. The dashed line is a linear fit to the data. c, Resonant differential reflectance spectra at +8.4 T obtained using a white-light source. Solid black lines are fits to the data using an admixture of absorptive and dispersive lineshapes. d, Valley Zeeman effect—in a finite out-of-plane B, the degeneracy between the ±K valleys is lifted as a result of contributions from the spin-Zeeman effect (ΔEs), the intercellular orbital magnetic moment (ΔEinter), and the intracellular contribution from the d ± id orbitals of the valence band (ΔEintra). The signs of these contributions are opposite in the two valleys. ΔEs causes equal energy shifts of the conduction and valence bands, and hence can not be detected in PL. The resulting valley-split transitions are circularly polarized.
The measurement of the magnetic-field dependence of PL in the Voigt geometry (B ⊥ z) shows no observable splitting up to the highest B (Fig. 3a). This extreme anisotropy in the magnetic response of the monolayer is a direct consequence of the fact that the orbital magnetic moment of a strictly 2D material points out-of-plane and thus can couple only to Bz. Our experimental observations also rule out a spin-Zeeman contribution to the measured splitting. In fact, the strong spin–orbit interaction in both the conduction and valence band of WSe2 (refs 24, 25) ensures that the spin degree of freedom is frozen out and does not contribute to the B-induced splitting, which is consistent with earlier studies that reported insensitivity of circular dichroism to an in-plane magnetic field4,26.
a, Exciton photoluminescence spectra as a function of in-plane magnetic field B (Voigt geometry), showing no observable splitting even at the highest applied field of 8.4 T. The dashed vertical line indicates the emission centre wavelength, which is identical for 0 T and 8.4 T. b, Polarity reversal of B leads to switching of the emission helicity of the two peaks together with a sign change of the splitting, consistent with the valley Zeeman effect depicted in Fig. 2d. c, Polarization dependence of magnetic splitting at 8.4 T, showing no clear splitting when the photoluminescence is analysed in the linear basis, confirming that the split peaks are circularly polarized. d, Circular dichroism as a function of out-of-plane magnetic field shows a clear increase by an approximate factor of two. The out-of-plane B can overcome the valley-mixing due to electron–hole exchange interactions, leading to the observed increase.
As expected, if the direction of B in the Faraday geometry is reversed, the helicity of the split peaks also switches (Fig. 3b). When the B-dependent PL data is analysed in a linear basis no clearly resolvable splitting is observed (Fig. 3c); this is a consequence of the fact that the split X0 lines are circularly polarized and have a linewidth that is larger than the maximum attainable B-field-induced splitting. By varying the polarization setting of both the excitation laser and the detection, it is confirmed that the split peaks are of opposite circular polarization, irrespective of the polarization of the excitation laser.
The lifting of the degeneracy of the exciton emission in the circularly polarized basis occurs owing to the equal magnitude but opposite sign of the orbital magnetic moment of the two valleys, together with unequal orbital magnetic moments of conduction and valence band states within the same valley, as shown in Fig. 2d27,28,29,30. For independent electron–hole pair excitations with a vanishing in-plane momentum, the optical transition in each valley experiences a shift in energy which is linear in B, given by  are the sum of the intra- and intercellular orbital magnetic moments of the valence (conduction) bands in the two valleys. Clearly, a necessary requirement for observing splitting in optical transitions is electron–hole symmetry breaking.
are the sum of the intra- and intercellular orbital magnetic moments of the valence (conduction) bands in the two valleys. Clearly, a necessary requirement for observing splitting in optical transitions is electron–hole symmetry breaking.
The magnitude of the intracellular orbital magnetic moment of the valence band in the two valleys is μv = (e/2m)lz = 2μB, where μB = eℏ/2me is the Bohr magneton. With this, one can estimate the magnitude of the splitting arising purely from the magnetic moment of the d-orbitals or the intracellular contribution as  To calculate the intercellular orbital magnetic moment for the two bands, we use the third-nearest neighbour three-band tight-binding parameters for WSe2 (ref. 9), which reproduces the first-principles calculation for the conduction and valence bands in the entire Brillouin zone. As discussed earlier, the optical emission and absorption in TMDs near the band edge have been shown to stem from strongly bound excitons with a Bohr radius (aB) of the order of 1 nm (ref. 18). In reciprocal space, such tightly bound excitons are represented by a superposition of electron–hole pair states with a momentum spread of ∼ℏ/aB. To include excitonic effects on the measured orbital magnetic moment, we average the orbital magnetic moment for electron–hole pair Bloch states over a finite range around the ±K-points (Supplementary Methods 1). We find that to obtain the experimentally observed magnetic moment of 4.3μB using this model, we need to choose aB ∼1.3 nm, which is in excellent agreement with the predicted values for TMDs. We emphasize that using the same three-band tight-binding model to calculate the intercellular contribution for free electron–hole pairs at ±K-points yields a splitting of ∼2μBBz. We therefore conclude that an explanation of the observed values of the magnetic moment requires that the strongly bound nature of the excitons is taken into account. We expect sample-to-sample variations in the measured magnetic moment, originating either from the dielectric environment dependence of the exciton Bohr radius or the strain dependence of the band structure31. However, despite varying estimates for the exciton binding energy, the majority of the experiments on WSe2 monolayers report rather similar exciton emission energies17,22. We expect WSe2 flakes exhibiting an exciton resonance at ∼710 nm to have a similar exciton Bohr radius and magnetic moment.
To calculate the intercellular orbital magnetic moment for the two bands, we use the third-nearest neighbour three-band tight-binding parameters for WSe2 (ref. 9), which reproduces the first-principles calculation for the conduction and valence bands in the entire Brillouin zone. As discussed earlier, the optical emission and absorption in TMDs near the band edge have been shown to stem from strongly bound excitons with a Bohr radius (aB) of the order of 1 nm (ref. 18). In reciprocal space, such tightly bound excitons are represented by a superposition of electron–hole pair states with a momentum spread of ∼ℏ/aB. To include excitonic effects on the measured orbital magnetic moment, we average the orbital magnetic moment for electron–hole pair Bloch states over a finite range around the ±K-points (Supplementary Methods 1). We find that to obtain the experimentally observed magnetic moment of 4.3μB using this model, we need to choose aB ∼1.3 nm, which is in excellent agreement with the predicted values for TMDs. We emphasize that using the same three-band tight-binding model to calculate the intercellular contribution for free electron–hole pairs at ±K-points yields a splitting of ∼2μBBz. We therefore conclude that an explanation of the observed values of the magnetic moment requires that the strongly bound nature of the excitons is taken into account. We expect sample-to-sample variations in the measured magnetic moment, originating either from the dielectric environment dependence of the exciton Bohr radius or the strain dependence of the band structure31. However, despite varying estimates for the exciton binding energy, the majority of the experiments on WSe2 monolayers report rather similar exciton emission energies17,22. We expect WSe2 flakes exhibiting an exciton resonance at ∼710 nm to have a similar exciton Bohr radius and magnetic moment.
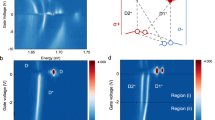
Figure 4a shows the polarization-dependent PL spectra of X− as a function of B in the Faraday geometry. Much like the X0 peak, a splitting of the two circularly polarized components of PL is observed, which increases linearly with B in the Faraday geometry. As in the exciton case, the Voigt geometry measurements did not yield any measurable splitting. Surprisingly, however, the magnitude of the X− splitting was measured to be significantly larger than that of the X0 peak in all the flakes that were studied. As shown in Fig. 4b, the splitting scales linearly with B, with a slope of ∼0.32–0.36 meV T−1, which is more than 25% larger than that of the X0 peak.
a, Normalized polarization-resolved photoluminescence (PL) spectra of the trion (X−) peak as a function of out-of-plane magnetic field (B). b, Linear fit to the splitting extracted from a as a function of B gives a larger value of the trion orbital magnetic moment compared with the exciton (Fig. 2b). c, An illustration of the different orbital magnetic moments of initial |i〉 and final states |f〉 in the X− optical emission process. The blue (red) symbols label the K (−K) valley. The electron–hole exchange energy (δex) results in lower and upper X− states, with the excess electron and the exciton occupying the same valley or the opposite. We assume that the radiative recombination occurs predominantly from the same-valley trion with lower energy. The initial state of the optical emission is thus a trion with exchange-induced magnetic moment, whereas the final state is a Bloch electron in the conduction band with an orbital magnetic moment given by the intercellular circulation. The difference between the two magnetic moments is finite and adds to the intracellular contribution.
A negatively (positively) charged trion is a three-body correlated state comprising a photogenerated electron–hole pair which binds with an electron (hole) in the conduction (valence) band. The binding energy of this three-body state is ∼30 meV, as determined from redshift of the X− peak from the X0 resonance. The PL peak of X− arises from an optical transition in which the initial state is that of the trion whereas the final state has a Bloch electron in the conduction band. Because B-dependent PL splitting is determined by the difference in the orbital magnetic moment between the initial and final states of the optical transition, one expects the B-dependent X0 and X− PL splittings to be identical, as the extra electron in the trion should contribute identically to both the initial and the final state magnetic moment. This simple non-interacting picture is clearly inconsistent with our experimental findings, strongly suggesting the role of interactions in determining the magnetic moment of trions.
Indeed, the degeneracy of the two trion states with centre-of-mass momentum K (−K), which are comprised of an electron in the K (−K) valley and a bright exciton occupying either the same or the opposite valley, is lifted by the electron–hole exchange interaction. The absence of valley coherence of the X− peak in monolayer WSe2 has been attributed to the fast phase-rotation associated with this energy splitting22. Recently, it was theoretically shown that the corresponding exchange-induced modification of the trion dispersion ensures that the trion states with centre-of-mass momentum ∼±K carry a large Berry curvature21. If the trion can be considered as a strongly bound, charged quasi-particle, the exchange-induced Berry curvature Ω(k) will be accompanied by a contribution to the orbital magnetic moment that is given by μ(k) = (e/2ℏ)Ω(k)δex for k ≃ ±K; here δex is the exchange-induced splitting of the trion resonances. Because this additional contribution to the orbital magnetic moment exists only in the initial state of optical emission, it could explain the larger splitting of the X− transition as compared to the X0 transition in our experiments (Fig. 4c), provided that the X− PL originates mainly from the lower trion branch where the exciton and the additional electron occupy the same valley. To estimate the magnitude of splitting based on this additional contribution to magnetic moment, one needs to know the range of momenta of trions involved in the radiative recombination and the Thomas–Fermi screening length. In the absence of this information, we refrain from making a quantitative estimate of the expected trion splitting (Supplementary Methods 2). It should be noted that this unique exchange-induced magnetic moment is very similar to the intercellular contribution in that it stems from the non-trivial geometry of the trion band structure; however, it is optically induced and exists only within the lifetime of trion.
Another expected experimental signature of the electron–hole exchange interaction that acts as an exciton momentum-dependent effective in-plane magnetic field for the valley pseudospin21 is a reduction of the circular dichroism. Indeed the long-range part of intervalley electron–hole exchange has been shown to be an important mechanism for spin relaxation in quantum-well excitons32 and has been recently used to explain valley depolarization in monolayer TMDs (refs 23, 33). An out-of-plane B lifts the valley degeneracy and should, in principle, overcome the valley-mixing due to exchange, thereby increasing the circular dichroism. Our measurements (Fig. 3d) show a sizeable increase in the degree of circular dichroism, by a factor of 1.7–2 at B = 8.4 T as compared to its zero-field value, and are qualitatively consistent with this prediction. However, a quantitative estimation of this increase is not easy, as it depends on the details of relaxation processes following a non-resonant excitation in a PL experiment.
The observation of the valley Zeeman effect validates the predicted 2D band structure of TMDs and establishes the valley degree of freedom as a pseudospin index. The measured value of the magnetic moment clearly establishes that elementary optical spectroscopy of these 2D materials can be understood only by taking into account the consequences of strong electron–hole binding. Conversely, given the electronic band structure determined by a complementary technique such as angle-resolved photoemission spectroscopy (refs 34, 35), it may be possible to use the measured exciton magnetic moment to determine aB. The anomalous magnetic moment of the trion resonance, on the other hand, suggests that it may be possible to observe optical-excitation-induced Berry curvature effects, such as a valley Hall effect that does not require ionization of strongly bound excitons36. A promising future direction to pursue is to couple a TMD monolayer to the photonic modes of a high-quality-factor cavity and to use the exchange coupling of the trion states to create topological states of trion-polaritons, as was recently proposed10.
During the preparation of the manuscript, we became aware of similar results by the University of Washington group37, Cornell group38 and Columbia University group39.
Methods
The samples studied in our experiments were obtained by mechanical exfoliation of WSe2 synthetic crystals onto heavily doped silicon substrates with a 285 nm SiO2 layer on top40,41. Monolayer flakes were identified using their optical contrast. Polarization-resolved photoluminescence (PL) and resonant white-light reflection spectroscopy were performed in a home-built confocal microscope set-up placed in a liquid helium bath cryostat. The sample temperature was 4.2 K and the excitation source was a helium–neon (HeNe) laser at 632.8 nm or a tunable continuous-wave (cw) Ti:sapphire laser. The spot size for the collection wavelength was ∼1 μm, whereas that for 632.8 nm was ∼2–5 μm. Magnetic fields in the range ±8.4 T were applied both parallel and perpendicular to the plane of the sample. Polarization control of the excitation and photoluminescence was done using a liquid crystal retarder calibrated for half and quarter wavelength retardance at the exciton and trion wavelengths.
The magnetic-field-dependent PL and differential reflectance spectra were measured using a high-resolution spectrometer grating (1,500 l mm−1, 750 mm dispersing length) with a resolution of ∼30 μeV, providing a high degree of confidence over the peak position. The PL spectra were fitted using a single Lorentzian peak, together with a cubic polynomial capturing any broad background contribution. As the extracted splitting depends only on the peak position, it is rather insensitive to the actual fitting function; as was verified by trying other lineshapes, such as Gaussian and Voigt. The error in the peak position of the fit was then used to estimate the error in the observed value of orbital magnetic moment for both the exciton and the trion. The reflectance data for the exciton was fitted using an admixture of absorptive and dispersive lineshapes in addition to a linear background.
References
Mak, K. F., Lee, C., Hone, J., Shan, J. & Heinz, T. F. Atomically thin MoS2: A new direct-gap semiconductor. Phys. Rev. Lett. 105, 136805 (2010).
Splendiani, A. et al. Emerging photoluminescence in monolayer MoS2 . Nano Lett. 10, 1271–1275 (2010).
Cao, T. et al. Valley-selective circular dichroism of monolayer molybdenum disulphide. Nature Commun. 3, 887 (2012).
Zeng, H., Dai, J., Yao, W., Xiao, D. & Cui, X. Valley polarization in MoS2 monolayers by optical pumping. Nature Nanotech. 7, 490–493 (2012).
Mak, K. F., He, K., Shan, J. & Heinz, T. F. Control of valley polarization in monolayer MoS2 by optical helicity. Nature Nanotech. 7, 494–498 (2012).
Di, X., Chang, M-C. & Niu, Q. Berry phase effect on electronic properties. Rev. Mod. Phys. 82, 1959–2007 (2010).
Xiao, D., Liu, G-B., Feng, W., Xu, X. & Yao, W. Coupled spin and valley physics in monolayers of MoS2 and other group-VI dichalcogenides. Phys. Rev. Lett. 108, 196802 (2012).
Xu, X., Wang, Y., Di, X. & Heinz, T. F. Spins and pseudospins in layered transition metal dichalcogenides. Nature Phys. 10, 343–350 (2014).
Liu, G-B., Shan, W-Y., Yao, Y., Yao, W. & Xiao, D. Three-band tight-binding model for monolayers of group-VIB transition metal dichalcogenides. Phys. Rev. B 88, 085433 (2013).
Karzig, T., Bardyn, C-E., Lindner, N. & Refael, G. Topological polaritons from quantum wells in photonic waveguides or microcavities. Preprint at http://arXiv.org/abs/1406.4156v1 (2014).
Thonhauser, T., Ceresoli, D., Vanderbilt, D. & Resta, R. Orbital magnetization in periodic insulators. Phys. Rev. Lett. 95, 137205 (2005).
Ceresoli, D., Thonhauser, T., Vanderbilt, D. & Resta, R. Orbital magnetization in crystalline solids: Multi-band insulators, Chern insulators, and metals. Phys. Rev. B. 74, 024408 (2006).
Xiao, D., Yao, W. & Niu, Q. Valley-contrasting physics in graphene: Magnetic moment and topological transport. Phys. Rev. Lett. 99, 236809 (2007).
Yao, W., Xiao, D. & Niu, Q. Valley-dependent optoelectronics from inversion symmetry breaking. Phys. Rev. B 77, 235406 (2008).
Qiu, D. Y., da Jornada, F. H. & Louie, S. G. Optical spectrum of MoS2: Many-body effects and diversity of exciton states. Phys. Rev. Lett. 111, 216805 (2013).
Stroucken, T. & Koch, S. W. Optically bright p-excitons indicating strong Coulomb coupling in transition-metal dichalcogenides. Preprint at http://arXiv.org/abs/1404.4238v3 (2014).
He, K. et al. Tightly bound excitons in monolayer WSe2 . Phys. Rev. Lett. 113, 026803 (2014).
Ye, Z. et al. Probing excitonic dark states in single-layer tungsten disulphide. Nature 513, 214–218 (2014).
Chernikov, A. et al. Exciton binding energy and nonhydrogenic Rydberg series in monolayer WS2 . Phys. Rev. Lett. 113, 076802 (2014).
Wang, G. et al. Non-linear optical spectroscopy of excited exciton states for efficient valley coherence generation in WSe2 monolayers. Preprint at http://arXiv.org/abs/1404.0056v1 (2014).
Yu, H., Liu, G-B., Gong, P., Xu, X. & Yao, W. Dirac cones and Dirac saddle points of bright excitons in monolayer transition metal dichalcogenides. Nature Commun. 5, 3876 (2014).
Jones, A. M. et al. Optical generation of excitonic valley coherence in monolayer WSe2 . Nature Nanotech. 8, 896–869 (2013).
Glazov, M. M. et al. Exciton fine structure and spin decoherence in monolayers of transition metal dichalcogenides. Phys. Rev. B 89, 201302(R) (2014).
Kormányos, A. et al. Monolayer MoS2: Trigonal warping, the valley, and spin–orbit coupling effects. Phys. Rev. B 88, 045416 (2013).
Kośmider, K., González, J. W. & Fernández-Rossier, J. Large spin splitting in the conduction band of transition metal dichalcogenide monolayers. Phys. Rev. B 88, 245436 (2013).
Sallen, G. et al. Robust optical emission polarization in MoS2 monolayers through selective valley excitation. Phys. Rev. B 86, 081301(R) (2012).
Rostami, H., Moghaddam, A. G. & Asgari, R. Effective lattice Hamiltonian for monolayer MoS2: Tailoring electronic structure with perpendicular electric and magnetic fields. Phys. Rev. B 88, 085440 (2013).
Cai, T. et al. Magnetic control of the valley degree of freedom of massive Dirac fermions with application to transition metal dichalcogenides. Phys. Rev. B 88, 115140 (2013).
Rose, F., Goerbig, M. O. & Piéchon, F. Spin- and valley-dependent magneto-optical properties of MoS2 . Phys. Rev. B 88, 125438 (2013).
Chu, R-L. et al. Valley-splitting and valley-dependent inter-Landau-level optical transitions in monolayer MoS2 quantum Hall systems. Phys. Rev. B 90, 045427 (2014).
Zhang, C., Wang, H., Chan, W., Manolatou, C. & Rana, F. Absorption of light by excitons and trions in monolayers of metal dichalcogenide MoS2: Experiments and theory. Phys. Rev. B 89, 205436 (2014).
Maialle, M. Z., de Andrada e Silva, E. A. & Sham, L. J. Exciton spin dynamics in quantum wells. Phys. Rev. B 47, 15776 (1993).
Yu, T. & Wu, M. W. Valley depolarization due to intervalley and intravalley electron–hole exchange interactions in monolayer MoS2 . Phys. Rev. B 89, 205303 (2014).
Zhang, Y. et al. Direct observation of the transition from indirect to direct bandgap in atomically thin epitaxial MoSe2 . Nature Nanotech. 9, 111–115 (2014).
Jin, W. et al. Direct Measurement of the thickness-dependent electronic band structure of MoS2 using angle-resolved photoemission spectroscopy. Phys. Rev. Lett. 111, 106801 (2013).
Mak, K. F., McGill, K. L., Park, J. & McEuen, P. L. The valley Hall effect in MoS2 transistors. Science 344, 1489–1492 (2014).
Aivazian, G. et al. Magnetic control of valley pseudospin in monolayer WSe2. Preprint at http://arXiv.org/abs/1407.2645 (2014).
MacNeill, D. et al. Valley degeneracy breaking by magnetic field in monolayer MoSe2. Preprint at http://arXiv.org/abs/1407.0686v1 (2014).
Li, Y. et al. Valley splitting and polarization by the Zeeman effect in monolayer MoSe2. Preprint at http://arXiv.org/abs/1409.8538v1 (2014).
Novoselov, K. S. et al. Two-dimensional atomic crystals. Proc. Natl Acad. Sci. USA 102, 10451–10453 (2005).
Radisavljevic, B., Radenovic, A., Brivio, J., Giacometti, V. & Kis, A. Single-layer MoS2 transistors. Nature Nanotech. 6, 147–150 (2011).
Acknowledgements
We acknowledge many enlightening discussions with W. Yao, particularly regarding the role of the intracellular current and electron–hole exchange in optical excitations in TMDs. This work is supported by NCCR Quantum Science and Technology (NCCR QSIT), a research instrument of the Swiss National Science Foundation (SNSF).
Author information
Authors and Affiliations
Contributions
A.S. and M.S. carried out the optical measurements. A.V.A., D.S.L. and A.K. prepared the samples. A.S. and A.I. supervised the project and analysed the experimental data. All authors contributed extensively to this work.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Information (PDF 919 kb)
Rights and permissions
About this article
Cite this article
Srivastava, A., Sidler, M., Allain, A. et al. Valley Zeeman effect in elementary optical excitations of monolayer WSe2. Nature Phys 11, 141–147 (2015). https://doi.org/10.1038/nphys3203
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys3203
This article is cited by
-
Realization of large-area ultraflat chiral blue phosphorene
Nature Communications (2024)
-
Proposal for valleytronic materials: Ferrovalley metal and valley gapless semiconductor
Frontiers of Physics (2024)
-
Inheritance of the exciton geometric structure from Bloch electrons in two-dimensional layered semiconductors
Frontiers of Physics (2024)
-
Excitonic devices based on two-dimensional transition metal dichalcogenides van der Waals heterostructures
Frontiers of Chemical Science and Engineering (2024)
-
Ferromagnetism emerged from non-ferromagnetic atomic crystals
Nature Communications (2023)