Abstract
The cosmological applications of atomic clocks1,2,3 so far have been limited to searches for the uniform-in-time drift of fundamental constants4. We point out that a transient-in-time change of fundamental constants can be induced by dark-matter objects that have large spatial extent, such as stable topological defects5 built from light non-Standard Model fields. Networks of correlated atomic clocks, some of them already in existence6, such as the Global Positioning System, can be used as a powerful tool to search for topological defect dark matter, thus providing another important fundamental physics application for the ever-improving accuracy of atomic clocks. During the encounter with an extended dark-matter object, as it sweeps through the network, initially synchronized clocks will become desynchronized. Time discrepancies between spatially separated clocks are expected to exhibit a distinct signature, encoding the defect’s space structure and its interaction strength with atoms.
Similar content being viewed by others
Main
Despite solid evidence for the existence of dark matter (∼25% of the global energy budget in the Universe and ρDM ≃ 0.3 GeV cm−3 in the neighbourhood of the Solar system7), its relationship to particles and fields of the Standard Model (SM) remains a mystery. Although searches for particle dark matter (DM) are being actively pursued8, there is also significant interest in alternatives, among which is DM composed from very light fields. Depending on the initial field configuration at early cosmological times, such light fields could lead to dark matter via coherent oscillations around the minimum of their potential, and/or form non-trivial stable field configurations in physical three-dimensional space if their potential allows such a possibility. This latter option, which we will generically refer to as topological defects (TDs), is the main interest of our paper. The light masses of fields forming the TDs could lead to a large, indeed macroscopic, size for a defect. Their encounters with the Earth, combined with the DM–SM coupling, can lead to novel signatures of dark matter expressed generically in terms of ‘transient effects’. These effects, coherent on the scale of individual detectors, are temporary shifts in the frequencies and phases of measuring devices, rather than large energy depositions as is the case for microscopic DM. In this paper we suggest the possibility of a new search technique for the topological defect dark matter (TDM), based on a network of atomic clocks.
Atomic clocks are arguably the most accurate scientific instruments ever built, reaching a 10−18 fractional inaccuracy1,2. Attaining this accuracy requires that the quantum oscillator be well protected from environmental noise and that perturbations be well controlled and characterized. This opens the intriguing prospect of using clocks to study subtle effects, and it is natural to ask if such accuracy can be harnessed for dark-matter searches.
To put our discussion on concrete grounds, we introduce a collection of light fields beyond the SM that can form TDs of different dimensionality: monopoles (0D), strings (1D) and domain walls (2D). The exact nature of such defects depends on the composition of the dark sector and on the self-interaction potential5. For this paper we take a simplified approach, calling ϕ a generic light field from the dark sector, whether it be scalar or vector, that forms a network of TDs at some early stage of cosmological history. The transverse size of the defect is determined by the field Compton wavelength d, which is in inverse relation to the typical mass scale of the light fields, d ∼ ℏ/(mϕc). The fields we are interested in are ultralight: for an Earth-sized defect, the mass scale is 10−14 eV . In our simplified approach we capture only the gross features of TDs (ref. 5), and call A the amplitude of the field change between inside and outside a TD, A = ϕinside − ϕoutside, also choosing the outside value of the field to be zero.
The energy density of TDM averaged over a large number of defects is controlled by the energy density inside the defect, ρinside ∼ A2/d2, and the average distance between the defects, L, through the natural scaling relation:

where n = 0,1,2 for monopoles, strings or domain walls, and we measure A in units of energy.
The right combination of parameters can give a significant contribution to, or even saturate ρDM. The average time between ‘close encounters’ with TDs, r ≤ d, is set by the galactic velocity of such objects vg,

The velocity of galactic objects around the Solar system is an input parameter that is relatively well known, and for the purpose of estimates one can take vg ≃ 10−3 × c ≈ 300 km s−1. If the parameter  is of the order of a few years or less, then it is reasonable to think of a detection scheme for TD crossing events.
is of the order of a few years or less, then it is reasonable to think of a detection scheme for TD crossing events.
The most crucial question is how the fields forming the defect interact with the SM. All possible types of interaction between TDs and SM fields can be classified using the so-called ‘portals’, a collection of gauge-invariant operators of the SM coupled with the operators from the dark sector9. Throughout the remainder of this paper, we will be interested in a more general form of the SM–TD interaction, in the form of the quadratic scalar portal,

Because inside the TD, by assumption, ϕ2 → A2 and outside ϕ2 → 0, this portal renormalizes masses and couplings only when the TD core overlaps with the quantum device. Here me, p and ψe, p are electron and proton masses and fields, and Fμν are electromagnetic tensor components. The appearance of high-energy scales ΛX in the denominators of (2) signifies the effective nature of these operators, implying that at these scales the scalar portals will be replaced by some unspecified fundamental theory (in the same way as the electroweak theory of the SM replaces the effective four-fermion weak interaction at the electroweak scale). The SM field dependence in (2) replicates corresponding pieces from the SM sector Lagrangian density, thus leading to the identification (the second line of equation (2)) of how masses and the fine-structure constant α are modulated by the TD. Thus, for every coupling constant and SM particle mass scale X one has, to first order in ϕ2,

A quadratic (as opposed to linear) dependence on ϕ leads to weakening of the constraints imposed by precision tests of gravitational interactions10. Both direct laboratory and astrophysical constraints on ΛX do not exceed ∼10 TeV. Further background information on TDM, the types of interaction with the SM, and plausible scenarios for its abundance are provided in the Supplementary Information. In particular, we present an explicit example of the so-called Abrikosov–Nielsen–Olesen string defect11,12, with an increased value of α inside its core.
The main consequence of the interaction (2) is a temporary shift of all masses and frequencies inside the TD. Thus, the signature we are proposing to search for is a transient variation of fundamental constants. In the limit of large τ, when the size of a TD is on astronomical scales, the effect of (2) becomes identical to variations of couplings and masses over time with  , in which case all the existing terrestrial constraints immediately apply4. In addition, during the TD crossing there is a new force acting on massive bodies, giving a transient signature that can be explored with sensitive graviometers. Also, there are other ways of coupling TDs to the SM, such as the so-called axionic portals, ∂μϕ/fa × Jμ, where Jμ is the axial-vector current. This would lead to a transient ‘loss’ of rotational/Lorentz invariance, and can be searched for with sensitive atomic magnetometers13,14. By design, atomic clocks are less sensitive to the coupling to spin, and for that reason we concentrate on (2).
, in which case all the existing terrestrial constraints immediately apply4. In addition, during the TD crossing there is a new force acting on massive bodies, giving a transient signature that can be explored with sensitive graviometers. Also, there are other ways of coupling TDs to the SM, such as the so-called axionic portals, ∂μϕ/fa × Jμ, where Jμ is the axial-vector current. This would lead to a transient ‘loss’ of rotational/Lorentz invariance, and can be searched for with sensitive atomic magnetometers13,14. By design, atomic clocks are less sensitive to the coupling to spin, and for that reason we concentrate on (2).
Clocks tell the time by counting the number of oscillations and multiplying this by a predefined period of oscillation, 1/(2πω0), where ω0 is the fixed unperturbed clock frequency. The experimentally relevant quantity is the total phase accumulated by the quantum oscillator,  then apparently the device time reading is ϕ0(t)/ω0. A TD would shift the oscillator frequency and thereby affect the phase or the time reading,
then apparently the device time reading is ϕ0(t)/ω0. A TD would shift the oscillator frequency and thereby affect the phase or the time reading,  where δω(t′) is the variation in quantum oscillator frequency caused by the TD. We parameterize δω(t) = gf(t), where g ∝ A2/Λ2 is the coupling strength and f(t) ∝ |ϕ(r − vgt)|2 is a time-dependent envelope (r is the clock position), so that
where δω(t′) is the variation in quantum oscillator frequency caused by the TD. We parameterize δω(t) = gf(t), where g ∝ A2/Λ2 is the coupling strength and f(t) ∝ |ϕ(r − vgt)|2 is a time-dependent envelope (r is the clock position), so that  .
.
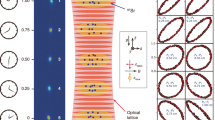
Suppose we compare the phases of two identical clocks separated by a distance l (see Fig. 1), which encounter a domain-wall-type TD. Because the TD propagates through the network with a speed vg, the second clock would be affected by the TD at a later time, with a time delay l/vg. Formally, the phase difference (or apparent time discrepancy Δt) between the clocks reads

By monitoring the correlated time difference Δt(t) between the two clocks, one could search for TDM. Before the arrival of the TD at the first clock, the phase difference is zero, as the clocks are synchronized. As the TD passes the first clock, it picks an additional phase difference |Δφ|max = |g|d/vg. Δφ(t) stays at that level while the TD travels between the two clocks. Finally, as the TD sweeps through the second clock, the phase difference vanishes. In this illustration we assumed that d ≪ l ≪ L. In the limit of d ≲ l, frequency (instead of time) comparison can be more accurate.
We may further relate the TD-induced frequency shift to transient variation of the fundamental constants. The instantaneous clock frequency shift may be parameterized as

where X runs over the fundamental constants. The dimensionless sensitivity coefficients KX are known from atomic and nuclear structure calculations15. It is important to note that different types of clocks exhibit sensitivity to different combinations of fundamental constants, with optical clocks being mostly sensitive to α and microwave clocks also being sensitive to nuclear couplings (Supplementary Information). The energy density stored in the TD and various couplings enters implicitly through a time-varying deviation, δX(t) ∝ |ϕ(r − vgt)|2, of the fundamental constant from its nominal value. Then the two clocks will be desynchronized by

Here we used equation (1) and the fact that contributions to the Lagrangian (2) factorize into SM and TDM parts. Notice that this result does not depend on a specific class of TDs.
In practice, one needs to dissect the TD-induced desynchronization (4) from the various noise sources present in quantum devices and the link connecting the two clocks. We neglect link noise. We assume that the TD thickness d is much smaller than the distance between the clocks, as shown in Fig. 1. One would need to resolve the ‘hump’ in the presence of background noise. Suppose we compare the clock readings every T seconds; then the total number of measurements of non-zero phase difference is Nm = l/(vgT). For a terrestrial network with an arm length of l ∼ 10,000 km, the TD sweep takes 30 s, so one could make 30 measurements, sampled every second.
Because the clocks are identical and statistically independent, the variance 〈Δφ(t)2〉 − 〈Δφ(t)〉2 = 2Rφ(T), where Rφ(T) is the phase auto-covariance function16. It can be estimated from the commonly reported Allan variance σy(T), which characterizes the fractional instability of the clock frequency17: Rφ(T) ≈ (ω0T)2 σy2(T). Thereby the uncertainty due to a single clock comparison is  . As we carry out Nm = l/(vgT) measurements, the statistical uncertainty is reduced further by
. As we carry out Nm = l/(vgT) measurements, the statistical uncertainty is reduced further by  .
.
The above argument leads to the signal-to-noise ratio

This ratio scales up with the TD size d, the sensitivity coefficients KX, and the distance between the clocks. See Supplementary Information for a further discussion.
The TD detection confidence would improve both by increasing the number of network nodes and by populating nodes with several clocks of different types. Clearly, when the TD sweep is detected, all the clock pairs should exhibit a time-correlated desynchronization signature associated with the sweep. Different clocks have distinct sensitivities to the variation of the fundamental constants, and this could help in disentangling various couplings in (2) and (3). Moreover, a large number of clocks in a network will help in determining the direction of arrival of the TD, its velocity and spatial extent.
The analysis presented can be generalized to the case of point-like TD (monopoles), which under a gravitational force will behave identically to regular cold dark matter. We illustrate such a case in Fig. 2. Here we assume that the TD is an Earth-scale Gaussian-profile cloud sweeping through a clock network. Individual clocks are perturbed at different times with different amplitudes, depending on the distance to the monopole centre. This leads to a TD-induced phase accumulation,

where R(t) = {X0, Y0, Z0 + vgt} and ri = {xi, yi, zi} are the positions of the TD centre and the ith clock, respectively, and d is the effective radius of the TD. Here we assumed that the TD propagates along the z axis. The coupling is rescaled depending on the clock position gi ≡ gexp{−ρi2/d2}, with ρi = ((X0 − xi)2 + (Y0 − yi)2)1/2 being the impact parameter. This translates into a differential phase accumulation between the clocks, similar to our ‘wall’ example of Fig. 1, but with the step-on and step-off heights depending on the difference of the clock impact parameters. Having several different types of clock at each node of the network will maximize the discovery potential, increasing sensitivity to monopole and string-type objects, especially if their transverse size is much smaller than R⊕. In that case, direct comparison of several clocks within one node is needed. Implementing such a search with several clocks at a single node can be the first step towards a global TDM search effort. Detailed network optimization strategies for TDM searches of varying transverse size d and dimensionality n are left for future investigations.
Simulated response of an Earth-scale constellation of atomic clocks to a 0D Gaussian-profiled topological defect (monopole) of effective radius 0.75R⊕. The monopole centre is displaced from the collision axis by 0.2R⊕. Earth’s centre and the clocks lie in the collision plane. The polar angles of the three clocks are π/2, π, −π/4 in a reference frame centred at the Earth’s centre.
Several networks of atomic clocks are already operational. Perhaps the most well known are the Rb and Cs microwave atomic clocks on-board satellites of the Global Positioning System (GPS) and other satellite navigation systems. We envisage using the GPS constellation as a 50,000-km-aperture dark-matter detector, with added capabilities due to the extensive terrestrial network of atomic clocks on the GPS tracking stations. As TDs sweep through the GPS constellation, satellite clock readings are affected. Because accurate ephemeris satellite data are known, one could easily cross-correlate clock readings in the network. For two diametrically opposed satellites the maximum time delay between clock perturbations would be ∼200 s, assuming a TD sweep with a typical velocity of 300 km s−1. Different types of topological defects (for example, domain walls versus monopoles) would yield distinct cross-correlation signatures. Although the GPS is affected by a multitude of systematic effects—for example, solar flares, temperature and clock frequency modulations as the satellites come in out of Earth’s shadow—none of the conventional effects would propagate with a velocity of 300 km s−1 through the network.
Dark-matter searches can also be implemented with state-of-the art laboratory clocks1,2, using the vast network of atomic clocks at national standards laboratories used for evaluating the TAI timescale3. Moreover, several elements of high-quality optical links for clock comparisons have already been demonstrated in Europe, with a 920 km link connecting two laboratories in Germany6. Furthermore, a caesium fountain clock and a hydrogen maser are planned for installation on the International Space Station in the near future, providing high-quality time and frequency links to several metrology laboratories around the globe18.
As an illustration of sensitivity to the energy scales ΛX of TDM–SM coupling (2), we consider a terrestrial network (l ∼ 10,000 km) of Sr optical lattice clocks which are sensitive to the variation of α with Kα = 6 × 10−2. For these clocks one may anticipate reaching σy(1 s) ∼ 10−18 at T = 1 s measurement intervals. Requiring S/N ∼ 1 in equation (5), substituting fiducial values for ρTDM and vg, and choosing  yr, we plot a sensitivity curve to the energy scale Λα as a function of the defect size in Fig. 3. Here we also show the sensitivity of the GPS constellation (l ∼ 50,000 km, T = 30 s, σy(30 s) ∼ 10−11), assuming that the TDM–SM coupling is dominated by the transient variation of α (Kα = 2). Limits derived from both Sr and GPS networks would greatly exceed the Λ < 10 TeV region excluded by direct laboratory and astrophysical constraints, such as from fifth-force and violation of the equivalence principle searches10.
yr, we plot a sensitivity curve to the energy scale Λα as a function of the defect size in Fig. 3. Here we also show the sensitivity of the GPS constellation (l ∼ 50,000 km, T = 30 s, σy(30 s) ∼ 10−11), assuming that the TDM–SM coupling is dominated by the transient variation of α (Kα = 2). Limits derived from both Sr and GPS networks would greatly exceed the Λ < 10 TeV region excluded by direct laboratory and astrophysical constraints, such as from fifth-force and violation of the equivalence principle searches10.
Terrestrial and space networks of atomic clocks can impose powerful constraints on the characteristic energy scales of dark-matter interactions with baryonic matter (2). Here we show bounds on Λα that may be derived from a terrestrial network of optical lattice clocks and GPS clocks. The horizontal axis is the topological defect size in kilometres and also includes two characteristic TD field rest mass scale values.
References
Chou, C. W., Hume, D. B., Koelemeij, J. C. J., Wineland, D. J. & Rosenband, T. Frequency comparison of two high-accuracy Al+ optical clocks. Phys. Rev. Lett. 104, 070802 (2010).
Bloom, B. J. et al. An optical lattice clock with accuracy and stability at the 10−18 level. Nature 506, 71–75 (2014).
Levine, J. Introduction to time and frequency metrology. Rev. Sci. Instrum. 70, 2567–2596 (1999).
Rosenband, T. et al. Frequency ratio of Al+ and Hg+ single-ion optical clocks; metrology at the 17th decimal place. Science 319, 1808–12 (2008).
Vilenkin, A. Cosmic strings and domain walls. Phys. Rep. 121, 263–315 (1985).
Predehl, K. et al. A 920-Kilometer optical fiber link for frequency metrology at the 19th decimal place. Science 336, 441–444 (2012).
Beringer, J. et al. Review of particle physics. Phys. Rev. D 86, 010001 (2012).
Bertone, G. (ed) Particle Dark Matter: Observations, Models and Searches (Cambridge Univ. Press, 2010).
Essig, R. et al. Dark sectors and new, light, weakly-coupled particles. Preprint at http://arxiv.org/abs/1311.0029 (2013).
Olive, K. A. & Pospelov, M. Environmental dependence of masses and coupling constants. Phys. Rev. D 77, 043524 (2008).
Abrikosov, A. A. On the magnetic properties of superconductors of the second group. Sov. Phys. JETP 5, 1174–1182 (1957).
Nielsen, H. B. & Olesen, P. Vortex line models for dual strings. Nucl. Phys. B 61, 45–61 (1973).
Pospelov, M. et al. Detecting domain walls of axionlike models using terrestrial experiments. Phys. Rev. Lett. 110, 021803 (2013).
Pustelny, S. et al. The Global Network of Optical Magnetometers for Exotic physics (GNOME): A novel scheme to search for physics beyond the Standard Model. Ann. Phys. 525, 659–670 (2013).
Flambaum, V. V. & Dzuba, V. A. Search for variation of the fundamental constants in atomic, molecular, and nuclear spectra. Can. J. Phys. 87, 25–33 (2009).
Allan, D. Statistics of atomic frequency standards. Proc. IEEE 54, 221–230 (1966).
Barnes, J. A. et al. Characterization of frequency stability. IEEE Trans. Inst. Meas. IM-20, 105–120 (1971).
Atomic Clock Ensemble in Space (ACES), http://www.esa.int/SPECIALS/HSF_Research/SEMJSK0YDUF_0.html
Acknowledgements
We would like to thank N. Fortson, P. Graham, J. Hall, M. Murphy, J. Sherman, J. Weinstein and I. Yavin for discussions. This work was supported by the US National Science Foundation, the Natural Sciences and Engineering Research Council of Canada, and the province of Ontario.
Author information
Authors and Affiliations
Contributions
Both authors contributed to the work equally.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Information (PDF 751 kb)
Rights and permissions
About this article
Cite this article
Derevianko, A., Pospelov, M. Hunting for topological dark matter with atomic clocks. Nature Phys 10, 933–936 (2014). https://doi.org/10.1038/nphys3137
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys3137
This article is cited by
-
Experimental realization of a 12,000-finesse laser cavity based on a low-noise microstructured mirror
Communications Physics (2023)
-
Unveiling time-varying signals of ultralight bosonic dark matter at collider and beam dump experiments
Communications Physics (2023)
-
Quantum networks with neutral atom processing nodes
npj Quantum Information (2023)
-
Quantum-limited optical time transfer for future geosynchronous links
Nature (2023)
-
The development of active optical clock
AAPPS Bulletin (2023)