Main

The name ‘soliton’ is meant to convey the particle-like qualities of localized and non-dispersing wave packets, and is often reserved for those solitary waves that pass through one another without changing form. The wave packets studied here are not true solitons owing to the presence of a harmonic confining potential which breaks integrability. Furthermore, as quasi-1D objects, they reside near the border between 1D and 3D, where integrability is also broken. Nonetheless, the proximity to this border does not necessarily affect the soliton dynamics over experimentally relevant timescales. We will thus use the term soliton more generally to refer to non-dispersing wave packets created by a nonlinearity. Although the propagation of individual solitons is now well understood, having been extensively studied both experimentally and theoretically3, their interactions with each other have been much less explored. Although true solitons pass through one another, they nonetheless exhibit an effective interaction produced by interference of the two wave packets, with a force falling off exponentially with separation4. The sign and magnitude of the interaction depends on the relative phase, as was first demonstrated experimentally for optical solitons in both the time5 and spatial6 domains.

Studies of matter-wave solitons have mainly examined properties of single solitons 7,8,9,10, with the study of soliton interactions limited to those occurring in soliton trains8,11 and collisions between multiple solitons resulting from a quench12. We provide further insight into the collisional dynamics of matter-wave solitons through the controlled formation of soliton pairs, and explicitly demonstrate that the discontinuous jump observed in soliton collisions13 is a general property of the nonlinear interaction.

Our methods for producing a degenerate gas of 7Li atoms have been described previously14 and are given in the Methods section. A Bose–Einstein condensate of atoms in the |F = 1, mF = 1〉 state is formed by evaporative cooling at a scattering length of a = +140a0 and is confined in a cylindrically symmetric harmonic trap with radial and axial oscillation frequencies of ωr/2π = 254 Hz and ωz/2π = 31 Hz, respectively. After forming the condensate, a cylindrically focused blue-detuned Gaussian laser beam directed perpendicular to the long axis of the confining potential is used to cut the condensate in half, and acts as a barrier between the two condensates (Fig. 1a). The scattering length is then adiabatically ramped from a = +140a0 to a = −0.57a0 via the broadly tunable Feshbach resonance of the |F = 1, mF = 1〉 state15 to form a pair of solitons with a centre-to-centre separation of 26 μm and near equal amplitude (N ≈ 28,000 atoms/soliton). Once the pair is formed, the barrier is quickly (t < 60 ns) turned off. Thus, the solitons suddenly find themselves at the classical turning points of the harmonic trap and begin to accelerate towards the centre. We confirm that these wave packets are non-dispersive by observing the absence of expansion when the axial confinement frequency is suddenly reduced, whereas a wave packet with a small, repulsive scattering length rapidly expands (Supplementary Fig. 1).

Figure 1: Schematic of the experiment and images of phase-dependent collisions.
figure 1

a, Schematic showing the process of soliton-pair formation. Beginning with the bottom frame, the potential is shown as a black-dashed line with a condensate density profile shown in solid blue. After forming a condensate, the barrier is turned on to split the condensate in two. The scattering length is ramped from a = +140a0 to a = −0.57a0 and pairs of solitons are formed. The barrier is quickly turned off, and the solitons move towards the centre of the trap. b, Time evolution of a soliton pair (N/Nc = −0.53) after the barrier is turned off. Solitons are accelerated towards the centre of the trap and collide at a quarter-period (τ = 2π/ωz = 32 ms). The density peak appearing at the centre-of-mass indicates that this is an in-phase (Δϕ ≈ 0) collision. c, Similar to b, except the density node appearing at the centre-of-mass indicates an out-of-phase (Δϕ ≈ π) collision.

Full size image

We find that the two solitons interact with a randomly distributed relative phase over different experimental runs, so we use a minimally destructive phase-contrast imaging method, polarization phase-contrast imaging16, to obtain multiple images of the soliton pair as they oscillate and collide in the harmonic trap. This imaging technique plays a key role in observing and interpreting the collisional dynamics because it allows us to take multiple images within a single realization of the experiment (Methods).

We infer the relative phase difference through comparison with numerical simulations of the 1D and 3D Gross–Pitaevskii equations (GPEs). Figure 1b, c shows two experimental realizations in which the relative phase difference is Δϕ ≈ 0 and Δϕ ≈ π, respectively. Images are taken every one eighth of a trap period (τ = 32 ms). Figure 1b, c shows trajectories over one complete period, corresponding to two collisions. For Δϕ ≈ 0, a clear anti-node is observed during the collision at the centre, giving the appearance of an attractive interaction, whereas in the Δϕ ≈ π case, interference results in a central node and the interaction between solitons is effectively repulsive.

The quasi-1D nature of our system, coupled with the ability to form soliton pairs with a strong nonlinearity, allows us to observe the rich dynamics inherent in a system at the edge of integrability. The strength of the nonlinearity is parametrized by N/Nc, where Nc = 0.67ar/a is the critical atom number, , and m is the atomic mass. A soliton is unstable to collapse for N > |Nc| (ref. 17). Although collapse is relevant only for attractive interactions, we also use N/Nc to parametrize the strength of the nonlinearity for repulsive condensates. For values of N/Nc = −0.53, we observe that in-phase collisions (Δϕ ≈ 0) sometimes result in annihilation (Fig. 2a) or fusion of the soliton pair (Fig. 2b), although more typically we observe partial collapses in which the atom number and the oscillation amplitude are reduced after multiple collisions. These effects can be understood as the result of density-dependent inelastic collisions in which the system becomes effectively 3D (refs 18, 19, 20). Similar effects have been observed in nonlinear optics21. We find from the GPE simulations that collisions with Δϕ = 0 and N/Nc < −0.5 are unstable to collapse. The observation that collisions with Δϕ ≈ 0 do not always lead to collapse (for example, Fig. 1b) is consistent with the shot-to-shot variation in N of ∼20% (Methods). For the same nonlinearity, out-of-phase collisions (Δϕ ≈ π) are extremely robust against collapse and survive many oscillations in the trap, as predicted theoretically18,20,22. Although on the edge of integrability, we have observed solitons with N/Nc = −0.53 and Δϕ = π to survive more than 20 collisions (Fig. 2c).

Figure 2: Phase-dependent collisional dynamics.
figure 2

a, A collision between two solitons (N/Nc = −0.53) resulting in collapse. During the collision, the density exceeds a critical value and becomes unstable against collapse. No remaining atoms are observed. b, A collision between two solitons (N/Nc = −0.53) resulting in a merger. The remaining atom number after the collision is the same as that of a single soliton before the collision. c, Out-of-phase collisions between two solitons after allowing them to oscillate for ten trap periods.

Full size image

The defining property of solitons passing through one another without change of shape, amplitude, or speed seems to be at odds with the observations presented in Fig. 1c, where solitons with Δϕ = π apparently reflect from one another. This paradox is resolved by noting that the effective interaction is a wave phenomenon4, where interference gives the appearance of reflection when, in fact, the solitons do pass through one another. We experimentally demonstrate this by forming pairs of solitons with unequal atom numbers by removing atoms from one side using a short duration, near-resonant pulse of light before ramping the field to form solitons. This allows us to identify, or tag, a particular soliton and to follow its trajectory before and after the collision. In Fig. 3 we show one such realization, in which a soliton pair was formed with a 2:1 ratio in atom number. Although a minimum does appear between the solitons during the collision, as expected for an effectively repulsive interaction, the trajectories show that they do pass through one another. The experiment does not rule out the possibility that the solitons reflect while exchanging particles during the collision. The 1D GPE simulations, however, demonstrate that particle exchange is a relatively small effect for the large collisional velocity in our experiment, in agreement with previous theoretical studies19,20.

Figure 3: Tagged trajectory of soliton collision.
figure 3

A pair of solitons is formed with a ratio of 2:1 in atom number. The resultant collision appears to be repulsive, indicated by the density minimum appearing between the pair at t = 1/4τ and 3/4τ. However, by following the trajectories of individual solitons, we observe that they actually pass through one another in the course of each collision.

Full size image

A close inspection of the oscillations shown in Fig. 2c reveals that the solitons oscillate at a higher frequency than the usual dipole frequency, ωz. This increased oscillation frequency is a consequence of a jump in the phase of the trajectories of the colliding, harmonically confined, solitons. Without axial confinement, the phase jump manifests as a sudden change in position relative to the original trajectory, as shown in the simulation of Fig. 4a. Although the phase of the trajectory is modified by the collision, the speed of the soliton following the collision is not. The jump is a consequence of the nonlinearity of the system2, and was first observed with optical solitons13.

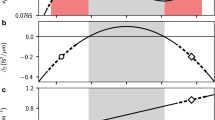
Figure 4: Frequency shift due to mean-field interaction between solitons.
figure 4

a, Simulated trajectory without an axial potential, in arbitrary units (a.u.). The dashed-white lines show the soliton trajectories in the absence of interaction. b, The harmonic potential energy per atom, U(t) (Methods), is plotted for different strengths of the nonlinearity. Each data point is the mean of five different experimental runs (blue points). The red lines are the results of a fit to determine the oscillation frequency. The error bars correspond to the standard error of the mean. c, The relative frequency shifts determined from the fits to the experimental data are plotted versus the nonlinearity strength (blue squares). The error bars correspond to the standard error of the fit for Δωz/ωz. The error bars for N/Nc are the standard error of the mean for five measurements of N. In addition, the systematic uncertainty in N/Nc is estimated to be 23% for |a| ≃ 0.5a0 (Methods). Relative shifts were also determined by numerically solving the 1D GPE (red points). An analytical approximation determined solely by the incoherent density–density terms in the GPE is shown by the dashed line, as described in Methods.

Full size image

We studied this effect by measuring the oscillation frequency of pairs of solitons for different strengths and sign of the nonlinearity (a condensate with a > 0 also oscillates without dispersion in the presence of harmonic confinement23). At each value of N/Nc, the measured axial density profiles were used to calculate the average harmonic potential energy per atom at different times during the oscillation, and subsequently fitted to determine the oscillation frequency (Methods). Oscillations for N/Nc = −0.53, N/Nc = 0 and N/Nc = +0.55 are plotted in Fig. 4b for a total of three trap periods, in each case. Because the potential energy per atom is plotted, a total of six oscillations are observed. The frequency for the attractive (repulsive) interactions clearly leads (lags) when compared to the non-interacting (a = 0) case. The relative frequency shifts are plotted in Fig. 4c and we find them to be in reasonable agreement with numerical simulations obtained by solving the 1D GPE. We observe that the relative shift also provides a sensitive measurement of the zero crossing, which is in excellent agreement with a previous determination15. The frequency shift is independent of Δϕ, indicating that it is unrelated to the phase-dependent interactions previously discussed.

We have developed a simple analytical approximation to calculate the frequency shift. The shift arises from the mean-field interaction in which one soliton changes the potential landscape experienced by the other soliton. The phase shift is dominated by the incoherent (density–density) terms in the interaction, and we neglect all other interaction terms in the GPE in comparison. This approximation is valid for relatively weak nonlinearity and for fast-moving solitons (Methods). Although a phase shift is expected in integrable systems, the analytical approximation accounts for harmonic confinement, thus providing an estimate of the frequency shift for either sign of the nonlinearity. The analytically predicted relative frequency shift is in which z0 is the oscillation amplitude of a single soliton and az (ar) is the axial (radial) harmonic oscillator length. N/Nc is negative for a < 0. This approximation provides a simple, intuitive picture. For a < 0, the attraction between atoms accelerates the solitons as they approach one another, and decelerates them as they move away. The same occurs for a > 0, but with opposite sign. A similar effect has been observed for repulsive condensates, in which oscillations of one condensate induced motion in the other24,25.

Our studies elucidate the role of integrability, relative phase, spatial dimensionality, and mean-field interactions in soliton collisions. A natural extension of this work would involve control over the relative phase between solitons, and better control of the strength of the nonlinearity. This would enable us to study collisions in a more controlled manner, providing the ability to further explore the transition between integrable and non-integrable systems, and to study the formation of soliton molecules26. Finally, this geometry may be applicable to atom soliton interferometry, demonstrated recently using a Bragg beam splitter27 rather than the tunnel barrier adopted in our geometry.

Methods

Apparatus.

The primary difference between the apparatus used here and that which was described previously14 is that a pair of perpendicularly oriented laser beams, derived from a single fibre laser operating at 1,070 nm, provide cylindrically symmetric harmonic confinement. The beam is divided into two separate paths, directed parallel and perpendicular to the magnetic field axis, and focused at the atoms to 1/e2 radii of 28 μm and 105 μm, respectively.

The magnetic field is controlled using a pair of coils in the Helmholtz configuration, and allows us to vary the scattering length across a broad region. Initially, the BEC is formed at a field of 716 G, corresponding to a scattering length of a ≈ 140a0 (ref. 28). Once the BEC is formed, a blue-detuned Gaussian beam is turned on to cut the condensate in half and act as a high barrier between the two halves. The field is adiabatically ramped down (t = 750 ms) to a final scattering length of a = −0.57a0. We find experimentally that this procedure produces two solitons, which interact with a randomly distributed relative phase.

To measure the oscillation frequencies for different nonlinearities, the final scattering length is varied between a = −0.57a0 and a = + 0.37a0, corresponding to nonlinear strengths of N/Nc = −0.53 and N/Nc = +0.55, respectively.

The barrier is a cylindrically focused beam, blue-detuned by 900 GHz from the 2S–2P resonance, with a 1/e2 radius of 2 mm perpendicular to the condensate, and a 1/e2 radius of 5.6 μm along the condensate axis. A barrier height of approximately 2 μK was used to split the condensate, and to maintain a centre-to-centre separation of 26 μm between solitons.

Polarization phase-contrast imaging (PPCI) was used to minimally perturb the atoms, allowing us to take multiple images during a single experimental run. Because the relative phase of solitons varies between experimental runs, the use of this technique was crucial for interpreting the collisional dynamics. PPCI exploits the birefringence of the scattered light from atoms in a strong magnetic field. The scattered light is interfered with the probe light using a linear polarizer. The resulting image is simply related to the column density distribution16. With this technique the laser may be far detuned from resonance (35Γ in this case, where Γ = 5.9 MHz), minimizing the number of photons scattered during the imaging process. Furthermore, the 1/e2 beam radius of approximately 11 mm provides a uniform intensity profile across the soliton pair so that any phase shift imprinted on the solitons from the imaging beam is common for the pair.

Oscillation frequency.

The axial density, n1D(z, t), was calculated for each image and used to determine the potential energy per atom from:

Analytical approximation of frequency shift.

The quasi-1D GPE is:

in which g1d = 2ℏ2a/mar2. Here, a, as above, is the atomic scattering length, and az(ar) is the axial (radial) harmonic oscillator length29. In the absence of the nonlinear interaction, the two-soliton state is modelled by ψ = ψ1 + eiϕψ2, where ψi is:

We have introduced the position coordinate ξ such that ξ = ξ1 = − ξ2 = z0 sin(ωzt), which defines a pair of symmetric Gaussians in the harmonic trap. In the limit of large impact speed (that is, z0 ≫ az) the interaction Hamiltonian becomes:

in which the coherent interaction terms are neglected owing to the fast spatial-phase oscillations between the rapidly moving solitons. We treat the interaction-induced shift as a small perturbation, and write the soliton motion as ξ(t) = z0 sin(ωzt) + Δξ. The equation of motion for the perturbation Δξ is30:

in which Nm serves as the effective mass of the soliton and the factor 1/2 is due to the identity ξ ≡ (ξ1 − ξ2)/2. By substituting equations (1) and (2) in (3), we find that the total spatial jump due to the density–density interaction is:

and the corresponding shift in the oscillation frequency is:

The approximate analytical approach presented here applies to a broad class of pulses in generic models, matching the known results for integrable ones.

Uncertainties.

The uncertainty in the strength of the nonlinearity is due to the uncertainty in the atom number, N, the determination of the scattering length, a, and the radial trap frequency, ωr. The uncertainty in N arises from 20% shot-to-shot variation in N and a systematic uncertainty of 12% due to our ability to discern atoms from the background. To measure ωr, the trap intensity was modulated near the radial trap frequency and the resultant loss in atom number, from heating, was measured. The uncertainty in ωr determined from a Lorentzian fit to the data is <1%. The mapping of a versus B has been previously determined, with our region of interest being near the zero crossing15. A linear fit to the data near the zero crossing gives a slope of 0.08(1) a0/G and a zero crossing at B0 = 543.6(1) G, with the uncertainties derived from a systematic uncertainty in the field calibration of 0.1 G. This gives a systematic uncertainty in a of 20% for |a| ≃ 0.5a0. Thus, the statistical and systematic uncertainties in the strength of the nonlinearity are 20% and 23%, respectively, for |a| ≃ 0.5a0.