Abstract
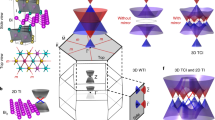
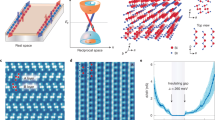
The hallmark of a topologically insulating state of matter in two dimensions protected by time-reversal symmetry is the existence of chiral edge modes propagating along the perimeter of the sample. Among the first systems predicted to be a two-dimensional topological insulator are bilayers of bismuth. Here we report scanning tunnelling microscopy experiments on bulk Bi crystals that show that a subset of the predicted Bi-bilayers’ edge states are decoupled from the states of the substrate and provide direct spectroscopic evidence of their one-dimensional nature. Moreover, by visualizing the quantum interference of edge-mode quasi-particles in confined geometries, we demonstrate their remarkable coherent propagation along the edge with scattering properties consistent with strong suppression of backscattering as predicted for the propagating topological edge states.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout





Similar content being viewed by others
Change history
13 August 2014
In the version of this Article originally published, the name of one of the authors contained a typographical error and should have read B. Andrei Bernevig. This error has now been corrected in all versions of the Article.
References
Kane, C. L. & Mele, E. J. Quantum spin Hall effect in graphene. Phys. Rev. Lett. 95, 226801 (2005).
Kane, C. L. & Mele, E. J. Z2 topological order and the quantum spin Hall effect. Phys. Rev. Lett. 95, 146802 (2005).
Bernevig, B. A. & Zhang, S-C. Quantum spin Hall effect. Phys. Rev. Lett. 96, 106802 (2006).
Murakami, S. Quantum spin Hall effect and enhanced magnetic response by spin–orbit coupling. Phys. Rev. Lett. 97, 236805 (2006).
Hasan, M. Z. & Kane, C. L. Colloquium: Topological insulators. Rev. Mod. Phys. 82, 3045–3067 (2010).
Bernevig, B. A., Hughes, T. L. & Zhang, S-C. Quantum spin Hall effect and topological phase transition in HgTe quantum wells. Science 314, 1757–1761 (2006).
Fu, L., Kane, C. & Mele, E. Topological insulators in three dimensions. Phys. Rev. Lett. 98, 106803 (2007).
Zhang, H. et al. Topological insulators in Bi2Se3, Bi2Te3 and Sb2Te3 with a single Dirac cone on the surface. Nature Phys. 5, 438–442 (2009).
Hsieh, D. et al. Observation of unconventional quantum spin textures in topological insulators. Science 323, 919–922 (2009).
Xia, Y. et al. Observation of a large-gap topological-insulator class with a single Dirac cone on the surface. Nature Phys. 5, 398–402 (2009).
Roushan, P. et al. Topological surface states protected from backscattering by chiral spin texture. Nature 460, 1106–1109 (2009).
Chen, Y. L. et al. Experimental realization of a three-dimensional topological insulator, Bi2Te3 . Science 325, 178–181 (2009).
Hanaguri, T., Igarashi, K., Kawamura, M., Takagi, H. & Sasagawa, T. Momentum-resolved Landau-level spectroscopy of Dirac surface state in Bi2Se3 . Phys. Rev. B 82, 081305 (2010).
Cheng, P. et al. Landau quantization of topological surface states in Bi2Se3 . Phys. Rev. Lett. 105, 076801 (2010).
König, M. et al. Quantum spin Hall insulator state in HgTe quantum wells. Science 318, 766–770 (2007).
Roth, A. et al. Nonlocal transport in the quantum spin Hall state. Science 325, 294–297 (2009).
Knez, I., Du, R-R. & Sullivan, G. Evidence for helical edge modes in inverted InAs/GaSb quantum wells. Phys. Rev. Lett. 107, 136603 (2011).
Nowack, K. C. et al. Imaging currents in HgTe quantum wells in the quantum spin Hall regime. Nature Mater. 12, 787–791 (2013).
Spanton, E. M. et al. Images of edge current in InAs/GaSb quantum wells. Phys. Rev. Lett. 113, 026804 (2014).
Hofmann, P. The surfaces of bismuth: Structural and electronic properties. Prog. Surf. Sci. 81, 191–245 (2006).
Wada, M., Murakami, S., Freimuth, F. & Bihlmayer, G. Localized edge states in two-dimensional topological insulators: Ultrathin Bi films. Phys. Rev. B 83, 121310 (2011).
Chen, M. et al. Molecular beam epitaxy of bilayer Bi(111) films on topological insulator Bi2Te3: A scanning tunneling microscopy study. Appl. Phys. Lett. 101, 81603 (2012).
Cottin, M. C. et al. Anisotropic scattering of surface state electrons at a point defect on Bi(111). Appl. Phys. Lett. 98, 022108 (2011).
Cottin, M. C. et al. Interplay between forward and backward scattering of spin–orbit split surface states of Bi(111). Nano Lett. 13, 2717–2722 (2013).
Yang, F. et al. Spatial and energy distribution of topological edge states in single Bi(111) bilayer. Phys. Rev. Lett. 109, 016801 (2012).
Kim, S. H. et al. Edge and interfacial states in a two-dimensional topological insulator: Bi(111) bilayer on Bi2Te2Se. Phys. Rev. B 89, 155436 (2014).
Sabater, C. et al. Topologically protected quantum transport in locally exfoliated bismuth at room temperature. Phys. Rev. Lett. 110, 176802 (2013).
Kotaka, H., Ishii, F., Saito, M., Nagao, T. & Yaginuma, S. Edge states of Bi nanoribbons on Bi substrates: First-principles density functional study. Jpn. J. Appl. Phys. 51, 025201 (2012).
Koroteev, Y. et al. Strong spin–orbit splitting on Bi surfaces. Phys. Rev. Lett. 93, 046403 (2004).
Koroteev, Y., Bihlmayer, G., Chulkov, E. & Blügel, S. First-principles investigation of structural and electronic properties of ultrathin Bi films. Phys. Rev. B 77, 045428 (2008).
Seo, J. et al. Transmission of topological surface states through surface barriers. Nature 466, 343–346 (2010).
Crommie, M. F., Lutz, C. P. & Eigler, D. M. Imaging standing waves in a two-dimensional electron gas. Nature 363, 524–527 (1993).
Ast, C. & Höchst, H. Fermi surface of Bi(111) measured by photoemission spectroscopy. Phys. Rev. Lett. 87, 177602 (2001).
Narayan, A., Rungger, I. & Sanvito, S. Topological surface states scattering in antimony. Phys. Rev. B 86, 201402 (2012).
Chuang, F-C. et al. Tunable topological electronic structures in Sb(111) bilayers: A first-principles study. Appl. Phys. Lett. 102, 022424 (2013).
Liu, Z. et al. Stable nontrivial Z2 topology in ultrathin Bi (111) films: A first-principles study. Phys. Rev. Lett. 107, 136805 (2011).
Fu, L. & Kane, C. Topological insulators with inversion symmetry. Phys. Rev. B 76, 045302 (2007).
Teo, J., Fu, L. & Kane, C. Surface states and topological invariants in three-dimensional topological insulators: Application to Bi1−xSbx . Phys. Rev. B 78, 045426 (2008).
Ringel, Z., Kraus, Y. E. & Stern, A. Strong side of weak topological insulators. Phys. Rev. B 86, 045102 (2012).
Qi, X-L., Hughes, T. L. & Zhang, S-C. Topological field theory of time-reversal invariant insulators. Phys. Rev. B 78, 195424 (2008).
Liu, Q., Liu, C-X., Xu, C., Qi, X-L. & Zhang, S-C. Magnetic impurities on the surface of a topological insulator. Phys. Rev. Lett. 102, 156603 (2009).
Beidenkopf, H. et al. Spatial fluctuations of helical Dirac fermions on the surface of topological insulators. Nature Phys. 7, 939–943 (2011).
Delplace, P., Li, J. & Büttiker, M. Magnetic-field-induced localization in 2D topological insulators. Phys. Rev. Lett. 109, 246803 (2012).
Cheianov, V. & Glazman, L. I. Mesoscopic fluctuations of conductance of a helical edge contaminated by magnetic impurities. Phys. Rev. Lett. 110, 206803 (2013).
Li, X., Liu, H., Jiang, H., Wang, F. & Feng, J. Tuning topological edge states of Bi(111) bilayer film by edge adsorption. Nano Lett. 14, 2879–2883 (2014).
Fu, L. & Kane, C. Superconducting proximity effect and Majorana fermions at the surface of a topological insulator. Phys. Rev. Lett. 100, 1–4 (2008).
Acknowledgements
The work at Princeton and the Princeton Nanoscale Microscopy Laboratory was supported by the ARO MURI program W911NF-12-1-0461, DARPA-SPWAR Meso program N6601-11-1-4110, NSF-DMR1104612, NSF CAREER DMR-095242, ONR- N00014-11-1-0635, and NSF-MRSEC NSF-DMR0819860 programs. S.N-P. acknowledges support from the European Community through a Marie Curie fellowship (IOF 302937). The authors would like to thank F. Freimuth for providing the results of ab initio calculations and J. Seo and X. Dai for insightful discussions.
Author information
Authors and Affiliations
Contributions
I.K.D., S.J., S.N-P. and A.Y. designed and carried out the STM measurements and their analysis on samples synthesized by H.J. and R.J.C. A.A., I.K.D. and B.B. performed model calculations and related analysis. All authors contributed to the writing of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Information (PDF 1250 kb)
Rights and permissions
About this article
Cite this article
Drozdov, I., Alexandradinata, A., Jeon, S. et al. One-dimensional topological edge states of bismuth bilayers. Nature Phys 10, 664–669 (2014). https://doi.org/10.1038/nphys3048
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys3048
This article is cited by
-
High-field immiscibility of electrons belonging to adjacent twinned bismuth crystals
npj Quantum Materials (2024)
-
A hybrid topological quantum state in an elemental solid
Nature (2024)
-
Long-lived Andreev states as evidence for protected hinge modes in a bismuth nanoring Josephson junction
Nature Physics (2023)
-
Spin-charge separation and quantum spin Hall effect of \(\beta\)-bismuthene
Scientific Reports (2023)
-
Topological current divider in a Chern insulator junction
Nature Communications (2022)