Main

Physical systems with long-range interactions pose a difficult challenge to both theory and experiment and their understanding is considered an open problem, which has attracted much effort in recent years9. Long-range hydrodynamic interactions arise in particle-laden fluids, as the motion of particles relative to the surrounding fluid induces a slowly decaying perturbation of the flow field. When the suspension is enclosed in an effective two-dimensional (2D) geometry, such as in confined suspensions11,12, electrophoresis in capillaries13, protein diffusion in membranes14, and microfluidic droplets 15,16, the hydrodynamic perturbations take the form of long-range dipoles. Such dipolar systems, where the exponent of the spatial decay of the interaction equals the dimension, are known to be marginally strong and have therefore attracted special interest9. The marginal nature arises from the logarithmic divergence of the interaction with the system size, which leads to intriguing phenomena such as shape dependence, similar to that of dielectrics or magnetic dipoles17.

Recently, the collective dynamics of microfluidic droplets has generated a growing interest both as a model system for non-equilibrium dynamics and owing to their practical applications16,18,19,20,21,22,23,24,25. Here we generated a highly dynamic and disordered medium with thousands of uniform water-in-oil droplets flowing in a quasi-2D microfluidic channel of width W = 500 μm and height h = 10 μm. The droplets are shaped as discs of uniform radius in the range R = 7–11 μm (Fig. 1a). They are in contact with the horizontal floor and ceiling and deform the laminar streamlines of the carrier oil while being dragged at a mean velocity of ud = 100–200 μm s−1 that is roughly four times slower than the oil velocity (Fig. 1b,c). The system is driven far from equilibrium by the imposed flow and operates at a low Reynolds number of R e∼10−4, where viscosity dominates inertial effects. Each droplet induces a hydrodynamic dipole leading to interactions between the droplets16. The dipole is proportional to the velocity difference of oil and droplet, and is aligned with the droplet velocity. Droplet clusters constantly form and break apart erratically, and individual droplets exhibit random, diffusive-like motion due to their interactions with the other droplets20. Overall, this highly disordered system exhibits large velocity and density fluctuations that have little to do with thermal energy, consistent with a Peclet number of P e∼107.

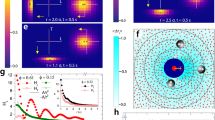
Figure 1: The microfluidic 2D droplet ensemble and velocity fluctuations.
figure 1

a, The droplets were generated at a T-junction of water and oil streams and injected at constant rate into a channel. b, The droplet geometry is disc-shaped, confined between the floor and the ceiling. The difference between the velocities of the droplet and the surrounding oil (black) induces a dipolar perturbation (red). c, Image of water droplets carried by oil, dispersed with fluorescent beads that moved during camera exposure and highlighted its flow lines (brightness inverted). Red lines show the droplet positions in time. d,e, Images show ensemble with ρ0 = 0.18. Lines drawn from the centre of each droplet are proportional to δu, its velocity relative to the mean (that is, the fluctuation of the dipoles around their mean). d, Red δ ux>0. Blue δ ux<0. e, Yellow δ uy>0. Purple δ uy<0. The rectangular frames highlight the angles along which the colours are typically uniform or mixed, corresponding to positive and negative correlations.

Full size image

We tracked the trajectories of the droplets for about 100 s in a reference frame moving at the mean droplet velocity, and measured the velocity fluctuation of each droplet, , where u(t) is the droplet’s velocity at time t and is the mean flow direction downstream the channel. The droplets’ mean area fraction ρ0 was varied in the range of 0.07–0.63 between measurements and remained roughly constant during each one. The snapshot in Fig. 1d,e shows distinctive patterns of δu for ρ0 = 0.18 with stripes of oriented droplet velocities. These structures demonstrate collective motion with spatial velocity correlations, corresponding to orientational ordering of the hydrodynamic dipoles that are aligned with the velocities. We define the spatial velocity correlation of the measured δ ux between two points separated by a vector r = (r,θ):

Here, δ ux is the x component of δu and averaging is performed over the position r′ and time t, such that both r′ and r′+r fall within the central half of the channel to avoid boundary effects. A similar definition applies for δ uy. Despite the disordered dynamics, the velocity correlations show remarkable long-range order and symmetry (Fig. 2a–e). Both Cx and Cy persist over long distances of r = 15–20R before falling below noise level. At large distances, r = 5–20R, the correlation exhibits the following hallmarks: decay similar to a power law of r−2 (Fig. 2c and Supplementary Fig. 1 for all of the measured densities); anti-symmetry: Cy(r,θ)≈−Cx (r,θ) (Fig. 2d,e); four-fold angular symmetry, ∼cos(4θ), with positive maxima reflecting a tendency for joint motion in a particular direction, and negative minima that indicate relative motion in opposite directions, that is dilation, contraction or rotation.

Figure 2: Velocity correlations.
figure 2

a,b, Cx and Cy versus x and y at ρ0 = 0.18. c, Cx and Cy versus r for a vertical droplet pair (θ = 90°). The solid line is an r−2 curve. d,e, Cx,y versus θ at r = 8R. Conditional correlations Cx,y± reveal structures and dynamics in the droplet ensemble: Cx,y+ includes only the droplets with δ ux,y(r′,t)>0, and Cx,y− that is constrained to δ ux,y(r′,t)<0. The peak at Cx+(θ = 90) corresponds to fast droplets (δ ux>0), aligned perpendicular to the flow, whereas the peak at Cx−(θ = 0°) indicates slow droplets aligned along the flow. The peaks of Cy+ and Cy− show that droplets aligned along diagonals at θ≃45° have correlated downwards velocity (δ uy<0), whereas those aligned along θ≃−45° diagonals move upwards (δ uy>0). f, Velocity variance 〈δ ux,y2〉. g, Theoretical Cx,y given by equation (4) and Supplementary Eq. 17. h, Velocity fluctuations δ ux (purple) and δ uy (violet) of two test droplets typically have parallel or opposite signs owing to their interactions with a third droplet (light blue), depending on θ. Error bars represent uncertainty due to temporal fluctuations of the measured correlations.

Full size image

To reveal which droplets contribute to the correlations we computed the conditional correlation function defined similarly to equation (1), but limited to positive or negative fluctuations in x and y directions (details in Fig. 2d,e and Supplementary Information). The peaks of the conditional correlations correspond to the characteristic stripy patterns of the orientational order shown in Fig. 1d,e. The correlations manifest the collective dynamics of the droplets: its positive peaks reveal distinct structures and, at the same time, its negative peaks show how these structures are unstable, dynamically breaking and reforming. Consider, for example, a droplet pair with θ = 90°: on average, the two droplets move fast together along x (Cx+(θ = 90°)>0) and simultaneously move in opposite directions along y (Cy±(θ = 90°)<0), which either increases or decreases the distance between them. A pair of droplets separated by θ≃45° tend to move together downwards along y and simultaneously move in opposite directions along x, which changes θ. Finally, we measured the variance of the velocity, 〈δ ux2〉 = Cx(r = 0) and 〈δ uy2〉 = Cy(0). The variances, in units of ud2, increase with the area fraction ρ0, until they peak at ρ0∼0.25, and then attenuate at higher density (Fig. 2f).

To explain the orientational order manifested by the velocity correlations, we consider the interactions in the 2D ensemble of hydrodynamic dipoles20. In the thin channel, the oil velocity can be decoupled into Poiseuille flow along the z axis perpendicular to the plane, and a 2D potential Stokes flow in the x y plane (Fig. 1b). Far from the confining sidewall boundaries, the disturbance of a single droplet to the oil velocity is the gradient of the 2D dipole potential, Φ(r) = Δu · ϕ(r) with ϕ(r) = R2cos(θ)/r and Δu = uoil−u is the difference between the unperturbed oil velocity at the droplet position (assuming the droplet is absent) and the droplet velocity. Two opposing forces act on each droplet: a drag by the surrounding oil and a friction force by the solid boundaries at the channel floor and ceiling. As inertia is negligible, the forces are balanced, resulting in a linear relation u = K uoil, where the coupling constant K∼0.25 depends only on geometry and material properties 8,16 (Supplementary Information).

Owing to the linearity of Stokes flow, in an ensemble with inter-droplet distances much larger than R, the oil velocity is well approximated by a superposition of the droplet dipoles and the uniform oil flow, . The equation of motion of a droplet at r is u(r) = K uoil(r), where uoil(r) is the velocity of oil including the perturbations of all the other droplets16. We represent corrections to this far-field approximation by an effective velocity scale U for the interaction strength that will be determined experimentally (see Supplementary Information):

The correlation between the velocity fluctuations of two droplets at a distance r is found from equations (1) and (2) to be the averaged sum over all dipole pairs in the ensemble:

and similarly for Cy. The summation over i and j represents the interaction of the droplet pair with all of the other droplets in the ensemble. Equation (3) can be separated into two parts: a single-droplet contribution CxI(r), including all terms with i = j, that accounts for the velocity change of the two test droplets due to their interactions with a third droplet at ri, and a dual-droplet part, CxII(r) including all interactions of the pair with two different droplets i≠j.

We first consider the simple case of a randomly positioned ensemble: if the positions of the ith and jth droplets are independent, then by symmetry the average over the product of their dipolar fields vanishes, CxII(r) = 0, and hence Cx = CxI. The time average in equation (3) can therefore be replaced by an integral over a uniform density distribution, n0 = ρ0/πR2, that for r≳8R yields (Supplementary Fig. 2 for the full solution):

In addition, Cy(r) = −Cx(r). Equation (4) captures the three salient features of the measured velocity correlations: the r−2 power law, the x y anti-symmetry, and the cos(4θ) angular dependence. Interestingly, the velocity correlation is given by the auto-correlation of , which implies that the effect of an entire random ensemble on the test-pair is equivalent to the average effect of a third droplet. To elucidate this effect, Fig. 2h shows droplet pairs (grey) at angles θ = 0°,45°,90° and a third droplet (light-blue) between each pair. When θ = 0°,90° the third droplet’s dipole has both a positive contribution to Cx, because it pushes the pair to the same direction along x, and at the same time, a negative contribution to Cy, because it pushes the pair in opposite directions along y. When θ = 45°, it has a positive contribution to Cy and a negative contribution to Cx.

Remarkably, the velocity correlations originate from the interactions of the pair with the entire ensemble and not from the interaction within the pair. The latter is not included in equation (4) and decays as , much faster than the ∼r−2 decay measured at large distances. Moreover, the interaction within the pair cannot explain negative correlations, because the forces that any two droplets apply on each other are identical owing to the symmetry of the dipole field, .

The predicted peaks of the correlations at θ = ±45° are observed for ρ0<0.6 at an average angle of ±41°±2.5° for Cx, and ±38°±2° for Cy (Fig. 2d,e). In addition, the peaks at θ = 90° and θ = 0° differ in amplitude, in contrast to the theoretical cos(4θ). These differences may largely be attributed to dependencies between droplet positions due to clustering and density waves20,24 that were neglected. To refine equation (4) we consider excluded-volume effects in the low-density limit, ρ0≪1, and find that the dual-droplet term CxII no longer vanishes: CxII(r) = −4ρ0CxI(r) for r≫R, whereas CxI is unchanged, resulting in, Cx(r) = (1−4ρ0)CxI(r) (see Supplementary Information). Thus, excluded volume does not alter the spatial structure of the velocity correlations but introduces a density-dependent inhibition to the correlation amplitude, 〈δ ux2〉≡Cx(r = 0), which is proportional to ρ02 because it depends on the number of droplet pairs.

The inhibitory effect due to excluded volume reflects a competition between two density-dependent effects that determine the observed peak of the velocity variance 〈δ ux2〉 = CxI(r = 0)+CxII(r = 0) (Fig. 2f). Here, , which is positive and . A simple toy-model provides intuition why the second term is always negative owing to excluded-volume effects (Fig. 3a). Consider two droplets that can be positioned at the four corners of a square surrounding a test droplet (black). Then, CxII(0) is the product of the two fields at the test-droplet’s location, averaged over all of the possible configurations. From symmetry it is enough to consider 3 out of the 12 possible configurations, where one droplet is fixed at the bottom left corner and the other can occupy any of the other three spots. In two of these configurations, the dipole fields have opposite directions at the test droplet’s position, whereas only in one configuration their directions are aligned. As a result, their average product is negative, hence CxII(0)<0. Without the effect of excluded volume, one would consider a fourth configuration, in which both droplets occupy the same spot, forming a second configuration with aligned fields that nullifies the average product.

Figure 3: Velocity variance determined by competition of single- and dual-droplet effects.
figure 3

a, Toy-model: a test droplet (black) surrounded by four available slots (dashed circles) that are occupied by two droplets. As a result of excluded volume, in two out of three configurations, the dipole fields at the test droplet are anti-parallel setting CyII(0) negative. b, The pair-distribution function, n(2)(r), the probability to find a droplet r away from a reference droplet is measured at different ρ0, and plotted for , peaks at r≃2R, indicating high probability to find droplets in contact owing to clustering. Broken curves are n(2)(r) of randomly placed droplets in silico. c, Cx,yI(0) is positive, whereas Cx,yII(0) is negative. Both increase in magnitude with ρ0. Blue curves are Cx,yI(0) and Cx,yII(0) calculated in silico. d, The sum [CyI(0)+CyII(0)]/U2 (right triangle) is similar to Cy(0)/ud2 (open circle). Blue curves are in silico CyI(0)+CyII(0) (dots) and Cy(0) (solid line), which agree throughout the ρ0 range. Error bars represent uncertainty due to temporal fluctuations of the measured correlations.

Full size image

To compare the theoretical value of CxI(0)+CxII(0) to the measured velocity variance 〈δ ux2〉 (Fig. 2f), we measured the spatial pair- and triplet-distribution functions that describe the non-random distribution of distances between droplets (Fig. 3b and Supplementary Fig. 3). These functions are used as weights in averaging over the ensemble positions in calculating CxI(0) and CxII(0) (see Supplementary Information). Both functions peak at distances of touching droplets but decay to a constant value for larger distances. In agreement with theory, Fig. 3c shows that CxI(0) is positive whereas CxII(0) is negative, both increasing in magnitude with density ρ0, and have similar values for y. The computed sum CyI(0)+CyII(0) in units of U2 fits well to the measured Cy(0) (Fig. 3d), which suggests that the interaction velocity scale U is U≈ud throughout the measured range of ρ0 (Cx(0) is discussed in the Supplementary Information). The theoretical far-field value, U = (1−K)ud≈ud, matches our experimental result.

Finally, we computed the velocity correlations in silico by randomly placing droplets, considering their mutually excluded volume, and evaluating the inter-droplet dipolar forces (see Supplementary Information). In agreement with theory, the numerical calculation shows a cos 4θ symmetry and r−2 decay of the correlations (Supplementary Fig. 4), as well as a peak at ρ0 = 0.34 in the velocity variances (Fig. 3d).

Similarly to a nematic liquid crystal, the hydrodynamic dipoles exhibit partial order: positional correlations decay fast owing to spatial disorder, whereas the orientational degrees-of-freedom remain correlated over long-range. As in the 2D droplet ensembles reported here, also in gravitational sedimentation of particles in 2D and 3D, the velocity variance decreases at high densities2,12,26. However, so far this generic decrease has lacked a first-principles theoretical explanation. In Brownian quasi-2D suspensions of particles in equilibrium, the dipoles are randomly oriented and there is no symmetry-breaking direction. Hence, at large distances velocity correlations are determined only by two-body interactions11. Future studies may reveal how the velocity correlations are coupled to dynamic clustering, which has an important role in setting the fluctuations. We expect our results to have applications in the design of active and self-propelled systems27,28 as well as in droplet-based microfluidic devices used in biology and chemistry29,30.

Methods

The channel was made of polydimethylsiloxane elastomer casted on a mould, which was prepared by lithography. After curing at 80 °C for 1 h, the channel was detached from the mould and irreversibly attached on a polydimethylsiloxane-coated glass slide16,20. The carrier fluid was light mineral oil (Sigma, M5904, viscosity ηoil = 30 mPa, density ρ0 = 0.84 g ml−1) with 2% (w/w) Span-80 surfactant (Sigma). The dispersed fluid was distilled water. The experiment was imaged by a PCO.Sensicam (PCO) camera for about 100 s at 21 frames s−1. We used a precise tracking algorithm (the Moses–Abadi algorithm) 8 implemented in Matlab (Mathworks) to analyse the images acquired in the experiment. Each droplet’s centre position was tracked and followed between subsequent images to construct its trajectory. The droplet velocities were computed by five-point time derivatives of their x and y positions. To compute the velocity correlations Cx(r) we computed the average product of the velocity fluctuations δ ux of all droplet couples within the channel’s central half that were separated by r = (r,θ). The velocity fluctuations were defined as the difference between the droplets’ individual velocities and the locally measured mean velocity. Owing to the spatial and temporal fluctuations of the mean droplet velocity, it was measured separately for each droplet pair. The mean velocity was defined as the average velocity of droplets within a rectangle of length W along x (centred at the mean x position of the droplet pair) and width W/2 along y (centred at the middle of the channel).