Abstract
The interplay of magnetic and charge fluctuations can lead to quantum phases with exceptional electronic properties. A case in point is magnetically-driven superconductivity1,2, where magnetic correlations fundamentally affect the underlying symmetry and generate new physical properties. The superconducting wavefunction in most known magnetic superconductors does not break translational symmetry. However, it has been predicted that modulated triplet p-wave superconductivity occurs in singlet d-wave superconductors with spin-density-wave (SDW) order3,4. Here we report evidence for the presence of a spatially inhomogeneous p-wave Cooper pair-density wave in CeCoIn5. We show that the SDW domains can be switched completely by a tiny change of the magnetic field direction, which is naturally explained by the presence of triplet superconductivity. Further, the Q-phase emerges in a common magneto-superconducting quantum critical point. The Q-phase of CeCoIn5 thus represents an example where spatially modulated superconductivity is associated with SDW order.
Similar content being viewed by others
Main
Superconductivity emerges in solids when electrons form Cooper pairs at low temperatures and condense in a macroscopically coherent quantum state, leading to zero-resistance and diamagnetism. For most phonon-mediated superconductors, the symmetry of the superconducting gap function is an isotropic singlet s-wave that does not break the symmetries of the underlying lattice. Unconventional superconductors5,6 adopt more complex wavefunctions: singlet d-wave in cuprates, extended s-wave for the pnictides and p-wave in ruthenates7. Although co-existing wavefunctions are theoretically possible, most superconductors are adequately described by just a single wavefunction. Here we provide evidence that p-wave superconductivity emerges in a d-wave superconductor and couples to a SDW—forming a unique quantum phase with a spatially inhomogeneous superconducting Cooper pair-density wave (PDW).
The stoichiometric heavy-fermion superconductorCeCoIn5 serves as a model material for studies of -wave superconductivity8,9. It shares many properties with the cuprate superconductors, such as the zero-field superconducting wavefunction10,11,12 symmetry, a quasi-two-dimensional Fermi surface13 and a spin resonance in the superconducting state14. Superconductivity emerges below Tc(0) = 2.3 K and is Pauli-limited. The superconducting phase transition becomes first-order15 close to Hc2(0), where SDW order has been observed that only exists in the Q-phase situated inside the superconducting phase16,17,18. The SDW propagation is pinned along the -line nodes, where low-energy quasiparticles allow for electron nesting17 (Fig. 1a).
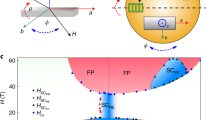
a, -superconducting wavefunction and external magnetic field H along the nodal  and fully gapped [100] direction, where identical SDW order was detected16,17. b, The nature of the lower Q-phase boundary for
and fully gapped [100] direction, where identical SDW order was detected16,17. b, The nature of the lower Q-phase boundary for  (blue diamonds) and [100] (red circles) was investigated by probing the magnetic Bragg peak intensity as a function of H at T = 40 mK and 80 mK, respectively. Magnetism appears in a continuous second-order phase transition. Thus, a magnetically driven quantum critical point is located inside the superconducting phase at HQ(0). The onset field μ0HQ≈9.8 T, coincides with the field strength H0, where the superconducting transition becomes first-order and anisotropic (see inset). Solid blue and red lines depict linear fits to the intensity
(blue diamonds) and [100] (red circles) was investigated by probing the magnetic Bragg peak intensity as a function of H at T = 40 mK and 80 mK, respectively. Magnetism appears in a continuous second-order phase transition. Thus, a magnetically driven quantum critical point is located inside the superconducting phase at HQ(0). The onset field μ0HQ≈9.8 T, coincides with the field strength H0, where the superconducting transition becomes first-order and anisotropic (see inset). Solid blue and red lines depict linear fits to the intensity  and I100, respectively. Blue, red and grey dashed lines are guides to the eye for
and I100, respectively. Blue, red and grey dashed lines are guides to the eye for  , Hc2,100 and the background, respectively. Error bars correspond to 1 standard deviation (s.d.).
, Hc2,100 and the background, respectively. Error bars correspond to 1 standard deviation (s.d.).
In some microscopic theories addressing the nature of the Q-phase, the formation of a spatially modulated Fulde–Ferrell–Larkin–Ovchinnikov (FFLO) state plays a central role19. Other theoretical approaches emphasize SDW nesting20,21. Phenomenologically it has been shown3,16 that SDW order in a d-wave superconductor always couples to a PDW of mixed singlet/triplet nature. The precise symmetry properties of possible coupling terms have been presented by Agterberg et al. 4:


where Δ0, MQz and Δ−Q represent the , SDW and PDW order parameter, respectively. The finite-momentum (−Q) triplet PDW component is required to conserve momentum (translational symmetry). An FFLO state would be only weakly modulated, qFFLO<Q, and so a phenomenological interaction coupling to FFLO order in the presence of SDW would require additional, higher-order coupling terms.
We searched for evidence of coupling terms V 1 or V 2 through an investigation of the lower Q-phase boundary. Figure 1b shows a high-statistics measurement of the H-dependence of the magnetic Bragg peak intensity for H∥[100] and  . The onset of the magnetic scattering occurs at a continuous phase transition at μ0HQ(0)≈9.8 T, is independent of the field direction in the basal plane and grows linearly with field. It corresponds also to the field strength H0≈HQ(0), where the superconducting transition becomes first-order15. The magnetic neutron intensity is proportional to the square of the magnetic moment I
. The onset of the magnetic scattering occurs at a continuous phase transition at μ0HQ(0)≈9.8 T, is independent of the field direction in the basal plane and grows linearly with field. It corresponds also to the field strength H0≈HQ(0), where the superconducting transition becomes first-order15. The magnetic neutron intensity is proportional to the square of the magnetic moment I M2, that is, the measured SDW order parameter grows as M
M2, that is, the measured SDW order parameter grows as M (H/H0−1)β with a critical exponent β≈0.5—as expected for a quantum phase transition. Our data excludes an additional phase22 adjacent to the Q-phase.
(H/H0−1)β with a critical exponent β≈0.5—as expected for a quantum phase transition. Our data excludes an additional phase22 adjacent to the Q-phase.
Microscopic theories that rely on nesting and an increased density of states naturally lead to the coexistence of Q-domains or the emergence of so-called double Q-phases, particularly for H∥[100]. The two possible SDW domains Qh and Qv, associated with Q = (q,±q,0.5), are shown in Fig. 2a–c. For fields  , we find all four horizontal Bragg peaks associated with Qh, one of which is shown in Fig. 2d. However, no peaks belonging to the Qv-domain, as for example (0.44,−0.44,0.50), were detected (Fig. 2e), showing that only one of the two SDW domains is populated for fields along the nodal direction. Even for a field along the anti-nodal direction (H∥[100]), where both Q-domains are identical by symmetry, we find a mono-domain state (see Supplementary Discussion). The angle ψ between H and [100] was smaller than 0.2°. This is evidence against the available microscopic theories and suggests the presence of an additional order parameter such as a PDW.
, we find all four horizontal Bragg peaks associated with Qh, one of which is shown in Fig. 2d. However, no peaks belonging to the Qv-domain, as for example (0.44,−0.44,0.50), were detected (Fig. 2e), showing that only one of the two SDW domains is populated for fields along the nodal direction. Even for a field along the anti-nodal direction (H∥[100]), where both Q-domains are identical by symmetry, we find a mono-domain state (see Supplementary Discussion). The angle ψ between H and [100] was smaller than 0.2°. This is evidence against the available microscopic theories and suggests the presence of an additional order parameter such as a PDW.
a,b, SDW domains in real space: magnetic moments M∥[001] are modulated perpendicular to the orthogonal propagation vectors Qh and Qv. c, Corresponding magnetic Bragg positions form an eightfold star of Q-vectors in reciprocal space. The orange subset of equivalent positions Qh = (q,q,0.5) lies completely in the horizontal scattering plane, whereas the grey Qv = (q,−q,0.5) domain has vertical components  . d, Diffracted intensity of the Qh-domain at T = 50 mK and μ0H = 11.2 T for
. d, Diffracted intensity of the Qh-domain at T = 50 mK and μ0H = 11.2 T for  (red circles). Magnetic scattering is absent in the normal state (μ0H = 12.0 T, blue diamonds). The scan is shown in reciprocal lattice units (r.l.u.). e, Background-subtracted diffracted intensity I11.2 T−12.0 T (red circles) of a rotation ω-scan at (0.44, −0.44, 0.5) for
(red circles). Magnetic scattering is absent in the normal state (μ0H = 12.0 T, blue diamonds). The scan is shown in reciprocal lattice units (r.l.u.). e, Background-subtracted diffracted intensity I11.2 T−12.0 T (red circles) of a rotation ω-scan at (0.44, −0.44, 0.5) for  at T = 50 mK, with a moving average of nearest neighbours for the normal state data, indicates an unpopulated Qv-domain. Lines depict Gaussian fits to the data. Error bars correspond to 1 s.d.
at T = 50 mK, with a moving average of nearest neighbours for the normal state data, indicates an unpopulated Qv-domain. Lines depict Gaussian fits to the data. Error bars correspond to 1 s.d.
The observation of only one SDW domain for H∥[100] points towards a hypersensitivity of the Q-phase with respect to H. To determine the switching field direction, we equipped the dilution refrigerator with a piezoelectric attocube sample rotator. Figure 3a shows the integrated Bragg peak intensity of the Qh- and Qv-domains as a function of the angle ψ (Fig. 3b). The domain population can be fully switched within only Δ ψ≈0.1°.
a, Integrated intensity of the Qh- (red circles) and the Qv-domain (blue diamonds), normalized to the averaged respective full population, as a function of the tilt angle ψ (see sketch b). A mono-domain population is observed for |ψ|≥0.05°, which can be macroscopically switched in a sharp transition. Thus, the magnetic field direction allows direct access and control of the complex quantum state in the Q-phase. The magneto-superconducting state was newly prepared for each field direction. c,d, Measurement of the hysteresis ψ≈0.2° of the first-order domain switch by field rotation without leaving the Q-phase. Data measuring while increasing (decreasing) the tilt angle are in red (orange) circles (c) and dark blue (light blue) diamonds (d). Lines and shaded areas are guides to the eyes. Error bars correspond to 1 s.d.
The nature of the SDW switch was further probed at (q,±q,0.5) by rotating H without leaving the Q-phase. We find a first-order domain switching with a hysteresis of only Δ ψ≈0.2° (Fig. 3c,d). This provides evidence that the two coexistent single-Q SDW domains are not in a coherent superposition (double-Q-state) for |ψ|≤0.05°, because the domain population changes hysteretically from unpopulated to populated.
The observed hypersensitivity of the Q-domain on the magnetic field direction is remarkable. A Zeeman term M · H that controls magnetic domains in other SDW materials, such as Cr or MnSi, can be excluded as the origin: the SDW ordered moments M∥ [001] are perpendicular to H for all fields in the tetragonal plane16,17. Alternatively, if the Q-phase were FFLO driven, it is possible that weakly localized magnetic moments at FFLO nodal planes19 could lead to SDW mono-domains through the difference of the horizontal and vertical SDW coherence length. However, this scenario does not easily explain the hypersensitivity of the mono-domain state around [100], which would require a fine-tuning of interactions. Similar modifications would be necessary if the Q-phase were purely nesting driven20.
A simpler scenario, where a SDW and PDW are coupled in the presence of the d-wave condensate is described by equation (1), which involves singlet/triplet mixing. The symmetry of the PDW is highly constrained: for  and Qh = (q,q,0.5) the allowed p-wave component is a linear combination of two spin-triplet pairing vector functions d1(k) = (0,0,kx−ky) (nodes along [110], Fig. 4a) and d2(k) = (kz,−kz,0) (nodal plane (h, l, 0)). As the direction of the SDW Q-vector and the nodal direction of the p-wavefunction are identical, the PDW and SDW can naturally coexist and couple. In contrast, the gap functions4 allowed by the alternate coupling in equation (2) do not produce nodes along [110], and thus compete with SDW formation.
and Qh = (q,q,0.5) the allowed p-wave component is a linear combination of two spin-triplet pairing vector functions d1(k) = (0,0,kx−ky) (nodes along [110], Fig. 4a) and d2(k) = (kz,−kz,0) (nodal plane (h, l, 0)). As the direction of the SDW Q-vector and the nodal direction of the p-wavefunction are identical, the PDW and SDW can naturally coexist and couple. In contrast, the gap functions4 allowed by the alternate coupling in equation (2) do not produce nodes along [110], and thus compete with SDW formation.
a, A phenomenological lowest-order linear coupling term of -superconductivity and incommensurate SDW order requires, as a result of momentum conservation, the appearance of an additional triplet PDW component. The constraints in the Q-phase allow only one particular triplet state, represented by a linear combination of two dumbbell-shaped p-wave gap functions. The schematic shows the d1-triplet component for  , where electron nesting of low-energy quasiparticles is only possible along the nodes perpendicular to the field direction (
, where electron nesting of low-energy quasiparticles is only possible along the nodes perpendicular to the field direction ( ). The triplet component also accounts for the hypersensitive switching of the SDW close to H∥[100]. The point symmetry of the gap functions is shown. The nodes of both the d- and p-wave superconducting gap functions are in reciprocal space. b, Representation of the local PDW gap structure along the [110] direction in real space. The Cooper pair-density wave is modulated in real space as a result of the direct coupling to the incommensurate SDW order. This produces additional nodes in real space where the amplitude of the p-wave gap function is zero.
). The triplet component also accounts for the hypersensitive switching of the SDW close to H∥[100]. The point symmetry of the gap functions is shown. The nodes of both the d- and p-wave superconducting gap functions are in reciprocal space. b, Representation of the local PDW gap structure along the [110] direction in real space. The Cooper pair-density wave is modulated in real space as a result of the direct coupling to the incommensurate SDW order. This produces additional nodes in real space where the amplitude of the p-wave gap function is zero.
Experimentally, we observe that electron nesting in the Q-phase occurs always along the -node direction that is more perpendicular to the applied field ( ). Triplet components can feature a strongly anisotropic magnetic susceptibility, as in the A-phase23 of 3He and also for d2(k). This provides a simple microscopic mechanism for the switching behaviour: H controls the p-wave line node, which simultaneously determines the direction of the SDW wave-vector. As some components of the magnetic susceptibility tensor of p-wave superconductivity do not change compared to the normal phase, there are nuclear magnetic resonance lines at the position of the normal state24. Our arguments are bolstered by a significantly enhanced spin susceptibility25 in the Q-phase, compared to the main d-wave phase, and by measurements of the quasiparticle entropy26. The switching behaviour of the SDW domains should also affect the thermal conductivity, making it anisotropic and hypersensitive to the field direction.
). Triplet components can feature a strongly anisotropic magnetic susceptibility, as in the A-phase23 of 3He and also for d2(k). This provides a simple microscopic mechanism for the switching behaviour: H controls the p-wave line node, which simultaneously determines the direction of the SDW wave-vector. As some components of the magnetic susceptibility tensor of p-wave superconductivity do not change compared to the normal phase, there are nuclear magnetic resonance lines at the position of the normal state24. Our arguments are bolstered by a significantly enhanced spin susceptibility25 in the Q-phase, compared to the main d-wave phase, and by measurements of the quasiparticle entropy26. The switching behaviour of the SDW domains should also affect the thermal conductivity, making it anisotropic and hypersensitive to the field direction.
Nuclear magnetic resonance identified low-energy quasiparticles24 whose density of states scales with a critical exponent β≈0.5, identical to that of the SDW that we observe in our present study. This suggests that the transition at HQ(0) also affects the electronic structure, and may constitute a magneto-superconducting quantum critical point involving both superconducting and magnetic degrees of freedom. This is additional evidence for the presence of a linear coupling term as described in equation (1).
Our results suggest that the quantum critical point for fields in the tetragonal plane27 near Hc2(0) is located at HQ(0) and involves both magnetic and charge degrees of freedom. It is characterized with a relatively subtle change of the electronic structure compared to what is expected in a Kondo breakdown scenario. Probably a similar scenario can also explain the quantum critical point28,29 observed for fields along the tetragonal axis, where an anisotropic violation of the Wiedemann–Franz law points towards an anisotropic destruction of the Fermi surface30.
The sharp switching of magneto-superconducting domains provides evidence for the condensation of a spatially modulated triplet PDW (Fig. 4b), which emerges spontaneously with a SDW at HQ(T). Our experiment does not allow a distinction of whether the SDW or the p-wave PDW drives the Q-phase. A non-unitary extension of the proposed d-vector representatives4 may suggest a related scenario, where SDW moments represent the ordering of ferromagnetic components of the Cooper pair-density wave.
Our experiment confirms the general prediction that an incommensurate SDW in a singlet superconductor can couple to a spatially inhomogeneous triplet PDW (ref. 3). The method showcases a new approach to study the properties of the quantum condensate in a superconductor. Finally, the observed switching of magneto-superconducting domains and the manipulation of a quantum state using magnetic fields may represent a promising approach for the encoding of quantum information in the solid state.
Methods
High-field neutron diffraction experiments were carried out on the thermal neutron two-axis diffractometer D23 at the Institut Laue-Langevin, Grenoble, France and the cold neutron triple-axis spectrometer RITA-II at the Swiss Spallation Neutron Source SINQ, Paul Scherrer Institut, Villigen, Switzerland. The same CeCoIn5 single-crystal with a mass of 155 mg was used on both instruments. Temperatures down to T = 40 mK and external magnetic fields of up to μ0H = 12.0 T were reached with vertical-field cryomagnets and dilution refrigerator inserts. D23 is equipped with a lifting-arm detector, which allows measuring a wave vector transfer with a vertical component, that is, along the magnetic-field direction. Measurements on D23 were carried out with an incident neutron wavelength of λn = 1.28 Å obtained from the (2, 0, 0) Bragg reflection of a flat Cu monochromator. λn = 4.04 Å from the (0, 0, 2) reflection of a vertically focusing pyrolitic graphite monochromator was used on RITA-II. There, a beryllium filter in front of the nine-bladed pyrolitic graphite multi-analyser minimized contributions of higher order neutrons. Data shown in Fig. 1 were recorded by keeping the diffractometer at the Bragg position, whilst ramping H. This is justified, because the peak position moves much less than its resolution. q-scans are depicted in (h, k, l) reciprocal lattice units (r.l.u.). Measurements with a rotating field direction were carried out on the instrument D23 by using a non-magnetic piezoelectric sample rotator (type ANGt50 from attocube systems AG) inside the dilution refrigerator. The field direction was measured using a built-on Hall probe as well as through the vertical tilt of (0, k, l) nuclear Bragg peaks. An additional thermometer located next to the sample allowed an accurate measurement of the sample temperature (see Supplementary Methods).
References
Mathur, N. D. et al. Magnetically mediated superconductivity in heavy fermion compounds. Nature 394, 39–43 (1998).
Monthoux, P., Pines, D. & Lonzarich, G. G. Superconductivity without phonons. Nature 450, 1177–1183 (2007).
Aperis, A., Varelogiannis, G. & Littlewood, P. B. Magnetic-field-induced pattern of coexisting condensates in the superconducting state of CeCoIn5 . Phys. Rev. Lett. 104, 216403 (2010).
Agterberg, D. F., Sigrist, M. & Tsunetsugu, H. Order parameter and vortices in the superconducting Q phase of CeCoIn5 . Phys. Rev. Lett. 102, 207004 (2009).
Norman, M. R. The challenge of unconventional superconductivity. Science 332, 196–200 (2011).
Sigrist, M. & Ueda, K. Phenomenological theory of unconventional superconductivity. Rev. Mod. Phys. 63, 239–311 (1991).
Mackenzie, A. P. & Maeno, Y. The superconductivity of Sr2RuO4 and the physics of spin-triplet pairing. Rev. Mod. Phys. 75, 657–712 (2003).
Petrovic, C. et al. Heavy-fermion superconductivity in CeCoIn5 at 2.3 K. J. Phys. Condens. Matter 13, L337–L342 (2001).
Thompson, J. D. & Fisk, Z. Progress in heavy-fermion superconductivity: Ce115 and related materials. J. Phys. Soc. Jpn 81, 011002 (2012).
Movshovich, R. et al. Unconventional superconductivity in CeIrIn5 and CeCoIn5: Specific heat and thermal conductivity studies. Phys. Rev. Lett. 86, 5152–5155 (2001).
Izawa, K. et al. Angular position of nodes in the superconducting gap of quasi-2D heavy-fermion superconductor CeCoIn5 . Phys. Rev. Lett. 87, 057002 (2001).
Curro, N. J. et al. Anomalous NMR magnetic shifts in CeCoIn5 . Phys. Rev. B 64, 180514(R) (2001).
Settai, R. et al. Quasi-two-dimensional Fermi surfaces and the de Haas-van Alphen oscillation in both the normal and the superconducting mixed states of CeCoIn5 . J. Phys. Condens. Matter 13, L627–L634 (2001).
Stock, C., Brohom, C., Hudis, J., Kang, H. J. & Petrovic, C. Spin resonance in the d-wave superconductor CeCoIn5 . Phys. Rev. Lett. 100, 087001 (2008).
Bianchi, A., Movshovich, R., Capan, C., Pagliuso, P. G. & Sarrao, J. L. Possible Fulde–Ferrell–Larkin–Ovchinnikov state in CeCoIn5 . Phys. Rev. Lett. 91, 187004 (2003).
Kenzelmann, M. et al. Coupled superconducting and magnetic order in CeCoIn5 . Science 312, 1652–1654 (2008).
Kenzelmann, M. et al. Evidence for a magnetically driven superconducting Q phase of CeCoIn5 . Phys. Rev. Lett. 104, 127001 (2010).
Young, B.-L. et al. Microscopic evidence for field-induced magnetism in CeCoIn5 . Phys. Rev. Lett. 98, 036402 (2007).
Yanase, Y. & Sigrist, M. Ginzburg–Landau analysis for the antiferromagnetic order in the Fulde–Ferrell–Larkin–Ovchinnikov superconductor. J. Phys. Soc. Jpn 80, 094702 (2011).
Suzuki, K. M., Ichioka, M. & Machida, K. Theory of an inherent spin-density-wave instability due to vortices in superconductors with strong Pauli effects. Phys. Rev. B 83, 140503(R) (2011).
Kato, Y., Batista, C. D. & Vekhter, I. Antiferromagnetic order in Pauli-limited unconventional superconductors. Phys. Rev. Lett. 107, 096401 (2011).
Koutroulakis, G. et al. Field evolution of coexisting superconducting and magnetic orders in CeCoIn5 . Phys. Rev. Lett. 104, 087001 (2010).
Leggett, A. J. A theoretical description of the new phases of liquid 3He. Rev. Mod. Phys. 47, 331–414 (1975).
Kumagai, K., Shishido, H., Shibauchi, T. & Matsuda, Y. Evolution of paramagnetic quasiparticle excitations emerged in the high-field superconducting phase of CeCoIn5 . Phys. Rev. Lett. 106, 137004 (2011).
Mitrović, V. F. et al. Observation of spin susceptibility enhancement in the possible Fulde–Ferrell–Larkin–Ovchinnikov state of CeCoIn5 . Phys. Rev. Lett. 97, 117002 (2006).
Tokiwa, Y., Bauer, E. D. & Gegenwart, P. Quasiparticle entropy in the high-field superconducting phase of CeCoIn5 . Phys. Rev. Lett. 109, 116402 (2012).
Ronning, F. et al. Field-tuned quantum critical point in CeCoIn5 near the superconducting upper critical field. Phys. Rev. B 71, 104528 (2005).
Bianchi, A., Movshovich, R., Vekther, I., Pagliuso, P. G. & Sarrao, J. L. Avoided antiferromagnetic order and quantum critical point in CeCoIn5 . Phys. Rev. Lett. 91, 257001 (2003).
Paglione, J. et al. Field-Induced quantum critical point in CeCoIn5 . Phys. Rev. Lett. 91, 246405 (2003).
Tanatar, M. A., Paglione, J., Petrovic, C. & Taillefer, L. Anisotropic violation of the Wiedemann–Franz law at a quantum critical point. Science 316, 1320–1322 (2007).
Acknowledgements
This work is based on neutron scattering experiments performed at the Institut Laue-Langevin, Grenoble, France and the Swiss Spallation Neutron Source SINQ, Paul Scherrer Institute, Villigen, Switzerland. We thank P. Fouilloux and M. Zolliker for technical assistance. Discussions with M. Sigrist as well as C. Batista, P. Coleman, K. Machida, K. Kumagai and J. S. White are acknowledged. This work was supported by the Swiss NSF (Contract No. 200021-122054, 200020-140345 and MaNEP). A.D.B. received support from NSERC, FQRNT and the Canada Research Chair Foundation. Work at LANL was performed under the auspices of the US DOE, Office of Basic Energy Sciences, Division of Materials Sciences and Engineering.
Author information
Authors and Affiliations
Contributions
S.G. and M.K. conceived and led the project. S.G., M.B., J.L.G., E.R., N.E., C.N. and M.K. carried out the experiments. M.B. incorporated the piezoelectric sample rotator into the set-up. E.D.B and J.D.T. grew and characterized the CeCoIn5 single-crystal. S.G. analysed the data. S.G., J.L.G. and M.K. wrote the manuscript with input from all co-authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Information (PDF 538 kb)
Rights and permissions
About this article
Cite this article
Gerber, S., Bartkowiak, M., Gavilano, J. et al. Switching of magnetic domains reveals spatially inhomogeneous superconductivity. Nature Phys 10, 126–129 (2014). https://doi.org/10.1038/nphys2833
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys2833
This article is cited by
-
Single-domain stripe order in a high-temperature superconductor
Communications Physics (2022)
-
Nature of the spin resonance mode in CeCoIn5
Communications Physics (2020)
-
Distinct domain switching in Nd0.05Ce0.95CoIn5 at low and high fields
Scientific Reports (2018)
-
Fulde–Ferrell State in Spin–Orbit-Coupled Superconductor: Application to Dresselhaus SOC
Journal of Low Temperature Physics (2018)
-
Robust upward dispersion of the neutron spin resonance in the heavy fermion superconductor Ce1−xYbxCoIn5
Nature Communications (2016)