Abstract
It is established theoretically that an ordered state with continuous symmetry is inherently unstable to arbitrarily small amounts of disorder1,2. This principle is of central importance in a wide variety of condensed systems including superconducting vortices3,4, Ising spin models5 and their dynamics6, and liquid crystals in porous media7,8, where some degree of disorder is ubiquitous, although its experimental observation has been elusive. On the basis of these ideas, it was predicted9 that 3He in high-porosity aerogel would become a superfluid glass. We report here our nuclear magnetic resonance measurements on 3He in aerogel demonstrating destruction of long-range orientational order of the intrinsic superfluid orbital angular momentum, confirming the existence of a superfluid glass. In contrast, 3He-A generated by warming from superfluid 3He-B has perfect long-range orientational order providing a mechanism for switching offthis effect.
Similar content being viewed by others
Main
Close to the absolute zero of temperature, liquid 3He condenses into a p-wave superfluid of Cooper pairs resulting in two phases with fundamentally different symmetry: the isotropic B-phase and an anisotropic A-phase. In zero magnetic field, 3He-A appears in a small corner of the pressure versus temperature phase diagram shown in Fig. 1d. Its anisotropy, a paradigm for more recently discovered unconventional superconductors10, is characterized by the orientation of its order parameter defined by orbital angular momentum and spin induced by magnetic field,  and
and  . The spin is necessarily aligned with an applied magnetic field, H; however, the orbital angular momentum has continuous rotational symmetry. That symmetry can be broken, for example, at a wall or interface to which
. The spin is necessarily aligned with an applied magnetic field, H; however, the orbital angular momentum has continuous rotational symmetry. That symmetry can be broken, for example, at a wall or interface to which  must be perpendicular, thereby defining a preferred direction on a macroscopic scale.
must be perpendicular, thereby defining a preferred direction on a macroscopic scale.
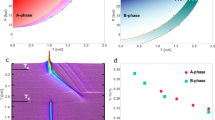
a,b, Numerical simulation of a 98% aerogel29 using a diffusion-limited cluster aggregation algorithm. Red arrows represent the orbital angular momentum distribution for a LIM state, uniform on a short length scale, ξLIM, called the LIM length, but disordered on a length scale smaller than the dipole length, ξD∼8 μm. c, Geometry of the experimental set-up. The cylinder axis of the aerogel sample and the radiofrequency field H1 are both along the y axis whereas the external magnetic field, H, is oriented along the vertical z axis. d, Pressure versus temperature phase diagram for superfluid 3He for H = 196 mT imbibed in an isotropic aerogel21, the same as for the present work. The open squares are the superfluid phase transitions and the open circles are the B- to A-phase transitions on warming. The solid red curves in the background correspond to Tc and TBA for pure 3He in zero magnetic field.
Volovik proposed9 that this long-range orientational coherence of angular momentum would be destroyed by random microscopic disorder that can be realized if the 3He is imbibed in highly porous silica aerogel as shown in our simulation Fig. 1a,b. This sensitivity to small amounts of disorder on a microscopic scale was discussed by Larkin1 and Imry and Ma2 for a broad range of physical phenomena3,4,5,6,7,8 and we refer to this as the LIM effect. If this proposal is correct then in the LIM state the order parameter structure of the superfluid will be completely hidden, a behaviour of potential significance for understanding exotic superconductors such as URu2Si2 (ref. 11).
We use nuclear magnetic resonance (NMR) to look for the LIM state of superfluid 3He-A, directly interrogating the orientation of  by measuring the Leggett shift12 of the NMR spectrum, ΔωA. In pure 3He this frequency shift is proportional to the nuclear dipole energy,
by measuring the Leggett shift12 of the NMR spectrum, ΔωA. In pure 3He this frequency shift is proportional to the nuclear dipole energy,  , where
, where  is a spin-space vector constrained to be perpendicular to
is a spin-space vector constrained to be perpendicular to  while minimizing FD. This shift is strongly temperature dependent, but for an orbital glass it should be very small, or ideally zero (Supplementary Information) as we report here.
while minimizing FD. This shift is strongly temperature dependent, but for an orbital glass it should be very small, or ideally zero (Supplementary Information) as we report here.
Leggett interpreted a shift in the NMR spectrum, centred at the frequency ωA(T), equation (1), as evidence of orientational order12,

in the absence of any external influences on  . A global minimum of dipole energy corresponds to
. A global minimum of dipole energy corresponds to  giving a maximal frequency shift at large magnetic fields (H>30 G),
giving a maximal frequency shift at large magnetic fields (H>30 G),

where ωL is the NMR frequency of the free atom. The longitudinal resonance frequency, ΩA, is proportional to the amplitude of the maximum energy gap, going to zero at the transition temperature, Tc, as is the case for all superconductors. In the presence of external fields such as aerogel-induced disorder, the dipole energy and the frequency shift in equation (2) depend on the orientations of  ,
,  and H (Supplementary Information).
and H (Supplementary Information).
Previous NMR studies of superfluid 3He in aerogel have resulted in a wide range of temperature-dependent frequency shifts accompanied by significant broadening of the NMR line suggestive of a distribution in ΔωA (refs 13, 14, 15, 16, 17, 18, 19). It is likely that macroscopic inhomogeneity and anisotropy in the aerogel influence the orientation of  (Supplementary Information). To avoid this problem, we have grown highly homogeneous isotropic aerogel with a 98.2% porosity that we have shown to be free of strain with an accuracy of 0.012% (refs 20, 21) using optical birefringence before and after the NMR experiments. The aerogel sample has a cylindrical shape as shown in Fig. 1c, with magnetic field, H, along the vertical z axis. Warming from our lowest temperatures we identified two superfluid aerogel phases21, first the B (isotropic)-phase and then the A (axial)-phase as shown in Fig. 1d, familiar from pure 3He, but with a 25% suppression of the order parameter amplitude at the pressure P = 26.1 bar. In the present work, we perform NMR measurements comparing warming and cooling following the horizontal black dashed line in Fig. 1d through all of the superfluid transitions at P = 26.3 bar.
(Supplementary Information). To avoid this problem, we have grown highly homogeneous isotropic aerogel with a 98.2% porosity that we have shown to be free of strain with an accuracy of 0.012% (refs 20, 21) using optical birefringence before and after the NMR experiments. The aerogel sample has a cylindrical shape as shown in Fig. 1c, with magnetic field, H, along the vertical z axis. Warming from our lowest temperatures we identified two superfluid aerogel phases21, first the B (isotropic)-phase and then the A (axial)-phase as shown in Fig. 1d, familiar from pure 3He, but with a 25% suppression of the order parameter amplitude at the pressure P = 26.1 bar. In the present work, we perform NMR measurements comparing warming and cooling following the horizontal black dashed line in Fig. 1d through all of the superfluid transitions at P = 26.3 bar.
The phase transitions from B to A on warming, and A to B on cooling, are identified by a discontinuity in nuclear magnetic susceptibility, χA(B), characteristic of a first order thermodynamic transition (Fig. 2a). The transitions are very sharp on both warming and cooling, with transition width ≈0.2% Tc, indicative of a highly homogeneous sample21, with typical NMR spectra shown in Fig. 2b. In Fig. 2c we provide an explicit demonstration that the A-phase obtained on warming is indeed the axial superfluid state by measuring its frequency shift as a function of the NMR tip angle, β (Methods), and comparing with theory22.
a, Liquid susceptibility relative to the normal state on warming (open red circles) and cooling (filled blue circles) versus reduced temperature in H = 196 mT. The data are spaced at ≈2 μK intervals on warming and ≈15 μK on cooling. The liquid susceptibility was obtained after subtracting the contribution from the several layers of solid 3He adsorbed to the surface of aerogel, well known to have a Curie–Weiss temperature dependence13,21,30. The jump in susceptibility on cooling or warming marks first-order transitions, TAB (TBA). The transition temperature Tc is determined as the point of onset of NMR frequency shifts. b, NMR spectra for 3He in aerogel in the normal state (red dashed curve) and the A-phase (black curve), obtained in H = 196 mT and P = 26.3 bar on warming from the B-phase at T/Tc = 0.85. c, Frequency shift versus NMR tip angle β for the A-phase nucleated from the B-phase in H = 196 mT (green circles). The dash–dot blue line is the bare Larmor frequency, ωL, and the dashed black curve is the fit to the theory22 for the dipole ordered axial state.
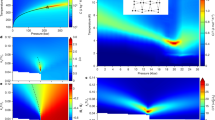
The warming transitions shown in Fig. 3 have quadratic field dependence, as expected from Ginzburg–Landau theory23,24, precisely mimicked by cooling transitions that supercool by ∼300 μK, an interval that is independent of magnetic field. Extrapolation of the warming transition, TBA(H), to zero field gives TBA(0)−Tc = 0.8±16.3 μK, indicating that for H = 0, the equilibrium state is the isotropic B-phase.
Superfluid phase diagram T(H2) for 3He at a pressure of P = 26.3 bar, for warming from the B-phase (upper panel) contrasted with cooling from the normal fluid (lower panel). The solid black line is Tc = 2.213 mK, independent of the magnetic field. The red circles are TBA corresponding to B- to A-phase transitions on warming; the blue crosses are TAB, the A- to B-phase transition after supercooling uniformly by ≈300 μK. The precise parallel behaviour of TAB(H2) and TBA(H2) indicates that the two phases, formed by warming from the B-phase and by cooling from the normal fluid, are the same state.
In Fig. 4a we show our measurements of the temperature dependence of the frequency shift of the A-phase, ΔωA (equation (2)), on cooling from the normal state (blue circles) compared with warming from the B-phase (red circles). This history dependence is unprecedented. At first glance it might seem that our observation of exactly zero shift on cooling corresponds to a strongly inhomogeneous distribution of frequency shifts that average to zero. However, the NMR line shape is identical to the normal state, evident from the linewidth in Fig. 4b, ruling out an inhomogeneous distribution of shifts. Rather, we infer that cooling from the normal state generates a disordered, but spatially homogeneous, superfluid order parameter in the predicted LIM state25. In contrast, the A-phase produced by warming from the B-phase (Fig. 2b) has a uniform frequency shift corresponding to an axial state with the minimum possible dipole energy21 shown by the black dashed curve in Fig. 4a. As in the case of pure 3He, this behaviour is a manifestation of long-range orientational order. A possible reason for maximal order in the warming experiment can be associated with the presence of a phase boundary at this first-order transition, orienting the angular momentum12,26 and breaking rotational symmetry during the formation of the A-phase, thereby inhibiting a LIM state. Another possibility is that the LIM state is disfavoured at low temperatures, an explanation that will require theoretical justification. In addition, it is worth noting that the superfluid transition from the normal state in aerogel is a second-order thermodynamic transition and has no known hysteresis on cooling compared with warming27.
Comparison of spectra for cooling and warming in H = 196 mT with small NMR tip angle β = 8° versus reduced temperature. a, Frequency shift on cooling (blue circles) from the normal state compared with warming (red circles) from the B-phase. The black dashed line is the frequency shift of the dipole-ordered axial state having an order parameter suppression of 25%. This suppression was inferred from the frequency shift measurements in the B-phase21 and the theoretically defined ratio of the shift of the isotropic state to the axial state for a dipole-ordered configuration,  , given by the Leggett relation12 and equation (2), ΩB2/ΩA2 = (5/2)(χAΔB2/χBΔA2). The red solid (green dash–dot) curve corresponds to the average frequency shift of a random 2D-disordered (3D-disordered) state. b, The additional contribution to the NMR linewidth beyond that of the normal state measured on cooling (blue circles). The linewidth data for warming are the same (Fig. 2b) but are omitted for clarity. The red solid (green dash–dot) curve is the linewidth of a simulated random 2D-disordered (3D-disordered) state.
, given by the Leggett relation12 and equation (2), ΩB2/ΩA2 = (5/2)(χAΔB2/χBΔA2). The red solid (green dash–dot) curve corresponds to the average frequency shift of a random 2D-disordered (3D-disordered) state. b, The additional contribution to the NMR linewidth beyond that of the normal state measured on cooling (blue circles). The linewidth data for warming are the same (Fig. 2b) but are omitted for clarity. The red solid (green dash–dot) curve is the linewidth of a simulated random 2D-disordered (3D-disordered) state.
The direction of  for 3He in the presence of aerogel should be locally uniform at least over a sufficiently small length scale ξLIM (Fig. 1a) that depends on the degree of disorder; Volovik estimated this to be ∼1 μm (ref. 25 and Supplementary Information). The direction of
for 3He in the presence of aerogel should be locally uniform at least over a sufficiently small length scale ξLIM (Fig. 1a) that depends on the degree of disorder; Volovik estimated this to be ∼1 μm (ref. 25 and Supplementary Information). The direction of  must be uniform over a distance ξD ∼8 μm (Fig. 1b)28, called a dipole length determined by the balance between dipole energy and gradient energy. In the limit that ξLIM<ξD,
must be uniform over a distance ξD ∼8 μm (Fig. 1b)28, called a dipole length determined by the balance between dipole energy and gradient energy. In the limit that ξLIM<ξD,  is randomly oriented with respect to
is randomly oriented with respect to  . As a result, the frequency shift collapses to zero from its equilibrium value expressed by equation (2) and the linewidth of the NMR spectrum will be identical to that of the normal state25 (Supplementary Information). In the other limit, ξLIM>ξD,
. As a result, the frequency shift collapses to zero from its equilibrium value expressed by equation (2) and the linewidth of the NMR spectrum will be identical to that of the normal state25 (Supplementary Information). In the other limit, ξLIM>ξD,  can follow the projection of
can follow the projection of  onto the plane perpendicular to H. Then the NMR spectrum will be inhomogeneously broadened and, in general, the average frequency shift will be non-zero. It has been established17 that macroscopic strain in aerogel orients
onto the plane perpendicular to H. Then the NMR spectrum will be inhomogeneously broadened and, in general, the average frequency shift will be non-zero. It has been established17 that macroscopic strain in aerogel orients  over length scales larger than ξD, so that inhomogeneity or anisotropy in partially strained samples18,19 might obscure the LIM effect.
over length scales larger than ξD, so that inhomogeneity or anisotropy in partially strained samples18,19 might obscure the LIM effect.
In the LIM state, the orbital angular momentum has no preferred direction down to and below the 10 μm scale given by the dipole length, ξD, that is, ξLIM<ξD. As such it is very different from a macroscopically inhomogeneous state induced by non-uniformity in density or anisotropy in the aerogel. To illustrate the latter, we consider two models: the 2D-disordered state where the orbital angular momentum is randomly disordered in a plane, for example, the x z or y z-plane (Fig. 1c); and the 3D-disordered state where the orbital angular momentum is random in three dimensions.
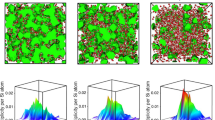
To compare our measurements with possible macroscopic distributions of angular momentum we have simulated the NMR spectra for these two models by calculating the convolution of the normal-state spectrum with spectra corresponding to the probability distribution for the orientation of the order parameter in each model. The result in Fig. 5 for the 3D-disordered state is the green dash–dot curve; the red solid curve is for 2D disorder. We obtained the frequency shift from the first moment of the simulated NMR spectrum and we calculated the linewidth from the second moment (Supplementary Information). In both cases, we compared results with our measurements in Fig. 4.
Simulated NMR spectra for 2D-disordered and 3D-disordered distributions of  compared with measured spectra in the normal state (dashed curve) and in the A-phase on cooling (blue curve) in H = 196 mT at a temperature of T/Tc = 0.85. A LIM state spectrum should have no frequency shift nor linewidth broadening compared to the normal state spectrum, as is evident in our measured spectra. However, the simulated 2D-disordered spectrum (red solid curve) and the 3D-disordered spectrum (green dash–dot curve) are significantly different, notably with an increase in linewidth in both cases and an increase in shift for 3D disorder.
compared with measured spectra in the normal state (dashed curve) and in the A-phase on cooling (blue curve) in H = 196 mT at a temperature of T/Tc = 0.85. A LIM state spectrum should have no frequency shift nor linewidth broadening compared to the normal state spectrum, as is evident in our measured spectra. However, the simulated 2D-disordered spectrum (red solid curve) and the 3D-disordered spectrum (green dash–dot curve) are significantly different, notably with an increase in linewidth in both cases and an increase in shift for 3D disorder.
The 3D-disordered state has a positive shift that deviates from the data for both warming and cooling experiments (green dash–dot curve, Fig. 4). However, the 2D-disordered state (red solid curve) has zero frequency shift, indistinguishable from our cooling measurements and that of the LIM state. On the basis of frequency shift alone it is impossible to identify a LIM superfluid glass as distinct from a 2D macroscopically disordered distribution of the angular momentum. On the other hand, the linewidths for both the 2D-disordered and the 3D-disordered states have significant increases according to our simulation as compared with a LIM state. Our observations are inconsistent with models having significant macroscopic inhomogeneity, supporting the conclusion that we have observed the 3D-LIM effect for superfluid 3He-A when it is cooled from the normal state.
In earlier NMR work on 3He in anisotropic aerogels, Elbs et al. 18 and Dmitriev et al.19 report evidence for a 2D-LIM effect. The spectra of ref. 19 for three different samples have some similarity to our model calculation for a 3D macroscopically disordered state; that is, they exhibit positive frequency shifts of various amounts for three different samples and significant linewidth broadening compared with the normal state. Nonetheless, Dmitriev et al. performed NMR tip angle and magnetic field orientation experiments and reported that these are consistent with a 2D-LIM state, indicating that there is a LIM effect present, but superposed with effects of macroscopic inhomogeneity in the aerogel.
Finally, we note that in the absence of our ability to switch off the LIM effect, we would not have been able to detect the presence of a superfluid until it appeared suddenly on cooling as a very unusual first-order transition to the B-phase. For sufficiently large magnetic fields such as to suppress the B-phase, evidence from NMR spectra for superfluid 3He would be completely hidden.
Methods
The aerogel sample is the same as we used previously21, having a cylindrical shape (Fig. 1c), 4.0 mm in diameter and 5.1 mm long, with a measured porosity of 98.2%. It was grown using the one-step sol–gel method20 and characterized thoroughly with both optical-birefringence, cross-polarization techniques and, on similarly prepared samples, small-angle X-ray scattering20,21. We found the aerogel to be uniformly isotropic with resolution better than 20 μm2. We performed pulsed NMR experiments at a pressure P = 26.3 bar in a magnetic field range from H = 49.9 to 196 mT. The H1 field that generates the radiofrequency pulse was oriented parallel to the cylindrical axis. The radiofrequency pulse tips the nuclear magnetization by an angle β away from the external field. A Fourier transform of the free induction decay signal of the magnetization in the time domain was phase corrected to obtain the absorption spectrum. The magnetic susceptibility, χ, was determined from the numerical integral of the phase-corrected absorption spectrum. Linewidths were calculated from the square-root of the relative second moment of the spectrum. The sample was cooled by adiabatic demagnetization of PrNi5 to a minimum temperature of 650 μK and NMR measurements with a constant small tip angle β were performed while the sample warmed or cooled slowly through all of the superfluid transitions, at varying rates of ∼ 3–10 μK h−1. Thermometry was based on 195Pt NMR calibrated relative to the known transition temperatures of pure 3He.
References
Larkin, A. I. Effect of inhomogeneities on the structure of the mixed state of superconductors. JETP Lett. 31, 784–786 (1970).
Imry, Y. & Ma, S. Random-field instability of the ordered state of continuous symmetry. Phys. Rev. Lett. 35, 1399–1401 (1975).
Gingras, M. J. P. & Huse, D. A. Topological defects in the random-field XY model and the pinned vortex lattice to vortex glass transition in type-II superconductors. Phys. Rev. B 53, 15193–15200 (1996).
Emig, T., Bogner, S. & Nattermann, T. Nonuniversal quasi-long-range order in the glassy phase of impure superconductors. Phys. Rev. Lett. 83, 400–403 (1999).
Simon, J. et al. Quantum simulation of antiferromagnetic spin chains in an optical lattice. Nature 472, 307–312 (2011).
Fisher, D. S., Doussal, P. L. & Monthus, P. Nonequilibrium dynamics of random field Ising spin chains: Exact results via real space renormalization group. Phys. Rev. E 64, 066107 (2001).
Radzihovsky, L. & Toner, J. Smectic liquid crystals in random environments. Phys. Rev. B 60, 206–257 (1999).
Bellini, T. et al. Nematics with quenched disorder: What is left when long range order is disrupted? Phys. Rev. Lett. 85, 1008–1011 (2000).
Volovik, G. E. Glass state of superfluid 3He-A in an aerogel. JETP Lett. 63, 301–304 (1996).
Norman, M. R. Unconventional superconductivity. http://arxiv.org/abs/1302.3176 (2013).
Mydosh, J. A. & Oppeneer, P. M. Colloquium: Hidden order, superconductivity, and magnetism: The unsolved case of URu2Si2 . Rev. Mod. Phys. 83, 1301–1322 (2011).
Leggett, A. J. A theoretical description of the new phases of liquid 3He. Rev. Mod. Phys. 47, 331–414 (1975).
Sprague, D. T. et al. Homogeneous equal-spin pairing superfluid state of 3He in aerogel. Phys. Rev. Lett. 75, 661–664 (1995).
Barker, B. I., Lee, Y., Polukhina, L. & Osheroff, D. D. Observation of a superfluid 3He A-B phase transition in silica aerogel. Phys. Rev. Lett. 85, 2148–2151 (2000).
Baumgardner, J. E. & Osheroff, D. D. Phase diagram of superfluid 3He in 99.3% porosity aerogel. Phys. Rev. Lett. 93, 155301 (2004).
Nakagawa, H. et al. Equal-spin-pairing superfluid phase of 3He in an aerogel acting as an impurity. Phys. Rev. B 76, 172504 (2007).
Kunimatsu, T. et al. Orientation effect on superfluid 3He in anisotropic aerogel. JETP Lett. 86, 216–220 (2007).
Elbs, J., Bunkov, Y. M., Collin, E. & Godfrin, H. Strong orientational effect of stretched aerogel on the 3He order parameter. Phys. Rev. Lett. 100, 215304 (2008).
Dmitriev, V. V. et al. Orbital glass and spin glass states of 3He-A in aerogel. JETP Lett. 91, 599–606 (2010).
Pollanen, J. et al. Globally anisotropic high porosity silica aerogels. J. Non-Cryst. Solids 354, 4668–4674 (2008).
Pollanen, J., Li, J. I. A., Collett, C. A., Gannon, W. J. & Halperin, W. P. Identification of superfluid phases of 3He in uniformly isotropic 98.2% aerogel. Phys. Rev. Lett. 107, 195301 (2011).
Brinkman, W. F. & Smith, H. Frequency shifts in pulsed NMR for 3He(A). Phys. Lett. 51, 449–450 (1975).
Thuneberg, E. V., Yip, S. K., Fogelström, M. & Sauls, J. A. Models for superfluid 3He in aerogel. Phys. Rev. Lett. 80, 2861–2864 (1998).
Halperin, W. P., Choi, H., Davis, J. P. & Pollanen, J. Impurity effects of aerogel in superfluid 3He. J. Phys. Soc. Jpn 77, 111002 (2008).
Volovik, G. E. On Larkin–Imry–Ma state of 3He-A in aerogel. J. Low Temp. Phys. 150, 453–463 (2008).
Bradley, D. I. et al. Relic topological defects from brane annihilation simulated in superfluid 3He. Nature Phys. 4, 46–49 (2008).
Bennett, R. G. et al. Modification of the 3He phase diagram by anisotropic disorder. Phys. Rev. Lett. 107, 235504 (2011).
Vollhardt, D. & Wölfle, P. The Superfluid Phases of Helium 3 (Taylor and Francis, 1990).
Pollanen, J. et al. New chiral phases of superfluid 3He stabilized by anisotropic silica aerogel. Nature Phys. 8, 317–320 (2012).
Bradley, D. I. et al. Magnetic phase transition in a nanonetwork of solid 3He in aerogel. Phys. Rev. Lett. 105, 125303 (2010).
Acknowledgements
We are grateful to V. V. Dmitriev, M. R. Eskildsen, M. J. P. Gingras, R. Ikeda, J. A. Sauls, J. Saunders, D. Vollhardt and G. E. Volovik for helpful comments and for support from the National Science Foundation, DMR-1103625.
Author information
Authors and Affiliations
Contributions
The experiment is designed by J.I.A.L., J.P. and W.P.H. Experimental work and analysis was principally carried out by J.I.A.L. assisted by J.P. and A.M.Z. with further support from C.A.C. and W.J.G. Advice and assistance were provided by W.P.H.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Information (PDF 622 kb)
Rights and permissions
About this article
Cite this article
Li, J., Pollanen, J., Zimmerman, A. et al. The superfluid glass phase of 3He-A. Nature Phys 9, 775–779 (2013). https://doi.org/10.1038/nphys2806
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys2806
This article is cited by
-
Orbital-flop transition of superfluid 3He in anisotropic silica aerogel
Nature Communications (2024)
-
Topological nodal line in superfluid 3He and the Anderson theorem
Nature Communications (2023)
-
Thermal transport of helium-3 in a strongly confining channel
Nature Communications (2020)
-
Pairing states of composite fermions in double-layer graphene
Nature Physics (2019)
-
Spin, Orbital, Weyl and Other Glasses in Topological Superfluids
Journal of Low Temperature Physics (2019)