Main

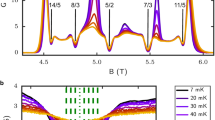
Figure 1 shows the emission spectra from a high-mobility two-dimensional electronic system (2DES) in high magnetic fields B=8–28 T, corresponding to filling factors ν<1, at a temperature T=30 mK. To better visualize the features observed, the linear magnetic field dependence has been subtracted from the photon energy. The spectra are measured on a two-dimensional electron gas (2DEG) in a modulation-doped GaAs/GaAlAs quantum well with a width of 20 nm, carrier density n=2.2×1011 cm−2, and mobility μ=3×106 cm−2 V−1 s−1. The most striking features are the oscillations in the energy of the emission line, which correlate with the fractional filling factors, and which are symmetric around filling factor ν=1/2. In particular, jumps in energy and line splittings are observed in the vicinity of filling factors and . For example, Fig. 1 shows blue-shifts of the emission energy at a magnetic field corresponding to the filling factor ν=1/3 and, symmetrically, at the filling factor ν=1. The two fillings correspond to the formation of a closed shell of composite fermions (CFs), the CF filling factor νCF=1 state.

Figure 1: Emission spectrum.
figure 1

2DEG in a modulation-doped GaAs/GaAlAs quantum well with a width of 20 nm, carrier density n=2.2×1011 cm−2, and mobility μ=3×106 cm−2 V−1 s−1 measured at T=30 mK in the range of high magnetic fields corresponding to the regime of the fractional quantum Hall effect.

Full size image

The filling-factor dependence of emission ‘anomalies’, and their behaviour with temperature is shown in Fig. 2. The colour scale reflects the emission intensity as a function of magnetic field for three different temperatures, T=30, 300 and 1,000 mK. At the lowest temperature, T=30 mK, the photoluminescence emission is shifted towards higher-energies in the vicinity of and . Emission occurs at lower energies in the intermediate regions, and in particular at filling factor ν=1/2. Strikingly, the visible sharp discontinuities in the energy of the emission line are observed at filling factors that do not correspond to those at which an incompressible liquid forms in the 2DES. This is most clearly visible in the magnetic field range 24<B<28 T, where 2/5<ν<1/3. The emission line at ν=1/3 shows internal structure, and there is a discontinuity in the magnetic field dependence of its energy. However, the jump does not occur at ν=1/3, but at a slightly higher filling factor νj (νj>1/3). The origin of these anomalies is associated with both electronic correlations and disorder. The effect of electronic correlations is clear from the temperature dependence of the emission spectrum shown in Fig. 2. The anomalies are still visible at a temperature T=300 mK, but when the sample temperature reaches 1,000 mK, the emission line is blue-shifted and shows no strong anomalies. These low temperatures, characteristic of the correlation effects associated with the fractional quantum Hall effect, are to be compared with other energy scales in the problem: the cyclotron energy ωc=R y(2/(l0/a0)2) and the exchange energy , where R y is the effective Rydberg, l0=25 nm B−1/2 is the magnetic length, and a0 is the effective Bohr radius. For B=25.5 T, the cyclotron energy is 5×105 mK and exchange energy is 3×105 mK, several orders of magnitude larger than the energy required to overcome the fractional quantum-Hall-effect gaps. The effect of disorder is harder to quantify but is clearly very important.

Figure 2: Emission spectra.
figure 2

Contour plots representing the emission spectra of a 2DEG in a regime of the fractional quantum Hall effect for different bath temperatures of T=30, 300 and 1,000 mK. The spheres represent amplitudes of different transitions extracted from gaussian fits to the emission spectra.

Full size image

To understand the combined effect of disorder and correlations on the anomalies observed, we have carried out simultaneous transport and optical experiments. In Fig. 3a we focus on the emission spectrum for 2/5<ν<1/3 without transport, and in Fig. 3b we show the simultaneously measured emission spectrum and transverse Hall resistance. The key observations in Fig. 3a are: (1) the emission line corresponding to filling factor ν=1/3 extends over a finite magnetic field range B=25.5–28 T, and (2) the emission line is broad and has an internal structure. With the present resolution, we can see two lines: a lower energy line, marked with a black arrow, and a higher energy line, marked with a red arrow. As the magnetic field increases, or when the temperature decreases (see Fig. 2), the higher-energy (red) line gains oscillator strength and becomes the dominant emission line in the ν=1/3 phase. The emission line corresponding to the ν=1/3 phase terminates at νj (<1/3) or B=25.5 T. A new line, marked with a white arrow, appears at lower energy. The discontinuity of the emission line is also clearly visible in Fig. 3b, which shows that the appearance of the new low-energy line is associated with the end of the ν=1/3 Hall plateau. The end of the Hall plateau implies that the fractionally charged quasi-particles of the ν=1/3 phase, which for ν<νj are localized by disorder, become mobile. The presence of mobile charged carriers leads to a new emission line at a lower energy than that of the quasi-exciton emission. Such a phenomenon is well-known for doped semiconductors, where the presence of mobile charged fermions leads to the formation of charged excitons21.

Figure 3: Emission spectra.
figure 3

a, Contour plot of emission spectra of a 2DEG in the vicinity of Landau level filling factor ν=1/3 measured under weak Ar+ excitation.b, Results of simultaneous photoluminescence and transport measurements. The spectra have been measured under below-barrier excitation of stronger laser power and do not reveal all details seen in a.

Full size image

The analogies between excitons and charged excitons will now be exploited in theoretical calculations of the emission spectrum of CFs. Following earlier work22,23,24,25,26,27, we model the optical emission spectrum of a 2DES by the emission spectrum of a Haldane sphere3 (HS) with a finite number of electrons N. Details of the calculations are given in the Methods section. The HS maps an infinite two-dimensional plane threaded by a magnetic field B into a sphere, at the centre of which there is a fictitious magnetic monopole, and on the surface of which electrons are placed. The filling factor on HS is determined by the ratio of the number of electrons N to the degeneracy of the shell, g=2S+1, controlled by the number of flux quanta S. In the CF picture the ν=1/3 phase corresponds to S*=3(N−1), for example, for N=5,S*=12. Figure 4a shows the calculated energy spectra of the initial |i〉 photo-excited state with N+1 electrons and one valence hole (top), and final |f〉ν=1/3 states (bottom) as a function of total angular momentum L for N=5, S*=12 and α=0.9. The final N=5 electron spectrum at ν=1/3 shows a non-degenerate ground state at L=0 and a band of low-lying excited states |m r〉, the magnetoroton band, separated by a gap Eg from the ground state3. The energy is measured from the ground-state energy in units of the gap Eg. The initial N+1X electron spectrum is also measured from its lowest energy state in units of Eg, and shifted upwards by 5Eg for visibility. The initial exciton and electron spectrum shows a ground state and a low-lying band of excited states24,25,26,27. The low-lying band involves the valence hole and fractionally charged quasi-electrons forming a quasi-exciton complex (QX). The quasi-exciton energy depends on total angular momentum L. At L=3 and energy EQX, the quasi-exciton enters a band of other excited states and ceases to be a well-defined quasi-particle. We find the binding energy EQX to be much smaller than the binding energy of a bare exciton, and smaller than the binding energy of quasi-electrons and quasi-holes Eg forming the magnetoroton. In Fig. 4a we indicate, with triangles and arrows, the optically active final and initial states, with the size of the triangles reflecting the oscillator strength. There are many possible transitions between initial and final states, which we group into two classes: the red transitions correspond to the emission from the ground state of the initial state to the ground state of the final state at L=0, whereas the black transitions correspond to the many excited initial and excited final, magnetoroton, states. These transitions can be understood as originating from the photo-excited multiplicative states22,23,24,25 P+|g〉 (red), and P+|m r〉 (black), where |g〉 is the incompressible ground state, |m r〉 are the magnetoroton excited states, and P+ creates an exciton. The emission from the quasi-exciton ground state is dominant at T=0, whereas the emission from the higher energy quasi-exciton and magnetoroton complex grows in strength as the temperature increases and these initial states become populated. An example of the calculated emission spectrum is shown in Fig. 4b for temperature T=0.2Eg. The emission spectrum shows a main transition (red), a second transition at lower energy (black), and many other weaker transitions. The oscillator strength of the black transition increases with increasing temperature. We speculate that the observed doublet in Fig. 3a corresponds to the quasi-exciton (red arrow), and to the quasi-exciton dressed by magnetorotons (black arrow). This spectrum persists as we lower the magnetic field, and at a critical value of B=B* mobile fractionally charged quasi-electrons appear. We can simulate the appearance of the quasi-electron by reducing the degeneracy of the shell by 1. In Fig. 4c, we show the spectrum of N+1X initial (top) and N electron final (bottom) states for 2S*=11. The energies are measured from the respective ground-state energies in units of the gap Eg at ν=1/3(2S*=12). The initial state spectrum has been shifted upwards by 3Eg for better visibility. The L=2.5, sixfold-degenerate ground state in the N=5 electron spectrum can be understood as a filled lowest CF Landau level and a single CF (quasi-electron) in the second CF Landau level. The CF in the second Landau level binds to the quasi-exciton and forms a fractionally charged quasi-exciton QX−. With increasing angular momentum L the QX− increases its energy, enters the continuum of states, and disassociates into a quasi-exciton and a CF in the second CF Landau level, in agreement with recent results28. The quasi-exciton is a multiplicative state. It emits a photon (red arrow), and leaves a CF in the second CF Landau level. This transition energy is the same as the transition energy in the ν=1/3 phase, but it is only possible at an elevated temperature when the charged quasi-exciton QX− is ionized. At low temperatures, only transitions with yellow and magenta arrows are possible. The magenta transition from the charged quasi-exciton QX− leaves the CF in an excited CF Landau level, whereas the yellow, impurity-allowed, transition leaves the CF in the second CF Landau level. This results in: (1) a red-shift and doublet structure in the emission line at ν=νj, where quasi-electrons become mobile and the 2DES becomes compressible (the magnitude of the shift, that is, the difference between the ‘red’ and ‘yellow’ transition, measures the charged quasi-exciton QX− binding energy) and (2) a blue-shift and vanishing of the discontinuity with increasing temperature. These theoretical findings are consistent with experimental results, and suggest that the optically observed anomalies reported here are due to composite fermions, and corresponding quasi-excitons and fractionally charged quasi-excitons.

Figure 4: Energy levels and calculated emission spectrum.
figure 4

a, Energy levels as a function of angular momentum of the initial photo-excited system (top panel) consisting of N=5 electrons at filling factor ν=1/3 (S*=12) plus 1 exciton, and energy levels of final state N=5 electrons at ν=1/3 after the recombination of exciton (bottom panel). In the final state, the ground state at L=0 is separated by a gap from excited states (the magnetorotons). The photo-excited system shows instead a band of low-energy excited states, the QX band, with a width equal to QX binding energy EQX. The arrows and triangles indicate optically active initial and final states, with the size of the triangles reflecting oscillator strength. b, Calculated emission spectrum at temperature T=0.2Eg. The two peaks labelled with red and black arrows correspond to the two types of transitions indicated in a. c, The same as in a but for S*=11, that is, one less flux quantum on HS. The lower panel shows the degenerate ground state at L=2.5, which corresponds to ν=1/3 state plus one CF. The top panel shows the formation of degenerate bound state of QX and fractionally charged CF at L=0.5 with binding energy EQX−—fractionally charged quasi-exciton (QX−). The QX− enters the continuous band of excitations, disassociates into QX and CF, and becomes optically active.

Full size image

Methods

The single particle states |m〉 (−l<m<l) on a HS are eigenstates of angular momentum lz. The lowest energy shell corresponds to l=S, where S is proportional to the number of flux quanta piercing the surface of the HS. In the lowest (degenerate) Landau level of the HS, the initial state hamiltonian of N electrons and a single valence hole is only determined by the electron–electron interaction Vee and electron–hole attraction Veh:

The operators ci+(ci), hi+(hi) create (annihilate) the electron or valence band hole in the degenerate state |i〉=|m〉. The two-body Coulomb matrix elements are 〈i j|Vee|k l〉 for electron–electron (ee), and 〈i j|Veh|k l〉 for electron–hole (eh) scattering, respectively. In our model calculation, we obtain the e–h scattering matrix elements from the e–e scattering matrix elements as 〈i,j|Veh|k,l〉=−α〈i,k|Vee|j,l〉, where α<1 measures the weakening of the e–h attraction with respect to the electron–electron repulsion in our finite width quantum well. The N-electron-one-hole states |m1,m2,m3,…,m N;m h〉=cm N+…cm3+cm2+cm1+|0〉hm h+|0〉, are used to expand the eigenstates of the system. Diagonalizing the resulting hamiltonian matrix gives the eigenstates of the initial-state hamiltonian. For N=0 these are exciton states, and for N=1 the ground state corresponds to bound charge exciton complexes27. The recombination of one of the N electrons with a valence hole creates a photon with energy E. The recombination process is described by the electron–valence-hole pair annihilation operator . The emission spectrum from states |i〉 of the initial N electron plus one exciton X (N+1 electrons plus one valence hole) system is given by Fermi’s golden rule , where Pi is the probability of the initial state to be occupied and |f〉 is the eigenstate of the final N electrons. The N electron final-states |f〉 are obtained by diagonalizing the N electron hamiltonian. Hence, the emission spectrum probes the ground and excited CF states of the final-state hamiltonian.