Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

The extreme vulnerability of interdependent spatially embedded networks

Nature Physics volume 9, pages 667–672 (2013)Cite this article

Subjects

Abstract

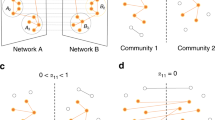
Recent studies show that in interdependent networks a very small failure in one network may lead to catastrophic consequences. Above a critical fraction of interdependent nodes, even a single node failure can invoke cascading failures that may abruptly fragment the system, whereas below this critical dependency a failure of a few nodes leads only to a small amount of damage to the system. So far, research has focused on interdependent random networks without space limitations. However, many real systems, such as power grids and the Internet, are not random but are spatially embedded. Here we analytically and numerically study the stability of interdependent spatially embedded networks modelled as lattice networks. Surprisingly, we find that in lattice systems, in contrast to non-embedded systems, there is no critical dependency and any small fraction of interdependent nodes leads to an abrupt collapse. We show that this extreme vulnerability of very weakly coupled lattices is a consequence of the critical exponent describing the percolation transition of a single lattice.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on Springer Link
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Figure 1: A system of interdependent networks is characterized by the structure (dimension) of the single networks as well as by the coupling between the networks.
Figure 2: Schematic solution of the critical point of coupled lattices and coupled RR networks.
Figure 3: Percolation transition of interdependent lattices compared with interdependent random networks.
Figure 4: The size of the abrupt collapse in coupled lattices compared with coupled random networks.
Figure 5: Mutual percolation transition in spatially embedded real-world systems.

Similar content being viewed by others

References

  1. Rosato, V. et al. Modeling interdependent infrastructures using interacting dynamical models. Int. J. Crit. Infrastruct. 4, 63–79 (2008).

    Article  Google Scholar 

  2. Peerenboom, J. P., Fischer, R. E. & Whitfield, R. in Proc. 40th Ann. Hawaii Int. Conf. Syst. Sci. 112–119 (2007); available at http://ieeexplore.ieee.org/xpl/articleDetails.jsp?arnumber=4076595.

  3. Rinaldi, S., Peerenboom, J. & Kelly, T. Identifying, understanding, and analyzing critical infrastructure interdependencies. IEEE Control. Syst. Magn. 21, 11–25 (2001).

    Article  Google Scholar 

  4. Cohen, R. & Havlin, S. Complex Networks: Structure, Robustness and Function (Cambridge Univ. Press, 2010).

    Book  Google Scholar 

  5. Buldyrev, S. V., Parshani, R., Paul, G., Stanley, H. E. & Havlin, S. Catastrophic cascade of failures in interdependent networks. Nature 464, 1025–1028 (2010).

    Article  ADS  Google Scholar 

  6. Parshani, R., Buldyrev, S. V. & Havlin, S. Interdependent networks: Reducing the coupling strength leads to a change from a first to second order percolation transition. Phys. Rev. Lett. 105, 048701 (2010).

    Article  ADS  Google Scholar 

  7. Vespignani, A. The fragility of interdependency. Nature 464, 984–985 (2010).

    Article  ADS  Google Scholar 

  8. Gao, J., Buldyrev, S. V., Havlin, S. & Stanley, H. E. Robustness of a network of networks. Phys. Rev. Lett. 107, 195701 (2011).

    Article  ADS  Google Scholar 

  9. Leicht, E. A. & D’Souza, R. M. Percolation on interacting networks. Preprint at http://arxiv.org/abs/0907.0894 (2009).

  10. Brummitt, C. D., D’Souza, R. M. & Leicht, E. A. Suppressing cascades of load in interdependent networks. Proc. Natl Acad. Sci. USA 109, 680–689 (2012).

    Article  ADS  Google Scholar 

  11. Hao, J., Cai, S., He, Q. & Liu, Z. The interaction between multiplex community networks. Chaos 21, 016104 (2011).

    Article  ADS  Google Scholar 

  12. Bashan, A., Bartsch, R. P., Kantelhardt, J. W., Havlin, S. & Ivanov, P. Ch. Network physiology reveals relations between network topology and physiological function. Nature Commun. 3, 702 (2012).

    Article  ADS  Google Scholar 

  13. Huang, X., Gao, J., Buldyrev, S. V., Havlin, S. & Stanley, H. E. Robustness of interdependent networks under targeted attack. Phys. Rev. E (R) 83, 065101 (2011).

    Article  ADS  Google Scholar 

  14. Buldyrev, S. V., Shere, N. W. & Cwilich, G. A. Interdependent networks with identical degrees of mutually dependent nodes. Phys. Rev. E 83, 016112 (2011).

    Article  ADS  MathSciNet  Google Scholar 

  15. Hu, Y., Ksherim, B., Cohen, R. & Havlin, S. Percolation in interdependent and interconnected networks: Abrupt change from second to first order transition. Phys. Rev. E 84, 066116 (2011).

    Article  ADS  Google Scholar 

  16. Parshani, R., Buldyrev, S. V. & Havlin, S. Critical effect of dependency groups on the function of networks. Proc. Natl Acad. Sci. USA 108, 1007–1010 (2011).

    Article  ADS  Google Scholar 

  17. Bashan, A., Parshani, R. & Havlin, S. Percolation in networks composed of connectivity and dependency links. Phys. Rev. E 83, 051127 (2011).

    Article  ADS  Google Scholar 

  18. Schneider, C. M., Yazdani, N., Araujo, N. A. M., Havlin, S. & Herrmann, H. J. Towards designing robust coupled networks. Sci. Rep. 3, 1969 (2013).

    Article  ADS  Google Scholar 

  19. Li, W., Bashan, A., Buldyrev, S. V., Stanley, H. E. & Havlin, S. Cascading failures in interdependent lattice networks: The critical role of the length of dependency links. Phys. Rev. Lett. 108, 228702 (2012).

    Article  ADS  Google Scholar 

  20. Gao, J., Buldyrev, S. V., Stanley, H. E. & Havlin, S. Networks formed from interdependent networks. Nature Phys. 8, 40–48 (2012).

    Article  ADS  Google Scholar 

  21. Schneider, C. M., Moreira, A. A., Andrade, J. S. Jr., Havlin, S. & Herrmann, H. J. Mitigation of malicious attacks on networks. Proc. Natl Acad. Sci. USA 108, 3838–3841 (2011).

    Article  ADS  Google Scholar 

  22. Milo, R. et al. Network motifs: Simple building blocks of complex networks. Science 298, 824–827 (2002).

    Article  ADS  Google Scholar 

  23. Alon, U. Biological networks: The tinkerer as an engineer. Science 301, 1866 (2003).

    Article  ADS  Google Scholar 

  24. Khanin, R. & Wit, E. How scale-free are biological networks. J. Comput. Biol. 13, 810–818 (2006).

    Article  MathSciNet  Google Scholar 

  25. Cohen, R., Erez, K., Ben-Avraham, D. & Havlin, S. Resilience of the internet to random breakdown. Phys. Rev. Lett. 85, 4626–4628 (2000).

    Article  ADS  Google Scholar 

  26. Dorogovtsev, S. N. & Mendes, J. F. F. Evolution of Networks: From Biological Nets to the Internet and WWW (Physics) (Oxford Univ. Press, 2003).

    Book  Google Scholar 

  27. Barthelemy, M. Spatial networks. Phys. Rep. 499, 1–101 (2011).

    Article  ADS  MathSciNet  Google Scholar 

  28. Bunde, A. & Havlin, S. Fractals and Disordered Systems (Springer, 1991).

    Book  Google Scholar 

  29. Li, D., Kosmidis, K., Bunde, A. & Havlin, S. Dimension of spatially embedded networks. Nature Phys. 7, 481–484 (2011).

    Article  ADS  Google Scholar 

  30. Stauffer, D. & Aharony, A. Introduction to Percolation Theory 2nd edn (Taylor & Francis, 2003).

    MATH  Google Scholar 

  31. Son, S., Grassberger, P. & Paczuski, M. Percolation transitions are not always sharpened by making networks interdependent. Phys. Rev. Lett. 107, 195702 (2011).

    Article  ADS  Google Scholar 

  32. Dobson, I., Carreras, B. A., Lynch, V. E. & Newman, D. E. Complex systems analysis of series of blackouts: Cascading failure, critical points, and self-organization. Chaos 17, 026103 (2007).

    Article  ADS  Google Scholar 

  33. Den Nijs, M. P. M. A relation between the temperature exponents of the eight-vertex and q-state Potts model. J. Phys. A 12, 1857–1868 (1979).

    Article  ADS  Google Scholar 

  34. Nienhuis, B. Analytical calculation of two leading exponents of the dilute Potts model. J. Phys. A 15, 199–213 (1982).

    Article  ADS  MathSciNet  Google Scholar 

Download references

Acknowledgements

We acknowledge the European EPIWORK and MULTIPLEX (EU-FET project 317532) projects, the Deutsche Forschungsgemeinschaft (DFG), the Israel Science Foundation, ONR and DTRA for financial support.

Author information

Authors and Affiliations

  1. Department of Physics, Bar Ilan University, Ramat Gan 5290002, Israel

    Amir Bashan, Yehiel Berezin & Shlomo Havlin

  2. Department of Physics, Yeshiva University, New York, New York 10033, USA

    Sergey V. Buldyrev

Authors
  1. Amir Bashan
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yehiel Berezin
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Sergey V. Buldyrev
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Shlomo Havlin
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

A.B., Y.B., S.V.B. and S.H. conceived and designed the research. Y.B. carried out the numerical simulations. A.B. developed the theory and wrote the paper with contributions from all other authors.

Corresponding author

Correspondence to Amir Bashan.

Ethics declarations

Competing interests

The authors declare no competing financial interests.

Supplementary information

Supplementary Information

Supplementary Information (PDF 276 kb)

Rights and permissions

Reprints and permissions

About this article

Cite this article

Bashan, A., Berezin, Y., Buldyrev, S. et al. The extreme vulnerability of interdependent spatially embedded networks. Nature Phys 9, 667–672 (2013). https://doi.org/10.1038/nphys2727

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/nphys2727

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing