Visualizing nodal heavy fermion superconductivity in CeCoIn₅

Abstract

Understanding the origin of superconductivity in strongly correlated electron systems continues to be at the forefront of the unsolved problems of physics¹. Among the heavy f-electron systems, CeCoIn₅ is one of the most fascinating, as it shares many of the characteristics of correlated d-electron high- T_c cuprate and pnictide superconductors^2,3,4, including competition between antiferromagnetism and superconductivity⁵. Although there has been evidence for unconventional pairing in this compound^{6,7,8,9,10,11}, high-resolution spectroscopic measurements of the superconducting state have been lacking. Previously, we have used high-resolution scanning tunnelling microscopy (STM) techniques to visualize the emergence of heavy fermion excitations in CeCoIn₅ and demonstrate the composite nature of these excitations well above T_c (ref. 12). Here we extend these techniques to much lower temperatures to investigate how superconductivity develops within a strongly correlated band of composite excitations. We find the spectrum of heavy excitations to be strongly modified just before the onset of superconductivity by a suppression of the spectral weight near the Fermi energy (E_F), reminiscent of the pseudogap state^13,14 in the cuprates. By measuring the response of superconductivity to various perturbations, through both quasiparticle interference (QPI) and local pair-breaking experiments, we demonstrate the nodal d-wave character of superconducting pairing in CeCoIn₅.

Main

CeCoIn₅ undergoes a superconducting transition at 2.3 K. Despite evidence of unconventional pairing, consensus on the mechanism of pairing and direct experimental verification of the order parameter symmetry are still lacking^6,7,8,9,11. Moreover, experiments have suggested that superconductivity in this compound emerges from a state of unconventional quasiparticle excitations with a pseudogap phase similar to that found in underdoped high- T_c cuprates^15,16,17. Previously, we demonstrated that scanning tunnelling spectroscopic techniques can be used to directly visualize the emergence of heavy fermion excitations in CeCoIn₅ and their quantum critical nature¹². Through these measurements, we also demonstrated the composite nature of heavy quasiparticles and showed their band formation as the f-electrons hybridize with the s p d-electrons starting at 70 K, well above T_c (ref. 12). This previous breakthrough, together with our recent development of high-resolution millikelvin STM, offers a unique opportunity to measure how superconductivity emerges in a heavy electron system.

Figure 1 shows STM topographs of the two commonly observed atomically ordered surfaces of CeCoIn₅ produced after the cleaving of single crystals in situ in the ultra-high vacuum environment of our millikelvin STM. We have previously shown through experiments and theoretical modelling that different surface terminations change the coupling between the tunnelling electrons and the composite heavy fermion excitations in this compound¹². Tunneling into such composite states can be influenced not only by the coupling of the tip to the spd- or f-like components of such states but also by the interference between these two tunnelling processes. On surface A, tunnelling measurements are more sensitive to the lighter component of the composite band structure and, accordingly, the spectra show evidence for a hybridization gap centred at +9 mV, as shown in Fig. 1c. At temperatures below T_c, this hybridization gap is modified by the onset of an energy gap associated with superconductivity (Fig. 1c,e), as further confirmed by its suppression with the application of a magnetic field larger than the bulk upper critical field (H_C2 = 5.0 T perpendicular to the basal plane of this tetragonal system) of CeCoIn₅ (see Supplementary Section SI).

Figure 1: Hybridization, pseudogap, and superconductivity on different surfaces of CeCoIn₅.

a,b, Topographic image with a set-point bias V = −100 mV and current I = 100 pA measured on surface A (a) and with V = −6 mV and I = 100 pA on surface B (b) of CeCoIn₅ at 245 mK. Insets in a,b zoom in on 12×12 nm² regions on their respective surfaces. The arrows in the figure indicate the in-plane crystallographic a and b directions. c,d, Corresponding conductance spectra G(V), proportional to the local electronic density of states on surface A and B carried out at temperatures above and below T_c, showing the evolution of the different energy scales (Δ_HG, hybridization gap; Δ_PG, pseudogap; Δ_SC, superconducting gap) with temperature. Spectra are offset for clarity in d. e,f, Blow up of the superconducting gap energy scale, showing the destruction of the superconducting gap in a magnetic field of H = 5.7 T>H_c2 whereas the pseudogap feature is preserved. The spectra G(V) in c,e are normalized by their corresponding junction impedances G_S.

Instead of focusing on measurements of surface A, where the tunnelling is dominated by the lighter part of the composite band, we turn to measurements of surface B. On this surface, tunnelling directly probes narrow bands of heavy excitations, which result in a peak in the density of states near E_F (Fig. 1d). Lowering the temperature from 7.2 to 5.3 K, above T_c, we find that this peak is modified by the onset of a pseudogap-like feature at a smaller energy scale. Further cooling shows the onset of a distinct superconducting gap below T_c inside the pseudogap. Measurements in a magnetic field corroborate our finding that the lowest energy scale on surface B (∼±500 μV, as shown in Fig. 1e) is indeed associated with pairing, as it disappears above H_C2, whereas the intermediate energy scale pseudogap remains present at low temperature in the absence of superconductivity at high magnetic field (Fig. 1f). This behaviour is reminiscent of the pseudogap found in underdoped cuprates, where the superconducting gap opens inside an energy scale describing strong correlations that onset above T_c. However, unlike cuprates, here we clearly distinguish between the two energy scales by performing high-resolution spectroscopy in a magnetic field large enough to fully suppress superconductivity. Detailed measurements of changes in the spectra with the magnetic field also confirm that the transition out of the superconducting state at H_C2 is first order (see Supplementary Section SI), showing that our measurements are consistent with the bulk phase diagram of CeCoIn₅.

The spectroscopic measurements suggest that electronic or magnetic correlations alter the spectrum of heavy excitations by producing a pseudogap within which pairing takes place. These measurements also show the shapes of the spectra at the lowest temperature to be most consistent with a d-wave superconducting gap, as they have a nearly linear density of states near zero energy (Fig. 1e). However, measurements on all surfaces and on several samples reveal that this d-wave gap (with a magnitude of 535±35 μV, consistent with that extracted from point contact data^18,19), is filled (40%) with low-energy excitations—a feature that cannot be explained by simple thermal broadening (determined to be 245 mK from measurements on a single-crystal Al sample, see Supplementary Section SII). The complex multiband structure of CeCoIn₅ could involve different gaps on different Fermi surface sheets, and there is the possibility that some remain ungapped even at temperatures well below T_c (ref. 20). Another contribution to the in-gap density of states could come from surface impurities, because even non-magnetic impurities perturb a nodal superconductor, as we demonstrate below. Before we address the nature of the in-gap excitations, we first demonstrate in more detail the connection between pairing and the heavy fermionic states of CeCoIn₅.

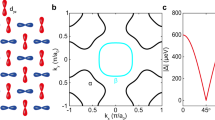
Energy-resolved spectroscopic mapping with STM can be used to measure the quasiparticle interference (QPI) to examine the heavy Fermi surface. As shown in Fig. 2a–d, features in the discrete Fourier transform (DFT) of these maps show wave vectors related to the elastic momentum transfer Q(E), connecting the initial and the final momentum states on the contours of constant energy. Previous theoretical calculations, quantum oscillation, and angle resolved photoemission spectroscopy measurements have shown CeCoIn₅ to have a complex three-dimensional (3D) band structure, with the α and β bands being the most relevant near E_F (Fig. 2e)^21,22,23. Our previous QPI measurements on surface A show features that are most consistent with 2k_F scattering originating from the α band. The QPI measurements presented here on surface B exhibit scattering wave vectors originating from a larger Fermi surface volume and are more consistent with scattering involving the β band (see Supplementary Section SIV). As QPI does not probe the Fermi surface directly, inferring a unique Fermi surface in a 3D, multi-band material without making a large number of assumptions is not possible (see Supplementary Section SV). Nevertheless, the results of QPI measurements (Fig. 2a–d), together with spectroscopic measurements (Fig. 1d), demonstrate that the superconducting instability occurs within a correlated heavy quasiparticle band of CeCoIn₅ with a large density of states at the Fermi energy.

Figure 2: Quasiparticle interference of heavy superconducting electrons.

a,b, Real space conductance map (a) and its DFT (b) at a bias of 1.5 mV measured at T = 245 mK on surface B. Colour bar in a denotes deviation from the mean. Q₁, Q₂, Q₃ correspond to the different quasiparticle scattering vectors. c, DFT at V = 3 mV (see also Supplementary Section SIII). Axes in c denote the Bragg orientation for all DFTs and for the schematic (e). d, Energy-momentum structure of Q₁, Q₂, Q₃, showing rapid dispersions reflective of mass enhancements m* = 34 m₀, 29 m₀, 23 m₀ respectively. Error bars are derived from the width of the peaks in the DFTs. e, Schematic of the band structure in the first Brillouin zone derived from refs 21, 22, 23, showing the α (magenta), β (blue) and small (orange) Fermi surfaces in the k_z = 0 (solid) and k_z = π(dashed) planes. The measured Q_1,Q₂ and Q₃ QPI scattering vectors are drawn to scale for comparison (see also Supplementary Section SIV). f–o, DFTs for selected energies in the superconducting (f–j) and normal (k–o) states. The Q-space range of the DFTs in (b,c,f–o) is ±0.5 rlu, where 1 rlu = 2π/a₀ = 2π/4.6 Å.

We focus our discussion next on the momentum structure of the superconducting gap, first by examining the conductance maps in this energy window on the same area of the sample (with the same tip) in the normal (H>H_C2) and superconducting (H = 0) states of CeCoIn₅. As the data in Fig. 2f–o demonstrate, we observe clear differences between the DFT maps in the superconducting (H = 0) and normal states (H = 5.7 T). Typically, QPI at low energies in a superconductor is associated with the scattering of Bogoliubov–de Gennes (BdG) excitations and is often analysed to obtain information about the momentum structure of the superconducting gap^24,25,26. In particular, contrasting the zero-energy DFTs in the superconducting (Fig. 2h) and normal (Fig. 2m) states, we see an enhancement of QPI at wave vector Q₃ (see also Supplementary Section SVII), suggestive of nodal BdG quasiparticles in a d-wave superconductor. However, if such features were only due to BdG-QPI, then they should exhibit a particle–hole symmetric dispersion in their energy-momentum structure away from the nodes, as seen for example in similar measurements of high- T_c cuprates²⁴. The absence of such particle–hole symmetry in our data (Fig. 2f–j), together with the large zero-bias density of states (40%, see Fig. 1e), suggests that such QPI measurements are complicated by an ungapped portion of the Fermi surface or by in-gap impurity-induced states, which are expected to have a particle–hole asymmetric structure (see measurements and discussion below). These complications, together with the complex 3D nature of the Fermi surface of this compound, make extraction of the gap function from such QPI measurements unreliable (see Supplementary Section SVI).

In contrast, using the power of STM to probe the real space structure of electronic states, it is still possible to find direct spatial signatures of the nodal character of superconductivity in CeCoIn₅ that do not require multi-parameter modelling or ad hoc assumptions to interpret. The first such signature can be found by examining the response of low-energy excitations to extended potential defects such as atomic step edges. Spectroscopic mapping with STM on approaching such steps shows direct evidence for the suppression of superconductivity in their immediate vicinity (Fig. 3a,b). This suppression is consistent with the expected response of a nodal superconductor to non-magnetic scattering (Fig. 3c), analogous to similar observations in the cuprates²⁷, and in marked contrast with our step-edge measurements of the conventional s-wave superconductor Al (see Supplementary Section SII). The data in Fig. 3d provide a direct measure of the Bardeen–Cooper–Schrieffer (BCS) coherence length²⁸ ξ_BCS = 56±10 Å, in agreement with ξ_BCS∼(ℏν_F)/(πΔ)∼60 Å using the gap observed in Fig. 1 (0.5 meV) and the Fermi velocity extracted from Fig. 2 (1.5×10⁶ cm s⁻¹).

Figure 3: Evolution of in-gap quasiparticle states approaching a step edge.

a, Topographic image (V = −100 mV, I = 100 pA) of surface A, showing a single unit-cell step edge oriented at 45° to the atomic lattice. The arrows in the figure indicate the in-plane crystallographic a and b directions. Coloured dots indicate the locations of the spectra in b. b, Evolution of the spectra near the step edge: G(V) subtracted by the spectrum far away from the step edge G(V,r = 153 Å). c, Schematic representation of nodal superconducting quasiparticles scattering off a step edge. d, Zero-bias conductance G₀(r)subtracted by the extrapolated as a function of distance from the step edge. Line represents an exponential fit to the data, where error bars denote the standard deviation on the averaged spectra. ξ_BCS denotes the characteristic decay length obtained from the fit (with a prefactor a*) in d, which is a measure of the BCS coherence length.

Application of a magnetic field can also be used to probe the local suppression of heavy fermion superconductivity in CeCoIn₅ due to the presence of vortices and the Abrikosov lattice. As shown in Fig. 4a,b, STM conductance maps can be used to directly visualize the vortex lattice in this compound, which can have different structures depending on the magnetic field. Such structural changes of the vortex lattice (transition between rhombic and square lattices) have been previously studied in neutron scattering experiments²⁹ and various theoretical models³⁰. Complementing these efforts, STM can be used to probe the electronic states within the vortex core directly, as shown in Fig. 4d, to demonstrate the presence of a zero-energy vortex bound state. Analysis of this core state demonstrates the anisotropic decay of the vortex bound state (Fig. 4c,e and see Supplementary Section SVIII), the angular average (Fig. 4e) of which determines the Ginzburg–Landau coherence length scale (ξ_GL = 48±4 Å), consistent with an independent estimate from dH_c2/$\text{d}T{|}_{T=T_{\text{C}}}$ (ref. 31). Although observation of such anisotropy is consistent with the nodal character of pairing, an understanding of the role of the underlying Fermi surface symmetry and vortex–vortex interactions is required to model the STM data in more detail.

Figure 4: Visualizing the vortex lattice and vortex-bound quasiparticle states.

a,b, Zero-bias conductance maps both taken at H = 1 T(separate field dials) and at T = 245 mK show the vortex lattice structure expected below (a) and above (b) the transition seen at this field by neutron scattering in ref. 29. The arrows in the figure indicate the in-plane crystallographic a and b directions. c, Close-up zero-bias map of the vortex lattice on surface B, showing an anisotropic square vortex core (H = 1.5 T). d, Line-cut of spectra starting from the centre of a vortex and moving radially outward at 45° to the b-axis, showing the evolution of the bound state inside the superconducting gap (H = 0.5 T). e, Radial dependence of the angularly averaged zero-bias conductance G₀ for a single vortex core at H = 1 T. Error bars (estimated from the standard deviation in the analysed map) are smaller than the marker size in e. Inset shows the angular dependence of the radially averaged zero-bias conductance, showing the four-fold anisotropy of a single vortex with higher conductance extending along the a- and b-directions (see Supplementary Section SVIII). (ξ)_GL denotes the characteristic decay length obtained from the fit (with a prefactor a*) in e, which is a measure of the angularly averaged Ginzburg–Landau coherence length.

A more spectacular demonstration of the nodal pairing character in CeCoIn₅ can be obtained from examining the spatial structure of in-gap states associated with defects on the surface of cleaved samples. The spatial structure of impurity quasi-bound states, which are mixtures of electron-like and hole-like states, can be a direct probe of the order parameter symmetry^28,32. Figure 5 shows an extended defect with a four-fold symmetric structure, which perturbs the low-energy excitations of CeCoIn₅ by inducing an in-gap state. Probing the spatial structure of these impurity states, we not only find their expected electron–hole asymmetry, but also find that their orientation is consistent with that predicted for a $d_{x^2-y^2}$ superconductor (Fig. 5b–e and Supplementary Section SIX)³². The minima (maxima) in the oscillations for hole-like (electron-like) states identify the nodes of the d-wave order as occurring at 45° to the atomic axes (Fig. 5h). In fact, these features in STM conductance maps are identical to those associated with Ni impurities in high- T_c cuprates^28,33. However, in contrast to measurements in the cuprates, we are able to determine the spatial structure that such impurities induce on the normal state by suppressing pairing at high magnetic fields. Such measurements allow us to exclude the influences of the normal state band structure, of the impurity shape, or of the tunnelling matrix element²⁸ on the spatial symmetries of the impurity bound state in the superconducting state. Contrasting such measurements for H>H_C2 (in Fig. 5f,g) with measurements on the same impurity for H = 0 (Fig. 5d,e) we directly visualize how nodal superconductivity in CeCoIn₅ breaks the symmetry of the normal electronic states in the vicinity of a single atomic defect.

Figure 5: Visualizing impurity-bound quasiparticle excitations.

a, Topographic image of an impurity on surface B (V = −6 mV, I = 100 pA). b, Model calculation for the real space structure (roughly 10 Fermi wavelengths across) of the hole-like part of the impurity bound state in a $d_{x^2-y^2}$ superconductor, reproduced from ref. 32 (Copyright (2000) by the American Physical Society). c, Electron-like state for the same impurity as in b. d–g, Local density of states obtained on the same field-of-view as a at ±195 μV in the normal (H>H_c2) and superconducting (H = 0) states, as indicated on the figure. Colour bar in d–g denotes deviation from the mean. h, Radial average of the density of states across the lobes measured in d,e, normalized to their sum, as a function of angle from the a-axis. Data at negative (positive) energy is shown in blue (red) symbols; the lines are guides to the eye. A $d_{x^2-y^2}$ gap is shown in yellow.

The appearance of a pseudogap and the direct evidence for $d_{x^2-y^2}$ superconductivity reported here, together with previous observations of the competition between antiferromagnetism and superconductivity, closely ties the phenomenology of the Ce-115 system to that of the high-temperature cuprate superconductors. An important next step in extending this phenomenology would be to explore how the competition between antiferromagnetism and superconductivity manifests itself on the atomic scale in STM measurements. Similarly, extending our studies of the electronic structure in magnetic vortices could be used to examine the competition between different types of ordering in the mixed state, and the possible development of the Fulde–Ferrell–Larkin–Ovchinnikov state in this Pauli-limited superconductor^29,34,35.

Methods

The single-crystal samples (1.5 mm×1.0 mm×0.2 mm) used for this study were grown from excess indium at Los Alamos National Laboratory, and were then cleaved along the c-axis in ultra-high vacuum at room temperature before performing STM measurements. All data shown from surface B were taken on an undoped sample of CeCoIn₅; all surface A measurements were performed on a sample with an effective doping of 0.15% Hg. Bulk transport properties of both samples are indistinguishable. Conductance measurements were made using standard a.c. lock-in techniques, with a bias applied to the sample, and were reproduced on different large, atomically flat areas of the sample, having different defect concentrations, and under multiple tunnelling conditions ranging up to two orders of magnitude in set-point current.