Imaging Cooper pairing of heavy fermions in CeCoIn₅

Abstract

The Cooper pairing mechanism of heavy fermionsuperconductors^1,2,3,4, long thought to be due to spin fluctuations^5,6,7, has not yet been determined. It is the momentum space (k-space) structure of the superconducting energy gap Δ(k) that encodes specifics of this pairing mechanism. However, because the energy scales are so low, it has not been possible to directly measure Δ(k) for any heavy fermion superconductor. Bogoliubov quasiparticle interference imaging⁸, a proven technique for measuring the energy gaps of superconductors with high critical temperatures^9,10,11, has recently been proposed¹² as a new method to measure Δ(k) in heavy fermion superconductors, specifically CeCoIn₅ (ref. 13). By implementing this method, we detect a superconducting energy gap whose nodes are oriented along k∥(±1,±1)π/a₀ directions^14,15,16,17. Moreover, for the first time in any heavy fermion superconductor, we determine the detailed structure of its multiband energy gaps Δ_i(k). For CeCoIn₅, this information includes: the complex band structure and Fermi surface of the hybridized heavy bands, the fact that largest magnitude Δ(k) opens on a high- k band so that the primary gap nodes occur at unforeseen k-space locations, and that the Bogoliubov quasiparticle interference patterns are most consistent with $d_{x^2-y^2}$ gap symmetry. Such quantitative knowledge of both the heavy band-structure and superconducting gap-structure will be critical in identifying the microscopic pairing mechanism of heavy fermion superconductivity.

Main

The heavy fermion superconductor CeCoIn₅ (ref. 13) has a crystal unit cell with a = b = 4.6 Å, c = 7.51 Å, as shown schematically in Fig. 1a, and a superconducting critical temperature T_c = 2.3 K. If antiferromagnetically ordered, the Ce³⁺ atoms would exhibit local magnetic moments μ = 0.15 μ_B (ref. 18). Although that state does not exist in the pure compound studied here, antiferromagnetic spin fluctuations do persist¹⁹. Pioneering research on CeCoIn₅, using the recently introduced heavy fermion interference imaging technique^20,21, reveals a heavy band²² at T≈20 K, in qualitative agreement with angle resolved photoemission measurements at similar temperatures^23,24. However, no detailed and quantitative determinations of the heavy fermion band structures or Fermi surfaces have been reported for this compound. In its superconducting phase, the Cooper pairs are spin singlets^25,26, so that an even parity Δ(k) is required. The magnetic field-angle dependence of thermal conductivity¹⁵ and specific heat¹⁷ are interpreted as evidence of energy-gap nodes |Δ(k)| = 0for momentum space directions k∥(±1,±1)π/a₀. A fully detailed knowledge of the k-space structure of Δ(k) is required to understand the microscopic Cooper pairing mechanism of heavy fermions. This cannot be achieved using such indirect methods, or by using photoemission because the energy resolution required is δ E<100 μeV. Motivated thus, high-resolution Bogoliubov quasiparticle scattering interference imaging has recently been mooted¹² as a promising approach for determining Δ(k) of heavy fermion superconductors, specifically for CeCoIn₅.

Figure 1: Anticipated electronic structure of a heavy fermion superconductor.

a, Schematic representation of the crystal unit cell of CeCoIn₅. b, Schematic of the typical evolution of the k-space electronic structure observed²¹ as hybridization splits the light band into two heavy bands, and the consequential effects on the density of states N(E). c, Schematic of expected evolution of the k-space electronic structure as the superconducting energy gap appears (presumably) on one of the new heavy bands. The right-hand panel shows expected changes in the N(E) due to heavy fermion Cooper pairing, here simulated for a d-wave symmetry energy gap. d, Topographic image of the termination surface of cryo-cleaved CeCoIn₅ used in this study. e, Average differential conductance spectra g(E) in the energy range of light band(s) |E|≤200 meV, measured using the lock-in technique with a bias modulation of 5 meV so that any finer energetic features are unresolvable. Data in f,g below are acquired with decreasing bias modulation compared to that in e. f, Measured average differential conductance spectra in the energy range spanning the hybridization gap ∼−4 meV<E<12 meV. The hybridization gap E_h between vertical arrows is determined directly from heavy quasiparticle scattering interference (Fig. 3), measured with bias modulation of 1.5 meV so that any finer energetic features, for example the superconducting energy gap, are unresolvable. g, Measured differential conductance spectra in the energy range spanning the superconducting gap |E|≤600 μeV, measured with a bias modulation of 70 μeV and a thermal energy resolution of 75 μeV. The colours associated with the three different energy scales in e–g are used throughout the paper to indicate the equivalent energy scales.

There are three elements of k-space electronic structure expected in a generic heavy fermion superconductor⁴. First, the high-temperature state consists of a conventional (light) electronic band, indicated schematically by the dashed curve in Fig. 1b, that coexists with localized f-electron states on each magnetic atom. At lower temperatures, hybridization between this light band and the f-electron states results in its splitting into two new heavy bands, as shown schematically by the solid blue lines in Fig. 1b. The right panel shows how the resulting very flat bands generate a greatly enhanced density-of-electronic-states N(E) within a few meV of E_F—hence the ‘heavy’ effects seen in thermodynamic studies. At least one of these heavy bands crosses E_F at the new Fermi wave vector k_F^H, as shown within the green box in Fig. 1b. It is in this region of k-space that, at even lower temperatures, the heavy quasiparticles are hypothesized to bind into heavy Cooper pairs. An energetically particle–hole symmetric superconducting energy gap Δ(k), probably of an unconventional nature^{1,2,3,4,5,6,7}, is then expected to open in the heavy quasiparticle spectrum at the Fermi surface, as shown schematically in Fig. 1c. The right panel shows the further expected changes in N(E) for a nodal Δ(k).

To search for this sequence of phenomena, we use pure CeCoIn₅ samples inserted into the cryogenic ultrahigh vacuum of a ³He-refrigerator-based spectroscopic imaging scanning tunnelling microscope²⁷ (SI-STM), and mechanically cleaved therein. Atomically flat a–b surfaces are achieved; a typical resulting topograph with visible atomic lattice a₀ = 4.6 Å (that was previously assigned to be the Ce lattice²²) is shown in Fig. 1d. On all such surfaces, the density-of-states is determined from the spatially averaged differential tunnelling conductance measured far from impurity atoms. Whereas the basic of the unhybridized ‘light’ bands is measured over the range |E|≤200 meV (Fig. 1e), the complex scattering interference features associated with the heavy band structure are only visible within the range ∼−4 meV<E<12 meV. Vertical arrows in Fig. 1f then indicate the limits of the hybridization gap E_h for CeCoIn₅, as determined directly from the heavy band scattering interference analysis in Fig. 3.

On entering the superconducting phase, develops an energy gap with a maximum value |Δ_max| = 600±50 μeV, a V-shaped that is the signature of a nodal^28,29 Δ(k), and a finite^28,29,30 N(E = 0), all as shown in Fig. 1g. Figure 2a shows a typical example of atomically resolved images g(r,E)≡dI/dV (r,E = eV) measured within the superconducting gap at E = 250 μeV, and acquired in a 32 nm×32 nm field of view (FOV). The superconducting peak-to-peak gap map Δ_pp(r) in the same FOV (Fig. 2b) reveals the electronic homogeneity of this material. In Fig. 2c we show an image of the CeCoIn₅ Abrikosov vortex array acquired at T = 250 mK, B = 3 T in a larger FOV; its shape and orientation are in excellent agreement with small-angle neutron scattering studies³¹. As all these phenomena disappear at the superconducting T_c observed in bulk measurements, the |Δ_pp| = 550±50 μeV energy gap with V-shaped N(E) is definitely that of the superconductor. Determination of the k-space structure of Δ(k) for CeCoIn₅ is then the main focus of this paper.

Figure 2: Imaging superconducting gap map and vortex lattice of CeCoIn₅.

a Typical example of g(r,E) measured below the superconducting gap edge |Δ_pp| = 550 μeV and acquired in a 32nm×32 nm FOV. b, Superconducting peak-to-peak gap map Δ_pp(r) measured between the particle–hole symmetric peaks in g(r,E) taken in same FOV as a. The homogeneity of the gap structure away from impurities is as expected in these pure materials. The inset shows a typical spectrum with arrows denoting the maximal gap, Δ_pp. c, Image of CeCoIn₅ Φ = h/2e Abrikosov vortex array at B = 3 T by measuring g(r,E = 0,3 T)−g(r,E = Δ_pp,3 T). The lattice is consistent with the square lattice reported by neutron scattering experiments³¹, taking into account the small field drift.

To proceed, we image the differential conductance g(r,E) with atomic resolution and register, and then determine g(q,E), the square root of the power spectral density Fourier transform of each image. The measurements are all carried out at 250 mK—thereby achieving an energy resolution δ E∼3.5 k_BT∼75 μeV. By using a >30 nm-square FOV we simultaneously achieve q-space resolution |δ q|<2% of the reciprocal unit cell, and a concomitant k-space resolution |δ k|<2% of the Brillouin zone. To investigate both how the light bands transform to hybridized heavy fermion states, and how superconductivity then emerges, we measure these datasets on three distinct energy scales, each of about an order of magnitude smaller energy range than the previous one, as described in the Supplementary Information. These data are used to evaluate elements of k-space electronic structure, based on the fact that elastic scattering of electrons with momentum −k(E) to +k(E) generates interference patterns occurring as maxima at q(E) = 2k(E) in g(q,E), an effect recently revealed to exist even when hybridization generates heavy fermion bands^20,21,22. In Supplementary Section SI and Fig. S1 we show the measured g(q,E) at T = 1.2 K, for −100 meV<E<30 meV, focusing on the light unhybridized electronic structure. Here the maximum intensity features move slowly and smoothly to smaller |q|-radii with increasing E, thereby revealing a light and simple tetragonal band (Supplementary Section SI and Movie S1).

Significant departures from this simple phenomenology are found to occur only within the energy range ∼−4 meV<E<12 meV. In Fig. 3a–e we next show the measured g(q,E) at T = 250 mK within this range (Supplementary Section SI). The onset of hybridization is detected as a sudden transformation of the previously unchanging structure of g(q,E) occurring at E≈−4 meV (Fig. 3b), followed by a rapid evolution of the maximum intensity features (indicated by circles and arrows Fig. 3c) towards smaller |q|-radius interference patterns. Then, in Fig. 3c we see that an abrupt jump to a larger |q|-radius occurs, followed by a second rapid diminution of interference pattern |q|-radii in Fig. 3c–e (complete phenomena shown in Supplementary Section S1 and Movie S1). These are all the expected quasiparticle interference (QPI) signatures of the appearance of hybridized heavy fermion bands. Thus, for CeCoIn₅ this approach reveals how the light conduction band is split into two heavy bands within the hybridization gap −4 meV<E_h<12 meV. To see this directly, we show in Fig. 3f,g the measured evolution of the maxima in g(q,E) for two directions in q-space. The light band (grey dots) begins to deviate near −4 meV towards the lower heavy band which crosses E_F at smaller |q| = 2|k_F^H|, and evolves quickly to even smaller |q|(blue dots). Within a few meV above E_F, the interference patterns jump to a much larger |q| and then evolve (blue dots) back towards the light band (grey dots), which they rejoin near +12 meV. This heavy band actually crosses below E = 0 at high k, producing an electron-like Fermi surface whose intra-band scattering interference generates interference patterns at low q (blue dots E<0 as |q|→0). These data (Fig. 3a–e, Supplementary Section SI), and the extracted dispersions (Fig. 3f,g) are next used to determine details of the heavy fermion band structure.

Figure 3: Determination of heavy fermion bands and Fermi surfaces at B = 0 in CeCoIn₅.

a–e, Measured g(q,E) at T = 250 mK and δ E∼75 μeV, concentrating on the heavy-fermion-forming hybridization window −4 meV<E_h<12 meV. The numbered arrows indicate locations of maxima in g(q,E) whose dispersion is identified using similarly numbered arrows in f,g and grey crosses mark the Bragg peak locations. All g(q,E) data, except those measured within the superconducting gap, are treated as described in Supplementary Section SV. f,g, Measured evolution of the light band scattering interference dispersion |q(E)| (grey circles) and its transition to two heavy bands (blue circles) each with a distinct |q(E)|. Some points are fitted on g(q,E = const) layers, whereas others are fitted from g(|q|,E) cuts (Supplementary Section SIV). The error bars are estimates based on the peak widths and the confidence intervals from the peak fits. h, Momentum-space model for the hybridization-induced heavy bands and Fermi surfaces of CeCoIn₅. Detailed parameterization is given in Supplementary Section SII. At the centre of the upper half of this panel we see the light band (grey) closing at the centre. As E = 0 is approached from above, the upper heavy band (blue) diverges from the light band and begins to disperse very rapidly outwards, crossing E = 0 at high k. The lower half of this panel shows the light band (grey) approach E = 0 from below, beginning to diverge rapidly towards low k as it crosses E = 0(blue), and then closing just above E = 0. The characteristic Fermi surface areas deduced from the data/model for the heavy bands shown in Fig. 3 are somewhat comparable to those found in quantum oscillation studies in CeCoIn₅ (refs 32, 33). However, quantitative comparison of these to the FS areas determined by quantum oscillations at high field seems, in principle, to be quite challenging, because a rapid field-induced reorganization of the band-structure occurs above B = 4.5 T. Furthermore, data on the CeCoIn₅ k-space structure measured using both SI-STM (ref. 22) and ARPES (refs 23, 24) at T∼20 K (energy resolution δ E≈3.5k_BT≈5 meV) are not inconsistent with the higher precision heavy-band determinations herein; comparison with the quantum oscillations is discussed in Supplementary Section SVI.

In general for a complex and multi-band k-space structure, achieving a deterministic inversion procedure from g(q,E) data to the complete band structure can be challenging¹¹. Here, comparison of the predicted scattering interference dispersions |q(E)| from a specific model of the heavy bands described in Supplementary Section SII and Fig. 3h, with the experimental |q(E)| data within the hybridization range E_h, reveals good agreement (Supplementary Figs S2 and S3). The critical elements in our model that lead to this agreement are the nearly parallel sections of the light band contours-of-constant-energy and the hybridization with a specifically shaped f-band. Some of these same elements of k-space structure can equally be found in ref. 12. Our model concentrates on best emulation of the key empirical phenomena of the heavy QPI data. On this basis, the g(q,E) in Fig. 3a–g are used to motivate the detailed k-space model for the heavy bands of CeCoIn₅, as shown in Fig. 3h (Supplementary Section SII). Here, within the rangeE_h, a light-hole-like band centred around Γ (or equivalently M) hybridizes with a localized f-electron band (Supplementary Section SII). The resulting lower heavy band β has a simple Fermi surface and closes quickly above E_F, whereas the upper heavy band α is highly anisotropic with a complex Fermi surface as it crosses below E_F, making it effectively electron like. Our model indicates the possibility of a small dimple that crosses back above E_F, but this is in no way critical to the subsequent analysis.The Fermi surfaces are shown as solid lines on the E = 0 planes of Fig. 3h. Their relationship with the FS areas deduced from quantum oscillations (QO) at high fields^32,33 is discussed in Supplementary Section VI.

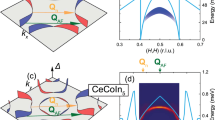
To investigate the superconductivity on the heavy bands in Fig. 3h, Fig. 4a–e shows the measured g(q,E) at T = 250 mK and |E|<300 μeV, within the superconducting energy gap. Here we see extremely rapid evolution in g(q,E) over energies of a few 100 μeV, and the appearance of a four-fold symmetric ‘nodal’ g(q,E) structure as E→0. Clearly, this g(q,E = 0) exhibits far more complexity than expected for a single-band nodal superconducting energy gap. To explore these phenomena we carry out Bogoliubov QPI simulations based on the two heavy bands, α and β (Figs 3h,4k), but now specifying their superconducting energy gaps Δ_α(k) and Δ_β(k), whose derivation is discussed below. Here the inter-nodal scattering wave vectors for the α band (coloured arrows Fig. 4k) are demonstrably consistent with the measured inter-nodal scattering vectors in g(q,E = 0) data, whereas the equivalent internodal signatures are undetected for the β band. As specific heat data show that all the main bands in CeCoIn₅ are gapped at lowest temperatures¹³, this suggests that the gap on the β band, although extant, is too small to be detected at T∼250 mK (ref. 34) because the energy uncertainty of tunnelling electrons δ E∼75 μeV probably exceeds the gap maximum. This situation also provides a simple and plausible explanation for the non-zero tunnelling conductance at E = 0. What our data do indicate is that the primary gap of CeCoIn₅ actually occurs on the high- k α-band with lines of gap-nodes along the k = (0,0)→(±π,±π)/a₀ directions, so that the dominant gap nodes in CeCoIn₅ occur at unforeseen k-space locations (Fig. 4k).

Figure 4: Momentum-space superconducting energy gap Δ(k) of CeCoIn₅.

a–e, Measured g(q,E) at T = 250 mK and δ E∼75 μeV, within the heavy fermion superconductivity energy window −600 μeV<E<600 μeV. The raw data were symmetrized to increase the signal-to-noise ratio. The Bragg peak location (2π,0) is indicated in a, and crosses mark the Bragg peak locations in f–j. f–j, Corresponding Bogoliubov QPI simulations of g(q,E) at the same energies as in a–e (Supplementary Section SII) on the two bands as shown in Figs 3h, 4k, and for superconducting gaps given approximately by Δ_β(θ_k) = 0 and a $d_{x^2-y^2}$ symmetry gap having Δ_α(θ_k) = Acos(2θ_k) with A = 600 μeV. k, Fermi surfaces and energy gaps of CeCoIn₅ modelled using heavy QPI in Fig. 3 (Supplementary Section SII). The superconducting energy gaps Δ_i(k) used to achieve the most successful Bogoliubov QPI simulations are shown in red. Although a zero gap is shown on the β sheet, our data only constrain Δ_β to be less than our energy resolution of 75 μeV; previous thermodynamic studies¹³ show that both α and β bands are gapped at the lowest temperatures. As in c, the internodal scattering vectors consistent with the data are show as solid blue arrows while the Friedel oscillation wave vectors of the ungapped (at 250 mK) Fermi surface regions are shown as dashed blue lines (details in Supplementary Section SII). l, Measured |Δ(θ_q)| using techniques as described in text (Supplementary Section SIII) and its comparison with the simplest multi-band gap structure Δ_β(θ_k)≈0 and Δ_α(θ_k) = Acos(2θ_k) with A = 600 μeV that we find to be consistent with all the Bogoliubov g(q,E) data herein. The arrow identifies the strong departures from this simple gap function. Error bars are estimates based on the peak widths and the confidence intervals from the peak fits, as described in Supplementary Section SV.

Next we consider a detailed comparison of the measured g(q,E) data for |E|≤600 μeV at T∼250 mK with theoretical simulations of Bogoliubov QPI in g(q,E) using the α,β Fermi surfaces described in Figs 3h,4k. The simulations have been carried out using various symmetries for the superconducting energy gaps and are described in full detail in Supplementary Section SII. Our model with superconducting gaps of $d_{x^2-y^2}$ symmetry given approximately by |Δ_β(θ_k)|<50 μeV and Δ_α(θ_k) = Acos(2θ_k), with A = 600±50 μeV, yields a set of simulated g(q,E) that are far more consistent with the experimental data than any of the other models we have considered (Supplementary Fig. S5, Supplementary Section SII). For comparison, a direct experimental estimation of |Δ(θ_k)| can be achieved by using g(q,E) data in a procedure largely independent of the Fermi surface details. To obtain the angle θ_q dependence of the energy gap that opens at T_c, we integrate the total spectral weight g(q,E) within a given |δ q| range containing the Fermi surface, with the lowest |q| large enough to exclude effects of heterogeneity and the largest |q| small enough to exclude the Bragg peaks. A clear gap Δ(θ_q) is observed to open in this integral of g(q,E) on passing below T_c, as demonstrated in Supplementary Section SIII. In Fig. 4l we plot the measured energy gap |Δ(θ_q)| from this technique (red dots) along with Δ_α(θ_k) = |Acos(2θ_k)| with A = 600 μeV (solid line). Their agreement provides strong independent motivation for our gap structure model (Fig. 4k and Supplementary Section SII). A final stimulating observation is that the departures in the Δ(θ_q) at a higher energy from the simple Δ_α(θ_k) = Acos(2θ_k) might be expected if high q scattering between these locations on the α band is involved in the Cooper pairing mechanism.

Overall, these data represent the first measurements of the k-space structure of the superconducting energy gaps Δ_i(k) for any heavy fermion superconductor. They reveal a wealth of previously unknown information on the Δ_i(k) of CeCoIn₅, including: the complex Fermi surface of the hybridized heavy bands (Figs 3h,4k); the spectroscopic signature of four nodal lines in |Δ(k)| oriented along k = (±1,±1)π/a₀ or Ce–Ce directions^14,15,16,17; that the dominant Δ(k) opens on the α heavy band at high k (Fig. 4k); the unforeseen k-space locations of the dominant gap nodes that ensues (Fig. 4k); that the Bogoliubov QPI patterns are most consistent with $d_{x^2-y^2}$ gap symmetry; and evidence for a departure in Δ(k) from a simple cos(2θ_k) dependence at regions of the α band connected by q≈(±1,±1)π/a₀ (Fig. 4k,l). These detailed multi-band Δ_i(k) data provide information critical for determining the microscopic mechanism of unconventional superconductivity in CeCoIn₅. Moreover, the novel approach proposed in ref. 12, and established here, reveals an exciting new opportunity to achieve a quantitative understanding of the microscopic physics of heavy fermion superconductivity in general.

Methods

High-quality CeCoIn₅ single crystals were grown at BNL (details in ref. 13). Magnetization measurements before sample insertion into the STM show a sharp transition with T_c = 2.1 K. The samples were mechanically cleaved in cryogenic ultrahigh vacuum at T∼10 K and directly inserted into the STM head at 4.2 K. Etched atomically sharp and stable tungsten tips with an energy-independent density of states are used. Differential conductance measurements throughout used a standard lock-in amplifier. See Supplementary Information for additional details on data treatment and extraction.