Main

Whereas the dynamics of semiclassical two-level systems under the influence of a pulsed external electromagnetic field was observed decades ago in many-spin NMR experiments, a completely classical analogue remained elusive for a long time. Such a classical two-mode system can for example be created using two optical cavity modes14 or mechanical resonators. Only recently, several approaches were employed to achieve purely mechanical resonant coupling either between separate resonators15,16,17 or different modes of the same resonator10,18 in the classical regime. So far, the pulsed coherent control of the system was prevented by weak coupling, low quality factors or the lack of a sufficiently strong and fast tuning mechanism.

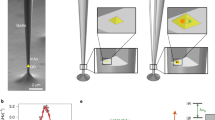
We present the successful implementation of a purely mechanical, classical two-level system, consisting of the two coupled fundamental flexural modes of a nanomechanical resonator with coherent time-domain control (see also the experiments independently performed using parametric coupling19 instead of the linear coupling employed here). To this end, we use a 250 nm wide and 100 nm thick, strongly stressed20 silicon nitride string resonator with a length of 50 μm dielectrically coupled to a pair of electrodes used for detection21 as well as actuation and tuning22. The two fundamental flexural modes of the mechanical resonator oscillating in the out-of-plane and in-plane direction (Fig. 1a) are linearly coupled by cross-derivatives of the strong inhomogeneous electric field generated between the electrodes (see the Supplementary Information of ref. 10 for a theoretical analysis). A constant d.c. voltage of −15 V is employed to dielectrically tune the system close to the resulting avoided crossing, while the signals generated by an arbitrary waveform generator (AWG) enable time-resolved control in the vicinity of the avoided crossing (Fig. 1b,c). Both voltages are added, combined with the radiofrequency actuation at a bias-tee, and applied to one electrode. The other electrode is connected to a 3.6 GHz microstrip cavity, enabling heterodyne detection of the string deflection21 after addition of a microwave bypass capacitor at the first electrode22. These components, as well as the mechanical resonator, are placed in a vacuum of ≤10−4 mbar and the system is cooled to 10.00±0.02 K to improve the temperature stability as well as the cavity quality factor. The microwave cavity is interfaced to the readout with a single coaxial cable and a circulator.

Figure 1: Nanoelectromechanical system.
figure 1

a, Scanning electron micrograph showing oblique view of the 50 μm long silicon nitride string (green) and the adjacent, 1 μm wide gold electrodes (yellow), processed on top of the SiN. b, Electrical set-up. The output of the AWG and a d.c. tuning voltage are added and combined with the radiofrequency drive at a bias-tee. The second capacitor acts as a bypass providing a microwave (μw) ground path for the microwave detection21. c, Resonance frequencies of the out-of-plane (Out) and in-plane (In) mode of the resonator are controlled by the AWG voltage at a constant d.c. tuning voltage of −15 V. The black circle marks the initialization state at 0 V and the frequency of the radiofrequency drive, and the green and blue circles correspond to the lower and upper state of the classical two-level system, respectively, separated by Ω.

Full size image

When the system is driven by an external white-noise source and the AWG output voltage is swept, the avoided crossing of the two modes shown in Fig. 1c can be mapped out, exhibiting a frequency splitting Ω = 24,249±4 Hz. With a quality factor Q = f/Δf≈2×105 and a linewidth of Δf≈40 Hz at the resonance frequency f, the system is clearly in the strong coupling regime of Δf≪Ω. For all measurements discussed in the following, a radiofrequency drive of −59 dBm at 7.539 MHz, resonantly actuating the string at an AWG voltage of 0 V, is applied, which initializes the system in its in-plane mode (Fig. 1c, black circle). A 1 ms long, adiabatic voltage ramp up to 2.82 V brings the state to the point of minimal frequency splitting Ω between the coupled modes. Here, the system dynamics is described by two normal modes, hybrid states formed by the in-phase and out-of-phase combinations of the fundamental flexural modes. The adiabatic ramp thus transforms all the energy of the in-plane mode into the lower hybrid state, such that the classical two-level system2, consisting of the two hybrid modes, is prepared in its lower state. As the drive frequency remains constant (Fig. 1c, dashed line), the string is no longer actuated and its energy is slowly decaying.

Now, the AWG is used to apply a continuous pump tone with frequency Ω to the drive electrodes which starts Rabi oscillations3,11 between the lower and upper state, as shown in Fig. 2. They can be measured directly by monitoring the time evolution of the output power spectrum at the frequency of one of the hybrid modes, here shown for the upper state at 7.6028 MHz, and measured with a bandwidth of 10 kHz. All time-resolved measurements are averaged over 20 (Rabi oscillations and T1 measurement) or 10 pulse sequences (Ramsey fringes and Hahn echo). For a drive amplitude of 100 mV (half peak-to-peak) we find a Rabi frequency of 8.3 kHz (Supplementary Section SIIA). These strong Rabi oscillations demonstrate that the transition between the two hybrid modes forms a classical two-level system, in contrast to the modes themselves, which can be modelled as highly populated harmonic oscillators.

Figure 2: Rabi oscillations.
figure 2

a, Pulse scheme. The system is adiabatically tuned from the initialization to the lower state, then a constant drive with frequency Ω is turned on. b, The z projections of the decaying Rabi oscillations (data coloured dark blue; fit indicated in red) can be directly measured with a spectrum analyser. The Bloch sphere in the inset shows the state of the Bloch vector at selected times, which are marked in the same colour in a.

Full size image

In principle, the decay of these oscillations is governed by both energy relaxation, characterized by a rate 1/T1, and phase decoherence, characterized by 1/T2 or 1/T2*, where T2*≤T2 includes reversible processes caused by slow fluctuations or spatial inhomogeneity of the coupling. For clarity, we use these well-known phenomenological constants in the same way as, for example, in spin systems3, as discussed in detail in Supplementary Section SI.

The exponential decay of a state’s energy defines T1. The corresponding measurement is shown in Fig. 3 for both the lower and upper state: the system is once again prepared in the lower hybrid state. To reach the upper state, a subsequent π-pulse is applied, thus performing one half of a Rabi cycle, which transfers the system to the upper state (Supplementary Section SII for details on the frequency and amplitude calibration of the applied pulses). The exponential decay is then measured directly with a spectrum analyser at a bandwidth of 3 kHz, exhibiting different relaxation times T1,l = 4.83±0.1 ms and T1,u = 4.02±0.1 ms for the lower and upper mode, respectively. They correspond to the spectrally measured quality factors. Previously, it has been shown that, at maximum coupling, the two hybrid modes should have the same quality factor and thus T1 time10. However, both modes are affected by dielectric damping22 (Supplementary Section SIB), leading to the observed difference.

Figure 3: Energy relaxation.
figure 3

a, Pulse scheme. The system is adiabatically tuned from the initialization to the lower state. An additional π-pulse is used to rotate it to the upper state. b, Measured exponential decay of the lower (data shown in green; fit in dark green) and upper (data indicated in blue; fit in dark blue) state. The Bloch sphere in the inset shows the state of the Bloch vector at selected times, which are marked in the same colour in a.

Full size image

To measure the T2* time, a π/2-pulse is used after the preparation in the lower state to bring the system into a superposition state between the lower and upper hybrid modes. The frequency of the pulse is detuned to Ω+500 Hz, leading to a slow precession of the state vector around the z axis of the Bloch sphere3,12. As a result, a second π/2-pulse after time τ does not always bring the system into the upper state, but a slow oscillation, the so-called Ramsey fringes, is observed when the delay τ between the two pulses is varied and the z-projection of the state vector is measured after the second pulse, as shown in Fig. 4. The decay constant of this oscillation is T2*, whereas the decay of the mean value can be interpreted as an effective T1 of both modes. The fit in Fig. 4b results in T2* = 4.44±0.1 ms and T1 = 4.31±0.1 ms. The energy relaxation time of the superposition state T1 is identical to the reciprocal rate average of the two hybrid modes

as the mechanical energy oscillates between the two modes with frequency Ω (Supplementary Movie).

Figure 4: Ramsey fringes.
figure 4

a, Pulse scheme. The system is adiabatically tuned from the initialization to the lower state. A π/2-pulse creates a superposition state, and after a delay τ a second π/2-pulse is applied.b, A 500 Hz detuning between the drive and precession frequency leads to a slow rotation of the superposition state in the equator plane of the Bloch sphere, giving rise to a beating pattern in the measured z component after the second pulse (data shown in dark blue; fit in red). The Bloch sphere in the inset shows the state of the Bloch vector at selected times, which are marked in the same colour in a.

Full size image

By including an additional π-pulse at τ/2 into the Ramsey pulse scheme and replacing the final π/2-pulse by a 3π/2-pulse to once again rotate to the upper state (Fig. 5), the T2 time can be measured in a Hahn echo experiment3,13. The 180°rotation flips the state vector in the x y-plane of the Bloch sphere, thus reversing the effects of a fluctuating or inhomogeneous coupling strength Ω in the second delay interval of τ/2 and thereby cancelling their contribution. The frequency of the pulses is once again exactly Ω, as all three pulses need to be applied exactly around the same axis. The resulting decay curve represents T2, for which a value of T2 = 4.35±0.1 ms can be extracted from the fit in Fig. 5b.

Figure 5: Hahn echo.
figure 5

a, Pulse scheme. The system is adiabatically tuned from the initialization to the lower state. A π/2-pulse creates a superposition state, and after a delay of τ/2 a π-pulse mirrors the state vector to the other half of the Bloch sphere. After another delay of τ/2, a 3π/2-pulse is used to rotate to the upper state. b, The inverse evolution of the system during the two delay times cancels out any broadening or slow precession effects, thus the system always ends up along the z axis and no oscillation is observed (data shown in dark blue; fit in red). The Bloch sphere in the inset shows the state of the Bloch vector at selected times, which are marked in the same colour in a.

Full size image

The good agreement between T2 and T2* clearly shows that reversible elastic dephasing, for example caused by temporal and spatial enviromental fluctuations or spatial inhomogeneities, does not noticeably increase decoherence. The experiment is performed with the two hybrid modes occupied by billions of phonons, making it analogous to a many-spin NMR measurement, only that the macroscopic magnetization is replaced by the mode polarization and a single spin flip corresponds to the transfer of a single phonon between the two modes. But in contrast to the NMR system, here all quasi-particles reside in the same collective mechanical mode and thus experience an identical environment (Supplementary Section SIII).

It is more surprising that the phase coherence time T2 is equal to the average energy relaxation time T1. This indicates the absence of measurable elastic phase relaxation processes in the nanomechanical system, such that the observed loss of coherence is essentially caused by the energy decay of the mechanical oscillation (Supplementary Section SIII). Earlier research20 suggests that the dominant relaxation mechanism in silicon nitride strings is mediated by localized defect states of the amorphous resonator material, described as two-level systems at low temperature. They facilitate energy relaxation by providing the momentum required to transform a resonator phonon into a bulk phonon. For this process to lead to elastic phase relaxation, an excited defect state would have to re-emit the phonon back into the resonator mode, which is extremely unlikely owing to the weak coupling between the two.

In conclusion, we demonstrate coherent electrical control of a strongly coupled (Ω≫f/Q) classical nanomechanical two-level system, employing the pulse techniques well-known from coherent spin dynamics in the field of nanomechanics. Each superposition state of the two hybrid modes on the Bloch sphere can be addressed by a sequence of the described pulses. The presented system stands out by the finding that the elastic phase relaxation rate Γφ is negligible compared with the energy decay rate 2πf/Q, leaving room for improvement of the coherence by means of increased quality factors.

The coherent manipulation schemes presented here allow the simulation of quantum systems using a classical two-level system2. Furthermore, in light of the recent breakthrough in ground-state cooling of nanomechanical resonators23,24,25,26, they can be directly transferred to quantum nanomechanical systems, where they open up new applications in quantum information processing. Not only can they be used as efficient interfaces for quantum state transfers in hybrid quantum systems27,28, but by creating coupled, quantized resonators29 quantum computations can be carried out directly using nanoelectromechanical two-level systems30.