Main

The topological character of topological insulators is determined by the nature of their valence-band wavefunctions, which can be quantified by 4 Z2 invariants. It has been shown that for inversion symmetric crystals it is possible to evaluate these invariants directly with knowledge of the parity of Bloch wavefunctions for the occupied electronic states at high symmetry points in the Brillouin zone7. Although this argument is formulated for inversion symmetric systems, a material’s topological classification does not require inversion or translation symmetry. Therefore, the expectation is that the alloying of known topological insulators with lighter elements by tuning spin–orbit coupling or lattice constant can cause the bulk bandgap Δ to close and invert at a quantum critical point where the topological class changes (Fig. 1a). This has been investigated in the thallium-based ternary chalcogenide alloy TlBi(S1−xSex)2 (refs 8, 9, 10), but thus far only with photoemission (Supplementary Section SB). Although signatures of topological surface state (TSS) conduction have been found in Bi2Se3 (refs 11, 12, 13, 14), a demonstration that the surface transport changes markedly when the bandgap closes and the bulk changes topological class15 would be strong evidence for the topological nature of these materials and is still lacking. In this regard, it was pointed out recently that indium (In) substitutes for bismuth to form a solid solution in Bi2Se3 and that the non-topological endmember In2Se3 of the (Bi1−xInx)2Se3 series shares the common rhombohedral D3d5 structure with Bi2Se3 (ref. 16). In ref. 16, a topological to trivial transition was observed in a range x∼0.03–0.07. In this work, we systematically investigate the details of this topological phase transition.

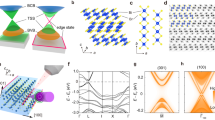
Figure 1: MIR absorption and terahertz sheet conductance of (Bi1−xInx)2Se3 films.
figure 1

a, A schematic of bulk band inversion for the 64 QL series. Valence (conduction) band parity is indicated by the solid green/yellow colour and the plus/minus sign. Spin branches in the non-topological-insulator regime are shifted for clarity. b, Room-temperature MIR absorption (α = ln(1/T)/d, T is transmission and d is film thickness) at 0.31 eV (2,500 cm−1) as a function of In concentration for 32 QL, 64 QL and 128 QL. The error bar derives from the thickness variation in substrates. The curved dashed line is a guide to the eye. The vertical dashed line indicates where the bulk bandgap closes. c, d, Real (c) and imaginary (d) parts of the terahertz sheet conductance of 64 QL (Bi1−xInx)2Se3 films for different In levels at 5 K. e, Experimental data with fits for 64 QL Bi2Se3 at 5 K.

Full size image

Samples investigated in this work were films grown by molecular beam epitaxy. Bi2Se3 films grow in quintuple layer (QL) Se–Bi–Se–Bi–Se blocks. In addition to time-domain terahertz spectroscopy (TDTS), we performed optical absorption measurements in the mid-infrared range, which are sensitive to the energy scale of the bulk bandgap (∼350 meV for Bi2Se3). In Fig. 1b we show that the mid-infrared (MIR) absorption coefficient at 0.31 eV has a distinct peak near x = 0.06 for all of the 32, 64 and 128 QL thicknesses. Despite the fact that even the x = 0 compound has its chemical potential in the bottom of the conduction band, a closing of the bandgap should increase the absorption as the low-energy joint density of states increases. As we will show below, the peak in the MIR absorption with In substitution is consistent with a topological phase transition occurring by closing and reopening of the bandgap at x≈0.06.

In Fig. 1c,d we show the real and imaginary terahertz-range (1 THz = 4.1 meV) conductance of a series of 64 QL (Bi1−xInx)2Se3 films substituted from x = 0 to x = 0.25 at 5 K in the terahertz frequency range. For x = 0 we have previously shown (and will demonstrate again below) that the spectra are characterized by a prominent low-frequency Drude component, which has an almost entirely surface character, and a low-frequency phonon at ∼1.9 THz (ref. 14). With increasing In concentration, the phonon mode broadens and its frequency shifts almost linearly (Supplementary Fig. S4e) to higher frequency owing to the lighter In mass. The Drude peak broadens only slightly up to x = 0.04 in a fashion expected due to the increased disorder. However, for substitutions larger than x = 0.05 the Drude peak broadens markedly and the real part of the conductance becomes flat, indicating that the TSSs have undergone a significant change16. Qualitatively similar results at different doping levels are seen for 16 QL, 32 QL and 128 QL films (Supplementary Section SC). For x≥0.10, the conductance becomes a slowly increasing function of frequency ω consistent with a tendency towards charge localization. The finite conductance of x = 0.10 at low frequency indicates still some metallic behaviour, possibly contributed from the electron pocket seen by photoemission at these substitutions16. The nearly zero conductance of x = 0.17 and x = 0.25 at low frequency and correspondingly the negative slope of the imaginary conductance at low ω indicates insulating behaviour for these concentration levels, which is consistent with the d.c. study16.

To investigate the details of the evolution through the topological quantum phase transition (QPT), we fit the data to a three-component Drude–Lorentz model as shown in Fig. 1e (see Methods and Supplementary Information). Excellent fits are obtained for all data for x<0.08. For the Drude component these fits give a spectral width that can be associated with the transport scattering rate 1/τ and a spectral weight that can be shown to be a function of carrier density. Concentrating again on the 64 QL sample, the Drude scattering rate increases smoothly for low substitutions (Fig. 2a), which is consistent with our above observations and expectation due to increased impurity scattering. However, at x = 0.05 the smooth trend suddenly changes and the scattering rate is enhanced markedly. Just by In substitution alone, we would expect a continued smooth increase of the scattering rate and therefore the sudden change at x = 0.05 in the 64 QL film indicates a transition occurring in the TSSs. We can correlate the sudden changes in the surface transport properties with the MIR absorption peak that is associated with the closing of the bulk bandgap. We conclude that with In substitution a topological phase transition occurs by a closing and reopening of the bandgap at x≈0.06. Therefore, we associate the sudden collapse in the transport lifetime with a loss of topological protection of the surface states on entering the non-topological state. Note that the spectral weight of the Drude component also changes as a function of In substitution (see Supplementary Fig. S4f). The origin of the change is unclear, but may arise in a shift of spectral weight from higher energies or a change in the surface state Fermi velocity.

Figure 2: Finite-size effects and evidence for topological phase transition.
figure 2

a, Scattering rate 1/τ (τ is the transport lifetime) of Drude term from fits as a function of In substitution. The error bar is defined as the parameter range where acceptable fits are obtained. Lines are guides to the eye. The vertical black dashed line indicates where the bulk bandgap closes and band inverts. Inset: A schematic explaining the jump in scattering rate, in which backscattering can occur when surfaces are coupled. b, The scattering rate as a function of thickness at different In concentrations. The dashed lines are fits 1/τ = (A+Be−d/2ξ). ξ is the TSS penetration depth and dis the film thickness in QLs. The 64 QL x = 0.03 point is an interpolation from a. Errors bars represent uncertainties in the fits to the Drude scattering rate. c, Inverse penetration depth 1/ξ as a function of In concentration. The dashed line is a linear fit. Error bars are the uncertainties in the fits in b. Colours refer to the colours denoting concentration levels in b.

Full size image

In general, one expects that the penetration length of the TSS wavefunction is proportional to ℏvF/Δ (refs 17, 18). In the topological regime, 180° backscattering is prohibited owing to spin-momentum locking7. However, 180° backscattering becomes possible when the the bandgap closes sufficiently such that the wavefunction penetration is of the order of half the film thickness, TSSs can hybridize and an electron in a state k with a particular spin can scatter into a state −k with the same spin that derives from the other surface, as shown in the inset of Fig. 2a. One expects that when topological protection is lost in this fashion, the phase space for scattering increases by a factor of the order of unity (Supplementary Section SD), as observed. Our results show directly how the robust transport properties and topological protection of the surface states are dependent on bulk band inversion, but also the essential role of finite-size effects in such transitions.

Looking closer, we note that in fact for the 64 QL sample, we observe the threshold for an increased scattering rate at x = 0.05, and the MIR absorption peaks at x = 0.06. If the surface state’s evanescent length is of the order of a few nanometres at x = 0, a simple estimate based on linearly extrapolating its 0.35 eV bandgap to close at x = 0.06 shows that a 64 QL film should have the threshold for the two TSSs to hybridize and increase scattering shift downward by an amount of the order of x = 0.01 (Supplementary Fig. S3). Reducing the film thickness makes TSSs hybridization occur at even lower In concentration (Supplementary Fig. S3). This dependence on film thickness of the transport lifetime can be seen directly by looking in detail at the fit results in Fig. 2a for 16, 32 and 128 QL series samples. For the same In substitution, thinner samples generally show a more broadened Drude component (Supplementary Section SC). When the film thickness is reduced, the jump in the scattering rate occurs at x = 0.03 and x = 0.04 for the 16 QL and 32 QL series respectively. In contrast, for thicker 128 QL samples, the jump in transport (at x = 0.06) approaches the substitution level where the MIR peak occurs. Therefore, we infer that x≈0.06 is the actual critical concentration where band inversion occurs but the jump in transport occurs at lower concentration in thin samples owing to the finite-size effect.

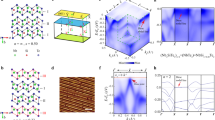
Related physics can be observed by performing thickness-dependent studies. One does not induce a QPT per se, but one can observe the increased phase space due to scattering as surface states overlap. In Fig. 3a–c we show the real and imaginary part of the sheet conductance of pure Bi2Se3 films with different thicknesses. Clearly shown in Fig. 3a,b, the low-frequency Drude component is reasonably thickness independent above 20 QL and broadens appreciably only near 10 QL. The Drude component broadens smoothly below 10 QL and can be resolved well down to 4 QL, whereas the 2 QL sample shows completely different behaviour. We apply the Drude–Lorentz model again to investigate the detailed evolution of the thickness dependence. The 2 QL sample is excluded because no clear Drude peak is observed. As shown in Fig. 3d, the Drude spectral weight is independent of thickness and the phonon spectral weight linearly increases with thickness, which agrees with our previous report14. The Drude scattering rate is enhanced markedly when the film thickness is below 10 QL. As shown in Fig. 2b, the dependence can be well fitted within a Fermi golden rule approach by an exponential function that models the overlap between surfaces 1/τ = (A+Be−d/2ξ), where ξ = 2.7±0.3 QL. This evanescent length agrees well with estimates for the extent of the surface states at x = 0 from angle-resolved photoemission spectroscopy19. Changes in d.c. transport have also been found below these thicknesses and interpreted as the loss of topological protection12,13. We note that the fact that we extract out approximately the same evanescent decay length for the states at EF as for the states near the Dirac point from angle-resolved photoemission spectroscopy is a particularity of the topological surface band structure. As long as one considers high-symmetry surfaces the decay length can be shown to be independent of energy for all energies below the conduction band threshold18 (F. Zhang and E. J. Mele, personal communication (2013); Supplementary Section SA for further information).

Figure 3: Crossover from 3D topological insulator to 2D topological insulator in pure Bi2Se3.
figure 3

a–c, Real (a,b) and imaginary (c) sheet conductance of pure Bi2Se3 films with different thicknesses at 5 K. d, 2D Drude spectral weight ((ωp/2π)2d) and 2D phonon spectral weight (4(ωp−phonon/2π)2d) as a function of film thickness. e, A schematic showing how TSS hybridization occurs when the film thickness is reduced. 4 QL and 2 QL films may be topologically non-trivial and trivial respectively as proposed in refs 20, 21. Spin-up and spin-down branches in the non-topological-insulator regime are shifted for clarity. f, A phase diagram constructed to distinguish different phases. Solid markers with different shapes correspond to data in different regimes. The boundary between the topological insulator (TI) and the hybridized regime is set by the length scales determined by the fits in Fig. 2b.

Full size image

One can apply the scaling analysis as a function of thickness (Fig. 2b) to extract out the relevant length scale for the In-substituted samples. The advantage of performing this scaling as a function of thickness is that a sample’s disorder level remains constant. In each of these fits we constrain the constant offset A to be the value of the scattering rate of the thickest sample. Showing a remarkable consistency in our treatment, one can see from Fig. 2c that the inverse length scale extrapolates linearly to zero at the substitution level of the QPT at x≈0.06 in a fashion expected for a correlation length near a continuous transition.

It is interesting to note the pronounced difference in spectra between 2 QL and 4 QL x = 0 samples. An oscillatory behaviour between two-dimensional (2D) topological non-trivial and trivial behaviour as a function of thickness has been theoretically proposed20,21, as shown schematically in Fig. 3e. The large differences we observe could be related to such a phase transition. Nevertheless, one must be careful here as surface steps with 1 QL depth and oxidization are very important in the 2 QL sample and, therefore, it is impossible to make a strong conclusion (see further discussion in Supplementary Section SG).

The large number of samples we have measured and the thickness-dependent fits allow us to map out a detailed phase diagram as a function of thickness and concentration that includes regions of a 3D topological insulator, a 3D non topological insulator and a regime we call hybridized topological insulator, by which we mean the bulk bands are still inverted but surface states hybridize. As shown in Fig. 3f the threshold for increased scattering starts near 5 QL (the point at which surface states penetrating ≈2.5 QL first overlap) and asymptotically approaches the boundary where the true phase transition occurs in a thermodynamically large sample. Note that increased scattering can be resolved even for films thicker than this threshold as there is an exponential tail to the wavefunctions involved.

In the non-topological phase an even number of spin species must exist on a surface as opposed to the topological phase where an odd number of spin species exist. Our work demonstrates where the other spin species comes from when a system crosses the QPT. It comes from the other surface. Our work also shows the non-trivial effects that the finite size of a sample has on a QPT as a consequence of the bulk-boundary correspondence-derived properties of the TSS. Here the role of the correlation length associated with the QPT is played by the evanescent decay length of the TSS. It would be interesting to investigate these effects even asymptotically closer to the transition. We also hope this work can generate further interest in the field of topological phase transitions, particularly in guiding first-principles calculations for In substitution in Bi2Se3 to reveal the evolution of the band structure. Our work will also facilitate applications based on topological insulator systems where the bandgap has been tuned by substitution to a particular photonic band. Our results show the intrinsic limitations on devices (and their fabrication) made for such purposes.

Methods

The high-quality epitaxial (Bi1−xInx)2Se3 thin films were prepared by molecular beam epitaxy using the two-step growth recipe developed at Rutgers University13,22. An initial deposition of 3 QL was made at 110 °C, which was followed by annealing to 220 °C, where the remaining deposition was performed to achieve the desired thickness. Reflection high-energy electron diffraction was used to monitor the film quality during growth; the results indicate that the films are high-quality single phase even when made as thin as 2 QL (refs 13, 16). The films were deposited in an excess Se flux, such that the flux ratio of Se to the combined Bi and In flux was kept at ∼ 10/1. Control of the Bi and In flux was critical to achieve the desired concentration and thickness. The Bi and In cells were calibrated in situ by a quartz crystal microbalance, and ex situ by Rutherford backscattering. Together these provide accuracy to within about 1% of the targeted concentration. The precise substitution level can be confirmed as the low-frequency infrared-active phonon moves strongly to higher frequencies in a linear fashion with substitution of In (Supplementary Fig. S4f). Samples were sealed in vacuum and sent immediately to Johns Hopkins University.

Standard TDTS in a transmission geometry was performed with a custom home-built terahertz spectrometer. In this technique an almost single-cycle one picosecond pulse of electromagnetic radiation is transmitted through the sample. The complex transmission function that results from Fourier transforming the pulse and ratioing it to a Fourier transformed reference pulse can be directly inverted to give the complex conductance G(ω) in the thin-film limit: , where Φs is the phase accumulated from the small difference in thickness between the sample and reference substrates and n is the substrate index of refraction. By measuring both the magnitude and phase of the transmission, this inversion to conductance is done directly and does not require Kramers–Kronig transformation. TDTS turns out to be an ideal probe of the low-frequency response of topological insulator materials with both the metallic Drude transport peak and the phonon peak observable in the experimental range. Low-temperatures TDTS measurements generally began within 24 h of their growth. The total exposure time to atmosphere was less than 30 min. The samples were mounted inside an optical helium flow cryostat and cooled down to 5 K within an hour. Transmission measurements in the MIR region were performed with a Fourier transform infrared spectrometer (Bruker Vertex 80) at room temperature in vacuum.

The data are fitted by a Drude–Lorentz model by using the RefFIT program23. We include only a single Drude term (a Lorentzian centred at ω = 0), a Drude–Lorentz term (which models the phonon) and a frequency-independent real contribution to the dielectric constant (which accounts for the effect of higher-energy excitations on the low-frequency physics)14,24:

where d is the film thickness (further discussion in Supplementary Section SF).