Abstract
Electrons can be accelerated to ultrarelativistic energies at strong (high Mach number) collisionless shock waves that form when stellar debris rapidly expands after a supernova1,2,3. Collisionless shock waves also form in the flow of particles from the Sun (the solar wind), and extensive spacecraft observations have established that electron acceleration at these shocks is effectively absent whenever the upstream magnetic field is roughly parallel to the shock-surface normal (quasi-parallel conditions)4,5,6,7,8. However, it is unclear whether this magnetic dependence of electron acceleration also applies to the far stronger shocks around young supernova remnants, where local magnetic conditions are poorly understood. Here we present Cassini spacecraft observations of an unusually strong solar system shock wave (Saturn’s bow shock) where significant local electron acceleration has been confirmed under quasi-parallel magnetic conditions for the first time, contradicting the established magnetic dependence of electron acceleration at solar system shocks4,5,6,7,8. Furthermore, the acceleration led to electrons at relativistic energies (about megaelectronvolt), comparable to the highest energies ever attributed to shock acceleration in the solar wind4. These observations suggest that at high Mach numbers, such as those of young supernova remnant shocks, quasi-parallel shocks become considerably more effective electron accelerators.
Similar content being viewed by others
Main
Shock waves form when flow relative to an obstacle is greater than the speed of information transfer through the medium. Flow kinetic energy is dissipated at a shock, and fluid properties change abruptly, producing a slower downstream flow that is able to avoid the obstacle. In collisional fluids (such as Earth’s atmosphere) energy dissipation at a shock wave occurs through inter-particle collisions; however, in effectively collisionless (highly tenuous) media, such as charged particle (plasma) space environments, dissipation at shocks is through particle–electromagnetic field interactions9. The fraction of flow kinetic energy dissipated at a shock is indicated by the shock Mach numbers (flow speed divided by upstream wave speeds). Particle motion at the shock is controlled by the shock angle (θB n), the angle between the shock normal and the upstream magnetic field vector, which defines two categories of collisionless shock: quasi-parallel (0°<θBn<45°) and quasi-perpendicular (45°<θBn<90°). Energy dissipation at a collisionless shock not only leads to heating of the bulk plasma, but can also accelerate some particles to much higher energies.
It is widely believed that a major fraction of the energetic charged particles that pervade the Galaxy (cosmic rays with energies up to ∼1015 eV) are accelerated at collisionless shock waves associated with supernova explosions1. The specific acceleration mechanism typically invoked in this context, commonly referred to as diffusive shock acceleration, is thought to result from a Fermi process where particles bounce between converging scattering centres (for example, electromagnetic waves) located on either side of the shock1. Emissions associated with ultrarelativistic electrons produced at young (<1,000-year-old) supernova remnant shocks have been comprehensively studied using both Earth-based and space-based telescopes2,3,10. However, poorly constrained local conditions at these exotic, distant shocks11, and in particular the hardly known magnetic field conditions lead to uncertainty surrounding the electron acceleration process.
Observations made by spacecraft during encounters with collisionless shocks in the Solar System can potentially shed light on the physics of these supernova remnant shocks9. Shocks are common in the solar-wind plasma that flows away from the Sun and carries the solar magnetic field into interplanetary space12,13. Electron acceleration is often observed, although not to the ultrarelativistic (teraelectronvolt–petaelectronvolt) energies produced at young supernova remnant shocks, and various acceleration mechanisms have been discussed. Observed electron acceleration is significantly more efficient at quasi-perpendicular shocks than at quasi-parallel shocks4,5,6,7,8, although even under quasi-perpendicular conditions the detection of relativistic (megaelectronvolt) electrons is rare4. As solar system shocks are generally far weaker (lower Mach number) than their young supernova remnant counterparts, and also far smaller, it is unclear whether the observed magnetic dependence of electron acceleration also applies to much stronger shocks. Limited observations, and theoretical predictions, suggest that quasi-parallel shocks may become efficient electron accelerators at high Mach numbers5,14,15.
Here we present in situ spacecraft observations of an unusually strong quasi-parallel shock wave. NASA’s Cassini spacecraft has made hundreds of crossings of the shock that stands in the solar wind in front of Saturn (the planetary bow shock) owing to the obstacle presented by the planet’s intrinsic magnetic field (the planetary magnetosphere)16,17,18. A set of 94 Cassini crossings of Saturn’s bow shock have been analysed in a previous study, resulting in an Alfvén Mach number (MA, related to the upstream speed of Alfvén waves) for each18. The highest MA case (∼ 100) is presented here, and is the only quasi-parallel crossing associated with strong evidence for shock acceleration of solar-wind electrons. The significantly higher value of MA than other quasi-parallel crossings (second highest: MA∼40) suggests that this electron acceleration resulted from the unusually high Mach number14,15. The upstream electron β was also relatively high (∼ 10, the ratio of electron to magnetic pressures); however, unlike MA, it was not clearly the highest (considering uncertainties)18.
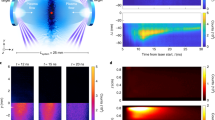
A schematic illustrating Cassini’s encounter with Saturn’s bow shock under this combination of quasi-parallel and high-Mach-number conditions is shown in Fig. 1. The crossing took place at ∼ 1:10 Universal Time (UT) on 3 February 2007, when the spacecraft was close to the subsolar point on the shock surface (the point closest to the magnetospheric obstacle, where the Mach numbers are expected to be highest). In situ observations made by Cassini between 0:00 and 2:00 UT are shown in Fig. 2. Under these quasi-parallel magnetic conditions a collisionless shock is a broad and complex transition between upstream and downstream plasma states19,20, and the observations presented in Fig. 2 are consistent with this expectation. The spacecraft began the interval upstream, observed the major heating and compression of thermal plasma during a roughly 10-min-long interval centred on ∼ 1:10 UT (Fig. 2f,h), and ended the interval downstream (Fig. 1).
(Not to scale.) In Kronocentric Solar Magnetospheric (KSM) coordinates (origin at the centre of the planet, x axis pointing towards the Sun, z axis defining an x–z plane containing Saturn’s magnetic dipole axis, y axis completing the right-handed Cartesian set) the spacecraft location at the time of the shock crossing was (x, y, z)∼(17, 4, −3), in units of Saturn radii (RS). The increasing grey shading from left to right in the zoom-in view of the region where the shock was encountered indicates the increase in thermal plasma density across the shock. The simplest possible spacecraft trajectory in the shock rest frame is shown.
a, Magnetic field magnitude on both linear and logarithmic scales24. b, Magnetic field elevation angle, the angle between the field and the x–y KSM plane (positive/negative for positive/negative z component). c, Magnetic field azimuthal angle, the anticlockwise angle of the projection of the field onto the x–y KSM plane (the positive x axis is at 0°, the positive y axis is at 90°, the negative x axis is at 180/−180° and the negative y axis is at −90°). d, Frequency–time spectrogram of electric field power spectral density25 (PSD). The electron gyrofrequency is over-plotted in black, and estimates of the upstream electron plasma frequency and measurements of the downstream electron plasma frequency are over-plotted as dashed white lines. e,f, Energy–time spectrograms of electron differential intensity (DI) from the LEMMS of the Cassini magnetospheric imaging instrument22, and anode 5 of the ELS of the Cassini plasma spectrometer21, respectively. The ELS energy range has been restricted to <18 keV. Vertical dashed lines indicate sub-intervals relevant for Fig. 3. g, Normalized electron differential intensity in three energy ranges. Only data above the ELS one-count level are shown for the 5–10 keV range. h, Energy–time spectrogram of ion differential energy flux21 (DEF).
The weak magnetic field strength upstream of this shock encounter (∼ 0.1 nT, Fig. 2a) was primarily responsible for the calculation of MA∼100, which is very high for a solar system shock18. Using typical electron and ion temperatures in the near-Saturn solar wind16 we estimate both the sonic and fast magnetosonic Mach numbers as ∼ 25. Before ∼ 0:05 UT the spacecraft was not magnetically connected to Saturn’s bow shock, and the steady magnetic field orientation suggests that the shock (located planetward of the spacecraft) was quasi-perpendicular at this time (θBn∼60°, using a shock normal predicted by a model17). At ∼ 0:05 UT the field orientation changed, magnetically connecting the spacecraft to a region of the shock surface that was quasi-parallel. From this time the spacecraft was located in a region of space where shock-reflected ions moved back upstream along magnetic field lines, and interacted with the incoming solar-wind ion population to produce strong magnetic field fluctuations (Fig. 2a–c) and a population of so-called diffuse ions (Fig. 2h, population at ∼ 10 keV observed before ∼ 1:00 UT)19,20. Time-averaging the upstream (before ∼ 1:00 UT) magnetic field to resolve the nominal field from the field fluctuations (using a range of sufficiently long averaging intervals) suggests θBn∼20°. After the main thermal plasma shock transition (centred on ∼ 1:10 UT) the spacecraft sampled the downstream region, where the magnetic field was stronger (Fig. 2a) and the thermal plasma was hotter and denser (Fig. 2f,h). Cassini intermittently observed emissions above the electron gyrofrequency during the interval (Fig. 2d).
As the purpose of this letter is to present evidence for electron acceleration at the shock, Cassini electron data sets are primarily discussed here. The electron spectrometer (ELS) of the Cassini plasma spectrometer21 detects electrons below 27 keV. The low-energy magnetospheric measurements system (LEMMS) of the Cassini magnetospheric imaging instrument22 detects electrons above 18 keV. As all ELS anodes measured intensities at the one-count level above 18 keV throughout the interval, ELS energy spectra are restricted to below 18 keV (the lower limit of the LEMMS energy range). The combination of the variability of the magnetic field orientation during this 2 h interval (Fig. 2b,c), the pointing of the relevant instruments21,22, and the orientation of the spacecraft prevent the resolution of any anisotropies in the electron distribution, for example related to particle pitch angles. To compare electron distributions upstream, during the thermal plasma transition, and downstream, Fig. 3 shows combined ELS–LEMMS electron energy spectra, time-averaged over different 2-min-long intervals (indicated in Fig. 2e,f). Note that the dashed black lines give the ELS one-count level, and LEMMS intensities are background-subtracted, with no data shown when a LEMMS energy channel was at the background level. As these two instruments are not inter-calibrated we expect an offset in intensity at 18 keV, and it is not appropriate to compare the ELS and LEMMS spectral slope at 18 keV unless ELS intensities were significantly above the one-count level. Figure 4 shows a comparison of the LEMMS spectra alone.
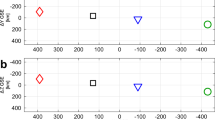
In all panels the vertical dashed line separates data taken by the ELS and LEMMS instruments. Dashed curves give the ELS one-count level and dotted curves show Maxwellian distributions for comparison. a, The single peak in the ELS data is a mixture of solar-wind electrons and spacecraft photoelectrons (which result from photons hitting the metallic surfaces of the spacecraft). b,c, The two peaks in the ELS data indicate the separation of these populations (where the spacecraft photoelectron population is less energetic). Grey rectangles indicate the energy range of each LEMMS channel. LEMMS data have been background-subtracted, and no data point in an energy channel indicates intensity at the background level. The lack of inter-calibration between the instruments produces an offset in differential intensity at 18 keV, which we do not attempt to address because ELS was not significantly above the one-count level at 18 keV at any point during the encounter. Error bars are standard deviations for each sub-interval.
The LEMMS data reveal an electron population above background up to ∼ 100 keV from when the spacecraft became magnetically connected to the shock at ∼ 0:05 UT (Figs 2e and 3a). This population seems to have been present both upstream and downstream of the shock (Figs 2e, 3a,c and 4), and has a similar spectral shape to the (higher intensity) spectrum measured immediately inside Saturn’s magnetosphere less than an hour earlier (Fig. 4). We identify this population as electrons escaping from Saturn’s magnetosphere, where they were already at similar energies23. The observation of magnetospheric particle escape requires a magnetic connection to the bow shock23, consistent with the detection of this population from ∼ 0:05 UT onwards.
The main thermal plasma transition (centred on ∼ 1:10 UT) was the only occasion when ELS measured intensities above the one-count level between 5 and 10 keV (Figs 2g and 3b). This is clear evidence for the shock acceleration of solar-wind electrons, which is a well-observed phenomenon at (weaker) quasi-perpendicular shocks5,8. Coincident with the peak of this signal seen by ELS, all LEMMS energy channels were above background (including the highest, which approaches megaelectronvolt energies), and all recorded peak intensities (Figs 2g and 4). Intensities in the ≲100 keV energy channels were significantly (at least ∼ 10 times) higher than those associated with the leaking magnetospheric electron population measured upstream and downstream, and produced a different spectral shape (Fig. 4). Intensities in the ≳100 keV channels revealed a flatter spectrum at these higher energies. This LEMMS signal was detected over a longer time interval than the associated ELS signal (Fig. 2e,g).
We identify this combined electron signature as the first in situ evidence for significant acceleration of solar-wind electrons (to relativistic energies) at a quasi-parallel shock wave. Leaking magnetospheric electrons may have been a further seed population for shock acceleration. However, the relatively low intensity of the leaking population, the change in the ≲100 keV spectral slope at the shock transition (where thermal solar-wind electrons were efficiently accelerated) and the similarity between the leaking population measured upstream and downstream all indicate that solar-wind electrons were the dominant seed population (Fig. 4). The electron dynamics at this shock encounter remains to be fully understood. The change in spectral shape at ∼ 100 keV present in the LEMMS spectrum at the shock transition suggests the operation of more than one acceleration mechanism (Fig. 4). We note that the intensity of the shock-accelerated electrons detected by LEMMS does not remain constant downstream, as predicted by simple one-dimensional diffusive shock acceleration theory, and such differences must be explained by any proposed model of electron acceleration and transport.
References
Blandford, R. & Eichler, D. Particle acceleration at astrophysical shocks: A theory of cosmic ray origin. Phys. Rep. 154, 1–75 (1987).
Aharonian, F. A. et al. High-energy particle acceleration in the shell of a supernova remnant. Nature 432, 75–77 (2004).
Uchiyama, Y., Aharonian, F. A., Tanaka, T., Takahashi, T. & Maeda, Y. Extremely fast acceleration of cosmic rays in a supernova remnant. Nature 449, 576–578 (2007).
Sarris, E. T. & Krimigis, S. M. Quasi-perpendicular shock acceleration of ions to ∼ 200 MeV and electrons to ∼ 2 MeV observed by Voyager 2. Astrophys. J. 298, 676–683 (1985).
Gosling, J. T., Thomsen, M. F., Bame, S. J. & Russell, C. T. Suprathermal electrons at Earth’s bow shock. J. Geophys. Res. 94, 10011–10025 (1989).
Krimigis, S. M. Voyager energetic particle observations at interplanetary shocks and upstream of planetary bow shocks: 1977–1990. Space Sci. Rev. 59, 167–201 (1992).
Shimada, N. et al. Diffusive shock acceleration of electrons at an interplanetary shock observed on 21 Feb 1994. Astro. Space Sci. 264, 481–488 (1999).
Oka, M. et al. Whistler critical Mach number and electron acceleration at the bow shock: Geotail observation. Geophys. Res. Lett. 33, L24104 (2006).
Treumann, R. A. Fundamentals of collisionless shocks for astrophysical application, 1. Non-relativistic shocks. Astron. Astrophys. Rev. 17, 409–535 (2009).
Reynolds, S. P. Supernova remnants at high energy. Annu. Rev. Astron. Astrophys. 46, 89–126 (2008).
Vink, J. Supernova remnants: The X-ray perspective. Astron. Astrophys. Rev. 20, 49–168 (2012).
Smith, E. J. in Collisionless Shocks in the Heliosphere: Reviews of Current Research (eds Tsurutani, B. T. & Stone, R. G.) 69–83 (Geophysical Monograph Series 35, American Geophysical Union, 1985).
Russell, C. T. in Collisionless Shocks in the Heliosphere: Reviews of Current Research (eds Tsurutani, B. T. & Stone, R. G.) 109–130 (Geophysical Monograph Series 35, American Geophysical Union, 1985).
Levinson, A. Electron injection in collisionless shocks. Astrphys. J. 401, 73–80 (1992).
Amano, T. & Hoshino, M. A critical Mach number for electron injection in collisionless shocks. Phys. Rev. Lett. 104, 181102 (2010).
Achilleos, N. et al. Orientation, location, and velocity of Saturn’s bow shock: Initial results from the Cassini spacecraft. J. Geophys. Res. 111, A03201 (2006).
Went, D. R., Hospodarsky, G. B., Masters, A., Hansen, K. C. & Dougherty, M. K. A new semiempirical model of Saturn’s bow shock based on propagated solar wind parameters. J. Geophys. Res. 116, A07202 (2011).
Masters, A. et al. Electron heating at Saturn’s bow shock. J. Geophys. Res. 116, A10107 (2011).
Eastwood, J. P. et al. The foreshock. Space Sci. Rev. 118, 41–94 (2005).
Burgess, D. et al. Quasi-parallel shock structure and processes. Space Sci. Rev. 118, 205–222 (2005).
Young, D. T. et al. Cassini plasma spectrometer investigation. Space Sci. Rev. 114, 1–112 (2004).
Krimigis, S. M. et al. Magnetosphere imaging instrument (MIMI) on the Cassini mission to Saturn/Titan. Space Sci. Rev. 114, 233–329 (2004).
Krimigis, S. M. et al. Analysis of a sequence of energetic ion and magnetic field events upstream from the Saturnian magnetosphere. Planet. Space Sci. 57, 1785–1794 (2009).
Dougherty, M. K. et al. The Cassini magnetic field investigation. Space Sci. Rev. 114, 331–383 (2004).
Gurnett, D. A. et al. The Cassini radio and plasma wave investigation. Space Sci. Rev. 114, 395–463 (2004).
Acknowledgements
A.M. acknowledges the support of the JAXA International Top Young Fellowship Program, and P. Gandhi for useful discussions. We thank Cassini instrument Principal Investigators D. A. Gurnett, S. M. Krimigis and D. T. Young. This work was supported by UK STFC through rolling grants to MSSL/UCL and Imperial College London.
Author information
Authors and Affiliations
Contributions
A.M. identified the event, analysed the combined data set, proposed the interpretation and wrote the paper. L.S., M.F., S.J.S., H.H. and B.Z. discussed the interpretation. N.S., M.F.T., A.R. and G.R.L. each analysed, and checked the interpretation of, one data set. A.J.C., P.C. and M.K.D. oversaw the data analysis and interpretation. All authors reviewed the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
About this article
Cite this article
Masters, A., Stawarz, L., Fujimoto, M. et al. Electron acceleration to relativistic energies at a strong quasi-parallel shock wave. Nature Phys 9, 164–167 (2013). https://doi.org/10.1038/nphys2541
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys2541
This article is cited by
-
Magnetosheath jets at Jupiter and across the solar system
Nature Communications (2024)
-
Downstream high-speed plasma jet generation as a direct consequence of shock reformation
Nature Communications (2022)
-
Nonthermal electron acceleration at collisionless quasi-perpendicular shocks
Reviews of Modern Plasma Physics (2022)
-
Electron acceleration by wave turbulence in a magnetized plasma
Nature Physics (2018)
-
Jets Downstream of Collisionless Shocks
Space Science Reviews (2018)