Abstract
The experimental violation of Bell inequalities using space-like separated measurements precludes the explanation of quantum correlations through causal influences propagating at subluminal speed1,2. Yet, any such experimental violation could always be explained in principle through models based on hidden influences propagating at a finite speed v>c, provided v is large enough3,4. Here, we show that for any finite speed v with  , such models predict correlations that can be exploited for faster-than-light communication. This superluminal communication does not require access to any hidden physical quantities, but only the manipulation of measurement devices at the level of our present-day description of quantum experiments. Hence, assuming the impossibility of using non-local correlations for superluminal communication, we exclude any possible explanation of quantum correlations in terms of influences propagating at any finite speed. Our result uncovers a new aspect of the complex relationship between multipartite quantum non-locality and the impossibility of signalling.
, such models predict correlations that can be exploited for faster-than-light communication. This superluminal communication does not require access to any hidden physical quantities, but only the manipulation of measurement devices at the level of our present-day description of quantum experiments. Hence, assuming the impossibility of using non-local correlations for superluminal communication, we exclude any possible explanation of quantum correlations in terms of influences propagating at any finite speed. Our result uncovers a new aspect of the complex relationship between multipartite quantum non-locality and the impossibility of signalling.
Similar content being viewed by others
Main
Correlations cry out for explanation1. Our intuitive understanding of correlations between events relies on the concept of causal influences, either relating directly the events, such as the position of the moon causing the tides, or involving a past common cause, such as seeing a flash and hearing the thunder when a lightning strikes. Importantly, we expect the chain of causal relations to satisfy a principle of continuity, that is, the idea that the physical carriers of causal influences propagate continuously through space at a finite speed. Given the theory of relativity, we expect moreover the speed of causal influences to be bounded by the speed of light. The correlations observed in certain quantum experiments call into question this viewpoint.
When measurements are performed on two entangled quantum particles separated far apart from each other, such as in an Einstein–Podolsky–Rosen5 type experiment, the measurement results of one particle are found to be correlated to that of the other particle. Bell showed that if these correlated values were due to past common causes, then they would necessarily satisfy a series of inequalities1. However, theory predicts and experiments confirm that these inequalities are violated2, thus excluding any past common cause type of explanation. Moreover, as the measurement events can be space-like separated6,7,8, any influence-type explanation must involve superluminal influences9, in contradiction with the intuitive notion of relativistic causality10.
This non-local connection between distant particles represents a source of tension between quantum theory and relativity10,11; however, it does not put the two theories in direct conflict owing to the no-signalling property of quantum correlations. This property guarantees that spatially separated observers in an Einstein, Podolsky and Rosen-type experiment cannot use their measurement choices and outcomes to communicate with one another. The complex relationship between quantum non-locality and relativity has been the subject of intense scrutiny9,10,11,12, but less attention has been paid to the fact that quantum non-locality seems to invalidate not only the intuitive notion of relativistic causality, but more fundamentally the idea that correlations can be explained by causal influences propagating continuously in space. Indeed, according to the standard textbook description, quantum correlations between distant particles, and hence the violation of Bell inequalities, can in principle be achieved instantaneously and independently of the spatial separation between the particles. Any explanation of quantum correlations using hypothetical influences would therefore require that they propagate at speed  , that is jump instantaneously from one location to another as in real actions at a distance.
, that is jump instantaneously from one location to another as in real actions at a distance.
Is such an infinite speed a necessary ingredient to account for the correlations observed in nature or could a finite speed v, recovering a principle of continuity, be sufficient? In particular, could an underlying theory with a limit v on the speed of causal influences reproduce correctly the quantum predictions, at least when distant quantum systems are within the range of finite-speed causal influences13? Obviously, any such theory would cease to violate Bell inequalities beyond some range determined by the finite speed v. At first, this hypothesis seems untestable. Indeed, provided that v is large enough, any model based on finite-speed (hidden) influences can always be made compatible with all experimental results observed so far. It thus seems as if the best that one could hope for is to put lower bounds on v by testing the violation of Bell inequalities with systems that are further apart and better synchronized3,4.
Here we show that there is a fundamental reason why influences propagating at a finite speed v may not account for the non-locality of quantum theory: all such models give, for any v>c, predictions that can be used for faster-than-light communication. Importantly, our argument does not require the observation of non-local correlations between simultaneous or arbitrarily distant events and is thus amenable to experimental tests. Our results answer a long-standing question on the plausibility of finite-speed models first raised in refs 14, 15. Progress on this problem was recently made in ref. 16, where a conclusion with a similar flavour was obtained, but not for quantum theory. Technically, our approach is independent and different from the one in ref. 16, which relies on transitivity of non-locality, a concept that has not yet found any application in quantum theory.
We derive our results assuming that the speed of causal influences v is defined with respect to a privileged reference frame (or a particular foliation of spacetime into space-like hyperplanes). It should be stressed that although the assumption of a privileged frame is not in line with the spirit of relativity, there is also no empirical evidence implying its absence. In fact, even in a perfectly Lorentz-invariant theory, there can be natural preferred frames owing to the non-Lorentz-invariant distribution of matter—a well-known example of this is the reference frame in which the cosmic microwave background radiation seems to be isotropic (see, for example, ref. 17). Moreover, note that there do exist physical theories that assume a privileged reference frame and are compatible with all observed data, such as Bohmian mechanics18,19, the collapse theory of Ghirardi, Rimini and Weber20 and its relativistic generalization21. Although both of these theories reproduce all tested (non-relativistic) quantum predictions, they violate the principle of continuity mentioned above (otherwise they would not be compatible with no-signalling as our result implies).
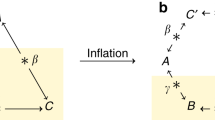
The models that we consider, which we call v-causal models, associate with each spacetime point K a past and a future v-cone in the privileged frame, generalizing the notion of past and future light cones, see Fig. 1. An event at K1 can have a causal influence on a point K2>K1 located in its future v-cone and can be influenced by a point K3<K1 in its past v-cone. However, there cannot be any direct causal relation between two events K1∼K4 that are outside each other’s v-cones. The causal structure that we consider here thus corresponds to Bell’s notion of local causality9,22 but with the speed of light c replaced by the speed v>c. Operationally, it is useful to think of the correlations generated by v-causal models as those that can be obtained by classical observers using shared randomness together with communication at speed v>c.
In the (shaded) light cone delimited by solid lines, causal influences propagate up to the speed of light c, whereas in the v-cone (hatched region), causal influences travel up to the speed v. An event K1 can causally influence a space-like separated event K2 contained in its future v-cone and can be influenced by an event K3 that lies in its past v-cone, but it cannot directly influence or be influenced by event K4 outside its v-cone.
According to the textbook description of quantum theory, local measurements on composite systems prepared in a given quantum state ρ yield the same joint probabilities regardless of the spacetime ordering of the measurements. However, a v-causal model will generally not be able to reproduce these quantum correlations when the spacetime ordering does not allow influences to be exchanged between certain pairs of events. In particular, the correlations between A and B will never violate Bell inequalities when A∼B (see Fig. 2). A possible programme to rule out v-causal models thus consists of experimentally observing Bell violations between pairs of measurement events as simultaneous as possible in the privileged reference frame3. As pointed out earlier, however, this programme can at best lower bound the speed v of the causal influences.
We denote by P(a b|x y) the probability associated with A and B observing respectively the outcomes a and b when their measurement is labelled by x and y. In quantum theory, such probabilities are given by  , where ρ is the quantum state of A and B and Max, Mby their respective measurement operators, and are independent of the spacetime ordering of the measurements. In contrast, in a v-causal model, the observed probabilities will depend on the spacetime ordering between A and B, as we now specify. a, A is in the past v-cone of B. Let the variable λ, with probability distribution q(λ), denote the joint state of the particles, or more generally a complete specification of any initial information in the shaded spacetime region that is relevant to make predictions about a and b (strictly, only the shaded region that is in the past v-cone of A can have a causal influence on A; however, all of our arguments still follow through even if we consider spacetime regions of the kind depicted). In this situation we can write
, where ρ is the quantum state of A and B and Max, Mby their respective measurement operators, and are independent of the spacetime ordering of the measurements. In contrast, in a v-causal model, the observed probabilities will depend on the spacetime ordering between A and B, as we now specify. a, A is in the past v-cone of B. Let the variable λ, with probability distribution q(λ), denote the joint state of the particles, or more generally a complete specification of any initial information in the shaded spacetime region that is relevant to make predictions about a and b (strictly, only the shaded region that is in the past v-cone of A can have a causal influence on A; however, all of our arguments still follow through even if we consider spacetime regions of the kind depicted). In this situation we can write  , where we used Bayes’ rule in the second equality and the assumption that the measurement setting y is a free variable, that is, uncorrelated to a,x,λ, in the last equality. Note that there always exists a trivial v-causal model that reproduces the quantum correlations in the case A<B (or B<A) as we can write PQ(a b|x y) = PQ(a|x)PQ(b|y,a x) by the no-signalling property of quantum correlations (this easily generalizes to the multipartite case, see Supplementary Information SA). b, A and B are outside each other’s v-cones. As above, the variable λ represents a complete (as far as predictions about a and b are concerned) specification of the shaded spacetime region. Note that this region screens-off the intersection of the past v-cones of A and B, in the sense that given the specification of λ in the shaded region, specification of any other information in the past v-cones of A and B becomes redundant. It thus follows that P(a|x,b y λ) = P(a|x,λ) because any information about B is irrelevant to make predictions about a once λ is specified (see ref. 9 for a more detailed discussion of this condition). Similarly, P(b|y,a x λ) = P(b|y,λ). We can therefore write
, where we used Bayes’ rule in the second equality and the assumption that the measurement setting y is a free variable, that is, uncorrelated to a,x,λ, in the last equality. Note that there always exists a trivial v-causal model that reproduces the quantum correlations in the case A<B (or B<A) as we can write PQ(a b|x y) = PQ(a|x)PQ(b|y,a x) by the no-signalling property of quantum correlations (this easily generalizes to the multipartite case, see Supplementary Information SA). b, A and B are outside each other’s v-cones. As above, the variable λ represents a complete (as far as predictions about a and b are concerned) specification of the shaded spacetime region. Note that this region screens-off the intersection of the past v-cones of A and B, in the sense that given the specification of λ in the shaded region, specification of any other information in the past v-cones of A and B becomes redundant. It thus follows that P(a|x,b y λ) = P(a|x,λ) because any information about B is irrelevant to make predictions about a once λ is specified (see ref. 9 for a more detailed discussion of this condition). Similarly, P(b|y,a x λ) = P(b|y,λ). We can therefore write  . Formally, the correlations are thus local and satisfy all Bell inequalities. In particular, the model cannot reproduce arbitrary quantum correlations in this situation.
. Formally, the correlations are thus local and satisfy all Bell inequalities. In particular, the model cannot reproduce arbitrary quantum correlations in this situation.
More fundamentally, one could ask whether it is even possible to conceive a v-causal model that reproduces the quantum correlations in the favourable situation where all successive measurement events are causally related by v-speed signals, that is, when any given measured system can freely influence all subsequent ones? In the bipartite case, this is always possible (see Fig. 2 and Supplementary Information SA), and thus the only possibility is to lower bound v experimentally. In the four-partite case, however, we show below that any v-causal model of this sort necessarily leads to the possibility of superluminal communication, independently of the (finite) value of v. Importantly, the argument does not rely directly on the observation of non-local correlations between simultaneous events.
Let us stress that v-causal models evidently allow for superluminal influences at the hidden, microscopic level, provided that they occur at most at speed v. Such superluminal influences, however, need not a priori be manifested in the form of signalling at the macroscopic level, that is at the level of the experimenters who have no access to the underlying mechanism and hidden variables λ of the model, but can observe only the average probability P(a b|x y) (for example, by rotating polarizers along different directions x,y and counting detector clicks a,b). It is this later sort of superluminal communication that we show to be an intrinsic feature of any v-causal model reproducing quantum correlations.
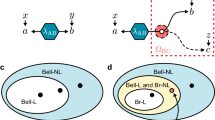
A sufficient condition for correlations P not to be exploitable for superluminal communication is that they satisfy a series of mathematical constraints known as the no-signalling conditions. In the case of four parties (on which we will focus below), no-signalling is the condition that the marginal distributions for the joint system ABC are independent of the measurement performed on system D, that is,

together with the analogous conditions for systems ABD, ACD and BCD. Here P(a b c d|x y z w) is the probability that the four parties observe outcomes a,b,c and d when their respective measurements settings are x,y,z and w. These conditions imply that the marginal distribution for any subset of systems is independent of the measurements performed on the complementary subset.
Our main result is based on the following Lemma, whose proof can be found in Supplementary Information SB.
Lemma. Let P(a b c d|x y z w) be a joint probability distribution with a,b,c,d∈{0,1} and x,y,z,w∈{0,1} satisfying the following two conditions: first, the conditional bipartite correlations BC|AD are local, that is, the joint probabilities P(b c|y z,a x d w) for systems BC conditioned on the measurement settings and results of systems AD admit a decomposition of the form  for every a,x,d,w; and second, P satisfies the no-signalling conditions (1). Then there exists a four-partite Bell expression S (see Supplementary Information SB for its description) such that correlations satisfying these two both conditions necessarily satisfy S≤7. On the other hand, there exist local measurements on a four-partite entangled quantum state that yield S≃7.2>7.
for every a,x,d,w; and second, P satisfies the no-signalling conditions (1). Then there exists a four-partite Bell expression S (see Supplementary Information SB for its description) such that correlations satisfying these two both conditions necessarily satisfy S≤7. On the other hand, there exist local measurements on a four-partite entangled quantum state that yield S≃7.2>7.
The Bell expression S has the extra property that it involves only the marginal correlations ABD and ACD, but does not contain correlation terms involving both B and C (this property is crucial for establishing our final result, as it implies that a violation of the Bell inequality can be verified without requiring the measurement on B and C to be simultaneous).
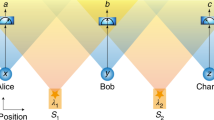
Consider now the prediction of a v-causal model in the thought experiment depicted in Fig. 3, where the spacetime ordering between the parties in the privileged frame is such that A
As B and C are both measured after A and D and satisfy B∼C, the BC|ADcorrelations produced by a v-causal model are local (see Supplementary Information SC). A violation of the inequality of Lemma by the model therefore implies that the corresponding correlations must violate the no-signalling conditions (1). At least one of the tripartite correlations ABC, ABD, ACD or BCD must then depend on the measurement setting of the remaining party. The marginal ABD (ACD) cannot depend on z (y), because this measurement setting is freely chosen at C (B), which is outside the past v-cone of A, B (C) and D (see also Supplementary Information SD). It thus follows that either the marginal ABC must depend on the measurement setting w of system D or that the marginal BCD must depend on the measurement setting x of system A (or both). Let the four systems lie along some spatial direction at, respectively, a distance dB = (1/4)(1+(1/r))+(1/(1+r)), dC = (3/4)(1+(1/r))−(1/(1+r)), dD = 1 from A, where r = v/c>1, and let them be measured at times tA = 0, tB = tC = 2/(c+v), tD = 1/v. Suppose that the BCD marginal correlations depend on the measurement x made on the first system A. If parties B and C broadcast (at light speed) their measurement results, it will be possible to evaluate the marginal correlations BCD, at the point D′. As this point lies outside the future light cone of A (shaded area), this scheme can be used for superluminal communication from A to D′. Similarly, if the ABC marginal correlations depend on the measurement w made on D, they can be used for superluminal communication from D to the point A′.
Explicitly, consider a modification of the thought experiment of Fig. 3, where the times tB and tC at which B and C are measured are chosen randomly so that any of the three configurations A
In stark contrast with the bipartite scenario, these results therefore allow one to test experimentally the prediction of no-signalling v-causal models for any  without requiring any simultaneous measurements. Indeed, the very same theoretical argument as that presented in the last paragraph can be used to deduce the value of S in the case B∼C by measuring the marginals ABD and ACD in situations in which B and C are not necessarily outside each other’s v-cones. For a more detailed discussion on some of the experimental possibilities that follow from our result, see Supplementary Information SE. Note that as with usual Bell experiments, depending on the assumption that one is willing to take, an experimental test of v-causal models may also need to overcome various loopholes. The way to remove these assumptions and overcome these loopholes is an interesting question that goes beyond the scope of our work but some possibilities are discussed in Supplementary Information SE.
without requiring any simultaneous measurements. Indeed, the very same theoretical argument as that presented in the last paragraph can be used to deduce the value of S in the case B∼C by measuring the marginals ABD and ACD in situations in which B and C are not necessarily outside each other’s v-cones. For a more detailed discussion on some of the experimental possibilities that follow from our result, see Supplementary Information SE. Note that as with usual Bell experiments, depending on the assumption that one is willing to take, an experimental test of v-causal models may also need to overcome various loopholes. The way to remove these assumptions and overcome these loopholes is an interesting question that goes beyond the scope of our work but some possibilities are discussed in Supplementary Information SE.
We proved that if a v-causal model satisfies the requirement of reproducing the quantum correlations when the different systems are each within the range of causal influences of previously measured systems, then such a model will necessarily lead to superluminal signalling, for any finite value of v>c. Moreover, our result opens a whole new avenue of experimental possibilities for testing v-causal models. It also illustrates the difficulty to modify quantum physics while maintaining no-signalling. If we want to keep no-signalling, it shows that quantum non-locality must necessarily relate discontinuously parts of the universe that are arbitrarily distant. This gives further weight to the idea that quantum correlations somehow arise from outside spacetime, in the sense that no story in space and time can describe how they occur.
References
Bell, J. S. Speakable and Unspeakable in Quantum Mechanics: Collected Papers on Quantum Philosophy (Cambridge Univ. Press, 2004).
Aspect, A. Bell’s inequality test: More ideal than ever. Nature 398, 189 (1999).
Salart, D., Baas, A., Branciard, C., Gisin, N. & Zbinden, H. Testing the speed of ‘spooky action at a distance’. Nature 454, 861–864 (2008).
Cocciaro, B., Faetti, S. & Fronzoni, L. A lower bound for the velocity of quantum communications in the preferred frame. Phys. Lett. A 375, 379–384 (2011).
Einstein, A., Podolsky, B. & Rosen, N. Can quantum-mechanical description of physical reality be considered complete? Phys. Rev. 47, 777–780 (1935).
Aspect, A., Dalibard, J. & Roger, G. Experimental test of Bell’s inequalities using time-varying analyzers. Phys. Rev. Lett. 49, 1804–1807 (1982).
Tittel, W., Brendel, J., Zbinden, H. & Gisin, N. Violation of Bell inequalities by photons more than 10 km apart. Phys. Rev. Lett. 81, 3563–3566 (1998).
Weihs, G., Jennewein, T., Simon, C., Weinfurter, H. & Zeilinger, A. Violation of Bell’s inequality under strict Einstein locality conditions. Phys. Rev. Lett. 81, 5039–5043 (1998).
Norsen, T. & John, S. Bell’s concept of local causality. Am. J. Phys. 79, 1261–1275 (2012).
Mauldin, T. Quantum Non-Locality and Relativity: Metaphysical Intimations of Modern Physics (Blackwell Publishers, 2002).
Shimony, A. Search for a Naturalistic World View: Scientific Method and Epistemology (Cambridge Univ. Press, 1993).
Popescu, S. & Rohrlich, D. Quantum nonlocality as an axiom. Found. Phys. 24, 379–385 (1994).
Bohm, D. & Hiley, B. J. The Undivided Universe 347 (Routledge, 1993).
Scarani, V. & Gisin, N. Superluminal influences, hidden variables, and signaling. Phys. Lett. A 295, 167–174 (2002).
Scarani, V. & Gisin, N. Superluminal hidden communication as the underlying mechanism for quantum correlations: Constraining models. Braz. J. Phys. 35, 328–332 (2005).
Coretti, S., Hänggi, E. & Wolf, S. Nonlocality is Transitive. Phys. Rev. Lett. 107, 100402 (2011).
Lineweaver, C. H. et al. The Dipole Observed in the COBE DMR 4 Year Data. Astrophys. J 470, 38–42 (1996).
Bohm, D. A suggested interpretation of the quantum theory in terms of ‘Hidden’ variables. I. Phys. Rev. 85, 166–179 (1952).
Bohm, D. A suggested interpretation of the quantum theory in terms of ‘Hidden’ variables. II. Phys. Rev. 85, 180–193 (1952).
Ghirardi, G. C., Rimini, A. & Weber, T. Unified dynamics for microscopic and macroscopic systems. Phys. Rev. D 34, 470–491 (1986).
Tumulka, R. in AIP Conf. Proc. 844 (eds Bassi, A., Duerr, D., Weber, T. & Zanghi, N.) 340–352 (American Institute of Physics, 2006).
Bell, J. S. Speakable and Unspeakable in Quantum Mechanics Ch. 24 (Cambridge Univ. Press, 2004).
Acknowledgements
We acknowledge S. Massar and T. Vértesi for helpful discussions as well as J. Silman, E. Cavalcanti, T. Barnea and S. Portmann for comments on the manuscript. This work was supported by the European ERC AG Qore and SG PERCENT, the European EU FP7 QCS and Q-Essence projects, the CHIST-ERA DIQIP project, the Swiss NCCRs QP and QSIT, the Interuniversity Attraction Poles Photonics@be Programme (Belgian Science Policy), the Brussels-Capital Region through a BB2B Grant, the Spanish FIS2010-14830 project, the National Research Foundation and the Ministry of Education of Singapore.
Author information
Authors and Affiliations
Contributions
All authors participated at various levels in the results presented here and in the writing of the article.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Information (PDF 347 kb)
Rights and permissions
About this article
Cite this article
Bancal, JD., Pironio, S., Acín, A. et al. Quantum non-locality based on finite-speed causal influences leads to superluminal signalling. Nature Phys 8, 867–870 (2012). https://doi.org/10.1038/nphys2460
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys2460
This article is cited by
-
Testing the speed of “spooky action at a distance” in a tabletop experiment
Scientific Reports (2023)
-
Two roads to retrocausality
Synthese (2022)
-
A Non-Spatial Reality
Foundations of Science (2021)
-
The relativistic causality versus no-signaling paradigm for multi-party correlations
Nature Communications (2019)
-
Emergent Quantum Mechanics and the Origin of Quantum Non-local Correlations
International Journal of Theoretical Physics (2017)