Abstract
There are two known distinct types of the integer quantum Hall effect. One is the conventional quantum Hall effect, characteristic of two-dimensional semiconductor systems1,2, and the other is its relativistic counterpart observed in graphene, where charge carriers mimic Dirac fermions characterized by Berry’s phase π, which results in shifted positions of the Hall plateaus3,4,5,6,7,8,9. Here we report a third type of the integer quantum Hall effect. Charge carriers in bilayer graphene have a parabolic energy spectrum but are chiral and show Berry’s phase 2π affecting their quantum dynamics. The Landau quantization of these fermions results in plateaus in Hall conductivity at standard integer positions, but the last (zero-level) plateau is missing. The zero-level anomaly is accompanied by metallic conductivity in the limit of low concentrations and high magnetic fields, in stark contrast to the conventional, insulating behaviour in this regime. The revealed chiral fermions have no known analogues and present an intriguing case for quantum-mechanical studies.
Similar content being viewed by others
Main
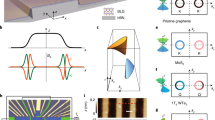
Figure 1 provides a schematic overview of the quantum Hall effect (QHE) behaviour observed in bilayer graphene by comparing it with the conventional integer QHE. In the standard theory, each filled single-degenerate Landau level contributes one conductance quantum e2/h towards the observable Hall conductivity (here e is the electron charge and h is Planck’s constant). The conventional QHE is shown in Fig. 1a, where plateaus in Hall conductivity σx y make up an uninterrupted ladder of equidistant steps. In bilayer graphene, QHE plateaus follow the same ladder but the plateau at zero σx y is markedly absent (Fig. 1b). Instead, the Hall conductivity undergoes a double-sized step across this region. In addition, longitudinal conductivity σx x in bilayer graphene remains of the order of e2/h, even at zero σx y. The origin of the unconventional QHE behaviour lies in the coupling between two graphene layers, which transforms massless Dirac fermions, characteristic of single-layer graphene3,4,5,6,7,8,9 (Fig. 1c), into a new type of chiral quasiparticle. Such quasiparticles have an ordinary parabolic spectrum ɛ(p)=p2/2m with effective mass m, but accumulate Berry’s phase of 2π along cyclotron trajectories (here ɛ is the energy of quasiparticles and p their momentum). The latter is shown to be related to a peculiar quantization where the two lowest Landau levels lie exactly at zero energy ɛ, leading to the missing plateau and double step shown in Fig. 1b.
a,b, Schematic illustration of the conventional integer QHE found in 2D semiconductor systems (a), incorporated from refs 12, and the QHE in bilayer graphene described in the present paper (b). Plateaus in Hall conductivity σx y occur at values (g e2/h)N, where N is an integer, e2/h the conductance quantum and g the system degeneracy. The distance between steps along the concentration axis is defined by the density of states g B/φ0 on each Landau level, which is independent of a 2D spectrum1,2,3,4,5,6,7,8,9. Here, B is the magnetic field and φ0=h/e the flux quantum. The corresponding sequences of Landau levels as a function of carrier concentrations n are shown in blue and orange for electrons and holes, respectively. For completeness, c also shows the QHE behaviour for massless Dirac fermions in single-layer graphene.
Bilayer films studied in this work were made by the micromechanical cleavage of crystals of natural graphite, which was followed by the selection of bilayer flakes by using a combination of optical microscopy and atomic force microscopy as described in refs 1011. Multiterminal field-effect devices (see the inset in Fig. 2a) were made from the selected flakes by using standard microfabrication techniques. As a substrate, we used an oxidized heavily doped Si wafer, which allowed us to apply gate voltage Vg between graphene and the substrate. The studied devices showed an ambipolar electric field effect such that electrons and holes could be induced in concentrations n up to 1013 cm−2 (n=α Vg, where α≈7.3×1010 cm−2 V−1 for a 300 nm SiO2 layer). For further details about microfabrication of graphitic field-effect devices and their measurements, we refer to earlier work3,4,10,11.
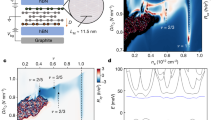
a, Hall resistivities ρx y and ρx x measured as a function of B for fixed concentrations of electrons n≈2.5×1012 cm−2 induced by the electric field effect. Inset: Scanning electron micrograph of one of more than ten bilayer devices studied in our work. The width of the Hall bar (dark central area) is approximately 1 μm. The known geometry of our devices allowed us to convert the measured resistance into ρx x with an accuracy of better than 10%. b,c, σx y and ρx x are plotted as functions of n at a fixed B and temperature T=4 K. Positive and negative n correspond to field-induced electrons and holes, respectively. The Hall conductivity σx y=ρx y/(ρx y2+ρx x2) was calculated directly from experimental curves for ρx y and ρx x. σx y allows the underlying sequences of QHE plateaus to be seen more clearly. σx y crosses zero without any sign of the zero-level plateau that would be expected for a conventional 2D system. The inset shows the calculated energy spectrum for bilayer graphene, which is parabolic at low ɛ. Carrier mobilities μ in our bilayer devices were typically around 3,000 cm2 V−1 s−1, which is lower than for devices made from single-layer graphene3,4. This is surprising because one generally expects more damage and exposure in the case of single-layer graphene that is unprotected from the immediate environment from both sides.
Figure 2a shows a typical QHE behaviour in bilayer graphene at a fixed Vg (fixed n) and varying magnetic field B up to 30 T. Pronounced plateaus are clearly seen in Hall resistivity ρx y in high B, and they are accompanied by zero longitudinal resistivity ρx x. The observed sequence of the QHE plateaus is described by ρx y=h/4N e2, which is the same sequence as expected for a two-dimensional (2D) free-fermion system with double spin and double valley degeneracy1,2,12,13,14,15. However, a clear difference between the conventional and reported QHE emerges in the regime of small filling factors ν<1 (see Figs 2b,c and 3). This regime is convenient to study by fixing B and varying concentrations of electrons and holes passing through the neutrality point |n|≈0, where ρx y changes its sign and, nominally, ν=0. Also, because carrier mobilities μ in graphitic films are weakly dependent on n, measurements in constant B are more informative3,4,10. They correspond to a nearly constant parameter μ B, which defines the quality of Landau quantization, and this allows simultaneous observation of several QHE plateaus during a single voltage sweep in moderate magnetic fields (Fig. 2b). The periodicity Δn of quantum oscillations in ρx x as a function of n is defined by the density of states g B/φ0 (where g is the degeneracy and φ0 is the flux quantum) on each Landau level1,2,3,4,5,6,7,8,9,10 (see Fig. 1). In Fig. 2c, for example, Δn≈1.2×1012 cm−2 at B=12 T, which yields g=4 and confirms the double-spin and double-valley degeneracy expected from band-structure calculations for bilayer graphene14,15.
a–d, The peak in ρx x remains of the order of h/4e2, independent of B (a,b) and T (c,d). This yields no gap in the Landau spectrum at zero energy. b, For a fixed n≈0 and varying B, we observed only small magnetoresistance. The latter varied for different devices and contact configurations (probably indicating the edge-state transport) and could be non-monotonic and of random sign. However, the observed magnetoresistance (for bilayer devices without chemical doping10) never exceeded a factor of two in any of our experiments in fields up to 20 T.
Figure 2b shows that, although the Hall plateaus in bilayer graphene follow the integer sequence σx y=±(4e2/h)N for N≥1, there is no sign of the zero-N plateau at σx y=0, which is expected for 2D free-fermion systems1,2 (Fig. 1a). In this respect, the behaviour resembles the QHE for massless Dirac fermions (Fig. 1c), where there is also no plateau but a step occurs when σx y passes the neutrality point. However, in bilayer graphene, this step has a double height and is accompanied by a central peak in ρx x, which is twice as broad as all other peaks (Fig. 2c). The broader peak yields that, in bilayer graphene, the transition between the lowest hole and electron Hall plateaus requires twice the number of carriers needed for the transition between the other QHE plateaus. This implies that the lowest Landau level has double degeneracy 2×4B/φ0, which can be viewed as two Landau levels merged together at n≈0 (see the Landau level charts in Fig. 1).
Continuous measurements through ν=0 as shown in Fig. 2b,c have been impossible for conventional 2D systems where the zero-level plateau in σx y=ρx y/(ρx y2+ρx x2) is inferred1,2 from a rapid (often exponential) increase in ρx x≫h/e2 with increasing B and decreasing temperature T for filling factors ν<1, indicating an insulating state. To provide a direct comparison with the conventional QHE measurements, Fig. 3 shows ρx x in bilayer graphene as a function of B and T around zero ν. Bilayer graphene shows little magnetoresistance or temperature dependence at the neutrality point, in striking contrast to the conventional QHE behaviour. This implies that σx y in bilayer graphene does not vanish over any interval of ν and reaches zero only at one point, where ρx y changes its sign. Note that ρx x surprisingly maintains a peak value of approximately h/g e2 in fields up to 20 T and temperatures down to 1 K. A finite value of ρx x≈h/4e2 in the limit of low carrier concentrations and at zero B was reported for single-layer graphene3. This observation was in qualitative agreement with theory, which attributes the finite metallic conductivity and the absence of localization to the relativistic-like spectrum of single-layer graphene3. Bilayer graphene has the usual parabolic spectrum, and the observation of the maximum resistivity of approximately h/4e2 and, moreover, its weak dependence on B in this system is most unexpected. Note, however, that the quantization is less accurate than in single-layer graphene, as the peak value varied from 6 to 9 kΩ for different bilayer devices.
The unconventional QHE in bilayer graphene originates from peculiar properties of its charge carriers that are chiral fermions with a finite mass, as discussed below. First, we have calculated the quasiparticle spectrum in bilayer graphene by using the standard nearest-neighbour approximation12. For quasiparticles near the corners of the Brillouin zone known as K-points, we find  , where
, where  , a is the lattice periodicity, ħ=h/2π and γ0 and γ1 are the intra layer and inter layer coupling constants, respectively13. This dispersion relation (plotted in Fig. 2c) is in agreement with the first-principle band-structure calculations14 and, at low energies, becomes parabolic ɛ=±p2/2m with m=γ1/2vF2 (the sign ± refers to electron and hole states). Further analysis15 shows that quasiparticles in bilayer graphene can be described by using the effective hamiltonian
, a is the lattice periodicity, ħ=h/2π and γ0 and γ1 are the intra layer and inter layer coupling constants, respectively13. This dispersion relation (plotted in Fig. 2c) is in agreement with the first-principle band-structure calculations14 and, at low energies, becomes parabolic ɛ=±p2/2m with m=γ1/2vF2 (the sign ± refers to electron and hole states). Further analysis15 shows that quasiparticles in bilayer graphene can be described by using the effective hamiltonian

 acts in the space of two-component Bloch functions (further referred to as pseudospins) describing the amplitude of electron waves on weakly coupled nearest sites A1 and B2 belonging to two nonequivalent carbon sublattices A and B and two graphene layers marked as 1 and 2.
acts in the space of two-component Bloch functions (further referred to as pseudospins) describing the amplitude of electron waves on weakly coupled nearest sites A1 and B2 belonging to two nonequivalent carbon sublattices A and B and two graphene layers marked as 1 and 2.
For a given direction of quasiparticle momentum p=(pcosϕ,psinϕ), a hamiltonian  of a general form
of a general form

can be rewritten as

where n=−(cosJ ϕ,sinJ ϕ) and vector  is made from Pauli matrices15. For bilayer graphene, J=2, but the notation J is useful because it also allows equation (1) to be linked with the case of single-layer graphene, where J=1. The eigenstates of
is made from Pauli matrices15. For bilayer graphene, J=2, but the notation J is useful because it also allows equation (1) to be linked with the case of single-layer graphene, where J=1. The eigenstates of  correspond to pseudospins polarized parallel (electrons) or antiparallel (holes) to the ‘quantization’ axis n. An adiabatic evolution of such pseudospin states, which accompanies the rotation of momentum p by angle ϕ, also corresponds to the rotation of axis n by angle J ϕ. As a result, if a quasiparticle encircles a closed contour in the momentum space (that is ϕ=2π), a phase shift Φ=J π known as Berry’s phase is gained by the quasiparticle’s wavefunction16. Berry’s phase can be viewed as arising owing to rotation of pseudospin, when a quasiparticle repetitively moves between different carbon sublattices (A and B for single-layer graphene, and A1 and B2 for bilayer graphene).
correspond to pseudospins polarized parallel (electrons) or antiparallel (holes) to the ‘quantization’ axis n. An adiabatic evolution of such pseudospin states, which accompanies the rotation of momentum p by angle ϕ, also corresponds to the rotation of axis n by angle J ϕ. As a result, if a quasiparticle encircles a closed contour in the momentum space (that is ϕ=2π), a phase shift Φ=J π known as Berry’s phase is gained by the quasiparticle’s wavefunction16. Berry’s phase can be viewed as arising owing to rotation of pseudospin, when a quasiparticle repetitively moves between different carbon sublattices (A and B for single-layer graphene, and A1 and B2 for bilayer graphene).
For fermions completing cyclotron orbits, Berry’s phase contributes to the semiclassical quantization and affects the phase of Shubnikov–de Haas oscillations (SdHOs). For single-layer graphene, this results in a π-shift in SdHOs and a related 1/2-shift in the sequence of QHE plateaus3,4,5,6,7,8,9, as compared with the conventional 2D systems where Berry’s phase is zero. For bilayer graphene, Φ=2π and there can be no changes in the quasiclassical limit (N≫1). One might also expect that phase 2π cannot influence the QHE sequencing. However, the exact analysis (see the Supplementary Information) of the Landau-level spectra for hamiltonian  showing Berry’s phase J π shows that there is an associated J-fold degeneracy of the zero-energy Landau level (that is Berry’s phase of 2π leads to observable consequences in the quantum limit N=0). For the free-fermion QHE systems (no Berry’s phase), the energy is given by ɛN=ħωc(N+1/2) and the lowest state lies at finite energy ħωc/2, where cyclotron frequency ωc=e B/m. For single-layer graphene (J=1, Φ=π),
showing Berry’s phase J π shows that there is an associated J-fold degeneracy of the zero-energy Landau level (that is Berry’s phase of 2π leads to observable consequences in the quantum limit N=0). For the free-fermion QHE systems (no Berry’s phase), the energy is given by ɛN=ħωc(N+1/2) and the lowest state lies at finite energy ħωc/2, where cyclotron frequency ωc=e B/m. For single-layer graphene (J=1, Φ=π),  and there is a single state ɛ0 at zero energy5,6,7,8,9. For bilayer graphene (J=2, Φ=2π),
and there is a single state ɛ0 at zero energy5,6,7,8,9. For bilayer graphene (J=2, Φ=2π),  and the two lowest states ɛ0=ɛ1 lie at zero energy15.
and the two lowest states ɛ0=ɛ1 lie at zero energy15.
The existence of a double-degenerate Landau level explains the unconventional QHE found in bilayer graphene. This Landau level lies at the border between electron and hole gases and, taking into account the quadruple spin and valley degeneracy, it accommodates carrier density 8B/φ0. With reference to Fig. 1, the existence of such a Landau level implies that there must be a QHE step across the neutrality point, similarly to the case of single-layer graphene3,4,5,6,7,8,9. Owing to the double degeneracy, it takes twice the number of carriers to fill it (as compared with all other Landau levels), so that the transition between the corresponding QHE plateaus must be twice as wide (that is 8B/φ0 as compared with 4B/φ0). Also, the step between the plateaus must be twice as high, that is 8e2/h as compared with 4e2/h for the other steps at higher carrier densities. This is exactly the behaviour observed experimentally.
In conclusion, bilayer graphene adds a new member to the small family of QHE systems, and its QHE behaviour reveals the existence of massive chiral fermions with Berry’s phase 2π, which are distinct from other known quasiparticles. The observation of a finite metallic conductivity of approximately e2/h for such fermions poses a serious challenge for theory.
References
Prange, R. E. & Girvin, S. M. The Quantum Hall Effect (Springer, New York, 1990).
Macdonald, A. H. Quantum Hall Effect: A Perspective (Kluwer Academic, Dordrecht, 1990).
Novoselov, K. S. et al. Two-dimensional gas of massless Dirac fermions in graphene. Nature 438, 197–200 (2005).
Zhang, Y., Tan, J. W., Stormer, H. L. & Kim, P. Experimental observation of the quantum Hall effect and Berry’s phase in graphene. Nature 438, 201–204 (2005).
McClure, J. W. Diamagnetism of graphite. Phys. Rev. 104, 666–671 (1956).
Haldane, F. D. M. Model for a quantum Hall effect without Landau levels: Condensed-matter realization of the ‘parity anomaly’. Phys. Rev. Lett. 61, 2015–2018 (1988).
Zheng, Y. & Ando, T. Hall conductivity of a two-dimensional graphite system. Phys. Rev. B 65, 245420 (2002).
Gusynin, V. P. & Sharapov, S. G. Unconventional integer quantum Hall effect in graphene. Phys. Rev. Lett. 95, 146801 (2005).
Peres, N. M. R., Guinea, F. & Castro Neto, A. H. Electronic properties of two-dimensional carbon. Preprint at <http://arxiv.org/abs/cond-mat/0506709> (2005).
Novoselov, K. S. et al. Electric field effect in atomically thin carbon films. Science 306, 666–669 (2004).
Novoselov, K. S. et al. Two dimensional atomic crystals. Proc. Natl Acad. Sci. USA 102, 10451–10453 (2005).
Wallace, P. R. The band theory of graphite. Phys. Rev. 71, 622–634 (1947).
Dresselhaus, M. S. & Dresselhaus, G. Intercalation compounds of graphite. Adv. Phys. 51, 1–186 (2002).
Trickey, S. B., Müller-Plathe, F., Diercksen, G. H. F. & Boettger, J. C. Interplanar binding and lattice relaxation in a graphite delayer. Phys. Rev. B 45, 4460–4468 (1992).
McCann, E. & Falko, V. I. Landau level degeneracy and quantum Hall effect in a graphite bilayer. Preprint at <http://arxiv.org/abs/cond-mat/0510237> (2005).
Berry, M. V. Quantal phase factor accompanying adiabatic change. Proc. R. Soc. Lond. A 392, 45–57 (1984).
Acknowledgements
We thank the High Field Magnet Laboratory (Nijmegen) for their hospitality. U.Z. and K.S.N. were partially supported by EuroMagNET of the 6th Framework ‘Structuring the European Research Area, Research Infrastructures Action’ and by the Leverhulme Trust. S.V.M. acknowledges support from the Russian Academy of Sciences. This research was funded by the EPSRC (UK).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
41567_2006_BFnphys245_MOESM1_ESM.pdf
Supplementary Information: J-fold degeneracy of the lowest Landau level for chiral fermions described by Hamiltonian (PDF 29 kb)
Rights and permissions
About this article
Cite this article
Novoselov, K., McCann, E., Morozov, S. et al. Unconventional quantum Hall effect and Berry’s phase of 2π in bilayer graphene. Nature Phys 2, 177–180 (2006). https://doi.org/10.1038/nphys245
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys245
This article is cited by
-
Engineering correlated insulators in bilayer graphene with a remote Coulomb superlattice
Nature Materials (2024)
-
Impurity atoms effects on electronic properties and Seebeck coefficient of armchair graphene like nanoribbon
Applied Physics A (2024)
-
Stacking transfer of wafer-scale graphene-based van der Waals superlattices
Nature Communications (2023)
-
Thermally stable quantum Hall effect in a gated ferroelectric-graphene heterostructure
Communications Physics (2023)
-
Superconductivity and correlated phases in non-twisted bilayer and trilayer graphene
Nature Reviews Physics (2023)