Abstract
Magnetic monopoles1 are point-like sources of magnetic field, never observed as fundamental particles. This has triggered the search for monopole analogues in the form of emergent particles in the solid state, with recent observations in spin-ice crystals2,3,4 and one-dimensional ferromagnetic nanowires5. Alternatively, topological excitations of spinor Bose–Einstein condensates have been predicted to demonstrate monopole textures6,7,8. Here we show the formation of monopole analogues in an exciton–polariton spinor condensate hitting a defect potential in a semiconductor microcavity. Oblique dark solitons are nucleated in the wake of the defect9,10 in the presence of an effective magnetic field acting on the polariton pseudo-spin11. The field splits the integer soliton into a pair of oblique half-solitons12 of opposite magnetic charge, subject to opposite effective magnetic forces. These mixed spin-phase excitations thus behave like one-dimensional monopoles13. Our results open the way to the generation of stable magnetic currents in photonic quantum fluids.
Similar content being viewed by others
Main
Magnetic monopoles are the magnetic counterparts of electric charges, characterized by a divergent field. The seminal work of Dirac1 showed that monopoles are not forbidden by the laws of quantum mechanics. In particular, he considered particles characterized by a wavefunction with a nodal line and a non-integrable phase around it. One route to create an object behaving like a monopole is thus to engineer a wavefunction with such characteristics. A model system to do this is a spinor Bose–Einstein condensate14,15,16, demonstrating properties such as superfluidity or persistent currents. In reduced dimensions, not only do these quantum fluids support topological defects17, such as vortices (two dimensional; 2D) or solitons (1D) characterized by a node, but an adequate spin distribution can also provide a vector field with a non-zero divergence, satisfying Maxwell’s equations for a point magnetic charge6,7,8. Monopoles can then be arranged in spinor condensates in the form of mixed spin-phase topological excitations, with a magnetic analogue of the Coulomb force acting on them13.
Exciton–polariton (polariton) condensates seem a well-suited system to evidence and study such original effects in quantum fluids. Polaritons are the quasi-particles arising from the strong coupling between excitons and photons confined in planar semiconductor microcavities (InGaAs/GaAs/AlGaAs in our case)18. Polariton fluids are easy to manipulate with standard optical techniques19,20,21,22 and they have recently become a model system for the study of quantum fluid effects such as superfluidity23, vortex formation24,25 or oblique solitons9,10. Their spin structure is especially interesting: polaritons are bosons with only two allowed spin projections ±1 on the growth axis of the sample, which couple to circularly polarized (σ±) photons in andout of the cavity. A coherent superposition of different spin populations gives rise to polarization states that can be described by a pseudospin vector S mapped onto a Bloch sphere (Fig. 1a). Another remarkable feature of microcavities is the presence of an effective in-plane magnetic field (Fig. 1b) induced by the polarization splitting between the transverse electric (TE)–transverse magnetic (TM) polarization modes11. The effective field interacts with the polariton pseudospin, adding a magnetic energy term  to the Hamiltonian (see Supplementary Information) and it provides the analogue of a Coulomb force acting on topological monopoles13. Finally, polariton–polariton interactions are strongly spin-anisotropic of the antiferromagnetic type26. This is an absolute requirement for the observation of any stable monopole structure7,8. Indeed, a topological monopole in a two-component spinor condensate is stable against its destruction by an in-plane effective magnetic field if the difference in the interaction energy between the same and opposite spins exceeds the magnetic energy13.
to the Hamiltonian (see Supplementary Information) and it provides the analogue of a Coulomb force acting on topological monopoles13. Finally, polariton–polariton interactions are strongly spin-anisotropic of the antiferromagnetic type26. This is an absolute requirement for the observation of any stable monopole structure7,8. Indeed, a topological monopole in a two-component spinor condensate is stable against its destruction by an in-plane effective magnetic field if the difference in the interaction energy between the same and opposite spins exceeds the magnetic energy13.
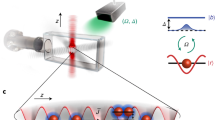
a, Bloch sphere representing all of the possible spin configurations of the polariton gas and the associated polarizations: the poles represent circular polarization, the equator represents linearly polarized states and the intermediate latitudes represent elliptically polarized states. b, Direction of the effective magnetic field created by the TE–TM splitting for polaritons propagating in different directions. c, Scheme of the resonant injection of the polariton fluid above a round potential barrier present in the sample. Half-solitons nucleate in its wake. α is the angle of incidence of the excitation beam with respect to the normal to the microcavity plane.
One kind of spin-phase topological defect already reported in polariton quantum fluids are the so-called half-vortices27,28. However, no probing of the monopole behaviour has been possible yet, because of the disorder-induced pinning28. The 1D counterpart of a half-vortex is a dark half-soliton, characterized by a notch in the polariton density of the fluid, and a simultaneous phase and polarization rotation of up to π/2 in the condensate wavefunction across the soliton12.
Here, we report on the experimental observation of oblique half-solitons and on their separation and acceleration caused by the effective magnetic field present in semiconductor microcavities. Oblique solitons (or half-solitons in the spinor case) are formed in the wake of a localized potential barrier present in the path of a flowing condensate9. They can be seen as the trajectories of 1D solitons in the direction perpendicular to the flow (x), travelling across a 2D flow. The second spatial coordinate (y, parallel to the flow) represents the time coordinate of the 1D system (t = y/vf, where vf is the flow velocity). This means that the soliton trajectory becomes traceable in a steady state regime29. Studying such trajectories, we demonstrate that an integer oblique soliton separates into a pair of half-solitons of opposite magnetic charge accelerated in opposite directions.
In our experiments we create a polariton fluid in a semiconductor microcavity (see Methods) at a temperature of 10 K by quasi-resonant excitation of the lower polariton branch with a continuous wave Ti:sapphire monomode laser. Polarization-resolved real-space images of the polariton fluid in the transmission geometry are then recorded on a CCD (charge-coupled device) camera owing to the photons escaping out of the cavity (Fig. 1c). The fluid is injected at supersonic speed (in-plane momentum of kP = 1.3 μm−1, see Methods), upstream from the potential barrier formed by a structural photonic defect present in our sample. Under these conditions, a circularly polarized excitation beam leads to the formation of pairs of oblique dark solitons in the wake of the barrier9, characterized by a phase jump close to π across each notch (see Supplementary Information). In the present experiments, we create a polariton gas with linear polarization parallel to the flow (TM polarization, along the y direction). This is a key feature needed to explore the nucleation of spin-phase topological excitations, which can be evidenced by analysing the circularly polarized components of the emission.
First, we demonstrate the formation of half-integer solitons. Figure 2a-I shows the nucleation of two oblique dark solitons to the right of the barrier wake in the σ+ component of the emission. They can be identified as dark straight notches in the polariton density. These solitons are almost absent in the σ− component (Fig. 2a-II). In turn, in the σ− emission, a deep soliton (S1) clearly appears to the left of the barrier wake (blue arrow), where only a very shallow one is present in σ+ (see the profiles in Fig. 2c). The absence of mirror symmetry between Fig. 2a-I and a-II arises from the specific and uncontrolled form of the natural potential barrier. The individual dark solitons in each of the Sz = ±1 states of the fluid appear as long spatial traces with a high degree of circular polarization (ρc = (I+−I−)/(I++I−), where I±is the emitted intensity in σ± polarization), as shown in Fig. 3a. Interferometric images obtained by combining the real-space emission with a reference beam of homogeneous phase (Fig. 2b-I and b-II) give access to the phase jump across each soliton. For instance, for the soliton S1 observed in σ−, 42 μm after the obstacle we measure a phase jump of Δθ− = 0.85π (Fig. 2e; note that it would be π for a strict dark soliton with zero density at its centre9), whereas in the same region the phase in the σ+ component does not change (Δθ+≈0).
a, Emitted intensity of the polariton gas in σ+ (I) and σ− (II) circularly polarized components and in the diagonal (III) and antidiagonal (IV) linearly polarized components with respect to the TM polarization of injection. Half-solitons spontaneously nucleate in the wake of the potential barrier (dashed circle in a-I) and are evidenced as dark traces present only in one circular polarization component (arrows). The yellow line is a guide to the eye. S1 indicates the half-soliton discussed in the text. b, Corresponding interferometric images obtained from the interference of the real-space emission with a beam of homogeneous phase. c,d, Density profiles of the σ+ and σ− (c), and diagonal and antidiagonal (d) polarized emission along the dotted line in a-I–IV. The arrows indicate the position of the inner half-solitons, present only in a given circular polarization and in both diagonal polarizations. e,f, Associated phase jump (obtained from b-I–IV). The phase jumps observed in diagonal/antidiagonal polarizations have half the value of that measured in circular polarization, hence the term half-solitons. D represents diagonal and A antidiagonal polarized emmisions in d and f. The error bars in the estimation of the phase jumps shown in e and f represent ±0.08π.
a,b, Left panels, the measured degree of circular and diagonal polarizations, respectively; right panels, the calculated patterns from the solution of the nonlinear spin-dependent Schrödinger equation describing the system in the conditions of the experiment (see Supplementary Information). The dashed lines show the trajectory of the inner (grey) and outer (black) half-solitons extracted from Fig. 2a-I and a-II. The trajectories of the half-solitons appear as extremes of circular polarization, and as domain walls in diagonal polarization. The grey arrows in b indicate the direction of acceleration of the half-solitons induced by the effective magnetic field.
A dark soliton present in just one spin component of the fluid is the fingerprint of a half-soliton12. The mixed spin-phase character of these topological excitations is further evidenced when analysing them in the linear polarization basis. In the regions where the two circular polarizations are of equal intensity (that is, the fluid surrounding the half-solitons) we can define a linear polarization angle η = (θ+−θ−)/2 and a global phase ϕ = (θ++θ−)/2, where θ+ and θ− are the local phases of each circularly polarized component12,27. In our experiments we directly access the phase jump Δϕ and the change of η across the solitons by studying the linearly polarized emission in the diagonal and anti-diagonal directions (polarization plane rotated by +45° and −45° with respect to the TM direction). Figure 2d,f shows that the half-soliton S1 is also present in these polarizations with a phase jump of Δϕ≈0.4π. This confirms that across the half-solitons, ϕ undergoes a jump Δϕ≈0.85π/2≈(Δθ++Δθ−)/2, that is, one-half the phase jump observed in the circularly polarized component in which the soliton is present. We also expect a similar jump Δη of the direction of polarization. This is demonstrated in Fig. 3b, where all the half-solitons present in our fluid (dashed lines extracted from Fig. 2a-I and a-II) appear as walls between domains of diagonal (magenta) and anti-diagonal (green) polarization. Mapping the linear polarization vector in the vicinity of soliton S1 (Fig. 4a), we deduce a jump of the polarization direction of Δη≈0.32π (Fig. 4c), close to Δϕ, the ideal expected value.
a, Complete spin texture of the polariton fluid in the region between 30 and 50 μm below the barrier. The colour scale indicates the degree of circular polarization (latitude in the Bloch sphere), and the arrows the direction of the linear polarization as defined in the equator of the Bloch sphere. b, Higher magnification of the area outlined by a white rectangle in a. The half-soliton, marked by a white dashed line in a and b, provides a pseudospin field analogous to that of a point charge in the direction perpendicular to its trajectory (white dotted line). The TE–TM effective magnetic field (ΩTE–TM) has a component Ωα perpendicular to the half-soliton, which exerts a force Fmag causing it to accelerate at amag. c, Angle of the linear polarization plane measured along the direction perpendicular to the half-soliton (shown in b as green arrows along the dotted white line). The angle jumps from the antidiagonal to the diagonal direction when crossing the half-soliton.
Analysing the half-soliton trajectory from polarization-resolved real-space measurements, we study their acceleration in the field  originating from the TE–TM splitting present in the structure11, pointing in the direction of the flow (y, red arrow in Fig. 1b). The acceleration arises from the interaction between this magnetic field and the pseudospin texture of the half-soliton, shown in Fig. 4b for S1. In the direction perpendicular to the soliton (dotted line), the in-plane pseudospin S is divergent, because it points away from S1 on both sides, as expected for a magnetic charge.
originating from the TE–TM splitting present in the structure11, pointing in the direction of the flow (y, red arrow in Fig. 1b). The acceleration arises from the interaction between this magnetic field and the pseudospin texture of the half-soliton, shown in Fig. 4b for S1. In the direction perpendicular to the soliton (dotted line), the in-plane pseudospin S is divergent, because it points away from S1 on both sides, as expected for a magnetic charge.
We are able to evaluate the force acting on the half-soliton as the gradient of the magnetic energy with respect to the half-soliton position x0. The magnetic energy per unit length is  , where the integral is performed along the x′ transverse direction, perpendicular to the half-soliton located at x0. The energy has a positive contribution from the left of the half-soliton (S and
, where the integral is performed along the x′ transverse direction, perpendicular to the half-soliton located at x0. The energy has a positive contribution from the left of the half-soliton (S and  pointing in opposite directions), and a negative one from the right (S and
pointing in opposite directions), and a negative one from the right (S and  having the same direction). For the magnetic energy to be minimized, a magnetic force appears, pushing the half-soliton towards the left, increasing the negative contribution. As solitons are density notches, their effective mass is negative17 and, therefore, the acceleration is in the direction opposite to the force. Thus, the half-soliton S1 that appears in the σ− component of the fluid accelerates towards the right, as sketched in Fig. 4b. The direction of the acceleration is opposite for the soliton present in the σ+ component (see arrows in Fig. 3b).
having the same direction). For the magnetic energy to be minimized, a magnetic force appears, pushing the half-soliton towards the left, increasing the negative contribution. As solitons are density notches, their effective mass is negative17 and, therefore, the acceleration is in the direction opposite to the force. Thus, the half-soliton S1 that appears in the σ− component of the fluid accelerates towards the right, as sketched in Fig. 4b. The direction of the acceleration is opposite for the soliton present in the σ+ component (see arrows in Fig. 3b).
The monopole dynamics allows an understanding of the mechanisms of formation of the half-solitons in our experiments. An integer soliton nucleated right behind the obstacle can be seen as a superposition of two half-solitons of opposite magnetic charges. The presence of the TE–TM effective magnetic field makes them experience opposite magnetic forces, leading to their separation and to the curved trajectories depicted as dashed lines in Fig. 3, a behaviour similar to the monopole separation in spin ice under a magnetic field3. The half-solitons pushed towards the centre are slowed down, gaining stability and becoming darker as the trajectory becomes parallel to the field. Those pushed outwards gain velocity and become shallower until they eventually disappear (see Supplementary Information and the black dashed lines in Fig. 3). The trajectories of these expelled secondary half-solitons are perturbed far from the obstacle axis by the presence of further solitons nucleated by the large barrier, particularly on the right side of the images. The monopole behaviour and soliton separation are well reproduced by a nonlinear Schrödinger equation including spin and the effective magnetic field present in our microcavities (see Fig. 3 and Supplementary Information). The analogy of half-solitons with magnetic monopoles goes well beyond the behaviour reported here under an applied magnetic field. Our theoretical model predicts repulsive and attractive interactions between half-solitons depending on their respective charges (see Supplementary Information).
A remarkable feature of half-soliton monopoles is that they can be thought of as charged partly photonic quasiparticles, propagating with a high velocity in a fluid that supports superflow23. Their generation can be well controlled by the phase and density engineering of the polariton wavefunction, their trajectories can be easily followed using standard optical techniques and their dynamics can be controlled by applying strain or external electric fields, which modify the effective magnetic field30. Furthermore, owing to the developed engineering of the polariton landscape19,20, we open the way to the realization of magnetronic circuits in a polariton chip.
Methods
Sample description.
The experimental observations have been performed at 10 K in a 2λ GaAs microcavity containing three In0.05Ga0.95 As quantum wells. The top and bottom Bragg mirrors embedding the cavity have, respectively, 21 and 24 pairs of GaAs/AlGaAs alternating layers with an optical thickness of λ/4, with λ being the wavelength of the confined cavity mode. The resulting Rabi splitting is 5.1 meV, and the polariton lifetime is about 10 ps. During the molecular beam epitaxy growth of the distributed Bragg reflectors, the slight mismatch between the lattice constants of each layer results in an accumulated stress that relaxes in the form of structural defects. These photonic defects create high potential barriers in the polariton energy landscape.
Excitation scheme.
To create a polariton fluid we excite the microcavity with a continuous-wave single-mode Ti:sapphire laser resonant with the lower polariton branch. We use a confocal excitation scheme in which the laser is focused in an intermediate plane where a mask is placed to hide the upper part of the Gaussian spot. Then, an image of this intermediate plane is created on the sample, producing a spot with the shape of a half-Gaussian. Polaritons are resonantly injected into the microcavity with a well-defined wave vector, in the region above the defect. In these conditions, polaritons move out of the excitation spot with a free phase, no longer imposed by the pump beam. This is essential for the observation of quantum hydrodynamic effects involving topological excitations with phase discontinuities9.
The momentum of the injected polaritons is set by the angle of incidence α of the excitation laser on the microcavity. This allows us to control the in-plane wave vector of the polariton fluid through the relation k = k0 sin(α), where k0 is the wave vector of the laser field. At the injected polariton momentum k = 1.3 μm−1, the polariton velocity is vf = ℏk/mpol = 1.5 μm ps−1 (mpol = 10−4melectron). This velocity is higher than the speed of sound of the fluid for the polariton densities of our experiments, as evidenced by the presence of ship waves upstream of the obstacle in Fig. 2a (see ref. 23). For this value of the momentum, we measure a TE–TM splitting of 20 μeV, resulting in the effective magnetic field sketched in Fig. 1b.
Polaritons are photocreated in our microcavity with TM linear polarization. This corresponds to a pseudospin pointing in the direction of the flow as marked by the arrow in Fig. 1a.
Detection scheme.
The observations reported in this work require the complete knowledge of the polariton spin. To gain this, a complete polarization tomography of the emission is performed through the measurement of the three Stokes parameters S1 = (ITE−ITM)/Itot, S2 = (ID−IA)/Itot and S3 = (Iσ+−Iσ−)/Itot, where Ij is the light intensity emitted with polarization j, and Itot is the total emitted intensity. This requires measuring six different polarizations: IH, IV, I+45, I−45, Iσ+ and Iσ−, which, respectively, represent linear horizontal, linear vertical, linear diagonal, linear anti-diagonal, left circularly and right circularly polarized emitted intensity. A combination of wave plates and polarizing beam splitters is used to image each of the polarization components of the emitted light on a CCD camera.
References
Dirac, P. A. M. Quantised singularities in the electromagnetic field. Proc. R. Soc. Lond. A 133, 60–72 (1931).
Morris, D. J. P. et al. Strings and magnetic monopoles in the spin ice Dy2Ti2O7 . Science 326, 411–414 (2009).
Bramwell, S. T. et al. Measurement of the charge and current of magnetic monopoles in spin ice. Nature 461, 956–959 (2009).
Fennell, T. et al. Magnetic Coulomb phase in the spin ice Ho2Ti2O7 . Science 326, 415–417 (2009).
Ono, T. et al. Propagation of a magnetic domain wall in a submicrometer magnetic wire. Science 284, 468–470 (1999).
Busch, T. & Anglin, J. R. Wave-function monopoles in Bose–Einstein condensates. Phys. Rev. A 60, R2669–R2672 (1999).
Stoof, H. T. C., Vliegen, E. & Al Khawaja, U. Monopoles in an antiferromagnetic Bose–Einstein condensate. Phys. Rev. Lett. 87, 120407 (2001).
Pietilä, V. & Möttönen, M. Creation of Dirac monopoles in spinor Bose–Einstein condensates. Phys. Rev. Lett. 103, 030401 (2009).
Amo, A. et al. Polariton superfluids reveal quantum hydrodynamic solitons. Science 332, 1167–1170 (2011).
Grosso, G., Nardin, G., Morier-Genoud, F., Léger, Y. & Deveaud-Plédran, B. Soliton instabilities and vortex street formation in a polariton quantum fluid. Phys. Rev. Lett. 107, 245301 (2011).
Kavokin, A., Malpuech, G. & Glazov, M. Optical spin Hall effect. Phys. Rev. Lett. 95, 136601 (2005).
Flayac, H., Solnyshkov, D. D. & Malpuech, G. Oblique half-solitons and their generation in exciton–polariton condensates. Phys. Rev. B 83, 193305 (2011).
Solnyshkov, D. D., Flayac, H. & Malpuech, G. Stable magnetic monopoles in spinor polariton condensates. Phys. Rev. B 85, 073105 (2012).
Stenger, J. et al. Spin domains in ground-state Bose–Einstein condensates. Nature 396, 345–348 (1998).
Leanhardt, A. E., Shin, Y., Kielpinski, D., Pritchard, D. E. & Ketterle, W. Coreless vortex formation in a spinor Bose–Einstein condensate. Phys. Rev. Lett. 90, 140403 (2003).
Sadler, L. E., Higbie, J. M., Leslie, S. R., Vengalattore, M. & Stamper-Kurn, D. M. Spontaneous symmetry breaking in a quenched ferromagnetic spinor Bose–Einstein condensate. Nature 443, 312–315 (2006).
Pitaevskii, L. & Strindgari, S. Bose–Einstein Condensation (Clarendon, 2003).
Kavokin, A., Baumberg, J. J., Malpuech, G. & Laussy, F. P. Microcavities (Oxford Univ. Press, 2007).
Amo, A. et al. Light engineering of the polariton landscape in semiconductor microcavities. Phys. Rev. B 82, 081301 (2010).
Wertz, E. et al. Spontaneous formation and optical manipulation of extended polariton condensates. Nature Phys. 6, 860–864 (2010).
Sanvitto, D. et al. All-optical control of the quantum flow of a polariton superfluid. Nature Photon. 5, 610–614 (2011).
Tosi, G. et al. Sculpting oscillators with light within a nonlinear quantum fluid. Nature Phys. 8, 190–194 (2012).
Amo, A. et al. Superfluidity of polaritons in semiconductor microcavities. Nature Phys. 5, 805–810 (2009).
Lagoudakis, K. G. et al. Quantized vortices in an exciton–polariton condensate. Nature Phys. 4, 706–710 (2008).
Nardin, G. et al. Hydrodynamic nucleation of quantized vortex pairs in a polariton quantum fluid. Nature Phys. 7, 635–641 (2011).
Renucci, P. et al. Microcavity polariton spin quantum beats without a magnetic field: A manifestation of Coulomb exchange in dense and polarized polariton systems. Phys. Rev. B 72, 075317 (2005).
Rubo, Y. G. Half vortices in exciton polariton condensates. Phys. Rev. Lett. 99, 106401–106404 (2007).
Lagoudakis, K. G. et al. Observation of half-quantum vortices in an exciton–polariton condensate. Science 326, 974–976 (2009).
El, G. A., Gammal, A. & Kamchatnov, A. M. Oblique dark solitons in supersonic flow of a Bose–Einstein condensate. Phys. Rev. Lett. 97, 180405 (2006).
Malpuech, G., Glazov, M. M., Shelykh, I. A., Bigenwald, P. & Kavokin, K. V. Electronic control of the polarization of light emitted by polariton lasers. Appl. Phys. Lett. 88, 111118 (2006).
Acknowledgements
We thank R. Houdré for the microcavity sample and P. Voisin for fruitful discussions. This work was supported by the Agence Nationale de la Recherche (contract ANR-11-BS10-001), the RTRA (contract Boseflow1D), IFRAF, the FP7 ITNs Clermont4 (235114) and Spin-Optronics (237252), and the FP7 IRSES ‘Polaphen’ (246912). A.B. is a member of the Institut Universitaire de France.
Author information
Authors and Affiliations
Contributions
All authors contributed to all aspects of this work.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Information (PDF 2064 kb)
Supplementary Movie
Supplementary Movie 1 (AVI 3015 kb)
Supplementary Movie
Supplementary Movie 2 (AVI 11425 kb)
Rights and permissions
About this article
Cite this article
Hivet, R., Flayac, H., Solnyshkov, D. et al. Half-solitons in a polariton quantum fluid behave like magnetic monopoles. Nature Phys 8, 724–728 (2012). https://doi.org/10.1038/nphys2406
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys2406
This article is cited by
-
Magneto-optical induced supermode switching in quantum fluids of light
Communications Physics (2023)
-
Observation of Zitterbewegung in photonic microcavities
Light: Science & Applications (2023)
-
Moiré pattern of interference dislocations in condensate of indirect excitons
Nature Communications (2021)
-
Dispersion relation of the collective excitations in a resonantly driven polariton fluid
Nature Communications (2019)
-
Edge-emitting polariton laser and amplifier based on a ZnO waveguide
Light: Science & Applications (2018)