Main

Classical and quantum dimensions are fundamental quantities in information processing. In particular, the security of many cryptographic schemes1,2,3 crucially relies on the dimensional characteristics of the information carriers. From a fundamental perspective, the difference between classical and quantum dimensions can be used for quantification of the non-classicality of correlations: classical simulation of correlations produced by a quantum system of (quantum) dimension dq may require a classical system of (classical) dimension dc≫dq (refs 4, 5, 6).

The problem of efficiently testing the minimum possible dimension spanned by a set of states has been approached from different theoretical perspectives. The concept of a quantum dimension witness was first introduced for the dimension of the Hilbert space of composite systems tested locally7, and then related to the construction of quantum random access codes8 and approached from a dynamical viewpoint9.

A device-independent approach, that is, without any reference to the internal working of the device generating the states (state preparator) was introduced recently10. In this scenario, the measurement device must be trusted. Such trust can be based on, for example, the device successfully passing suitable tests before the test of the state preparator. Moreover, one has to assume that the manufacturers of the state preparator and the measurement device do not conspire against the user. This implies that there are no secret communication channels or preprogrammed correlations between the state preparator and the measurement device.

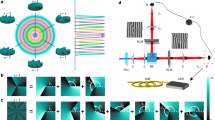
The state preparation and the tests performed under these premises are shown schematically in Fig. 1. There is a state preparator with N buttons; it emits a particle in a state ρx (specified by the device’s supplier) when button x∈{1,…,N} is pressed. For testing, the emitted particles are sent to a measurement device, with m buttons. When button y∈{1,…,m} is pressed, the device performs measurement My on the incoming particle. The measurement produces outcome b∈{−1,+1}. A complete test consists of many measurements on all of the states. It should yield a probability distribution P(b|x,y) for obtaining result b in measurement y on state ρx. Suitable combinations of the experimental probabilities P(b|x,y) can then be compared with the theoretical bounds for the values of the corresponding (classical or quantum) dimension witnesses.

Figure 1: Device-independent scenario for testing the minimum classical or quantum dimension.
figure 1

A state preparator with N buttons emits a particle in a state ρx when button x∈{1,…,N} is pressed. This particle is sent to a measurement device with m buttons. When button y∈{1,…,m} is pressed, the device performs measurement My on the particle. The measurement produces outcome b∈{−1,+1}.

Full size image

For our estimations of the lower bounds for dc and dq we use recently proposed dimension witnesses10. These witnesses use as primary quantities the expectation values

In our tests we use two combinations of these expectation values called I3 and I4. The first combination, I3, works both as a tight two-dimensional classical witness and a two-dimensional quantum witness. In other words, it allows one to identify sets of states with dc≥2 and dq≥2. It uses three preparations, which means three potentially different states (N=3) and two dichotomic measurements (m=2). The corresponding inequalities are:

where ≤bit3 means that no classical system of dimension dc=2can give a value larger than 3, and ≤qubit means that no quantum system of dimension dq=2can give a value larger than . Finally, ≤trit,qutrit 5 means that no classical system of dimension dc=3or quantum system of dimension dq=3 can give a value larger than 5, which is the algebraic maximum of I3.

The second combination, I4, tests sets of four states (N=4) and uses three dichotomic measurements (m=3). It represents witnesses represented by the following inequalities:

Thus, I4 is a dimension witness capable of identifying dc≥2,3 and dq≥2,3. One may notice that the power of the measurement devices relies to a large extent on the user’s degree of control of this device. For instance, with a limited knowledge of what the device is actually measuring, the user obtaining an outcome 5.8 for I4 will not know whether the states represent a ‘dirty’ 3-dim or 4-dim set or a quantum 2-dim set of states. On the other hand, a user who knows that the measurements were confined to a 2-dim Hilbert space can be sure that the tested set of states is genuinely quantum.

The state preparator in Fig. 2 emits photons in which information is encoded in horizontal (H) and vertical (V) polarizations, and in two spatial modes (a and b). We define four basis states: |0〉≡|H,a〉, |1〉≡|V,a〉, |2〉≡|H,b〉 and |3〉≡|V,b〉. With these encodings, any qubit state can be represented as α|H,a〉+β|V,a〉, any qutrit state as α|H,a〉+β|V,a〉+γ|H,b〉 and any ququart state as α|H,a〉+β|V,a〉+γ|H,b〉+δ|V,b〉.

Figure 2: Experimental set-up for testing classical and quantum dimension witnesses.
figure 2

The state preparator is a single-photon source emitting horizontally polarized photons that, after passing through three half-wave plates suitably oriented at angles θi (with i=1,2,3), are prepared in the required states. Information is encoded in horizontal and vertical polarizations, and in two spatial modes. The probabilities needed for the dimension witnesses are obtained from the number of detections in the detectors Di, after properly adjusting the orientations φi (with i=1,2,3) of the half-wave plates in the measurement device. QWP, quarter-wave plate; PBS, polarizing beam splitter.

Full size image

In our experiments, the photonic states were prepared as follows: a single-photon source (see the state preparator frame in Fig. 2) emitted a horizontally polarized photon. On passing through three suitably oriented half-wave plates HWP(θ1), HWP(θ2) and HWP(θ3), the state of the emitted photon was converted to the required state |ψ〉

Thus, by adjusting the HWP orientation angles θi, we could produce any of the states in the experiment. Classical sets (bits, trits, quarts) consisted of states designed to be perfectly distinguishable or identical.

The measurement device could be set in different ways. For experiments with qubit states, P(+1|x,y) was obtained from the number of detections in D1, and P(−1|x,y) was obtained from the number of detections in D3. Otherwise for experiments with qutrit states, P(+1|x,y) was obtained from the number of detections in D1 and D2, and P(−1|x,y) was obtained from the number of detections in D3. When the state preparator announced classical sets, the measurement settings became particularly simple and reduced to arranging the detectors so that they clicked on receiving a photon in a particular basis state: |0〉→D1, |1〉→D3, |2〉→D2 and |3〉→D4. The sought for measurement settings were obtained by adjusting the orientations φi of the half-wave plates HWP(φ1) and HWP(φ2) (see the measurement device frame in Fig. 2).

Our single-photon source was weak coherent light from a stabilized narrow-bandwidth diode laser emitting at 780 nm and offering a long coherence length. The laser was attenuated so that the two-photon coincidences were negligible. Our single-photon detectors (Di, i=1,2,3,4) were silicon avalanche photodiodes with detection efficiency ηd and dark counts rate Rd. For our detectors these values were around ηd≃0.55 and Rd≃400 Hz, but they varied slightly from detector to detector. The overall detection efficiency η of each Di is a product ηdηc, where ηc is the fibre coupling efficiency (with typical maximal value ηc≃0.90). To secure the same overall detection efficiency η for all of the detectors in the experiment, we measured ηd independently of the fibre coupling for each detector separately and then adjusted the coupling efficiency ηc. This calibration of the overall detection efficiencies included even the mismatches in the transmission and reflection losses in the polarization beam splitters.

The detectors Di produced output transistor–transistor logic signals of 4.1 V (with duration of 41 ns). The dead time of the detectors was 50 ns. All single counts were registered using multi-channel coincidence logic with a time window of 1.7 ns.

The first two experiments were I3 tests. The first goal was to obtain the maximum qubit violation of the bit bound I3(bit)=3. For this purpose, we prepared N=3qubit states and performed m=2 dichotomic measurements intended to maximize the value of I3. The optimal states and measurements for all experiments are described in the Methods.

The goal of the second experiment was to obtain the maximum qutrit violation of the qubit bound I3(qubit)≈3.8284. For this, we prepared N=3qutrit states and performed m=2 dichotomic measurements. The results yielded I3 very close to the algebraic bound I3=5.

The remaining experiments were I4 tests. The goal of the third experiment was to obtain the maximum qubit violation of the bit bound I4(bit)=5. We prepared N=4qubit states and performed m=3 dichotomic measurements that maximize I4. The goal of the fourth experiment was to obtain the maximum trit violation of the qubit bound I4(qubit)=6. We prepared N=4trit states and performed m=3 dichotomic measurements that maximize I4. The goal of the fifth experiment was to obtain the maximum qutrit violation of the trit bound I4(trit)=7. We prepared N=4qutrit states and performed m=3 dichotomic measurements that maximize I4. The sixth experiment was an I4 test on quarts. The goal was to obtain the maximum quart violation of the qutrit bound I4(qutrit)=7.96887. For this, we prepared N=4quart states and performed m=3 dichotomic measurements. As in the corresponding I3 test, the results gave I4 very close to the algebraic bound I4=9.

The states that saturate the witnesses boundaries may not be the most valuable for information processing. It is therefore interesting to test the dimension for the set of states that are actually used for information processing purposes. For quantum cryptography, a valuable set of states consists of four pairwise orthogonal and pairwise unbiased qubit states, such as |ψ1〉=|0〉, , |ψ3〉=|1〉 and (ref. 11). Thus, in the seventh experiment we tested the violation of the bit bound I4(dc=2)=5 by the four cryptographic states. For this, we performed the measurements maximizing the value of I4 for these states (see Methods for details). Theoretically, this maximal value is , that is, a value that clearly exceeds the bit bound I4(dc=2)=5.

All of our experimental results are summarized in Fig. 3. The obtained experimental values are in a very good agreement with the theoretical predictions. This clearly demonstrates that we are able to determine the minimum dimension of a supplied set of states. The main sources of systematic errors were due to imperfection of the optical interferometer involved in the measurements, the non-perfect overlapping of the light modes and the polarization components. The errors were deduced from propagated Poissonian counting statistics of the raw detection events, the limited precision of the settings of the polarization components (HWP plates) and the imperfection of the polarizing beam splitters. The number of detected single photons was about 1.5×105 s−1 and the coincidence to single ratio was less than 2×10−4. The measurement time for each experiment was 30 s. All of the results and their corresponding errors are listed in Table 1.

Figure 3: Experimental results of the dimension witness tests.
figure 3

The vertical dashed line labelled ‘bit’ represents the maximum value achievable with bits, and similarly for the other vertical dashed lines. I3 optimal qutrits means that the black box emits qutrit states that give the maximum value for I3 using qutrits, and similarly for the other preparations. BB84 qubits denotes the states used in standard quantum cryptography.

Full size image
Table 1 Experimental results of the dimension witness tests.
Full size table

We have experimentally determined lower bounds for the dimension of several ensembles of physical systems in a device-independent way. For the tests, we used classical and quantum dimension witnesses recently derived10. The witnesses used optimal measurements and were applied to sets of photonic bits, qubits, trits, qutrits and quarts in optimal states for maximal violation of the corresponding dimension witnesses. In addition, we applied a dimension witness I4 to the four qubit states used in standard quantum cryptography.

Our results demonstrate how dimension witnesses can be used to test classical and quantum dimensions of sets of physical states generated in externally supplied, potentially defective devices and how one can distinguish between classical and quantum sets of states of a given dimension. A very good agreement between the experimental results and the theoretical predictions makes us believe that the method can be extended to more complex witnesses and to tests of systems claiming to span higher dimensions.

Methods

Maximum qubit violation of the bit bound of I3.

To design N=3 qubit states and m=2 dichotomic measurements that maximize the value of I3, we consider the two dichotomic measurements

where denotes the identity matrix and

The three prepared states can be chosen as pure states ρx=|ψx〉〈ψx|, where

The optimization of the set-up can thus be reduced to finding the maximum of the sum of the larger eigenvalues of M1+M2 and M1−M2. This fixes parameter α to αopt=π/4 with the following result:

States |ψ1〉 and |ψ2〉 are then the corresponding eigenvectors, |ψ1〉=|1〉 and .

Maximum qutrit violation of the qubit bound of I3.

To reach the algebraic bound I3=5 with qutrits, we used

and the states |ψ1〉=|0〉, |ψ2〉=|2〉 and |ψ3〉=|1〉.

Maximum qubit violation of the bit bound of I4.

To determine the maximum qubit violation of I4, we generalize the procedure used for I3. We consider three measurements My (y=1,2,3), with |m1〉 and |m2〉 defined in (1) and (2). State |m3〉 is arbitrary. The optimization of the set-up is now reduced to maximizing the sum of the largest eigenvalues of M1−M2, M1+M2+M3 and M1+M2−M3. It brings the optimal value of α to αopt=π/6 and . The corresponding states are then the eigenvectors belonging to the maximal eigenvalues of M1+M2+M3, M1+M2−M3, M1−M2 and −M1, that is,

Maximum trit violation of the qubit bound of I4.

The optimal preparations are |ψ1〉=|ψ2〉=|0〉, |ψ3〉=|2〉 and |ψ4〉=|1〉, and the optimal measurements are

Maximum qutrit violation of the trit bound of I4.

The optimal measurements correspond to the observables of the form (1) with

The optimization proceeds as for qubits, but the algebra is more involved. We obtain

and the (unnormalized) |ψ2〉 and |ψ1〉

The optimal value of cos α is now . It gives .

Maximum quart violation of the qutrit bound of I4.

The optimal preparations are |ψ1〉=|0〉, |ψ2〉=|2〉, |ψ3〉=|1〉 and |ψ4〉=|3〉, and the optimal measurements are

Violation of the bit bound of I4 with cryptographic states.

The measurement settings maximizing the value of I4 for the standard cryptographic states are specified by the vectors

where c=cos(π/8), s=sin(π/8) and . These measurement settings give .