Abstract
Spin qubits have been successfully realized in electrostatically defined, lateral few-electron quantum-dot circuits1,2,3,4. Qubit readout typically involves spin to charge information conversion, followed by a charge measurement made using a nearby biased quantum point contact1,5,6 (QPC). It is critical to understand the back-action disturbances resulting from such a measurement approach7,8. Previous studies have indicated that QPC detectors emit phonons which are then absorbed by nearby qubits9,10,11,12,13. We report here the observation of a pronounced back-action effect in multiple dot circuits, where the absorption of detector-generated phonons is strongly modified by a quantum interference effect, and show that the phenomenon is well described by a theory incorporating both the QPC and coherent phonon absorption. Our combined experimental and theoretical results suggest strategies to suppress back-action during the qubit readout procedure.
Similar content being viewed by others
Main
The back-action process considered in this paper involves deleterious inelastic tunnelling events between two adjacent dots in a serial double or triple quantum dot (DQD, TQD). The energy difference Δ between the initial and final electronic dot states is provided by the absorption of a non-equilibrium acoustic phonon, which itself is generated by the quantum point contact (QPC) detector12. Such an absorption process between adjacent dots is constrained by the energy conservation condition Δ=ℏ|q|vph (vph is the sound velocity, q the phonon wave vector). More subtly, it is also sensitive to the difference in phase, Δ φ=d · q, of the associated phonon wave between the two dot positions, with d being the vector connecting the two dot centres14,15. This q-dependent (and hence Δ-dependent) phase difference controls the matrix element for phonon absorption because it determines whether the electron–phonon couplings in each of the two individual dots add constructively or destructively (Fig. 1 and ref. 16). The result is an oscillatory probability for inelastic electron-transfer events involving phonon absorption, with constructive interference occurring when Δ φ=(2n+1)π (where n is an integer).
a, The back-action charge fluctuations of a QPC (right) used to measure quantum dots generates locally non-equilibrium phonons (yellow and red lines); phonons emitted in the correct direction (red) can travel from the QPC to the dots and excite them from their ground state. In a semiclassical picture, the displacement wave associated with an excited phonon mode will have a maximal effect when it is exactly out of phase at the two dot sites (as shown in green), as it will cause an oscillation in the effective energy detuning between the dots. The relative phase of the wave between the dots is Δ φ=q · d, where q is the phonon wave vector, and d is the vector connecting the two dot centres; constructive interference occurs when Δ φ=(2n+1)π, with n an integer. In contrast, a minimal effect is expected when the displacement wave is in phase at the two dot sites (as shown in black). b, In a fully quantum description, absorption of a single phonon of wave vector q can occur via either the right or left dot; the amplitudes for each process add coherently to determine the final excitation probability. As ground and excited states can have different electronic probability distributions (indicated in grey), excitation leads to a measurable change in the current through the QPC charge detector. The right barrier is very opaque (thick vertical line) to suppress tunnelling between the right dot and the right lead. The blue arrow indicates the excitation and the grey arrow indicates the charge transfer between dots. c, Schematic showing the two interfering processes for absorption of back-action-generated phonons (red lines) by a DQD. The relative phase between the amplitude of each process is π+Δ φ (see equation (1)). Note that, in a given transition, the magnitude of qis determined by the energy splitting Δ between ground and excited states, whereas the direction of q is largely determined by the placement of the QPC with respect to the DQD axis. Note that an analogous interference effect involving photon absorption is not possible in our system, as the wavelength of a resonant photon would far exceed the size of the nanostructure.
Data showing a pronounced back-action effect are shown in Fig. 2a, which shows the stability diagram measured in charge detection for a few-electron DQD without a voltage drop between its left and right leads. The charge configuration of the quantum-dot structures influences the conductance of a nearby QPC because of the capacitive coupling between the dots and the QPC. To serve as a charge detector it is necessary to drive a current through the detector QPC, which, in turn, leads to the observed detector back-action. Multiple gates fabricated 85 nm above a high-mobility two-dimensional electron system (2DES) are used to define two dots and two QPCs (Fig. 2d). The differential transconductance dIQPC/dVL of the biased charge detector QPC (V QPC=−1.2 mV) is plotted as a function of control gates V L,V R. It shows local extrema at the boundaries between regions of different electronic ground states, yielding dark ‘charging’ and white ‘charge transfer’ lines. Specific ground state configurations are labelled (NL,NR), where the integer Nξ denotes the number of electrons in dot ξ=L (left) and R (right). As our DQD is cooled to T≃30 mK the unmeasured DQD is expected to be in its ground state.
a, Charge stability diagram of a DQD at V QPC=−1,200 μV, showing the differential transconductance dIQPC/dV L (in arbitrary units) numerically derived from the d.c.-current IQPC as a function of the voltages applied to gates ‘L’ and ‘R’. The number of electrons occupying the left and right dots is shown as (NL,NR) for ground state configurations. At the charging lines (dark; local transconductance minima) the overall charge NL+NR changes by one electron and at the charge transfer lines (white, local maxima) one electron moves between the dots. A triangle of back-action contains regular stripes which correspond to oscillations between the metastable configuration (1,1)and the ground-state configuration (1,2). b, Trace along the red line in a. c, Sketch of a possible back-action-induced excitation process (1,2)→(2,1)→(1,1) for (1,2) being the ground state configuration and the right tunnel barrier being closed (thick black vertical beam). d, Scanning electron micrograph of the sample structure, the approximate positions of the dots are marked in blue. The crystalline direction [110] is marked by an arrow. e, Three charge stability diagrams for V QPC=−700 μV, V QPC=−900 μV, and V QPC=−1,400 μV. The blue lines enclose the total striped area, which increases proportionally to V QPC. The dashed lines in a, b, and e correspond to Δ=|e V QPC|. f, Detuning Δmax corresponding to the size of the striped triangle as a function of V QPC for two different series of measurements for differently tuned DQD systems (data in e belong to the blue circles). The error bars contain both the uncertainty of determining the voltage-to-energy conversion (Methods) as well as the error in triangle size from the measured data. The straight line denotes Δmax=|e V QPC|.
Detector back-action manifests itself within a distinct triangular-shaped region of deviations from the ground state configuration (1, 2), where a pronounced pattern of repeated, parallel stripes is present. It indicates an oscillating probability to find the DQD in the excited configuration (1, 1). The excitation process sketched in Fig. 2c includes an inelastic tunnelling transition (1,2)→(2,1) mediated by the absorption of a phonon, followed by an elastic (and therefore quick) tunnelling process (2,1)→(1,1). In our measurements, the tunnel barrier between the right dot and right lead is tuned to be almost closed (Fig. 2c,d). The direct transition (1,1)→(1,2) back into the ground state via an elastic tunnelling process from the right lead is consequently very slow and the excited configuration (1, 1) is metastable. The associated three-level dynamics can result in average non-thermal occupations13. In this way a metastable excited state is essential to directly observe detector back-action in a low-bandwidth stability diagram measurement. It requires asymmetric dot–lead tunnel couplings in the case of a DQD (Supplementary Information).
The stripe pattern constitutes the key signature of the coherent phonon-mediated back-action effect. It indicates that the probability to be in the excited configuration (1,1) oscillates as a function of the energy detuning Δ between the intermediate state (2,1) and the ground-state configuration (1,2) (Fig. 2b); each stripe is thus parallel to the white charge transfer line where these states are degenerate (that is, Δ=0; marked). The striped region is bounded by a line Δ=Δmax, indicating that there is a maximum energy available to excite the DQD. By seeing how this boundary changes with increasing V QPC (Fig. 2e,f), we find that Δmax≃|e V QPC|, consistent with the QPC indeed being the energy source for the initial DQD excitation.
The geometry of the back-action regions as well as the influences of temperature and the orbital excitation spectrum are discussed in the Supplementary Information. In short, the remaining boundaries of the triangular-shaped regions of back-action correspond to energy thresholds for lead tunnelling. The width of each stripe is largely independent of temperature; this is indicative of an excitation process involving electron transfers between dots, without any involvement of lead electrons (Figs 2c and 3e,f). The regular spacing of the stripe features in both DQD and TQD (discussed below) experiments over so many stripes eliminates the possibility that they are due to resonances with orbital excitations of a dot, as there is no reason to expect such a uniform level spacing; furthermore, the energy spacing between the stripes is much smaller than would be expected for the average level spacing of the small dots studied here.
a–d, Charge stability diagrams of a serial TQD (differential transconductance dIQPC/dV ∼ as in Fig. 2). The linear response of IQPC is measured while the voltage applied to the gate marked with ‘∼’ is modulated by δ V ∼=1 mV r.m.s at the frequency of f=13 Hz; inset of b: scanning electron micrograph of the sample structure. Blue dots mark the approximate positions of the quantum dots. The number of electrons occupying the left, central, and right dots is shown as (NL,NC,NR) for ground state configurations. The QPC is biased by V QPC=−100, −300, −500, and −700 μV for a–d respectively. Further features are deviations from the ground state configuration caused by detector back-action. e, Sketch of a possible back-action-induced process producing the striped pattern marked by the upper arrow in the (0,1,1) region in d. A phonon is absorbed and transfers an electron from the central to the left dot. Subsequently, the electron tunnels to the left lead, lowering the overall energy (of the system including dots and leads). The resulting configuration (0,0,1) is a metastable excited state. f, Sketch of the back-action process in the (1,0,0) ground state region (lower arrow in d), which is also based on the absorption of a phonon, a short-lived intermediate, and a metastable excited state. The transitions in b and f are analogous to the process described in Fig. 2c, with the closed tunnel barrier replaced by the rightmost dot in Coulomb blockade.
To quantify the interpretation of the stripe pattern in Fig. 2 in terms of interference and QPC back-action, we have developed a theoretical model that describes the generation of phonons by the non-equilibrium QPC charge fluctuations8 and their coherent absorption by the DQD. These fluctuations represent the fundamental back-action of the measurement—their magnitude is bounded from below by the rate at which information is obtained from the QPC via a Heisenberg-like inequality8. Given this, the back-action charge noise mechanism we describe must necessarily make a contribution to the observed oscillations. This mechanism is also consistent with the high visibility of the oscillations, as such visibility requires a highly localized source of hot phonons. Although we cannot completely rule out that other, less direct, back-action mechanisms also contribute (for example, generation of hot phonons in the QPC leads), it is not clear that such mechanisms would also yield such high-visibility oscillations. We describe bulk acoustic phonon modes of GaAs interacting with both electrons in the DQD, as well as with the fluctuating charge density of the biased QPC via a screened piezoelectric interaction. Using Keldysh perturbation theory, we can calculate the DQD state in the presence of back-action (Fig. 4 and Supplementary Information). The relevant part of the dot–phonon interaction (that is, terms that can cause transitions in the dot) take the form:

Here |g〉 (|e〉) denotes the DQD ground (excited) state, tc is the pertinent interdot tunnel matrix element,  (
( ) destroys (creates) a phonon of wavector q in branch μ, λq,μ is the effective matrix element (screened) for the interaction of phonons with a single dot and h.c. denotes the Hermitian conjugate. The first bracketed factor in the sum of equation (1) denotes the key interference of relevance: the two terms correspond to phonons interacting with electrons in either the left or right dot (which are centred at rL and rR respectively) (Fig. 1b).
) destroys (creates) a phonon of wavector q in branch μ, λq,μ is the effective matrix element (screened) for the interaction of phonons with a single dot and h.c. denotes the Hermitian conjugate. The first bracketed factor in the sum of equation (1) denotes the key interference of relevance: the two terms correspond to phonons interacting with electrons in either the left or right dot (which are centred at rL and rR respectively) (Fig. 1b).
a, DQD stability diagram calculated using the theory described in the main text, which describes the emission of acoustic phonons by the non-equilibrium QPC charge fluctuations, and their coherent absorption by the double dot. Plotted is the derivative of the weighted average DQD charge 〈nR〉+ε〈nL〉 (ε≃0.4, see Methods) with respect to the gate voltage V L in the DQD experiment, as a function of the gate voltages V L and V R (see Fig. 2); this is proportional to the measured transconductance of the QPC. Parameters are taken to be the same as those in the DQD experiment; in particular, the dots and QPC are taken to be collinear and aligned with the [110] crystallographic axis. For this orientation, one finds that the so-called ‘fast transverse’ acoustic phonon mode24 makes the dominant contribution. Pronounced stripe patterns are seen, similar to the experiment. b, A cut of the calculated stability diagram in a, along the indicated red line. The suppression of oscillations at low values of ground-state-excited state energy detuning Δ is the result of screening, and is consistent with experiment. The oscillations are cut off at Δ=Δmax∼|e V qpc|, also in agreement with experiment. c, Calculated stability diagram for identical parameters as a, except that the QPC is not collinear with the two dots (the QPC–dot axis is rotated 70° from the dot–dot axis d). The result is a suppression of the back-action-induced stripe pattern. d, Calculated stability diagram for identical parameters as a, except that the orientation of the DQD–QPC axis is now rotated 20° from the [110] direction. The resulting suppression of interference is due to the anisotropy of electron–phonon interactions: the effective electron–phonon interactions are weaker in this direction. The change in orientation also causes the ‘slow transverse’ acoustic phonon mode to contribute, yielding a second, high-frequency oscillation. Insets in c and d show cuts through the stability diagram of the transconductance along the same line indicated in red in a.
Despite the explicit interference evident in equation (1), geometric averaging can still strongly suppress interference oscillations in observable quantities. Simply put, although the DQD ground-excited energy splitting fixes the magnitude of a phonon participating in an inelastic tunnelling event, it does not specify its direction; hence, the relative phase in the first term of equation (1) is not completely determined by Δ. This is typically the case in situations probing the emission of acoustic phonons by biased DQDs16, where interference oscillations are observed, albeit with much smaller visibilities than seen here17,18. In contrast, the simple geometric filtering depicted in Fig. 1a suggests that this averaging need not play a role in phonon absorption, as only phonons travelling from the QPC to the dots contribute. This is supported by our theoretical calculations, which also exhibit strong oscillations for realistic parameter values, and show a pronounced enhancement of interference oscillations when the DQD and QPC are all collinear (Fig. 4a–c).
The theory is also able to capture other aspects of the experimental data: in particular, the size of the back-action triangle grows with |V QPC|, and the lowest-energy stripes (that is, the smallest values of Δ corresponding to long phonon wavelengths) are suppressed because of screening effects (see Fig. 4b). Using the fact that in the experiment the QPC and DQD are approximately collinear, the measured spacing of the interference parameter δ Δ=45 μeV in the DQD data of Fig. 2d yields a DQD separation d=h vs/δ Δ≃250 nm; this is in good agreement with the separation estimated from scanning electron micrographs (Fig. 2d). The theory also shows that owing to the anisotropy of the electron–phonon matrix elements λq,μ, the overall magnitude of the phonon-induced back-action is sensitive to the orientation of the dot–QPC axis with respect to crystallographic axes. This dependence on orientation is demonstrated in Fig. 4d. More details on the theoretical treatment is provided in Methods and Supplementary Information.
Although we have focused so far on back-action in DQDs, the mechanism we describe is extremely general, and is in fact even more ubiquitous in systems with more than two dots. As discussed, a key requirement to see the effect is the existence of a long-lived metastable excited state. Such a situation occurs rather naturally in serial TQD structures19,20,21,22,23, as the centre dot is effectively decoupled from one of the leads whenever either one of the other two dots (left, right) is in Coulomb blockade. This directly yields a metastable excited state in which the charge of the middle dot is unable to relax. As a consequence deviations from the ground state configuration are often observed along the charging line of the centre dot20 and back-action effects occur naturally in the stability diagram. We study detector back-action in a TQD in Fig. 3 by successively increasing |e V QPC|. Already at relatively small bias |V QPC|≤300 μV (Fig. 3a,b), a triangular-shaped region of telegraph noise is observed along the central charging line20. It indicates slowly fluctuating deviations from the ground state configuration, which can be caused by external noise or detector back-action10. The underlying excitation processes, sketched in Fig. 3e,f, are similar to the one discussed above for the DQD. Indeed, the population of the right dot does not fluctuate; it plays the same role as the closed barrier in the case of the DQD, namely to block charge exchange between the centre dot and the right lead. Further increasing |V QPC| to 500 μV in (Fig. 3c) reveals the familiar pattern of equally spaced stripes, both within the (1,0,0) and (0,1,1) regions. As the bias is increased even more to |V QPC|=700 μV (Fig. 3d) the striped regions expand further, revealing the V QPC dependence also observed in the case of the DQD (Fig. 2f).
By considering experimental data on both DQD and TQD systems, we have demonstrated that interference can strongly affect the phonon-mediated back-action generated by a QPC in quantum-dot circuits. Furthermore, we have shown that this effect is well described by a basic theoretical model incorporating the generation of phonons by the QPC detector and their coherent absorption by the dots. Our study suggests the possibility of mitigating back-action effects by making use of this interference. One could, for example, endeavour to first tune the DQD/TQD to an operating point where destructive interference suppresses phonon absorption, and only then energize the QPC to make a measurement. More complex schemes that also incorporate the anisotropy of the electron–phonon interaction with respect to crystallographic axes could potentially yield even greater back-action reduction. Because the piezoelectric coupling to in-plane phonons is maximized in the 〈110〉 directions24, by aligning the QPC–DQD axis away from these directions, one could appreciably decrease the phonon-mediated back-action excitation discussed here (for example, Fig. 4a versus Fig. 4d).
Methods
Experiment.
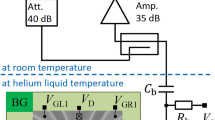
The samples were fabricated from GaAs/AlGaAs heterostructures containing 2DESs 100 nm (TQD) and 85 nm (DQD) below the surface, respectively. The 2DESs are characterized at cryogenic temperatures by carrier densities of nS=2.1×1011 cm−2 and nS=1.9×1011 cm−2 with mobilities of μ=1.72×106 cm2 Vs−1 and μ=1.19×106 cm2 Vs−1 for the TQD and DQD, respectively. Metallic gate electrodes were fabricated on the sample surface by electron-beam lithography and standard evaporation/liftoff techniques. Negative voltages applied to these electrodes are used to locally deplete the 2DESs and thereby define the quantum dot and QPC structures. All measurements were performed in dilution refrigerators at cryogenic temperatures below 100 mK. To detect the charge configuration of the TQD, the voltage of one gate of the TQD was slightly modulated and the detector differential transconductance was measured in linear response (a.c. set-up). A constant voltage was also applied across the QPC to enhance detector back-action. In the case of the DQD only a constant voltage was applied across the QPC and the direct current IQPC flowing through the QPC was measured to detect the charge configuration of the DQD (d.c. set-up). The differential transconductance dIQPC/dV L was then computed numerically. Both methods result in the differential transconductance and their interpretation is identical.
To interpret the observed back-action in terms of the energy detuning Δ between different charge configurations an accurate conversion from gate voltages to units of energy is necessary. Such a linear transformation has been performed, following the methods described elsewhere25. The conversion relation reads Δ=(αgLR−αgLL)V L+(αgRR−αgRL)V R, with the following set of conversion factors determined for the red symbols in Fig. 2f: αgLR=(54±5) meV/V , αgRR=(105±4) meV/V , αgRL=(62±4) meV/V , αgLL=(90±5) meV/V . The conversion factors related to the blue symbols in Fig. 2f read αgLR=(65±6) meV/V , αgRR=(109±7) meV/V , αgRL=(61±6) meV/V , αgLL=(97±7) meV/V .
Theory.
The fluctuating non-equilibrium QPC charge density operator  is modelled as
is modelled as  , where the total charge operator
, where the total charge operator  is described by scattering theory (see refs 8, 26). Note that as we are interested in a single-channel QPC, the spatial profile f(r) of the fluctuating QPC charge density is fixed; for simplicity, we take it to be a Gaussian of width rQPC. This fluctuating QPC charge density is coupled to acoustic phonons via the standard piezoelectric interaction (using parameters appropriate for GaAs (ref. 24)). We calculate the Keldysh Green functions of the acoustic phonons in the presence of this coupling to the QPC, working to leading order in the electron–phonon interaction, and using scattering theory to calculate the QPC Keldysh Green functions. We then use these ‘dressed’ phonon Green functions to calculate the Fermi golden rule excitation rate of the DQD via the coupling described in equation (1). This excitation rate is finally incorporated into a master equation describing the occupation probability of the three relevant DQD states (Fig. 2c). In addition to the excitation rate (top panel of Fig. 2c), there is a rate Γfast describing the tunnelling from the excited state to the metastable auxiliary state (middle panel of Fig. 2c) and a rate Γslow describing the slow decay back to the true ground state (bottom panel of Fig. 2c). We take Γfast=1 GHz and Γslow=10 kHz; in this regime of Γfast≫Γslow, the non-ground state population of the DQD is independent of Γfast, whereas Γslow determines the overall magnitude of the interference oscillations. By using the master equation to calculate the stability diagram as a function of gate voltages, one can obtain the DQD charge susceptibility d(〈nR〉+ε〈nL〉)/dV L, which is proportional to the measured transconductance. The parameter ε∼0.4 characterizes the QPC’s asymmetric response to charge in the R versus L dot. Further details about the explicit form of λq,μ (including the role of screening and dimensionality) are provided in the Supplementary Information.
is described by scattering theory (see refs 8, 26). Note that as we are interested in a single-channel QPC, the spatial profile f(r) of the fluctuating QPC charge density is fixed; for simplicity, we take it to be a Gaussian of width rQPC. This fluctuating QPC charge density is coupled to acoustic phonons via the standard piezoelectric interaction (using parameters appropriate for GaAs (ref. 24)). We calculate the Keldysh Green functions of the acoustic phonons in the presence of this coupling to the QPC, working to leading order in the electron–phonon interaction, and using scattering theory to calculate the QPC Keldysh Green functions. We then use these ‘dressed’ phonon Green functions to calculate the Fermi golden rule excitation rate of the DQD via the coupling described in equation (1). This excitation rate is finally incorporated into a master equation describing the occupation probability of the three relevant DQD states (Fig. 2c). In addition to the excitation rate (top panel of Fig. 2c), there is a rate Γfast describing the tunnelling from the excited state to the metastable auxiliary state (middle panel of Fig. 2c) and a rate Γslow describing the slow decay back to the true ground state (bottom panel of Fig. 2c). We take Γfast=1 GHz and Γslow=10 kHz; in this regime of Γfast≫Γslow, the non-ground state population of the DQD is independent of Γfast, whereas Γslow determines the overall magnitude of the interference oscillations. By using the master equation to calculate the stability diagram as a function of gate voltages, one can obtain the DQD charge susceptibility d(〈nR〉+ε〈nL〉)/dV L, which is proportional to the measured transconductance. The parameter ε∼0.4 characterizes the QPC’s asymmetric response to charge in the R versus L dot. Further details about the explicit form of λq,μ (including the role of screening and dimensionality) are provided in the Supplementary Information.
References
Hanson, R., Kouwenhoven, L. P., Petta, J. R., Tarucha, S. & Vandersypen, L. M. K. Spins in few-electron quantum dots. Rev. Mod. Phys. 79, 1217–1265 (2007).
Fujisawa, T., Hayashi, T. & Sasaki, S. Time-dependent single-electron transport through quantum dots. Rep. Prog. Phys. 69, 759–796 (2006).
Petersson, K. D., Petta, J. R., Lu, H. & Gossard, A. C. Quantum coherence in a one-electron semiconductor charge qubit. Phys. Rev. Lett. 105, 246804 (2010).
Gaudreau, L. et al. Coherent control of three-spin states in a triple quantum dot. Nature Phys. 8, 54–58 (2011).
Field, M. et al. Coulomb blockade as a noninvasive probe of local density of states. Phys. Rev. Lett. 77, 350–353 (1996).
Elzerman, J. M. et al. Few-electron quantum dot circuit with integrated charge read out. Phys. Rev. B 67, 161308 (2003).
Aguado, R. & Kouwenhoven, L. P. Double quantum dots as detectors of high-frequency quantum noise in mesoscopic conductors. Phys. Rev. Lett. 84, 1986–1989 (2000).
Young, C. E. & Clerk, A. A. Inelastic back-action due to quantum point contact charge fluctuations. Phys. Rev. Lett. 104, 186803 (2010).
Khrapai, V. S., Ludwig, S., Kotthaus, J. P., Tranitz, H. P. & Wegscheider, W. Double-dot quantum ratchet driven by an independently biased quantum point contact. Phys. Rev. Lett. 97, 176803 (2006).
Taubert, D. et al. Telegraph noise in coupled quantum dot circuits induced by a quantum point contact. Phys. Rev. Lett. 100, 176805 (2008).
Gasser, U. et al. Statistical electron excitation in a double quantum dot induced by two independent quantum point contacts. Phys. Rev. B 79, 035303 (2009).
Schinner, G. J., Tranitz, H. P., Wegscheider, W., Kotthaus, J. P. & Ludwig, S. Phonon-mediated nonequilibrium interaction between nanoscale devices. Phys. Rev. Lett. 102, 186801 (2009).
Harbusch, D., Taubert, D., Tranitz, H. P., Wegscheider, W. & Ludwig, S. Phonon-mediated versus coulombic back-action in quantum dot circuits. Phys. Rev. Lett. 104, 196801 (2010).
Miller, A. & Abrahams, E. Impurity conduction at low concentrations. Phys. Rev. 120, 745–755 (1960).
Imry, Y. in Tunnelling Phenomena in Solids (eds Burstein, E. & Lundqvsit, S.) 563–576 (Plenum, 1969).
Brandes, T. Coherent and collective quantum optical effects in mesoscopic systems. Phys. Rep. 408, 315–474 (2005).
Fujisawa, T. et al. Spontaneous emission spectrum in double quantum dot devices. Science 282, 932–935 (1998).
Roulleau, P. et al. Coherent electron–phonon coupling in tailored quantum systems. Nature Commun. 2, 239 (2011).
Gaudreau, L. et al. Stability diagram of a few-electron triple dot. Phys. Rev. Lett. 97, 036807 (2006).
Schröer, D. et al. Electrostatically defined serial triple quantum dot charged with few electrons. Phys. Rev. B 76, 075306 (2007).
Rogge, M. C. & Haug, R. J. Two-path transport measurements on a triple quantum dot. Phys. Rev. B 77, 193306 (2008).
Rogge, M. C. & Haug, R. J. The three dimensionality of triple quantum dot stability diagrams. New J. Phys. 11, 113037 (2009).
Granger, G. et al. Three-dimensional transport diagram of a triple quantum dot. Phys. Rev. B 82, 075304 (2010).
Jasiukiewicz, C. Acoustic phonon emission by hot 2D electrons: The angular distribution of the emitted phonon power. Semicond. Sci. Technol. 13, 537–547 (1998).
Taubert, D., Schuh, D., Wegscheider, W. & Ludwig, S. Determination of energy scales in few-electron double quantum dots. Rev. Scient. Inst. 82, 123905 (2011).
Pedersen, M., van Langen, S. & Büttiker, M. Charge fluctuations in quantum point contacts and chaotic cavities in the presence of transport. Phys. Rev. B 57, 1838–1846 (1998).
Acknowledgements
S.L. and D. T. acknowledge financial support by the German Science Foundation via SFB 631, LU 819/4-1, and the German Excellence Initiative via the ‘Nanosystems Initiative Munich’ (NIM). G.G. acknowledges funding from the NRC–CNRS collaboration. A.S.S. and A.A.C. acknowledge funding from NSERC and CIFAR.
Author information
Authors and Affiliations
Contributions
D.T. fabricated the DQD samples, performed the DQD experiments and analysed the data. D.H. performed preliminary experiments on another DQD sample. A.K. fabricated the TQD sample. L.G., G.G. and S.S. performed the TQD experiments and analysed the data. P.Z. assisted in these experiments. D.S. and W.W. grew the heterostructures for the DQD samples; Z.R.W. optimized and grew the heterostructure for the TQD sample. D.T., L.G., C.E.Y., A.A.C., A.S.S. and S.L. wrote the paper. C.E.Y. and A.A.C. developed the theoretical model and supported both experimental groups. A.S.S. and S.L. supervised the experimental collaboration from Ottawa and Munich. The experiments have been supervised collaboratively by A.S.S. and S.L.; the theoretical modelling was surpervised by A.A.C.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Information (PDF 652 kb)
Rights and permissions
About this article
Cite this article
Granger, G., Taubert, D., Young, C. et al. Quantum interference and phonon-mediated back-action in lateral quantum-dot circuits. Nature Phys 8, 522–527 (2012). https://doi.org/10.1038/nphys2326
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys2326
This article is cited by
-
Hyperfine-phonon spin relaxation in a single-electron GaAs quantum dot
Nature Communications (2018)
-
Engineering the quantum-classical interface of solid-state qubits
npj Quantum Information (2015)
-
Formation of a protected sub-band for conduction in quantum point contacts under extreme biasing
Nature Nanotechnology (2014)
-
Quantum strain sensor with a topological insulator HgTe quantum dot
Scientific Reports (2014)
-
Raman phonon emission in a driven double quantum dot
Nature Communications (2014)