Abstract
When an electron moves in a smoothly varying non-collinear magnetic structure, its spin orientation adapts constantly, thereby inducing forces that act both on the magnetic structure and on the electron. These forces may be described by electric and magnetic fields of an emergent electrodynamics1,2,3,4. The topologically quantized winding number of so-called skyrmions—a type of magnetic whirl discovered recently in chiral magnets5,6,7—has been predicted to induce exactly one quantum of emergent magnetic flux per skyrmion. A moving skyrmion is therefore expected to induce an emergent electric field following Faraday’s law of induction, which inherits this topological quantization8. Here we report Hall-effect measurements that establish quantitatively the predicted emergent electrodynamics. We obtain quantitative evidence for the depinning of skyrmions from impurities (at current densities of only 106 A m−2) and their subsequent motion. The combination of exceptionally small current densities and simple transport measurements offers fundamental insights into the connection between the emergent and real electrodynamics of skyrmions in chiral magnets, and might, in the long term, be important for applications.
Similar content being viewed by others
Main
Skyrmion lattice phases (SLPs) in chiral magnets such as MnSi and other B20 transition metal compounds are a new form of magnetic order, composed of topologically protected vortex lines (the skyrmions) with a non-zero winding number which are stabilized parallel to a small applied magnetic field. Skyrmion lattices in magnetic materials were discovered only recently by means of small angle neutron scattering (SANS; refs 5, 9). The winding number of the spin structure was thereby first inferred from topological contributions to the Hall effect6 and Lorentz force microscopy for thin samples, where the latter even established the existence of individual skyrmions7. So far, SLPs have been identified in all non-centrosymmetric B20 transition metal compounds that order helimagnetically at zero magnetic field, regardless of whether they are pure metals, strongly doped semiconductors or even insulators5,10,11. The excellent theoretical understanding implies that skyrmions are a general phenomenon to be expected in a wide range of bulk materials as well as nanoscale systems5,7,12, with the identification of spontaneous skyrmion lattices in monatomic layers of iron on an iridium substrate being a major new development13.
Exploratory SANS studies14 revealed a rotation of the diffraction pattern in the SLP of single-crystal MnSi when an electric current applied transverse to the skyrmions exceeded an ultralow threshold of jc∼106 A m−2. It is therefore important to emphasize that jc is 105 times smaller than the currents needed to induce a motion in present-day spin-torque experiments on ferromagnetic domain walls15,16,17. However, the rotation occurred only in the presence of a small temperature gradient (∼1 K cm−1), inducing gradients in the relevant forces, which in turn caused rotational torques. It was argued that above the critical current density, jc, the skyrmions start to move and that only the sliding skyrmions can be rotated by the tiny torques. Although microscopic probes such as neutron scattering and Lorentz force microscopy may in principle confirm the depinning and motion of the skyrmions, they are not capable of detecting the emergent electrodynamics. Instead, to detect the motion of the skyrmions, measurements of the emergent electric fields are ideally suited, because they are directly proportional to their velocity. This may be readily achieved by means of the Hall effect.
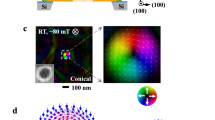
The magnetic properties of MnSi are governed by a combination of ferromagnetic exchange interactions and weak spin–orbit coupling in the absence of inversion symmetry. At zero magnetic field MnSi exhibits a paramagnetic-to-helimagnetic transition at Tc≈28.5 K. In a small range of fields and temperatures below Tc the SLP is stabilized5, where the skyrmions (the magnetic whirls) form a hexagonal lattice perpendicular to the applied magnetic field. The lattice constant  of the skyrmion lattice, determined from the reciprocal lattice vectors, is set by the wavelength of the helimagnetic state, λhelix∼180 Å.
of the skyrmion lattice, determined from the reciprocal lattice vectors, is set by the wavelength of the helimagnetic state, λhelix∼180 Å.
Our study of the influence of electric current on the SLP was carried out on high-purity single crystals using a standard six-terminal lock-in technique (see Methods for details). Shown in Fig. 1a are typical temperature dependences of the Hall resistivity, ρx y, for small currents (black curves). Its dominant features arise from the temperature dependence of the anomalous Hall effect. The small maximum in ρx y is therefore a characteristic of the magnetization at the lower boundary of the SLP above a narrow regime of phase coexistence between the conical phase and the SLP (ref. 18). Also shown in Fig. 1a is the Hall resistivity under an applied d.c. current density of j=2.81×106 A m−2, where a suppression (marked in light blue shading) is observed in the temperature range marked by the black arrows. The latter is in excellent agreement with the phase boundaries of the SLP as inferred from the magnetization and susceptibility. The size of the suppression of the Hall signal is similar to the topological Hall contribution Δρx y≈4 nΩ cm previously inferred6 from Hall effect measurements at small currents (see Supplementary Information).
To study the effect of the applied d.c. current it is superimposed on a small a.c. excitation which allows detection of the signal. a, Hall resistivity for various magnetic fields. Under an applied d.c. current of 2.81×106 A m−2 the Hall signal is suppressed in the entire skyrmion phase (blue shading). b, Hall resistivity in the SLP for an applied magnetic field B=250 mT under selected applied d.c. currents between j=0 and j=2.81×106 A m−2.
Detailed Hall data for an applied magnetic field of 0.25 T and a wide range of applied d.c. currents, j, are shown in Fig. 1b. From these the evolution of ρx y with applied electric current density was inferred for selected temperatures, as shown in Fig. 2. At temperatures outside the SLP, shown in Fig. 2a,e, the Hall signal is unchanged as a function of j. Within the SLP, ρx y is unchanged within the experimental accuracy for small current densities, j<jc, followed by a clear decrease above jc over a finite range of applied currents (light blue shading), which then saturates for even larger currents (the method by which jc was determined is described in Supplementary Information).
For temperatures in the skyrmion lattice phase, those shown in b–d, the signal is suppressed above an ultralow current density, jc, and converges towards a constant value for large currents. Absolute data values are given on the left-hand side and the relative change with respect to j=0 is given on the right-hand side. Error bars represent the statistical error of the data after subtracting a spline fit.
Shown in Fig. 3a is the critical current density as a function of temperature, where jc∼106 A m−2 agrees within a factor of two with the onset of the rotation of the scattering pattern observed in the SANS study14. As discussed in ref. 14, the exceptionally low value of jc arises from a combination of several factors: first, the very efficient Berry-phase coupling between conduction electrons and the spin structure; second, because of the smooth variation of the magnetization the skyrmion lattice couples only weakly to defects and the atomic crystal structure; and third, the long range stiffness and crystalline character of the skyrmion lattice9 leads to a partial cancellation of the pinning forces19,20. The value of jc grows by roughly a factor of two when approaching the (first order) transition to the weakly field-polarized paramagnetic state. At the same time the suppression of ρx y given by  is greatest in the centre of the skyrmion phase, with a gradual decrease at the lower boundary (see Fig. 3b).
is greatest in the centre of the skyrmion phase, with a gradual decrease at the lower boundary (see Fig. 3b).
a, Temperature dependence of the critical current density, jc. The label on the right axis gives an estimate of the pinning velocity, see equation (6). b, Total change of the Hall resistivity for large currents,  , as a function of temperature. c, Scaling plot of the transverse electric field,
, as a function of temperature. c, Scaling plot of the transverse electric field,  , in units of
, in units of  , induced by the moving skyrmion lattice. As
, induced by the moving skyrmion lattice. As  is proportional to the emergent field Ee, this also constitutes a scaling plot of the emergent electric field Ee (in units of vpinBe) or of the drift velocity
is proportional to the emergent field Ee, this also constitutes a scaling plot of the emergent electric field Ee (in units of vpinBe) or of the drift velocity  in units of the pinning velocity vpin (shown in a). Unscaled data used to construct c are shown in the Supplementary Information. Error bars represent the statistical error of the data after subtracting a spline fit.
in units of the pinning velocity vpin (shown in a). Unscaled data used to construct c are shown in the Supplementary Information. Error bars represent the statistical error of the data after subtracting a spline fit.
To address our observations on ρx y from a theoretical point of view we note that the forces driving the skyrmion lattice, which also cause the topological contribution to the Hall signal, originate in quantum-mechanical phases (Berry phases) picked up by electrons when their spin follows the orientation  of the local magnetization M. The Berry phase can be rewritten1,8,21 as an effective Aharonov–Bohm phase, associated with ‘emergent’ magnetic and electric fields, Be and Ee. As the Berry phase is given by the solid angle covered by
of the local magnetization M. The Berry phase can be rewritten1,8,21 as an effective Aharonov–Bohm phase, associated with ‘emergent’ magnetic and electric fields, Be and Ee. As the Berry phase is given by the solid angle covered by  , the emergent fields Be and Ee measure the solid angle for an infinitesimal loop in space and space–time, respectively
, the emergent fields Be and Ee measure the solid angle for an infinitesimal loop in space and space–time, respectively

with ∂i=∂/∂ ri, ∂t=∂/∂ t, and εi j k is the totally antisymmetric tensor. Because the sign of the Berry phase depends on the spin orientation, a majority spin with magnetization parallel to  carries the emergent charge q↓e=−1/2 whilst a minority spin carries the emergent charge q↑e=+1/2. For a skyrmion, defined as a magnetic whirl where
carries the emergent charge q↓e=−1/2 whilst a minority spin carries the emergent charge q↑e=+1/2. For a skyrmion, defined as a magnetic whirl where  winds once around the unit sphere in the plane perpendicular to B (while
winds once around the unit sphere in the plane perpendicular to B (while  does not vary in the spatial direction longitudinal to B), the total ‘emergent flux’ is given by
does not vary in the spatial direction longitudinal to B), the total ‘emergent flux’ is given by  . It is hence topologically quantized to one flux quantum −2πℏ/|qe| per skyrmion (the sign accounts for the formation of antiskyrmions in MnSi; ref. 5). Further, according to equation (1) and in complete analogy to Faraday’s law of induction, a skyrmion lattice drifting with velocity vdmust induce an electric field Ee=−vd×Be, where Ee/|vd|inherits its quantization from Be with Ee=|Ee| and Be=|Be|. This topological quantization of Be and Ee makes skyrmion lattices in metals an ideal system to study quantitatively the emergent electrodynamics underlying the coupling of charge and magnetism8. In MnSi, the emergent magnetic field acquires an average strength of 2.5 T, that is Be≈2.5 T|e/qe|, where e is the electron charge.
. It is hence topologically quantized to one flux quantum −2πℏ/|qe| per skyrmion (the sign accounts for the formation of antiskyrmions in MnSi; ref. 5). Further, according to equation (1) and in complete analogy to Faraday’s law of induction, a skyrmion lattice drifting with velocity vdmust induce an electric field Ee=−vd×Be, where Ee/|vd|inherits its quantization from Be with Ee=|Ee| and Be=|Be|. This topological quantization of Be and Ee makes skyrmion lattices in metals an ideal system to study quantitatively the emergent electrodynamics underlying the coupling of charge and magnetism8. In MnSi, the emergent magnetic field acquires an average strength of 2.5 T, that is Be≈2.5 T|e/qe|, where e is the electron charge.
The total force on an electron with momentum k and spin orientation σ is therefore given8 by

where vσ k n is the velocity of quasiparticles in band n, Eis the physical electrical field and |FH|≪e|E| is the Hall force from the normal and anomalous Hall effect. Further dissipative drag forces, Fdiss, arising for  are probably much smaller (see Supplementary Information). The extra electric current induced by −qσevd×Be transverse to the electrical current has to be cancelled exactly by the change of the electric Hall field
are probably much smaller (see Supplementary Information). The extra electric current induced by −qσevd×Be transverse to the electrical current has to be cancelled exactly by the change of the electric Hall field  , with Δρx y=ρx y(j)−ρx y(0). For a current in the x direction and a magnetic field in z direction we find using equation (2)
, with Δρx y=ρx y(j)−ρx y(0). For a current in the x direction and a magnetic field in z direction we find using equation (2)


where the dimensionless spin polarization  can be obtained by calculating the cross-correlation of the charge current j and the emergent current je using Kubo formulae.
can be obtained by calculating the cross-correlation of the charge current j and the emergent current je using Kubo formulae.  is the ratio of electric currents obtained from Ee and E, where a simple approximation for
is the ratio of electric currents obtained from Ee and E, where a simple approximation for  is given in equation (4) in the relaxation time approximation of a multiband system (fn σ0is the Fermi distribution for band n with scattering rate 1/τσ n and spin-orientation σ relative to the local magnetization). Up to the factor
is given in equation (4) in the relaxation time approximation of a multiband system (fn σ0is the Fermi distribution for band n with scattering rate 1/τσ n and spin-orientation σ relative to the local magnetization). Up to the factor  , the measurement of the Hall field is therefore a direct measurement of the emergent field Ee and of vd=Ee/Be, as Be is quantized.
, the measurement of the Hall field is therefore a direct measurement of the emergent field Ee and of vd=Ee/Be, as Be is quantized.
The drift velocity along the current direction, vd∥, in absolute units is obtained from equation (3)


Here we used  in the centre of the skyrmion phase and estimated the effective polarization to be
in the centre of the skyrmion phase and estimated the effective polarization to be  (ref. 6). We further used that
(ref. 6). We further used that  is approximately independent of the local magnetization and therefore of the temperature. As expected, the corresponding pinning velocities (see labels on the right axes in Fig. 3a) are of the same order of magnitude as the electronic drift velocities, vdrift∼j/e n≈0.16 mm s−1 for j∼jc∼106 A m−2, where we estimate n≈3.8 ×1022 cm−3 from the normal Hall constant6. The expression 4πℏM vpin may finally be interpreted as the force per skyrmion and per length needed to depin the SLP (see Supplementary Information).
is approximately independent of the local magnetization and therefore of the temperature. As expected, the corresponding pinning velocities (see labels on the right axes in Fig. 3a) are of the same order of magnitude as the electronic drift velocities, vdrift∼j/e n≈0.16 mm s−1 for j∼jc∼106 A m−2, where we estimate n≈3.8 ×1022 cm−3 from the normal Hall constant6. The expression 4πℏM vpin may finally be interpreted as the force per skyrmion and per length needed to depin the SLP (see Supplementary Information).
The critical current and the pinning velocities grow by a factor of two just below the first-order transition Tpc, see Fig. 3a. This cannot be explained by the decrease of the local magnetization (proportional to the small drop in  ). Instead, the increase of jc most probably reflects the reduction of the stiffness of the skyrmion lattice when approaching Tpc, which is only a very weak first-order phase transition. With decreasing stiffness the skyrmion lattice adjusts better to the disorder potential, implying that the pinning forces increase substantially19,22,23. Consistent with this picture, there is essentially no temperature dependence of jc at the low-temperature side of the SLP, where the phase transition is strongly first order. Here
). Instead, the increase of jc most probably reflects the reduction of the stiffness of the skyrmion lattice when approaching Tpc, which is only a very weak first-order phase transition. With decreasing stiffness the skyrmion lattice adjusts better to the disorder potential, implying that the pinning forces increase substantially19,22,23. Consistent with this picture, there is essentially no temperature dependence of jc at the low-temperature side of the SLP, where the phase transition is strongly first order. Here  shows a gradual temperature dependence in the range from 25.8 K to 26.5 K that may be attributed to the phase coexistence between the conical phase and the skyrmion phase as inferred from high-precision magnetometry18.
shows a gradual temperature dependence in the range from 25.8 K to 26.5 K that may be attributed to the phase coexistence between the conical phase and the skyrmion phase as inferred from high-precision magnetometry18.
Combining the results of our analysis, we show in Fig. 3c a scaling plot of  , or equivalently of the parallel drift velocity
, or equivalently of the parallel drift velocity  of equation (5) and the associated emergent electric field
of equation (5) and the associated emergent electric field  , as a function of j/jc. To obtain quantitative values for
, as a function of j/jc. To obtain quantitative values for  and
and  in physical units, one may refer to Fig. 3a, equation (6), and
in physical units, one may refer to Fig. 3a, equation (6), and  with Be=2.5 T|e/qe|.
with Be=2.5 T|e/qe|.
For j<jc, the drift velocity vanishes within our experimental precision, as the skyrmion lattice is pinned by disorder. For j>jc, the Magnus forces are sufficiently strong to overcome the pinning forces and the skyrmions start to move. For j≫jc their velocity becomes proportional to the current, as pinning forces can be neglected. This is precisely the picture that has been developed for the depinning transition of charge density waves and vortices19,20,22,23. However, the precise behaviour of skyrmions differs from that of vortices because their dynamics is very different. Because of their strong friction, superconducting vortices flow approximately perpendicular to the current following the Magnus force and the resulting Hall signals are tiny22,24. In contrast, skyrmions drift dominantly parallel to j, thus reducing the relative speed of spin current and giving rise to a large Faraday field in the perpendicular direction. A more technical discussion of the validity of the scaling, the forces on the SLP and its direction of motion is given in Supplementary Information.
The direct observation of the emergent electric field of skyrmions reported in this paper allowed us to measure their depinning transition and subsequent motion quantitatively. This opens the possibility to address fundamental questions of the coupling of magnetism, electric currents and defects, respectively. The control and detection of the motion of magnetic whirls (skyrmions) by the interplay of emergent and real electrodynamics therefore promises to become an important route towards spintronic applications.
Methods
Sample preparation.
Single crystals of MnSi were grown by optical float-zoning under ultrahigh-vacuum-compatible conditions25. The specific heat, susceptibility, and resistivity of small pieces taken from this single crystal were in excellent agreement with the literature, where the residual resistivity ratio was of the order 100. This indicates good, although not excellent sample purity. The sample quality was the same as for the samples studied in the SANS experiments reported in ref. 14. Samples for the measurements reported here were oriented by Laue X-ray diffraction, cut with a wire saw, and carefully polished to size. Current leads were soldered to the small faces of the sample and Au wires for the voltage pick-up were spot-welded onto the surface of the sample. All data reported in this paper were recorded for a magnetic field parallel to the 〈100〉 axis and electric current parallel to the 〈110〉 axis.
Spin-torque transport.
For our measurements of the Hall and longitudinal resistivity we modified a standard six-terminal phase-sensitive detection system such that large d.c. currents could be superimposed on a small a.c. excitation. The set-up is based on a method used for measurements of superconducting tunnel junctions26. It was tested on high-purity Cu to ensure proper operation. In all experiments the a.c. excitation amplitudes were not larger than a few per cent of the applied d.c. currents. The samples were carefully anchored to the cryogenic system to minimize ohmic heating and temperature gradients. In particular, compared with the SANS experiments reported in ref. 14, all thermal gradients were minimized. The Hall signal and the longitudinal resistivity, ρx y and ρx x, respectively, were measured simultaneously at a low excitation frequency of 22.5 Hz. To correct for the remaining tiny amount of uniform ohmic heating, which generated a small systematic temperature difference between the sample and thermometer of less than a few tenths of a kelvin for the largest currents applied, we calculated from the longitudinal resistivity ρx x the true sample temperature. However, we have tested carefully that our results do not depend on the precise way in which these small ohmic heating effects are corrected.
References
Volovik, G. Linear momentum in ferromagnets. J. Phys. C 20, L87 (1987).
Yang, S. A. et al. Universal electromotive force induced by domain wall motion. Phys. Rev. Lett. 102, 067201 (2009).
Hai, P. N., Ohya, S., Tanaka, M., Barnes, S. E. & Maekawa, S. Electromotive force and huge magnetoresistance in magnetic tunnel junctions. Nature 458, 489–492 (2009).
Barnes, S. E. & Maekawa, S. Generalization of Faraday’s law to include nonconservative spin forces. Phys. Rev. Lett. 98, 246601 (2007).
Mühlbauer, S. et al. Skyrmion lattice in a chiral magnet. Science 323, 915–919 (2009).
Neubauer, A. et al. Topological Hall effect in the A phase of MnSi. Phys. Rev. Lett. 102, 186602 (2009).
Yu, X. Z. et al. Real-space observation of a two-dimensional skyrmion crystal. Nature 465, 901–904 (2010).
Zang, J., Mostovoy, M., Han, J. H. & Nagaosa, N. Dynamics of skyrmion crystals in metallic thin films. Phys. Rev. Lett. 107, 136804 (2011).
Adams, T. et al. Long-range crystalline nature of the skyrmion lattice in MnSi. Phys. Rev. Lett. 107, 217206 (2011).
Münzer, W. et al. Skyrmion lattice in the doped semiconductor Fe1−xCoxSi. Phys. Rev. B (R) 81, 041203 (2010).
Pfleiderer, C. et al. Skyrmion lattices in metallic and semiconducting B20 transition metal compounds. J. Phys. Condens. Matter 22, 164207 (2010).
Bogdanov, A. N. & Yablonskii, D. A. Thermodynamically stable ‘vortices’ in magnetically ordered crystals. The mixed state of magnets. Sov. Phys. JETP 68, 101–103 (1989).
Heinze, S. et al. Spontaneous atomic-scale magnetic skyrmion lattice in two dimensions. Nature Phys. 7, 713–718 (2011).
Jonietz, F. et al. Spin transfer torques in MnSi at ultra-low current densities. Science 330, 1648–1651 (2010).
Grollier, J. et al. Switching a spin valve back and forth by current-induced domain wall motion. Appl. Phys. Lett. 83, 509–511 (2003).
Tsoi, M., Fontana, R. & Parkin, S. Magnetic domain wall motion triggered by an electric current. Appl. Phys. Lett. 83, 2617–2619 (2003).
Yamanouchi, M., Chiba, D., Matsukura, F. & Ohno, H. Current-induced domain-wall switching in a ferromagnetic semiconductor structure. Nature 428, 539–542 (2004).
Bauer, A. et al. Quantum phase transitions in single-crystal Mn1−xFexSi and Mn1−xCoxSi: Crystal growth, magnetization, ac susceptibility, and specific heat. Phys. Rev. B 82, 64404 (2010).
Larkin, A. I. & Ovchinnikov, Y. N. Electrodynamics of inhomogeneous type-II superconductor. Sov. Phys. JETP 38, 854–858 (1974).
Schmid, A. & Hauger, W. On the theory of vortex motion in an inhomogeneous superconducting film. J. Low Temp. Phys. 11, 667–685 (1973).
Zhang, S. & Zhang, S. S-L. Generalization of the Landau–Lifshitz–Gilbert equation for conducting ferromagnets. Phys. Rev. Lett. 102, 086601 (2009).
Blatter, G., Feigel’man, M. V., Geshkenbein, V. B., Larkin, A. I. & Vinokur, V. M. Vortices in high-temperature superconductors. Rev. Mod. Phys. 66, 1125–1388 (1994).
Brazovskii, S. & Nattermann, T. Pinning and sliding of driven elastic systems: Domain walls and charge density waves. Adv. Phys. 53, 177–253 (2004).
Kopnin, N. Vortex dynamics and mutual friction in superconductors and Fermi superfluids. Rep. Prog. Phys. 65, 1633–1678 (2002).
Neubauer, A. et al. Ultra-high vacuum compatible image furnace. Rev. Sci. Instrum. 82, 013902 (2010).
Welter, B. Tunnelspektroskopie an Korngrenzenkontakten aus elektronendotierten Hochtemperatur–Supraleitern. PhD thesis, Technische Univ. München (2007).
Acknowledgements
We wish to thank P. Böni, H. Hagn, N. Nagaosa, T. Nattermann, S. Mayr, M. Opel, B. Russ, B. Spivak, G. Stölzl and V. M. Vinokur for helpful discussions and support. R.R., A.B., M.W. and C.F. acknowledge financial support through the TUM Graduate School. K.E. acknowledges financial support through the Deutsche Telekom Stiftung and the Bonn Cologne Graduate School. Financial support through Deutsche Forschungsgemeinschaft TRR80, SFB608 and FOR960 is gratefully acknowledged.
Author information
Authors and Affiliations
Contributions
T.S., R.R. M.H., M.W. and C.P. developed the experimental set-up; T.S. and R.R. performed the experiments; T.S., R.R. and C.P. analysed the experimental data; C.F. wrote the software for analysing the data; A.B. grew the single-crystal samples and characterized them; K.E., M.G. and A.R. developed the theoretical interpretation; C.P. supervised the experimental work; C.P. and A.R. proposed this study and wrote the manuscript; all authors discussed the data and commented on the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Information (PDF 1113 kb)
Rights and permissions
About this article
Cite this article
Schulz, T., Ritz, R., Bauer, A. et al. Emergent electrodynamics of skyrmions in a chiral magnet. Nature Phys 8, 301–304 (2012). https://doi.org/10.1038/nphys2231
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys2231
This article is cited by
-
Ordered creation and motion of skyrmions with surface acoustic wave
Nature Communications (2023)
-
Transition between distinct hybrid skyrmion textures through their hexagonal-to-square crystal transformation in a polar magnet
Nature Communications (2023)
-
Bloch points and topological dipoles observed by X-ray vector magnetic tomography in a ferromagnetic microstructure
Communications Physics (2023)
-
Topological magneto-optical effect from skyrmion lattice
Nature Communications (2023)
-
Machine learning assisted derivation of minimal low-energy models for metallic magnets
npj Computational Materials (2023)