Experimental investigation of the entanglement-assisted entropic uncertainty principle

Abstract

The uncertainty principle, which bounds the uncertainties involved in obtaining precise outcomes for two complementary variables defining a quantum particle, is a crucial aspect in quantum mechanics. Recently, the uncertainty principle in terms of entropy has been extended to the case involving quantum entanglement¹. With previously obtained quantum information for the particle of interest, the outcomes of both non-commuting observables can be predicted precisely, which greatly generalizes the uncertainty relation. Here, we experimentally investigated the entanglement-assisted entropic uncertainty principle for an entirely optical set-up. The uncertainty is shown to be near zero in the presence of quasi-maximal entanglement. The new uncertainty relation is further used to witness entanglement. The verified entropic uncertainty relation provides an intriguing perspective in that it implies the uncertainty principle is not only observable-dependent but is also observer-dependent².

Main

In quantum mechanics, the outcomes of an observable can be predicted precisely by preparing eigenvectors corresponding to the state of the measured system. However, the ability to predict the precise outcomes of two conjugate observables for a particle is restricted by the uncertainty principle. Originally observed by Heisenberg³, the uncertainty principle is best known as the Heisenberg–Robertson commutation⁴

where ΔR (ΔS) represents the standard deviation of the corresponding variable R (S). It can be seen that the bound on the right-hand side is state-dependent and can vanish even when R and S are non-commuting. To avoid this defect, the uncertainty relation has been re-derived in terms of an information-theoretic model⁵ in which the uncertainty relating to the outcomes of the observable is characterized by the Shannon entropy instead of the standard deviation. The entropic uncertainty relation for any two general observables was first given by Deutsch⁶. Soon afterwards, an improved version was proposed by Kraus⁷ and then proved by Maassen and Uiffink⁸. The improved relation reads as follows:

where H is the Shannon entropy, c=max_i,j|〈a_i|b_j〉|² and represents the overlap between observables R and S, and |a_i〉 (|b_j〉) represents the eigenvectors of R (S).

Although we cannot obtain the precise outcomes of both the two conjugate variables, even when the density matrix of the prepared state is known, the situation would be different if we invoked the effect of quantum entanglement. The possibility of violating the Heisenberg–Robertson uncertainty relation was identified early by Einstein, Podolsky, and Rosen in their famous paper, and was originally used to challenge the correctness of quantum mechanics (EPR paradox)⁹. Popper also proposed a practical experiment¹⁰ to demonstrate the violation of the Heisenberg–Robertson uncertainty relation, which has since been experimentally realized¹¹. The gedanken experiment for the EPR paradox was further exploited^12,13 and experimentally demonstrated¹⁴. At present, the violation of uncertainty relations is implemented as a signature of entanglement¹⁵ and is used to study the continuous variable entanglement^16,17.

However, the previous experimental tests were restricted to non-entropic uncertainty relations, where, crucially, the information about the initial state is purely classical. More recently, a stronger entropic uncertainty relation, which uses previously determined quantum information, was proved by Berta et al.¹, the equivalent form of which was previously conjectured by Renes and Boileau¹⁸. By initially entangling the particle of interest (A) to another particle that acts as a quantum memory (B), the uncertainty associated with the outcomes of two conjugate observables can be drastically reduced to an arbitrarily small value. The entropic uncertainty relation is mathematically expressed as follows¹

where H(R|B) (H(S|B)) is the conditional von Neumann entropy representing the uncertainty of the measurement outcomes of R (S) obtained using the information stored in B. H(A|B) represents the conditional von Neumann entropy between A and B. It is known that −H(A|B) gives the lower bound of the one-way distillable entanglement¹⁹. As a result, the lower bound of the uncertainty is essentially dependent on the entanglement between A and B.

In this paper, we report an experimental investigation of the new entropic uncertainty principle in a completely optical set-up. This study differs from earlier related works that were mainly intended to show a violation of the classical uncertainty relation. The entropic uncertainty relation is used to witness entanglement¹. We further change the complementarity of the two measured observables and verify the new uncertainty relation (1) with the particle B stored in a spin-echo based quantum memory.

We first choose to measure two Pauli observables, R=σ_x and S=σ_z, to investigate the new entropic uncertainty principle. The photon of interest A is then prepared for entanglement with another photon B through the form of Bell diagonal states (BDS)

where and are the Bell states, and x represents the corresponding ratio between these two components in ρ₁ (the calculation of the corresponding conditional entropies is given in Methods).

To use the entropic uncertainty relation (1) to witness entanglement, we follow the same procedure, using observables R=σ_x (S=σ_z) on both particles A and B. The variable d_R represents the probability that the outcomes of R on A and R on B are different, and d_S represents the probability that the outcomes of S on A and S on B are different. According to Fano’s inequality relation²⁰,

where h(d_R)=−d_Rlog₂d_R−(1−d_R)log₂(1−d_R). As a result, when h(d_R)+h(d_S)−1<0, H(A|B)<0, according to the inequality (1), which indicates the entanglement between A and B.

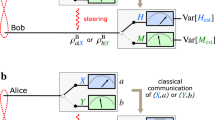
In our experiment, the polarizations of photons are encoded as information carriers. We set the horizontal polarization state (|H〉) as |0〉and the vertical polarization state (|V〉) as |1〉. Figure 1 shows the experimental set-up. Ultraviolet pulses with a 76 MHz repetition rate (wavelength centred at 400 nm) are focused on two type-I β-barium borate crystals to generate polarization-entangled photon pairs²¹, which are emitted into modes A and B (for simplicity, we just refer to photons A and B). After compensating the birefringence using quartz plates, the maximally entangled state is prepared with high visibility²². To prepare different kinds of BDS, photon B further passes through an unbalanced Mach–Zehnder interference (UMZ) set-up. The time difference between the short and long paths of the UMZ is about 1.5 ns, which is smaller than the coincidence window. By tracing over the path information in the UMZ (ref. 23), the BDS described by equations (2) (ρ₁) can be produced. The density matrix of the initial BDS is characterized by the quantum state tomography process²⁴, in which H(A|B)can be calculated. To measure H(R|B) and H(S|B), the measurement apparatus M, containing two half-wave plates (HWPs) and a polarization beam splitter (PBS), is applied to the photon A. After passing through M, photon A is sent to the polarization analysis measurement device, together with photon B, for quantum state tomography. The spin-echo based quantum memory operation, consisting of two polarization maintaining (PM) fibres, each of 120 m length, and two HWPs, with the angles set at 45°, is performed on mode B, depending on the specific case. The polarization analysis measurement set-up, containing quarter-wave plates (QWPs), HWPs and a PBS, can be used to perform corresponding observable measurements on both the photons as well as the tomographic measurement. These two photons are then detected by two single-photon detectors (SPDs), equipped with 3 nm interference filters (IFs), in which the measured quantities are based on coincident counts.

Figure 1: Experimental setup.

Ultraviolet pulses pass through two type-I β-barium borate (BBO) crystals to produce polarization-entangled photon pairs, which are emitted into modes A and B. Quartz plates (CP) are used to compensate the birefringence of the BBO crystals. The photon in mode B further passes through a UMZ set-up to prepare the required BDS. The attenuators (ATT) are used to control the ratio between different components in the BDS. Quarter-wave plates (QWPs) and half-wave plates (HWPs) are employed to prepare the exact forms of the BDS. The dashed section M, containing two HWPs and a polarization beam splitter (PBS), is used to measure R and S on the photon A. With the optic axes of the two HWPs set to θ/2 and θ/2−45° respectively, M projects the corresponding state of photon Aonto the two eigenvectors cosθ|H〉+sinθ|V〉 and sinθ|H〉−cosθ|V〉. The quantum memory operation, which consists of two polarization-maintaining (PM) fibres 120 m length in length, and two HWPs (FC represents the fibre coupler), is performed on the photon in mode B, depending on the specific case. The polarization analysis measurement device, containing a QWP, HWP and PBS in each arm, is used to perform observable measurements on both the photons as well as the tomographic measurement. Both photons are then detected by single-photon detectors (SPDs) equipped with 3 nm interference filters (IFs). When the quantum memory operation is performed on mode B, the detected signal in mode A is delayed by approximately 1.2 μs, such that it coincides with that in mode B in the coincidence counting circuit (not shown).

Figure 2 shows the experimentally determined uncertainties when measuring the outcomes of σ_x and σ_z on photon A, which is entangled with another photon B. Red circles and black squares represent the experimental results of H(σ_x|B)+H(σ_z|B) and 1+H(A|B), with the red and black solid lines representing the corresponding theoretical predictions, respectively. It is clear that 1+H(A|B) provides a lower bound of uncertainties when obtaining the outcomes of both σ_x and σ_z, and the experimental results agree well with the theoretical predictions within the error bars. We also considered a further case in which the prepared state is a different kind of BDS to show the state-dependent behaviour of the entropic relation (1) (see Supplementary Fig. S1).

Figure 2: Experimental results for the conditional entropies with the input state ρ₁.

The xaxis represents the amount of |ϕ⁺〉 in ρ₁. Red circles represent the experimental results for H(σ_x|B)+H(σ_z|B) and black squares denote the results of 1+H(A|B). The red and black solid lines are the corresponding theoretical predictions, respectively. The state at the point x=0.5 is the maximally mixed state without entanglement, where H(σ_x|B)+H(σ_z|B)becomes maximal. At the points near x=0 and x=1, where photon Ais quasi-maximally entangled to B, the lower bound of 1+H(A|B)is near zero, and the uncertainty of H(σ_x|B)+H(σ_z|B) is close to this value, within the error bars. Error bars represent the corresponding standard deviations.

Next, we use the entropic uncertainty relation of inequality (1) to witness entanglement. Figure 3 shows the experimental results. The red circles represent the experimental results of h($d_{{\sigma }_x}$)+h($d_{{\sigma }_y}$)−1, and the red solid line represents the corresponding theoretical prediction (see Methods for its calculation). The cases with h($d_{{\sigma }_x}$)+h($d_{{\sigma }_z}$)−1<0 indicate a one-way distillable entanglement between A and B (ref. 19). The blue solid line represents the constant zero. The green stars denote the theoretically calculated value of h($d_{{\sigma }_x}$)+h($d_{{\sigma }_z}$)−1 from the experimentally measured density matrix of ρ₁, which agrees with the experimental results. The entanglement between A and B is further measured by the concurrence²⁵ represented by the black squares, and the black solid line represents the theoretical prediction (see Methods). We can see from Fig. 3 that the value of h($d_{{\sigma }_x}$)+h($d_{{\sigma }_z}$)−1 witnesses the lower bounds of entanglement shared between A and B. The concurrence calculated from the reconstructed density matrix requires quantum state tomography with nine measurement settings, whereas the approach using the uncertainty relation to witness entanglement requires only two measurement settings. Thus, this new uncertainty relation would find practical use in the area of quantum engineering.

Figure 3: Experimental results for the entanglement witness using the input state of ρ₁.

The xaxis represents the amount of |ϕ⁺〉 in ρ₁. The red circles represent the experimental results for h($d_{{\sigma }_x}$)+h($d_{{\sigma }_z}$)−1, and the red solid line represents the theoretical prediction. h($d_{{\sigma }_x}$)+h($d_{{\sigma }_z}$)−1<0 when x<0.11 and x>0.89. The blue solid line represents the constant zero. The green stars are the values of h($d_{{\sigma }_x}$)+h($d_{{\sigma }_z}$)−1 calculated from the measured density matrix. Black squares denote the concurrence results, with the black solid line representing the theoretical prediction. The concurrence is always larger than 0, except for the state at x=0.5, which represents the separated state. Error bars represent the corresponding standard deviations.

We then further consider the case of storing photon B in a spin-echo based quantum memory. Figure 4a shows the real (R e) and imaginary (I m) parts of the density matrix, χ, characterizing the operation of the quantum memory (a detailed description of which is contained in the Methods). The operation of the optical delay is close to the identity, which serves as a high-quality quantum memory with a fidelity of about 98.3%. Figure 4b shows the experimental results obtained for the uncertainties as a function of the angle θ. We use two methods to estimate the uncertainty (see Methods). The red circles and blue squares represent the experimental results of H(R|B)+H(S|B) and H(R|R)+H(S|S), respectively. The uncertainty estimated by direct measurements of both A and B (H(R|R)+H(S|S)) is never less than the uncertainty estimated by the process of quantum state tomography (H(R|B)+H(S|B)), which provides an upper bound of the new uncertainty relation (1). The lower bound of the new uncertainty relation log₂(1/c(θ))+H(A|B) is less than zero when θ<38°, requiring that it be set to be zero. Error bars represent the standard deviations.

Figure 4: Experimental results for the density matrix χ of the spin-echo based quantum memory and the entropies as a function of the angle θ.

a, R e (χ)represents the real part of χ and I m (χ)represents the imaginary part of χ. b, The initial input state of AB system with B passing through the quantum memory was prepared as a quasi-maximal entangled state with the form close to , and the concurrence equals approximately 0.921, with a relative high entropy value for H(A|B) of about −0.692. The red circles and blue squares represent the experimental results of H(R|B)+H(S|B) and H(R|R)+H(S|S), respectively. The red and blue solid lines represent the corresponding theoretical predictions, which agree with the experimental results. Error bars represent the standard deviations (error bars of H(R|R)+H(S|S) are smaller than the corresponding symbols). The black dotted line represents the theoretical prediction of the lower bound of the uncertainty relation (1). When the lower bound is smaller than zero, it is set to zero (black solid line).

In conclusion, we have experimentally investigated the entropic uncertainty relation with the assistance of entanglement. Furthermore, this study verifies the application of the entropic uncertainty relation to witness the distillable entanglement assisted by one-way classical communication from A to B. Although the value of h($d_{{\sigma }_x}$)+h($d_{{\sigma }_z}$)−1 is dependent on the exact form of entangled states (see Supplementary Fig. S2), it can be obtained by a few separate measurements on each of the entangled particles¹, which shows its ease of accessibility. The method used to estimate uncertainties by directly performing measurements on both photons has practical application in verifying the security of quantum key distribution¹. Our results not only violate the previous classical uncertainty relation, but also confirm the new one proposed by Berta and colleagues¹. The verified entropic uncertainty principle implies that the uncertainty principle is not only observable-dependent, but is also observer-dependent², providing a particularly intriguing perspective. While preparing our manuscript for submission, we noted that another relevant experimental work was performed independently by Prevedel and colleagues²⁶.

Methods

Conditional entropies for ρ₁.

If the two observables are chosen to be R=σ_x and S=σ_z, the eigenvectors of R are and , and the eigenvectors of S are |0〉 and |1〉. As a result, the maximal complementarity (c) between R and S is 1/2, giving log₂(1/c)=1. For the initial input state ρ₁, the conditional von Neumann entropy on the left-hand side of the inequality (1) is calculated to be H(R|B)+H(S|B)=H(σ_x|B)+H(σ_z|B)=−2xlog₂x−2(1−x)log₂(1−x) and the right-hand side is calculated as log₂(1/c)+H(A|B)=−xlog₂x−(1−x)log₂(1−x). As a result, log₂(1/c)+H(A/B) gives the lower bound of H(σ_x|B)+H(σ_z|B) (0≤x≤1). At the points x=0 and x=1, that is, ρ₁ represents the maximally entangled state, for which the left-hand term and the right-hand term both equal 0.

Calculation of novel entanglement witness.

To obtain the values of h(d_R)+h(d_S)−1, the observable measurements (R=σ_x and S=σ_z) on both photons are directly performed by the polarization analysis measurement set-up (Fig. 1). The probabilities of obtaining the different outcomes of σ_x (σ_z) on A and B are calculated as $d_{{\sigma }_x}$=(N_{D J}+N_{J D})/(N_{D D}+N_{D J}+N_{J D}+N_{J J}) ($d_{{\sigma }_z}$=(N_{H V}+N_{V H})/(N_{H H}+N_{H V}+N_{V H}+N_{V V})), where N_{i j} represents the coincident counts when the photon state of A is projected onto |i〉 and B is projected onto |j〉 (|i〉,|j〉∈{|D〉,|J〉,|H〉,|V〉}).

Concurrence.

For a two-qubit state ρ, the concurrence²⁵ is given by

where , and the quantities λ_j are the eigenvalues in decreasing order of the matrix , with σ_y denoting the second Pauli matrix. The variable ρ* corresponds to the complex conjugate of ρ in the canonical basis {|00〉,|01〉,|10〉,|11〉}.

Quantum memory.

In our experiment, the quantum memory is constructed using two polarization maintaining (PM) fibres, each of 120 m length, and two half-wave plates, with the angles set at 45°, as shown in Fig. 1. Both PM fibres are set at the same preference basis {|H〉,|V〉}. Consider a photon with the polarization state α|H〉+β|V〉 (α and β are the two complex coefficients of the corresponding polarization states |H〉 and |V〉) passing through one of the fibres. As a result of the different indices of refraction for the horizontal and vertical polarizations in the PM fibre, different phases are imposed on the corresponding polarization states; which can be written as $\alpha {\text{e}}^{{\varphi }_H}|\text{H}〉\text{+}\beta {\text{e}}^{{\varphi }_V}|V〉$ 〉 for simplicity. A half-wave plate is then implemented by exchanging |H〉 and |V〉. After the photon passes the same second PM fibre, the state becomes ${\text{e}}^{i({\varphi }_H+{\varphi }_V)}$(α|V〉+β|H〉) and the coherence of the state is recovered. We then apply another half-wave plate to exchange |H〉 and |V〉, and the state is restored to the initial form. This process is similar to spin-echo phenomenon in nuclear magnetic resonance, with the photon being stored in the PM fibres for about 1.2 μs. Therefore, this system may serve as a spin-echo based quantum memory.

We then characterize the spin-echo based quantum memory using quantum process tomography²⁷. Its operator can be expressed on the basis of and written as:

The basis of we chose is {I,X,Y,Z}, where Irepresents the identity operation and X, Y and Z represent the three Pauli operators, respectively. The matrix χ completely and uniquely describes the process ɛ and can be reconstructed by experimental tomographic measurements. In the experiment, the physical matrix χ is estimated by the maximum-likelihood procedure²⁸, which is represented in Fig. 4a. It is close to the identity, and the fidelity of the experimental result is about 98.3%, which is calculated from with χ_ideal=I. As a result, the spin-echo based optical delay acts as a high-quality quantum memory.

Estimation of uncertainties with quantum memory.

In the experiment employing quantum memory, we change the complementarity of the two observables to be measured. The operator S is chosen to be σ_z, with the eigenvectors |H〉 and |V〉, whereas the other operator R is chosen to be in the X–Z plane with the eigenvectors cosθ|H〉+sinθ|V〉 and sinθ|H〉−cosθ|V〉. As a result, the complementarity of these observables becomes c(θ)=−log₂max[cosθ²,sinθ²]. We use two methods to estimate the uncertainty. The first is based on quantum state tomography, which is given by the conditional von Neumann entropy H(R|B)+H(S|B). The other quantity, directly estimated by the coincidence counts used for the same measurements on both A and B, is represented by H(R|R)+H(S|S). For example, , in which N represents the total coincidence counts and N₁=N_{H H}+N_{V H} (N₂=N_{H V}+N_{V V}) represents the counts when the state of photon B is projected onto |H〉 (|V〉) by tracing the photon A. As H(R|R)+H(S|S)≥H(R|B)+H(S|B), H(R|R)+H(S|S) provides an upper bound for the new uncertainty relation (1).

Error estimation.

In our experiment, the pump power is about 100 mW, and the total coincident counts are about 6,000 in 30 s. The statistical variation of each count is considered according to a Poisson distribution and the error bars are estimated from the standard deviations of the values calculated by the Monte Carlo method²⁹.