Main

Slip avalanches in slowly sheared granular materials, such as sand and powders, are important for many industrial, engineering, and geophysical processes. Understanding and predicting the dependence on packing fraction, shear rate, and frictional properties are the questions addressed here.

In contrast to traditional models based on continuum mechanics1 or on simulations of each individual grain, we use an analytical, discrete, coarse-grained approach. We analytically derive predictions for the statistical properties of slip avalanches at slow shear rates, where grain inertia is negligible (the ‘quasi-static’ regime). (We do not consider the regimes where grain inertia is non-negligible, such as granular gases2,3). Previous studies focused on jamming4,5, force chains3,5,6,7,8,9, stress drops during avalanches (refs 10, 11, 12; P. Yu, T. Shannon, B. Utter & P. R. Behringer, unpublished data and R. P. Behringer, private communication), and shear localization in shear bands1,2,13,14. Here, we consider a simple model for slip avalanche statistics.

We model the simplified system on a coarse-grained scale (larger than the grain diameter) with a lattice of sites that can either stick or slip under shear. The lattice is either two- or three-dimensional. It has linear extent L and N=Ld sites, where d is the dimension of the lattice. Nocc sites are occupied by grains and N−Nocc sites are empty (voids). The ‘grain number fraction’, v≡Nocc/N is proportional to the rescaled packing fraction Φ/Φmax, with v=1 for the densest possible packing Φ=Φmax. Initially all sites are stuck at random initial stresses. We apply a slow shear strain rate by moving one boundary of the lattice at a very slow parallel velocity V (see Fig. 1). This leads to a slow increase of shear stress at each lattice point. A site i slips in the shear direction when its local shear stress τi exceeds a random static ‘frictional’ failure stress τs,i (i=1,…,N). (The shape of the narrow distribution of the τs,i does not affect the behaviour on long length scales15.) A failing site slips during one time step until its stress is relaxed to a local ‘arrest stress’ τa,i<τs,i. It then resticks, with a weakened, dynamic failure threshold16 of τd,i≡τs,i−ɛ (τs,i−τa,i)>τa,i. Here ɛ≥0 is a ‘weakening parameter’ that quantifies the difference between effective static and dynamic ‘friction’ on meso-scales (larger than the contact level)14,17,18. Weakening is associated with dilation, the evolution of frictional resistance, and other effects. It could presumably be tuned by changing the shape and surface of the grains and the packing fraction. A slipping site can trigger other sites to slip in the next time step and so on. The slip avalanche stops when the stresses at all sites are below their current failure thresholds. All failure thresholds then reheal to their static values τs,i. The material continues to be slowly sheared until a new avalanche starts. (Shear rates faster than the rehealing rate may lead to shear band formation. Here we assume the shear band spans the entire modelled region12.)

Figure 1: Analytically computed dynamic ‘mean field phase diagram’.
figure 1

Left: Granular materials can respond like a solid or more like a fluid under slow shear, depending on the grain number fraction v multiplied by c=J/(J+KL)≈1, and the frictional weakening ɛ. The bold line is the phase boundary c v*(ɛ)=1/(1+ɛ) separating the solid phase from the fluid-like phase. At c v=1 and ɛ=0 is a critical point (see Table 1). Right: Sketch of the sheared model lattice with voids (that is, v<1,Φ<Φmax). The ‘linear system size L ’ is the length of the edges of the (square) granular region in the figure.

Full size image

To solve the model we make the following simplifying assumptions: (1) We study the ‘steady state’, when all memory of the initial conditions has decayed. (2) It is known that at high packing fractions granular materials have long force chains that often span the entire system3,5,6,7,8,9. Long force chains facilitate long range interactions. We approximate them by infinite-range mean field (MF) coupling J between the lattice sites (see Supplementary Information). Mean Field Theory (MFT) effectively averages out the spatial dependencies. (MFT also correctly describes slips in sheared plastic solids19,20,21.) (3) Concepts such as anisotropy in the contact distribution and/or the force-intensity distribution, as well as anisotropy and rotation of particles are neglected. (4) Rather than calculating the exact sequence of slips we compute statistical properties on long length scales, such as the probability distributions for large avalanche sizes, long avalanche durations and related measures, as a function of the key model parameters v and ɛ. (The dependence on the shear rate V is discussed in the Supplementary Information.)

The lattice occupation variable, oi,=1 if site i is occupied and oi,=0 if site i is vacant. ui(t) is the total amount of slip (the ‘displacement discontinuity’) at site i and time t. In MFT, ui(t) couples to the average cumulative slip, . The total shear stress τi(t) at site i and at time t is

The bulk acts like a soft spring (with constant KL∼1/L), coupling the lattice to the boundary15. A failing site i slips by an amount Δui=Δτioi/(J+KL). The associated local stress drop is Δτi≡ (τs,i−τa,i), or, for a weakened cell, Δτi≡ (τd,i−τa,i). The coupling J redistributes Δτi to the other sites k≠i, thereby increasing their stress by Δτk=oiok|Δτi|J/[(J+KL)N]. We call c≡J/(J+KL)≈1−O(1/L)≈1 (refs 15, 22). The total redistributed stress is then (see Supplementary Information)

It is smaller than the original stress drop |Δτi| by a factor v c=(Nocc/N)J/(J+KL)≤1. Equation (2) means that voids in granular materials effectively ‘dissipate’ a fraction 1−v c of the released stress. Consequently, on average, the avalanches are smaller when the grains are packed less densely.

For high number fractions (v c≈1,ɛ≈0,V →0) MFT predicts that the distribution D(s) of slip avalanche sizes decays for large s as D(s)∼s−κF(s/smax) (ref. 22). The MFT exponent κ=3/2, and the cutoff function F are expected to be the same for many different materials (‘universal’). F(s/smax)≈ constant for s≪smax and F(s/smax) decays exponentially for s≫smax. The cutoff smax scales with the number fraction v as smax (v c,ɛ=0,V →0)∼(1−v c)−2 (see Fig. 2).

Figure 2: Analytically predicted mean field slip avalanche size distribution D(s) for decreasing granular number fractions v.
figure 2

Here v1c=0.99 (black), v2c=0.95 (red), v3c=0.9 (green) and v4c=0.7 (blue), for ɛ=0, V →0, and c=1. Note that the power law D(s)∼s−3/2 extends to the largest sizes for the highest number fraction, that is, as v c→1. The power law agrees with experiments28, see Table 1. The maximum (‘cutoff’) avalanche size scales as smax∼(1−v c)−2. The distributions D(s) are normalized. The avalanche slip size s is in arbitrary units. (For ɛ>0,D(s) develops a bump22.)

Full size image

Similarly, the power spectrum (the absolute square of the Fourier transform) of the total slip rates scales in MFT as Pω(ω)∼ω−2P1(ω/ωmin) (refs 21, 22). Here P1(ω/ωmin)≈ constant for frequency ω>ωmin(v,ɛ,V) and low-frequency cutoff ωmin(v,ɛ=0,V →0)∼(1−v c) (see Fig. 3). Further predictions, such as the V - and ɛ -dependence of D(s) and Pω(ω), and possible experimental tests are discussed in the Supplementary Information.

Figure 3: Illustration of the mean field power spectra at different granular number fractions v.
figure 3

Here v1>v2>v3>v4 with ɛ→0 and V →0. Note that at high number fraction the power spectrum scales as P(ω)∼ω−2 (as seen in experiments10,11,12,28) for frequencies ω above a low-frequency cutoff ωmin. The low-frequency cutoff to the power law region scales as ωmin (v,ɛ=0)∼(1−v c), with c≈1. For decreasing number fractions an increasing range of low frequencies ω<ωmin scales as ω0=const (white noise), in agreement with simulations14,17,18.

Full size image

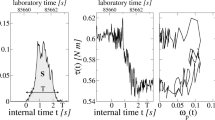
Much can be learned from the average temporal slip rate profile, 〈V (t,T)〉 (see Fig. 4). It is the total slip rate versus time t during an avalanche, averaged over all avalanches with same duration T. In MFT it is a parabola 〈V (t,T)〉∼t(T−t)/T (refs 23, 24, 25). Aharonov and Sparks fitted a sine function to their simulation results, but a parabola may fit equally well14,17,18. Many other scaling predictions can be computed from MFT (refs 15, 23, 24, 26, 27). Table 1 shows good agreement of the MFT results with experiments and simulations.

Figure 4: Rescaled average temporal slip rate profile, or temporal mean field avalanche ‘shape’.
figure 4

The profile is obtained from the average total slip rate 〈V (t,T)〉 during an avalanche versus time t (the ‘source time function’), averaged over all avalanches with the same duration T. This function is a prediction for avalanches in the power law scaling regime s<smax(v,ɛ,V) of D(s), for v c close to 1 and ɛ close to 0 and V →0. In MFT 〈V (t,T)〉∼A x(1−x) (refs 23, 24, 25, 26), where x≡t/T. A is a nonuniversal constant (A=4 in the figure), see ref. 26 and the Supplementary Information. A parabola was recently seen in experiments28.

Full size image
Table 1 Comparison of MFT results (power law exponents and scaling behaviour) with numerical simulations and experiments.
Full size table

In the solid-like regime (v>v*(ɛ) with v*(ɛ)≡1/(c(1+ɛ))), MFT predicts mode switching22: the material flip-flops between time periods with power law distributed avalanches, and periods with ‘quasi-periodically’ recurring macroscopically large events with only small precursors (‘stick-slip’). This behaviour is also seen in experiments28. The mean durations of these periods depend on v, ɛ and details of the system22. As ɛ→0 and v c→1 all the time is spent in the power law phase.

In the fluid-like regime (v<v*(ɛ)), MFT predicts only small avalanches without mode-switching22. This regime resembles the ‘fluid’ phase in experiments and simulations at low number fractions14,17,18. In the simulations, the power spectrum P(ω)∼ω0 (‘white noise’) in this phase. The analogous quantity in our model is the power spectrum of the time series of ΣmKL(V t−um(t)), which scales as P(ω)∼ω0 for v≪v*(ɛ), in agreement with simulations and experiments. In all parameter regimes the slip locations are randomly spread throughout the shear band, as seen in experiments12 and simulations14,17,18.

To conclude, an analytical MFT model is developed which yields a new phase diagram (Fig. 1) for the avalanche statistics of sheared granular materials. The tuning parameters are the grain number fraction v, the frictional weakening ɛ, and the shear rate V . Table 1 demonstrates agreement between results from MFT, experiments, and numerical simulations.

Mapping to other systems: remarkably, the universal aspects of avalanches in sheared granular materials at high v (this paper), dislocation slips in solids19,20,21, and earthquakes15,16,22,26,27,29 can all be modelled by variants of the same MFT (refs 15, 16, 22, 27), and are thus expected to have the same critical exponents. (The variants describe the undiluted case, that is, v=1.) A similar connection between avalanches in granular materials and magnetic domain walls has been pointed out10,11. Connections between granular avalanches and earthquakes have been discussed6,16. Observations and experiments on these systems yield critical exponents with overlapping error bars. Further studies of the spatial correlations in finite dimensions will aid in the challenging quest for a simple unifying theory underlying the dynamics of these different systems.