Abstract
Electron acceleration by laser-driven plasma waves1,2 is capableof producing ultra-relativistic, quasi-monoenergetic electron bunches3,4,5 with orders of magnitude higher accelerating gradients and much shorter electron pulses than state-of-the-art radio-frequency accelerators. Recent developments have shown peak energies reaching into the GeV range6 and improved stability and control over the energy spectrum and charge7. Future applications, such as the development of laboratory X-ray sources with unprecedented peak brilliance8,9 or ultrafast time-resolved measurements10 critically rely on a temporal characterization of the acceleration process and the electron bunch. Here, we report the first real-time observation of the accelerated electron pulse and the accelerating plasma wave. Our time-resolved study allows a single-shot measurement of the 5.8−2.1+1.9 fs electron bunch full-width at half-maximum (2.5−0.9+0.8 fs root mean square) as well as the plasma wave with a density-dependent period of 12–22 fs and reveals the evolution of the bunch, its position in the surrounding plasma wave and the wake dynamics. The results afford promise for brilliant, sub-ångström-wavelength ultrafast electron and photon sources for diffraction imaging with atomic resolution in space and time11.
Similar content being viewed by others
Main
The recent development in laser wakefield acceleration (LWFA) is made feasible by transverse breaking of the plasma wave12, which results in self-injection and trapping of electrons in the accelerating structure2,13,14. Whereas beam parameters such as the energy spectrum, accelerated charge, beam divergence and pointing are now being measured routinely with methods adopted from conventional accelerator technology, the duration of electron bunches arising from LWFA has so far defied accurate determination. Bunch duration measurements up to now have relied on techniques using THz radiation emitted by the electrons, yielding upper limits for the electron pulse length corresponding to the temporal resolution of ≥30 fs (refs 15, 16, 17, 18). The plasma wave has been observed so far in single-shot, yet time-integrating schemes19,20. Thus, the measurements were incapable of providing insight into the relevant plasma wave dynamics and of timing the accelerated electron bunch with respect to the plasma wave.
In this work we present snapshots of the magnetic field generated by the accelerated electron bunch and—simultaneously—of the plasma wave by the combination of two techniques: time-resolved polarimetry21,22 and plasma shadowgraphy23. The novelty in our experimental investigation is the few-cycle duration of our laser pulses, which is even shorter than half of the plasma period. This, in combination with a high spatial resolution, allows us to measure for the first time the position and temporal structure of the electron bunch duration with an unprecedented resolution and observe at the same time the plasma wave dynamics during injection and acceleration of electrons in the wake of the laser pulse.
Sub-10-fs polarimetry is based on the probe pulse undergoing polarization rotation due to the Faraday effect caused by the component of the magnetic field parallel to the k-vector of the probe (see inset in Fig. 1). The location, duration and charge of the electron bunch can be inferred from the measurement of the rotation angle φrot in the (y,z) plane (see Fig. 1) because of the uniquely short probe pulse used. Simultaneously, sub-10-fs shadowgraphy provides—by means of density-dependent deflection of the probe beam—insight into the structure of the plasma wave accelerating the electrons. The combination of these techniques results in freeze-frame snapshots of the accelerating laser-driven plasma wave and the electron bunch ‘surfing’ this wave and permits the direct determination of the duration of electron bunches from LWFA.
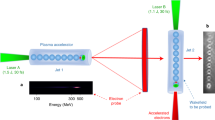
Electrons are accelerated by the drive laser beam (red arrow) out of a supersonic gas jet with a flattop density profile from a de Laval nozzle with 300 μm exit diameter (blue). The probe beam (black arrows) propagates perpendicularly to the main beam through the plasma. In the vicinity of the electron bunch the polarization is rotated by φrot as a result of the Faraday effect (inset, see equation (1)). The interaction region with the plasma wave is imaged to two CCD cameras (see Methods). In front of the cameras are two Glan-laser polarizers with high extinction ratios, which are rotated (blue arrows) away from extinction of the probe beam in opposite directions by ±7°. The shadowgrams are recorded simultaneously with both cameras.
To validate the intended methodology we have simulated LWFA driven by sub-10-fs multi-terawatt laser pulses with a three-dimensional (3D) particle-in-cell (PIC) code (ILLUMINATION; ref. 24) and calculated the emerging magnetic fields (see Methods). Figure 2a plots the simulated electron density distribution inside the plasma. The trapped electron bunch at the rear side of the ‘bubble’ is clearly discernible and coincides with the increase of the azimuthal magnetic field (peak field strength: 3.8 kT) around the bunch in Fig. 2b. Some electrons are not in the plotted plane because of transverse oscillations, leading to the apparent structure of the bunch in the density plot. The lineout in Fig. 2c shows that both the electron density and the magnetic field have the same duration of 5.5 fs full-width at half-maximum (FWHM).
a, Electron density. The remaining density in the first oscillation is ∼4×1018 cm−3. b, Azimuthal magnetic field. c, Lineout of the electron density map (black solid line) and the magnetic field map (red dashed line). d, Simulation of the polarization rotation angle distribution (image smoothed with Gaussian profile with 2 μm FWHM to simulate the experimental imaging resolution). e, Refraction of the probe beam (black rays) at the high density peaks of the plasma wave (red bars) at three instances in time. The probe beam is refracted already in the first half (transversely) of the plasma wave leading to a modulated intensity of the probe beam in the imaged plane (dashed line). f, Imaging this plane with a high resolution produces an intensity modulation on the camera (calculated with finite pulse duration and spatial resolution, red line) as a signature of the plasma wave (lineout from PIC simulations, black line).
The rotation of the probe beam polarization is simulated by tracking a probe pulse through the 3D field maps from the simulation without taking refraction of the probe beam inside the plasma into account (Fig. 2d). Limited imaging resolution is taken into account by convolving the simulated signal with a Gaussian spatial distribution having a FWHM of Δres=2.0 μm. The longitudinal extension of the regions with positive and negative rotation angle is 8 fs (FWHM). Further magnetic fields inside the bubble are generated by the displacement current, that is the temporally-varying longitudinal electric field. However, these fields are by a factor of ∼7 smaller than the field caused by the moving electrons and have a negligible effect on the longitudinal extension of the region with rotated polarization.
The rays of the probe beam are deflected as they traverse the plasma wave, depending on the electron density gradient, as illustrated in Fig. 2e. This leads to an intensity modulation of the probe beam in the plane at the centre of the plasma wave with the same periodicity. Imaging this plane using a camera with a high resolution and thus small depth of focus in turn shows the modulation as a shadowgram of the plasma wave on the camera. The modulation is not averaged out, because the probe pulse duration is shorter than half the plasma period and the depth of focus is small compared with the transverse size of the plasma wave. The modulation depth is proportional to the amplitude of the nonlinear plasma wave as calculated by ray tracing (Fig. 2f). Although, as Fig. 2f indicates, the measured oscillations are smoothed owing to limited resolution and do not reflect the strong nonlinearity of the real plasma wave, they still reflect its original period and position.
In the current study, the electron accelerator was driven by 8.5 fs (FWHM) laser pulses with an energy of 65 mJ on the target delivered by Light Wave Synthesizer-20 (LWS-20; ref. 25) focused onto a supersonic helium gas jet (see Methods), where electron bunches with a quasi-monoenergetic spectrum of Epeak=(19.2±6.7) MeV were produced. A 2-mJ probe pulse with the same duration τprobe was split from the beam through a hole in one of the plane mirrors before focusing and directed onto the gas jet perpendicularly to the main beam (Fig. 1).
The trapped relativistic electron bunch generates an azimuthal magnetic field localized around the electron bunch (Fig. 2b,c), which rotates the probe beam polarization as a result of the Faraday effect by the angle

where Bφ is the azimuthal magnetic field surrounding the electrons, e,me,c and nc the electron charge, electron mass, vacuum speed of light and critical density (here: nc=1.76×1021 cm−3) and ds a path element along the path l of the probe through the plasma. The rays of the probe beam passing the electron bunch above or below the laser axis are rotated in opposite directions. For a sensitive, low-background measurement of φrot, this region was also imaged onto two CCD cameras by using a non-polarizing beam splitter behind the imaging lenses22 (Fig. 1). Polarizers in front of the CCDs were rotated away from extinction of the original probe beam polarization in opposite directions by θpol,i=±(7.0±0.3)°, slightly greater than the expected rotation angles. Thus, the intensity in the images is modulated and regions with positive polarization rotation seem brighter on one camera than on the other. The measured intensity Ipol,i(y,z) on the two cameras (i=1,2) is given by

where I0(y,z) is the initial probe beam intensity, Ti the transmission through/reflection off the beam-splitter, and βi=1−1/ER,i, with ER,i being the polarization contrast of the beam in the corresponding arm. The rotation angle φrot can be deduced by inversion of the intensity ratio of the two images Ipol,1(y,z)/Ipol,2(y,z) (see Methods). The experimentally obtained polarization rotation is plotted in Fig. 3a, regions of positive and negative angle stand out from the background.
a, Polarization rotation angle of the probe beam due to the Faraday effect. Insets: Transverse and longitudinal lineout of the rotation angle. b, Combined rotation angle with background subtracted raw image showing the plasma wave and the rotated polarization (from the same shot as in a) at an electron density after fully ionizing the He gas of 3.2×1019 cm−3. c, Plasma wavelength/period versus electron density. Error bars are one standard deviation combined with scaling uncertainty. Each point is an average of 4–7 shots. The red line shows the theoretical non-relativistic plasma period according to equation (3).
A raw image of camera 1 (see Fig. 1) combined with the polarization rotation signal is plotted in Fig. 3b. The plasma wave trailing the laser pulse and the electron bunch—visualized by shadowgraphy (Fig. 2f)—is visible to the left of the region with rotated polarization. From the large number of plasma oscillations (typically 10–20), we learn that the plasma wave does not decay completely after the first wake. This indicates that the wake is not heavily loaded26, as this would lead to rapid destruction of the subsequent plasma oscillations. To obtain firm evidence for the origin of the observed oscillations, we measured their period as a function of electron density while all other experimental parameters were kept constant (Fig. 3c). The period of the plasma wave—in the non-relativistic limit—is given by

where ɛ0 is the vacuum permittivity and ne the electron density. The good agreement of the time-resolved plasma oscillation period with equation (3) corroborates that the oscillations originate from the plasma wave and reveal that the period is not significantly elongated by relativistic effects under our experimental conditions27. This observation is in agreement with the results of our simulations, which predict that the plasma period depends only weakly on the laser intensity (at least) up to Ipeak=1.0×1019 W cm−2(a0=2.1). Although the unparalleled spatio-temporal resolution of our probing makes plasma dynamics and accelerated electron bunching directly observable for the first time, this resolution still has to be further improved to unravel details of these dynamics such as non-sinusoidal plasma oscillations.
As shown in Fig. 2c, the electron pulse duration can be directly inferred from the polarization rotation signal. Averaging over 85 shots, the rotation signal seems to have a longitudinal extent of Δrot=(3.8±0.2) μm (FWHM). The deconvolution (see Methods) of the longitudinal extent yields a mean FWHM electron bunch duration of τbunch=5.8−2.1+1.9 fs (2.5−0.9+0.8 fs root mean square), which is in excellent agreement with the simulated value. The simulation shows that contributions to the region of rotated polarization from the electrons constituting the plasma wave at the bubble vertex cannot be neglected. Consequently, the actual bunch duration is expected to be even shorter than the result of our above analysis.
A change in time delay between the main laser pulse and probe beam allows snapshots at various stages of the acceleration and thus tracking the evolution of the electron bunch and the plasma wave (see Fig. 4c–i and Supplementary Movie). The first polarization rotation signals are detected after a propagation distance of the laser pulse of 190 μm in the gas jet, see Fig. 4a. The mean duration of the polarization rotation signal and the deconvolved electron bunch duration are also shown in Fig. 4a for each delay step, that is each position inside of the plasma. It can be seen that τbunch is constant within the error bars, showing an upper limit of 7–8 fs (FWHM). Also plotted is the peak polarization rotation angle, which is proportional to the beam current. The nearly constant bunch duration and peak rotation angle imply that the total injected charge remains constant in the last third of the gas jet. The vanishing of φrot for z<190 μm and its reaching a maximum at about z=220 μm, in combination with a nearly constant τbunch, indicates that injection is confined to a propagation length of about 30 μm close to z=200 μm downstream from the entrance of the plasma channel28. Over approximately the same longitudinal range, the accelerating plasma wave exhibits a decrease in total length as well as in its amplitude that is proportional to the modulation depth of the probe intensity variations (Fig. 4b). This reduction in the plasma wave amplitude is caused by the injected and accelerated electrons that are not located at the regions of high electron density in the plasma wave but between high and low density regions. Thus, these electrons do not contribute to the longitudinal electric field but in contrast damp it. Both observations are consistent and indicate that our approach provides real-time access to the electron injection and trapping process of a laser-driven plasma accelerator. As no polarization rotation signal is observed before z=190 μm, where the plasma wave amplitude is larger, the contribution to the magnetic field of the displacement current is indeed negligible for the measurement, as also indicated by the simulation.
The 300 μm He gas jet is centred around z=150 μm. a, Evolution of the deconvolved FWHM electron pulse duration (red stars), the original duration of the polarization rotation (grey squares), and the peak polarization rotation angle (blue diamonds) during the propagation through the plasma. Each point is an average of 4–22 measurements, error bars are 1 s.d. b, Simultaneous evolution of the number of identifiable plasma oscillations in the raw images, for example Fig. 3b, (green circles) and the intensity modulation depth (brown triangles) in the shadowgraphy images. Each point is an average of five measurements, error bars are one standard deviation c–i, Representative lineouts along the laser propagation axis (slightly tilted to the z axis) of the intensity modulation due to probe beam refraction (see Fig. 2e) at the plasma wave (black line) and position and duration of the deconvolved electron pulse duration (red line) for different delay steps. The background plasma density is 3.2×1019 cm−3. The nonlinearity of the plasma wave cannot be seen here because of the spatial and temporal resolution. The plasma wave is detected in all shots at a particular delay, however the modulation visibility and apparent length fluctuate from shot to shot. Individual shots with both the plasma wave and the electron bunch most clearly visible were selected for these lineouts. The apparent dependence of electron bunch duration on position is not representative. c, The plasma wave at z=183 μm, where no polarization rotation due to an injected electron bunch is detected.
Figure 4c–i shows, for different delays, lineouts of the intensity modulation due to the plasma wave together with the position and longitudinal extension of the accelerated electron bunch, with the latter inferred from the time-resolved polarimetry data under the assumption of a Gaussian temporal shape of the bunch. The intensity modulation is visible only behind the Faraday rotation signal, except for one maximum caused by the electrons that are being pushed forward by the laser, which can appear in front of the electrons in some shots (for example Fig. 4g). This reveals that the accelerated main electron bunch is trapped inside the first plasma wave oscillation, in agreement with our simulation (Fig. 2a) as well as earlier experiments29. A small number of electrons can be found in the second period in the simulation, however the order-of-magnitude weaker magnetic field around those electrons is not expected to be detectable with our current apparatus.
Our new technique, giving insight into the acceleration process with unprecedented spatial and temporal resolution, will help to understand the details of self-injection of electrons into laser wakefields and is likely to influence numerical work and future experiments aiming at a coherent description of the underlying physics. Polarization rotation caused by the Faraday effect presents the first direct observation of the electron bunch duration and could also be used for electron characterization in linear accelerators that generate ultrashort bunches.
Methods
Particle-in-cell simulations. The simulation was performed with the code ILLUMINATION24 using parameters matching the experimental conditions. An 8.0 fs pulse (FWHM) is focused to a spot size of 7.2 μm FWHM, reaching a peak intensity of Ipeak=5.8×1018 W cm−2. The focus is located in the centre of a 300 μm long flat top density profile with ne=3.5×1019 cm−3. The complete box has an extension of 48.5 μm longitudinally and 45.2 μm transversally.
Laser-plasma accelerator. The experiments were performed with Light Wave Synthesizer-20 (LWS-20) at Max-Planck-Institut für Quantenoptik (MPQ) in Garching, Germany, an optical parametric chirped pulse amplification system25 producing pulses as short as 7.7 fs with peak powers up to 16 TW at a carrier wavelength of 800 nm. In the current study, LWS-20 delivered 8.5 fs (FWHM) pulses with an energy of 65 mJ on the target, taking losses due to adaptive optics and the beamline into account. The few-cycle laser pulses were focused onto the gas target with a f/6 off-axis parabolic mirror to a spot size of 7.2 μm FWHM and a peak intensity of Ipeak=6×1018 W cm−2 (a0=1.67) to accelerate electron bunches by means of self-injection in the bubble/blow-out regime.
A supersonic helium jet from a de Laval nozzle with 300 μm exit diameter producing a flattop density profile was used as gas target. The plasma density after fully ionizing the He gas was 3.2×1019 cm−3. The electron density ne was inferred from the gas density determined with a Mach–Zehnder interferometer and assuming complete ionization.
The accelerated electron bunches exhibited a quasi-monoenergetic spectrum of Epeak=(19.2±6.7) MeV, an energy spread of ΔE=(2.3±1.9) MeV (FWHM), a divergence of (10.9±3.5) mrad (FWHM) and carried a charge of Q=(2.3±1.8) pC, in a set-up similar to that described in ref. 30. These statistics were calculated with all 2,300 shots from one electron run; error bars are one standard deviation (s.d.).
Imaging and rotation angle evaluation. The interaction region was imaged onto the two CCD cameras using a combination of a long-working distance plan-apochromatic microscope objective with f=20 mm (Mitutoyo) and an achromatic lens with f=250 mm (Thorlabs; see Fig. 1). The achieved resolution was measured to be Δres=(2.0±0.3) μm by looking at the smallest resolvable structures from the ionized channel. Two Glan-laser polarizers with high extinction ratios were used. The polarization contrast for equation (2), which is dependent on the initial laser polarization, the beamsplitter properties and the polarizer extinction ratio, was measured to be β1=0.973±0.004 and β2=0.961±0.001. For our experimental parameters, the function Ipol,1/Ipol,2 is monotonic over a range of more than φrot=±11°, which is several degrees larger than the measured rotation angles. Thus, unambiguous numerical inversion to obtain φrot from the measured intensity ratio Ipol,1/Ipol,2 is possible.
The shot-to-shot timing jitter between pump and probe was estimated to be ±11 fs from the longitudinal jitter of the Faraday rotation signal at a fixed delay. However, this does not affect the relative timing accuracy of polarimetry and shadowgraphy of ∼4–5 fs (one quarter of the plasma wavelength), because they were both acquired simultaneously with the same probe beam.
Deconvolution of the electron bunch duration. The measured temporal length of the polarization rotation τrot=Δrot/c is a convolution of the electron bunch duration τbunch, the probe pulse duration τprobe=(8.5±0.5) fs, the transverse size of the azimuthal magnetic field (that is the transit time of the probe beam through the electron bunch) τtransv=Δtransv/c=3.3 fs and the imaging resolution τres=Δres/c=6.7 fs, which add quadratically. The value of τtransv is estimated from the PIC simulation and contributes only marginally to the measured duration of the magnetic field. The non-symmetric error of the electron pulse duration was calculated statistically using distribution functions for the four main parameters (τrot,τprobe,τtransv.,τres). The properties of these distributions were determined from the measurement. Calculating the deconvolution for each data set gives the statistical distribution, and thus the mean and the standard error, of the electron bunch duration.
PIC and particle tracking/space charge simulations indicate that the electron bunch duration after the gas jet is mainly affected by the energy spread. The elongation is negligible in a distance of 10 mm from the gas jet for the reported energy spread.
Change history
21 March 2011
In the version of this Letter originally published, the description of panels c–i in the caption for Fig. 4 was incomplete. This error has now been corrected in all versions of the Letter.
References
Tajima, T. & Dawson, J. M. Laser electron accelerator. Phys. Rev. Lett. 43, 267–270 (1979).
Pukhov, A. & Meyer-ter-Vehn, J. Laser wake field acceleration: The highly non-linear broken-wave regime. Appl. Phys. B 74, 355–361 (2002).
Mangles, S. P. D. et al. Monoenergetic beams of relativistic electrons from intense laser-plasma interactions. Nature 431, 535–538 (2004).
Geddes, C. G. R. et al. High-quality electron beams from a laser wakefield accelerator using plasma-channel guiding. Nature 431, 538–541 (2004).
Faure, J. et al. A laser-plasma accelerator producing monoenergetic electron beams. Nature 431, 541–544 (2004).
Leemans, W. P. et al. GeV electron beams from a centimetre-scale accelerator. Nature Phys. 2, 696–699 (2006).
Faure, J. et al. Controlled injection and acceleration of electrons in plasma wakefields by colliding laser pulses. Nature 444, 737–739 (2006).
Catravas, P., Esarey, E. & Leemans, W. P. Femtosecond X-rays from Thomson scattering using laser wakefield accelerators. Meas. Sci. Technol. 12, 1828–1834 (2001).
Fuchs, M. et al. Laser-driven soft-X-ray undulator source. Nature Phys. 5, 826–829 (2009).
Ihee, H. et al. Direct imaging of transient molecular structures with ultrafast diffraction. Science 291, 458–462 (2001).
Ivanov, M. & Krausz, F. Attosecond physics. Rev. Mod. Phys. 81, 163–234 (2009).
Bulanov, S. V., Pegoraro, F., Pukhov, A. M. & Sakharov, A. S. Transverse-wake wave breaking. Phys. Rev. Lett. 78, 4205–4208 (1997).
Lu, W., Huang, C., Zhou, M., Mori, W. B. & Katsouleas, T. Nonlinear theory for relativistic plasma wakefields in the blowout regime. Phys. Rev. Lett. 96, 165002 (2006).
Thomas, A. G. R. et al. Measurements of wave-breaking radiation from a laser-wakefield accelerator. Phys. Rev. Lett. 98, 054802 (2007).
Van Tilborg, J. et al. Temporal characterization of femtosecond laser-plasma-accelerated electron bunches using terahertz radiation. Phys. Rev. Lett. 96, 014801 (2006).
Ohkubo, T. et al. Temporal characteristics of monoenergetic electron beams generated by the laser wakefield acceleration. Phys. Rev. Spec. Top. Accel. Beams 10, 031301 (2007).
Van Tilborg, J., Tóth, Cs., Matlis, N. H., Plateau, G. R. & Leemans, W. P. Single-shot measurement of the spectral envelope of broad-bandwidth terahertz pulses from femtosecond electron bunches. Opt. Lett. 33, 1186–1188 (2008).
Debus, A. D. et al. Electron bunch length measurements from laser-accelerated electrons using single-shot THz time-domain interferometry. Phys. Rev. Lett. 104, 084802 (2010).
Matlis, N. H. et al. Snapshots of laser wakefields. Nature Phys. 2, 749–753 (2006).
Dong, P. et al. Formation of optical bullets in laser-driven plasma bubble accelerators. Phys. Rev. Lett. 104, 134801 (2010).
Stamper, J. A. & Ripin, B. H. Faraday-rotation measurements of megagauss magnetic fields in laser-produced plasmas. Phys. Rev. Lett. 34, 138–141 (1975).
Kaluza, M. C. et al. Measurement of magnetic-field structures in a laser-wakefield accelerator. Phys. Rev. Lett. 105, 115002 (2010).
Settles, G. S. Schlieren and Shadowgraph Techniques (Springer, 2001).
Geissler, M., Schreiber, J. & Meyer-ter-Vehn, J. Bubble acceleration of electrons with few-cycle laser pulses. New J. Phys. 8, 186 (2006).
Herrmann, D. et al. Generation of sub-three-cycle, 16 TW light pulses by using noncollinear optical parametric chirped-pulse amplification. Opt. Lett. 34, 2459–2461 (2009).
Rechatin, C. et al. Observation of beam loading in a laser-plasma accelerator. Phys. Rev. Lett. 103, 194804 (2009).
Matsuoka, T. et al. Stimulated Raman side scattering in laser wakefield acceleration. Phys. Rev. Lett. 105, 034801 (2010).
Hsieh, C-T. et al. Tomography of injection and acceleration of monoenergetic electrons in a laser-wakefield accelerator. Phys. Rev. Lett. 96, 095001 (2006).
Mangles, S. P. D. et al. Laser-wakefield acceleration of monoenergetic electron beams in the first plasma-wave period. Phys. Rev. Lett. 96, 215001 (2006).
Schmid, K. et al. Few-cycle laser-driven electron acceleration. Phys. Rev. Lett. 102, 124801 (2009).
Acknowledgements
We thank M. Geissler for providing us with the ILLUMINATION code to perform the PIC simulations. This work is supported by DFG-Project Transregio TR18, by the Association EURATOM, Max-Planck-Institut für Plasmaphysik, by the Munich Centre for Advanced Photonics (MAP), by Laserlab-Europe/Labtech FP7 contract number 228334 and by the German Ministry of Education and Research (BMBF) under contract 03ZIK052. C.M.S.S. acknowledges the support of the Alexander von Humboldt Foundation. J.M.M. acknowledges the support of the Alexander von Humboldt Foundation and the Russian Foundation for Basic Research (RFBR), grant numbers 08-02-01245-a and 08-02-01137-a.
Author information
Authors and Affiliations
Contributions
A.B., M.N., K.S., C.M.S.S., A.S., M.C.K. and L.V. designed and carried out the experiments. A.B. and M.N. did the main data analysis. A.B. and J.M.M. performed the simulations. F.K., M.C.K. and L.V. provided overall guidance to the project. All authors discussed the results and contributed to the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Information (PDF 169 kb)
Supplementary Information
Supplementary Information (MOV 3386 kb)
Rights and permissions
About this article
Cite this article
Buck, A., Nicolai, M., Schmid, K. et al. Real-time observation of laser-driven electron acceleration. Nature Phys 7, 543–548 (2011). https://doi.org/10.1038/nphys1942
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys1942
This article is cited by
-
Self action effects of q-Gaussian laser beam in preformed parabolic plasma channels: effect of nonlinear absorption
Journal of Optics (2024)
-
Unveiling the inner structure of electron pulses generated from a laser-wakefield accelerator
Light: Science & Applications (2023)
-
A beamline to control longitudinal phase space whilst transporting laser wakefield accelerated electrons to an undulator
Scientific Reports (2023)
-
Femtosecond electron microscopy of relativistic electron bunches
Light: Science & Applications (2023)
-
Direct observation of relativistic broken plasma waves
Nature Physics (2022)