Abstract
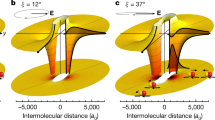
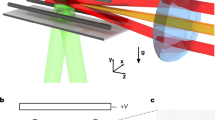
Molecular collisions in the quantum regime represent a new opportunity to explore chemical reactions. Recently, atom-exchangereactions were observed in a trapped ultracold gas of KRb molecules. In an external electric field, these polar molecules can easily be oriented and the exothermic and barrierless bimolecular reactions, KRb+KRb→K2+Rb2, occur at a rate that rises steeply with increasing dipole moment. Here we demonstrate the suppression of the bimolecular chemical reaction rate by nearly two orders of magnitude when we use an optical lattice trap to confine the fermionic polar molecules in a quasi-two-dimensional, pancake-like geometry, with the dipoles oriented along the tight confinement direction. With the combination of sufficiently tight confinement and Fermi statistics of the molecules, two polar molecules can approach each other only in a ‘side-by-side’ collision under repulsive dipole–dipole interactions. The suppression of chemical reactions is a prerequisite for the realization of new molecule-based quantum systems.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Zare, R. N. Laser control of chemical reactions. Science 279, 1875–1879 (1998).
Aldegunde, J. et al. How reactants polarization can be used to change and unravel chemical reactivity. J. Phys. Chem. A 109, 6200–6217 (2005).
Gijsbertsen, A., Linnartz, H., Taatjes, C. A. & Stolte, S. Quantum interference as the source of steric asymmetry and parity propensity rules in NO-rare gas inelastic scattering. J. Am. Chem. Soc. 128, 8777–8789 (2006).
Ospelkaus, S. et al. Quantum-state controlled chemical reactions of ultracold KRb molecules. Science 327, 853–857 (2010).
Ni, K-K. et al. Dipolar collisions of polar molecules in the quantum regime. Nature 464, 1324–1328 (2010).
Büchler, H. P. et al. Strongly correlated 2D quantum phases with cold polar molecules: Controlling the shape of the interaction potential. Phys. Rev. Lett. 98, 060404 (2007).
Micheli, A. et al. Cold polar molecules in two-dimensional traps: Tailoring interactions with external fields for novel quantum phases. Phys. Rev. A 76, 043604 (2007).
Pupillo, G., Micheli, A., Büchler, H. P. & Zoller, P. in Cold Molecules: Theory, Experiment, Applications (eds Krems, R. V., Friedrich, B. & Stwalley, W. C.) 421–469 (CRC, 2009).
Baranov, M. Theoretical progress in many-body physics with ultracold dipolar gases. Phys. Rep. 464, 71–111 (2008).
Lahaye, T., Menotti, C., Santos, L., Lewenstein, M. & Pfau, T. The physics of dipolar bosonic quantum gases. Rep. Prog. Phys. 72, 126401 (2009).
Wang, D. W., Lukin, M. D. & Demler, E. Quantum fluids of self-assembled chains of polar molecules. Phys. Rev. Lett. 97, 180413 (2006).
Klawunn, M., Duhme, J. & Santos, L. Bose–Fermi mixtures of self-assembled filaments of fermionic polar molecules. Phys. Rev. A 81, 013604 (2010).
Capogrosso-Sansone, B. et al. Quantum phases of cold polar molecules in 2D optical lattices. Phys. Rev. Lett. 104, 125301 (2010).
Sawyer, B. C. et al. Cold heteromolecular dipolar collisions. Preprint at http://arxiv.org/abs/1008.5127 (2010).
Krems, R. V. Molecules near absolute zero and external field control of atomic and molecular dynamics. Int. Rev. Phys. Chem. 24, 99–118 (2005).
Carr, L. D. et al. Cold and ultracold molecules: Science, technology and applications. New J. Phys. 11, 055049 (2009).
Stuhler, J. et al. Observation of dipole–dipole interaction in a degenerate quantum gas. Phys. Rev. Lett. 95, 150406 (2005).
Ticknor, C. Quasi-two-dimensional dipolar scattering. Phys. Rev. A 81, 042708 (2010).
Quéméner, G. & Bohn, J. L. Electric field suppression of ultracold confined chemical reactions. Phys. Rev. A 81, 060701 (2010).
Micheli, A. et al. Universal rates for reactive ultracold polar molecules in reduced dimensions. Phys. Rev. Lett. 105, 073202 (2010).
DeMarco, B., Bohn, J. L., Burke, J. P. Jr, Holland, M. & Jin, D. S. Measurement of p-wave threshold law using evaporatively cooled fermionic atoms. Phys. Rev. Lett. 82, 4208–4211 (1999).
Ospelkaus, S. et al. Controlling the hyperfine state of rovibronic ground state polar molecules. Phys. Rev. Lett. 104, 030402 (2010).
Ni, K-K. et al. A high-phase-space-density gas of polar molecules. Science 322, 231–235 (2008).
Kastberg, A., Phillips, W. D., Rolston, S. L., Spreeuw, R. J. C. & Jessen, P. S. Adiabatic cooling of cesium to 700 nK in an optical lattice. Phys. Rev. Lett. 74, 1542–1545 (1995).
Greiner, M., Bloch, I., Mandel, O., Hänsch, T. W. & Esslinger, T. Exploring phase coherence in a 2D lattice of Bose–Einstein condensates. Phys. Rev. Lett. 87, 160405 (2001).
Quéméner, G. & Bohn, J. L. Dynamics of ultracold molecules in confined geometry and electric field. Phys. Rev. A 83, 012705 (2010).
Idziaszek, Z. & Julienne, P. S. Universal rate constants for reactive collisions of ultracold molecules. Phys. Rev. Lett. 104, 113202 (2010).
Petrov, D. S. & Shlyapnikov, G. V. Interatomic collisions in a tightly confined Bose gas. Phys. Rev. A 64, 012706 (2001).
Li, Z. & Krems, R. V. Inelastic collisions in an ultracold quasi-two-dimensional gas. Phys. Rev. A 79, 050701(R) (2009).
Quéméner, G. & Bohn, J. L. Strong dependence of ultracold chemical rates on electric dipole moments. Phys. Rev. A 81, 022702 (2010).
Zuchowski, P. S. & Hutson, J. M. Reactions of ultracold alkali metal dimers. Phys. Rev. A 81, 060703 (2010).
Byrd, J. N., Montgomery, J. A. Jr & Côté, R. Structure and thermochemistry of K2Rb, KRb2 and K2Rb2 . Phys. Rev. A 82, 010502 (2010).
Meyer, E. R. & Bohn, J. L. Product-state control of bi-alkali-metal chemical reactions. Phys. Rev. A 82, 042707 (2010).
Ospelkaus, S. et al. Ultracold polar molecules near quantum degeneracy. Faraday Discuss. 142, 351–359 (2009).
Acknowledgements
We thank P. Julienne, P. Zoller, G. Pupillo and A. Micheli for stimulating discussions and S. Moses for technical contributions. We gratefully acknowledge financial support for this work from NIST, NSF, AFOSR-MURI, DOE and DARPA.
Author information
Authors and Affiliations
Contributions
The experimental work and data analysis were carried out by M.H.G.d.M., A.C., B.N., D.W., S.O., J.Y. and D.S.J. Theoretical calculations of the inelastic loss rates in the 2D trap were done by G.Q. and J.L.B.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
About this article
Cite this article
de Miranda, M., Chotia, A., Neyenhuis, B. et al. Controlling the quantum stereodynamics of ultracold bimolecular reactions. Nature Phys 7, 502–507 (2011). https://doi.org/10.1038/nphys1939
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys1939
This article is cited by
-
Raman sideband cooling of molecules in an optical tweezer array
Nature Physics (2024)
-
Universal machine learning for the response of atomistic systems to external fields
Nature Communications (2023)
-
Transition from an atomic to a molecular Bose–Einstein condensate
Nature (2021)
-
Tuning of dipolar interactions and evaporative cooling in a three-dimensional molecular quantum gas
Nature Physics (2021)
-
Towards chemistry at absolute zero
Nature Reviews Chemistry (2021)