Abstract
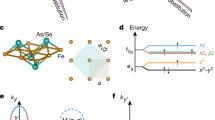
The discovery of superconductivity in LaFeAsO introduced ferropnictides as a new class of superconducting compounds with critical temperatures second only to those of the cuprates. Although the presence of iron makes the ferropnictides radically different from the cuprates, antiferromagnetism in the parent compounds suggests that superconductivity and magnetism are interrelated in both of them. However, the character of magnetic interactions and spin fluctuations in ferropnictides is not reasonably described by conventional models of magnetism. Here we show that the most puzzling features can be naturally reconciled within a rather simple effective spin model with a biquadratic interaction, which is consistent with electronic structure calculations. By going beyond the Heisenberg model, our description explains numerous experimental observations, including the peculiarities of the spin-wave spectrum, thin domain walls and crossover from a first- to second-order phase transition under doping. The model also offers insight into the occurrence of the nematic phase above the antiferromagnetic phase transition.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout



Similar content being viewed by others
References
Mazin, I. I. Superconductivity gets an iron boost. Nature 464, 183–186 (2010).
Lynn, J. W. & Dai, P. Neutron studies of the iron-based family of high TC magnetic superconductors. Physica C 469, 469–476 (2009).
Johnston, D. C. The puzzle of high temperature superconductivity in layered iron pnictides and chalcogenides. Adv. Phys. 59, 803–1061 (2010).
Mazin, I. I. & Schmalian, J. Pairing symmetry and pairing state in ferropnictides: Theoretical overview. Physica C 469, 614–627 (2009).
Chandra, P., Coleman, P. & Larkin, A. I. Ising transition in frustrated Heisenberg models. Phys. Rev. Lett. 64, 88–91 (1990).
Yin, Z. P. et al. Electron–hole symmetry and magnetic coupling in antiferromagnetic LaFeAsO. Phys. Rev. Lett. 101, 047001 (2008).
Diallo, S. O. et al. Itinerant magnetic excitations in antiferromagnetic CaFe2As2 . Phys. Rev. Lett. 102, 187206 (2009).
Zhao, J. et al. Spin waves and magnetic exchange interactions in CaFe2As2 . Nature Phys. 5, 555–560 (2009).
McQueeney, R. J. et al. Anisotropic three-dimensional magnetism in CaFe2As2 . Phys. Rev. Lett. 101, 227205 (2008).
Pulikkotil, J. J., Ke, L., van Schilfgaarde, M., Kotani, T. & Antropov, V. P. Magnetism and exchange coupling in iron pnictides. Supercond. Sci. Technol. 23, 054012 (2010).
Han, M. J., Yin, Q., Pickett, W. E. & Savrasov, S. Y. Anisotropy, itineracy, and magnetic frustration in high-TC iron pnictides. Phys. Rev. Lett. 102, 107003 (2009).
Yaresko, A. N., Lin, G-Q., Antonov, V. N. & Andersen, O. K. Interplay between magnetic properties and Fermi surface nesting in iron pnictides. Phys. Rev. B 79, 144421 (2009).
Chuang, T-M. et al. Nematic electronic structure in the parent state of the iron-based superconductor Ca(Fe1xCox)2As2 . Science 327, 181–184 (2010).
Krüger, F., Kumar, S., Zaanen, J. & van den Brink, J. Spin–orbital frustrations and anomalous metallic state in iron-pnictide superconductors. Phys. Rev. B 79, 054504 (2009).
Lee, C-C., Yin, W-G. & Ku, W. Ferro-orbital order and strong magnetic anisotropy in the parent compounds of iron-pnictide superconductors. Phys. Rev. Lett. 103, 267001 (2009).
Chen, C-C., Moritz, B., van den Brink, J., Devereaux, T. P. & Singh, R. R. P. Finite-temperature spin dynamics and phase transitions in spin–orbital models. Phys. Rev. B 80, 180418(R) (2009).
Chen, C-C. et al. Orbital order and spontaneous orthorhombicity in iron pnictides. Phys. Rev. B 82, 100504 (2010).
Lv, W., Krüger, F. & Philips, P. Orbital ordering and unfrustrated (π,0) magnetism from degenerate double exchange in the iron pnictides. Phys. Rev. B 82, 045125 (2010).
Lee, C., Lin, W. & Ku, W. Unified picture for magnetic correlations in iron-based superconductors. Phys. Rev. Lett. 105, 107004 (2010).
Tanatar, M. A. et al. Uniaxial-strain mechanical detwinning of CaFe2As2 and BaFe2As2 crystals: Optical and transport study. Phys. Rev. B 81, 184508 (2010).
Fang, C., Yao, H., Tsai, W-F., Hu, J. & Kivelson, S. A. Theory of electron nematic order in LaFeAsO. Phys. Rev. B 77, 224509 (2008).
Xu, C., Müller, M. & Sachdev, S. Ising and spin orders in the iron-based superconductors. Phys. Rev. B 78, 020501(R) (2008).
Ke, L., van Schilfgaarde, M., Pulikkotil, J. J., Kotani, T. & Antropov, V. P. Low energy, coherent, Stoner-like excitations in CaFe2As2 . Phys. Rev. B 83, 060404(R) (2011).
Matveev, V. M. & Nagaev, E. L. Non-Heisenberg exchange interaction and related effects. Sov. Phys.—Solid State 14, 408 (1972).
Barzykin, V. & Gor’kov, L. P. Role of striction at magnetic and structural transitions in iron pnictides. Phys. Rev. B 79, 134510 (2009).
Nagaev, E. L. Anomalous magnetic structures and phase transitions in non-Heisenberg magnetic materials. Sov. Phys.—Usp. 25, 31–57 (1982).
Ni, N. et al. First-order structural phase transition in CaFe2As2 . Phys. Rev. B 78, 014523 (2008).
Weber, C. et al. Ising transition driven by frustration in a 2D classical model with continuous symmetry. Phys. Rev. Lett. 91, 177202 (2003).
Kapikranian, O., Berche, B. & Holovatch, Yu. Quasi-long-range ordering in a finite-size 2D classical Heisenberg model. J. Phys. A 40, 3741–3748 (2007).
Ni, N. et al. Phase diagrams of Ba(Fe1−xMx)2As2 single crystals (M=Rh and Pd). Phys. Rev. B 80, 024511 (2009).
Mun, E. D., Bud’ko, S. L., Ni, N., Thaler, A. N. & Canfield, P. C. Thermoelectric power and Hall coefficient measurements on Ba(Fe1−xTx)2As2 (T=Co and Cu) single crystals. Phys. Rev. B 80, 054517 (2009).
Fernandes, R. M. et al. Unconventional pairing in the iron arsenide superconductors. Phys. Rev. B 81, 140501(R) (2010).
Qureshi, N. et al. Crystal and magnetic structure of the oxypnictide superconductor LaO1−xFxFeAs: A neutron-diffraction study. Phys. Rev. B 82, 184521 (2010).
Li, H-F. et al. Phase transitions and iron-ordered moment form factor in LaFeAsO. Phys. Rev. B 82, 064409 (2010).
Park, J. T. et al. Symmetry of spin excitation spectra in the tetragonal paramagnetic and superconducting phases of 122-ferropnictides. Phys. Rev. B 82, 134503 (2010).
Challa, M. S. S., Landau, D. P. & Binder, K. Finite-size effects at temperature-driven first-order transitions. Phys. Rev. B 34, 1841–1852 (1986).
Binder, K. Finite size scaling analysis of Ising model block distribution functions. Z. Phys. B 43, 119–140 (1981).
Acknowledgements
We are grateful to S. L. Bud’ko and D. S. Inosov for fruitful discussions, and to I. I. Mazin for critical reading of the manuscript and useful comments. Work at UNL was supported by NSF DMR-1005642 and EPS-1010674. Work at Ames Laboratory was supported by the U.S. Department of Energy, Office of Basic Energy Sciences, Division of Materials Science and Engineering, under Contract No. DE-AC02-07CH11358. K.D.B. is a Cottrell Scholar of Research Corporation.
Author information
Authors and Affiliations
Contributions
A.L.W. carried out the thermodynamic calculations and analysed the results with K.D.B. K.D.B. and V.P.A. designed the study, carried out the spin-wave analysis and wrote the paper. All authors discussed the results.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
About this article
Cite this article
Wysocki, A., Belashchenko, K. & Antropov, V. Consistent model of magnetism in ferropnictides. Nature Phys 7, 485–489 (2011). https://doi.org/10.1038/nphys1933
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys1933
This article is cited by
-
Kondo interaction in FeTe and its potential role in the magnetic order
Nature Communications (2023)
-
Giant Dzyaloshinskii-Moriya interaction, strong XXZ-type biquadratic coupling, and bimeronic excitations in the two-dimensional CrMnI6 magnet
npj Quantum Materials (2023)
-
Electron correlation effects on exchange interactions and spin excitations in 2D van der Waals materials
npj Computational Materials (2021)
-
Biquadratic exchange interactions in two-dimensional magnets
npj Computational Materials (2020)
-
Probing the reconstructed Fermi surface of antiferromagnetic BaFe2As2 in one domain
npj Quantum Materials (2019)