Abstract
The discovery of the pseudogap in the cuprates1,2,3 created significant excitement as it was believed to be a signature of pairing4, in some cases above room temperature. Indeed, a number of experiments detected phase-fluctuating superconductivity above the transition temperature Tc (refs 5, 6, 7 8, 9). However, several recent experiments reported that the pseudogap and superconducting state are characterized by different energy scales10,11,12,13,14, and probably compete with each other15,16, leaving open the question of whether the pseudogap is caused by pair formation. Here we report the discovery of a spectroscopic signature of pair formation and demonstrate that in a region commonly referred to as the pseudogap, two distinct states coexist: one that is due to pair formation and persists to an intermediate temperature Tpair<T* and a second—the ‘proper’ pseudogap—characterized by the loss of spectral weight and anomalies in transport properties that extends up to T*. Tpair has a value around 120–150 K even for materials with very different Tc values and it probably sets a limit on the highest attainable Tc in the cuprates.
Similar content being viewed by others
Main
The traditional approach of exploring the pairing above Tc by tracking the energy scale of spectral features has so far not yielded convincing results, as these features are poorly defined above Tc. The apparent smooth evolution of the spectral gap from the lowest temperatures up to T* has previously been interpreted as key evidence for a common origin of the pseudogap and pairing gap17,18,19,20. However, very detailed, high-precision data demonstrate that the gap size actually does change across Tc (as seen in Supplementary Fig. S3). Similar behaviour is indeed expected for a system with multiple gaps (in this case a pairing gap and pseudogap), when weights of the features associated with the respective gaps change with temperature. These data provide perhaps the strongest evidence supporting a ‘two gaps’ scenario in the cuprates. A better approach is to investigate the spectral weights, which are easier to quantify and interpret. A key measure of pair formation is the density of states at the Fermi energy D(EF). In conventional, clean superconductors this weight is zero below Tc, but can be finite if there are strong impurity scattering effects. In such cases D(EF) reflects the pair-breaking states. A generic ‘density wave state’ in the absence of pairing would also lead to a decrease of the D(EF) due to the opening of the density wave gap. In addition there is also the possibility of the coexistence of superconductivity and the density wave state—inhomogeneous superconductors such as the cuprates14,21,22,23, where superconducting and non-superconducting patches coexist in the sample. One can then expect that the temperature dependence of D(EF) can be used to distinguish between these scenarios and disentangle the electronic ground states of the cuprates. In our study we use the intensity of the spectral function at EF, I(EF,k), which when integrated over all momenta equals D(EF), so the changes of one quantity with temperature are reflected in the other. This allows us to isolate the behaviour at a specific k-point and avoid smearing due to averaging. A discussion of the relation between D(EF) and I(EF,k) is provided in Supplementary Section S3.
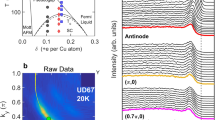
In Fig. 1a–c we examine the temperature evolution of the spectral line shape, measured at the antinodal Fermi momentum in optimally doped Bi2212 (Tc=90 K). Symmetrized energy distribution curves24 (EDCs) show the opening of the pseudogap on cooling below T* (∼210 K). As the temperature is decreased below Tc, a sharp quasiparticle peak associated with superconductivity appears25. We obtain the spectral changes with temperature by subtracting the spectrum at the highest temperature from all the spectra measured, as shown in Fig. 1b. Now we focus on the loss of spectral weight close to the Fermi level, W(EF) (hatched area in Fig. 1b). The temperature dependence of W(EF) is plotted in Fig. 1d. On cooling through T*, the spectral weight decreases linearly, which is a characteristic behaviour of the pseudogap state. An astonishing feature seen in this plot is the clear deviation from linear behaviour (indicated by the arrow). As the temperature dependence below and above this point is very different, the arrow marks the onset of another distinct state. The onset temperature Tpair (∼150 K) of this transition is considerably higher than Tc (=90 K), but is also significantly lower than the pseudogap temperature T* (∼210 K). This state probably arises from pairing of the electrons because the weight loss associated with this state smoothly evolves through Tc. If we extrapolate the linear variation of W(EF) down to T=0 K, we obtain approximate values of the spectral weight lost as a result of the pseudogap, WPG (blue area), and pairing, Wpair (red area), as marked in Fig. 1d.
a, Symmetrized EDCs (ref. 24) for various temperatures from deep below Tc to above the pseudogap temperature (T*). The spectra were measured at the antinode (marked by the red point on the Fermi surface shown in the inset) in optimally doped Bi2212 (Tc=90 K). b, Difference spectra. The spectrum measured at the highest temperature is subtracted from each of spectra in a. Spectral weight close to the Fermi level (W(EF), hatched area) is estimated by integrating the spectral intensity in b within an energy window of the experimental energy resolution (10 meV). c, The same spectra as in a with offsets. Spectral gaps are indicated with bars. d, The temperature dependence of W(EF). The pairing temperature, Tpair, is defined as the onset temperature of deviation (marked by arrow) from a linear behaviour seen at higher temperatures. The pseudogap temperature, T*, is defined to be the temperature where the two spectral peaks in the symmetrized EDCs merge into a single peak as seen in c. The three temperatures, Tc (green), Tpair (red) and T* (blue), are indicated with dashed lines. The pairing weight (Wpair, red area) and the pseudogap weight (WPG, blue area) are separated by a line extrapolated from the linear behaviour of W(EF) at high temperatures. Errors in EDC data (a–c) are statistical and reflected by noise in the data. Maximum measurement errors ±1% in d are due to uncertainty in the normalization and are smaller than data markers.
We now verify this hypothesis by studying how these quantities vary with doping in related samples of Bi2201, where Tc and T* are more separated over a wide range of carrier concentrations26. Figure 2a–g shows symmetrized EDCs measured at the antinode for various temperatures and dopings from underdoped (left side) to overdoped (right side) samples. In Fig. 1c the peak positions are marked with short black lines to demonstrate that the spectral gap changes across Tc, as discussed in the second paragraph. The spectral changes of the EDCs with temperature are plotted in Fig. 2h–n and W(EF) is plotted in Fig. 2o–u for all samples. As in the case of Bi2212 (Fig. 1), W(EF) is linear below T* at high temperatures, then suddenly deviates from a straight line—defining a new temperature scale Tpair. The temperature dependence of W(EF) evolves in a surprisingly systematic manner with doping. The linear part becomes longer with underdoping, as both T* and Tpair increase. Eventually, at the lowest dopings, W(EF) is linear down to the lowest temperature. This is because the quasiparticle residue vanishes at the antinode for heavily underdoped samples16 causing Wpair to become very small. The Tpair can be still extracted for such samples by examining W(EF,T) slightly off the antinode. In case of UD23K Tpair is ∼125 K.
a–g, Symmetrized EDCs at various temperatures measured at the antinode (marked by the red point on the Fermi surface shown in the inset of o) in Bi2201 over a wide range of doping from underdoping (left) to overdoping (right). An offset is used for clarity. h–n, Difference spectra. The spectrum at the highest temperature is subtracted from each of the spectra in a–g. o–u, Temperature dependence of the spectral weight close to EF, W(EF), obtained by integrating the spectra in h–n within the energy resolution window (10 meV) about EF (see Fig. 1b). The three temperatures, Tc (green), Tpair (red) and T* (blue), are indicated with dashed lines. The pairing weight (Wpair, red area) and the pseudogap weight (WPG, blue area) are separated by a line extrapolated from the linear behaviour of W(EF) at high temperatures. Error bars in EDC curves (a–n) are statistical and reflected by noise in the data. Maximum measurement errors ±1% in o–u are due to uncertainty in the normalization and are smaller than data markers.
To validate our assertion about the pairing origin of Wpair, we extract this quantity for each doping by subtracting the interpolated WPG line from each of the W(EF,T) curves and compare them in Fig. 3a. Obviously the magnitude and onset temperature of Wpair is very different for each doping. To make a fair comparison, we rescale the vertical axis for each curve by its maximum value at the lowest temperature and the horizontal axis by Tpair. Surprisingly the curves for all dopings fall on top of each other, demonstrating a universal scaling of Wpair, which smoothly evolves through Tc. Clearly, W(EF,T) in the superconducting state reflects pair formation, which causes it to decrease on cooling. The temperature dependence of Wpair does not exhibit significant features at Tc and its scaling remains unchanged across Tc, strongly suggesting that pair formation occurs well above Tc. As Wpair scales with Tpair, this must be the onset temperature of pairing. At the lowest dopings (Fig. 2o), W(EF,T) is a linear function of temperature. We attribute this behaviour to the pseudogap, because it was demonstrated that the antinode in underdoped samples is dominated by the pseudogap and does not contribute to the superfluid density15,16. This almost perfect scaling behaviour of Wpair with Tpair not only validates our extraction of the pairing component, but it also gives compelling evidence that Tpair is the onset temperature of pairing and that pairing is not the origin of the pseudogap, because the pseudogap persists to the much higher T*.
a, Temperature dependence of (Wpair) for all samples extracted by subtracting the extrapolated WPG line from the W(EF) curves in Fig. 2h–n. b, Wpair from a scaled with the pairing temperature (Tpair) and the maximum value at the lowest temperature (WpairMax). Maximum measurement errors ±1% in a and b are due to uncertainty in the normalization and are smaller than the data markers.
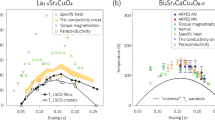
We summarize our results in Fig. 4 in the form of a phase diagram. We compare our data to the detection of phase-fluctuating superconductivity by magnetization6, the Nernst effect5, NMR (ref. 26) and specific heat27. We note the reasonable agreement between these probes and angle-resolved photoemission spectroscopy (ARPES). Note that ARPES reports slightly different temperatures, because the other probes are sensitive to a weighted average over the Fermi surface, whereas with ARPES we can extract these directly for the antinodal areas, where this temperature is expected to be highest. We note that specific-heat results27 were carried out using Bi2212 samples and exhibit slightly higher pairing fluctuation temperatures, in agreement with our Bi2212 results in Fig. 1. The pairing temperature (Tpair) (shown in Fig. 4b) increases steadily from the overdoped side of the phase diagram towards optimal doping. For dopings lower than optimal, it levels off at ∼120 K. This behaviour contrasts with that of the pseudogap temperature (T*) (Fig. 4c), which monotonically increases up to the lowest doping. We note that the pairing temperature of Bi2201 is similar to that of Bi2212 (see Fig. 1d), despite the large difference of Tc. This strongly suggests that the onset temperature of pairing (120–150 K) is universal and similar to the highest achieved superconducting temperature in the cuprates. Quantitative analysis of the very detailed ARPES data presented here provides clear evidence for a spectroscopic temperature scale Tpair, distinct from Tc and T*. It demonstrates that pairing and the pseudogap are two fundamentally different states. The competition between the two states may play a key role in the determination of Tc, where bulk superconductivity is established.
a, W(EF) versus T plots for OD31K, the same as Fig. 2r. b, Phase diagram obtained using the pairing spectral weight (Wpair, red area in a). The onset temperature of pair formation estimated from our ARPES data (Tpair), the onset temperature of the Nernst effect5 (Tυ), the diamagnetic effect6 (TM) and specific heat27 (Tmf) are plotted for comparison. As the specific-heat measurements were carried out using Bi2221, the horizontal axis for Tmf plots was scaled by the ratio of Tc values for Bi2212 and Bi2201. Note that Tpair for UD23K was extracted from data around 13° off the antinode because both quasiparticle peaks and Wpair are very small at the antinode. c, Phase diagram obtained using the pseudogap spectral weight (WPG, blue area in a). The pseudogap temperature estimated from our ARPES data (T*), our resistivity results (Tρ, see Supplementary Fig. S1) and NMR (TNMR; ref. 26) are plotted. Error bars in b represent uncertainty in estimating the temperatures at which deviation from linear behaviour occurs (obtained by interpolation from errors in W(EF). Error bars in c represent uncertainty in estimating the temperature at which the pseudogap closes (that is, two peaks merge into a single peak at EF. Experimental errors in a are the same as in Fig. 1d.
The remaining open question is the origin of the pseudogap. Recent results from scanning tunnelling microscopy (STM) suggested23,28 that the pseudogap is associated with a ‘checkerboard’ pattern29. Although direct evidence for this (for example, vanishing of the ‘checkerboard’ pattern at T*) is still missing, our data seem to support this scenario. Figure 3d of ref. 30 shows the relation between a ‘checkerboard’ wave vector and pseudogap energy. The average binding energies (represented by black data points), for which the ‘checkerboard’ is observed in STM measurements agrees with the values of the pseudogap we find for the same samples with ARPES. There is also no STM evidence for a ‘checkerboard’ pattern in overdoped samples, where the pseudogap is absent.
The fact that we observe perfect scaling of Wpair with Tpair, regardless of the doping, implies that the only two relevant energy scales are the order parameter of the pseudogap state and the magnitude of the pairing potential, making the existence of the three temperature scales Tc<Tpair<T*, a universal aspect of underdoped cuprates. The observed scaling behaviour with respect to Tpair indicates a breakdown of the classical picture of phase fluctuations in the cuprates and gives an important clue as to the nature of the Cooper-pair fluctuations: it is not sufficient to solely consider phase fluctuations of the pairing field. Tpair is the temperature where the amplitude of the pairing field melts, that is, where the strength of incoherent pairing disappears. The emergence of Tpair as the relevant temperature of the scaling requires that the pair-amplitude and phase fluctuation are equally crucial below Tpair. A pairing interaction that is in the extreme strong-coupling limit, reminiscent of Mott physics, was shown to lead to simultaneous amplitude and pair modes that separate coherent and local pairing30.
Methods
Optimally doped Bi2Sr2CaCu2O8+δ (Bi2212) single crystals with Tc=90 K (OP90K) and (Bi,Pb)2(Sr,La)2CuO6+δ(Bi2201) single crystals with various Tc values were grown by the conventional floating-zone technique (see Supplementary Information on the sample characterization). To precisely analyse the ARPES spectra, we partially substituted Pb for Bi for all Bi2201 samples, and suppressed the modulation in the BiO plane, which usually contaminates the ARPES signal. ARPES data were acquired using a laboratory-based system consisting of a Scienta SES2002 electron analyser and a GammaData helium ultraviolet lamp. All data were acquired using the HeI line with a photon energy of 21.2 eV. The angular resolution was 0.13° and ∼0.5° along and perpendicular to the direction of the analyser slits, respectively. The energy resolution was set at ∼10 meV—confirmed by measuring the energy width between the 90% and 10% of the Fermi edge from the same Au reference. Custom-designed refocusing optics enabled us to accumulate high-statistics spectra in a short time without effects of sample surface ageing. In the analysis we used symmetrized EDCs normalized to the total area over the whole energy range (−0.4 eV≤E≤0.4 eV) for each spectrum. We verified that the choice of normalization scheme does not affect the results of our analysis (see Supplementary Information on the details). The results were reproduced on several samples and on temperature cycling.
References
Warren, W. W. et al. Cu spin dynamics and superconducting precursor effects in planes above Tc in YBa2Cu3O6.7 . Phys. Rev. Lett. 62, 1193–1196 (1989).
Takigawa, M. et al. Cu and O NMR-studies of the magnetic properties of YBa2Cu3O6.63 (Tc=62 K). Phys. Rev. B 43, 247–257 (1991).
Homes, C. C., Timusk, T., Liang, R., Bonn, D. A. & Hardy, W. N. Optical conductivity of c-axis oriented YBa2Cu3O6.70—evidence for a pseudogap. Phys. Rev. Lett. 71, 1645–1648 (1993).
Emery, V. J. & Kivelson, S. A. Importance of phase fluctuations in superconductors with small superfluid density. Nature 374, 434–437 (1995).
Wang, Y. et al. Onset of the vortexlike Nernst signal above Tc in La2−xSrxCuO4 and Bi2Sr2−yLayCuO6 . Phys. Rev. B 64, 224519 (2001).
Lu, Li et al. Diamagnetism and Cooper pairing above Tc in cuprates. Phys. Rev. B 81, 054510 (2010).
Lee, J. et al. Spectroscopic fingerprint of phase-incoherent superconductivity in the underdoped Bi2Sr2CaCu2O8+δ . Science 325, 1099–1103 (2009).
Corson, J., Mallozzi, R., Orenstein, J., Eckstein, J. N. & Bozovic, I. Vanishing of phase coherence in underdoped Bi2Sr2CaCu2O8+δ . Nature 398, 221–223 (1999).
Bergeal, N. et al. Pairing fluctuations in the pseudogap state of copper-oxide superconductors probed by the Josephson effect. Nature Phys. 4, 608–611 (2008).
Panagopoulos, C. & Xiang, T. Relationship between the superconducting energy gap and the critical temperature in high-Tc superconductors. Phys. Rev. Lett. 81, 2336–2339 (1998).
Tanaka, K. et al. Distinct Fermi-momentum-dependent energy gaps in deeply underdoped Bi2212. Science 314, 1910–1913 (2006).
Le Tacon, M. et al. Two energy scales and two distinct quasiparticle dynamics in the superconducting state of underdoped cuprates. Nature Phys. 2, 537–543 (2006).
Kondo, T., Takeuchi, T., Kaminski, A., Tsuda, T. & Shin, S. Evidence for two energy scales in the superconducting state of optimally doped (Bi,Pb)2(Sr,La)2CuO6+δ . Phys. Rev. Lett. 98, 267004 (2007).
Boyer, M. C. et al. Imaging the two gaps of the high-temperature superconductor Bi2Sr2CuO6+x . Nature Phys. 3, 802–806 (2007).
Khasanov, R. et al. Evidence for competition between the superconducting and the pseudogap state in (BiPb)2(SrLa)2CuO6+x from muon-spin rotation experiments. Phys. Rev. Lett. 101, 227002 (2008).
Kondo, T., Khasanov, R., Takeuchi, T., Schmalian, J. & Kaminski, A. Competition between the pseudogap and superconductivity in the high-Tc copper oxides. Nature 457, 296–300 (2009).
Ding, H. et al. Spectroscopic evidence for a pseudogap in the normal state of underdoped high-Tc superconductors. Nature 382, 51–54 (1996).
Loeser, A. G. et al. Excitation gap in the normal state of underdoped Bi2Sr2CaCu2O8+x . Science 273, 325–329 (1996).
Meng, J. et al. Motonic d-wavesupercondcuting gap in optimally-doped Bi2Sr1.6La0.4CuO6+δ superconductor by laser-based angle-resolved photoemission spectroscopy. Phys. Rev. B 79, 024514 (2009).
Nakayama, K. et al. Evolution of a pairing-induced pseudogap from the superconducting gap of Bi2Sr2CuO6+δ . Phys. Rev. Lett. 102, 227006 (2009).
Pan, S. H. et al. Microscopic electronic inhomogeneity in the high-Tc superconductor Bi2Sr2CaCu2O8+x . Nature 413, 282–285 (2001).
Gomes, K. K. et al. Visualizing pair formation on the atomic scale in the high-Tc superconductor Bi2Sr2CaCu2O8+δ . Nature 447, 569–572 (2007).
Wise, W. D. et al. Charge-density-wave origin of cuprate checkerboard visualized by scanning tunnelling microscopy. Nature Phys. 4, 696–699 (2008).
Norman, M. R. et al. Destruction of the Fermi surface in underdoped high-Tc superconductors. Nature 392, 157–160 (1998).
Wei, J. et al. Superconducting coherence peak in the electronic excitations of a single layer cuprate superconductor Bi2Sr1.6La0.4CuO6+δ . Phys. Rev. Lett. 101, 097005 (2008).
Zheng, G., Kuhns, P. L., Reyes, A. P., Liang, B. & Lin, C. T. Critical point and the nature of the pseudogap of single-layered copper-oxide Bi2Sr2−xLaxCuO6+δ superconductors. Phys. Rev. Lett. 94, 047006 (2005).
Tallon, J. L. et al. Fluctuations and Tc reduction in cuprate superconductors. Preprint at http://arxiv.org/abs/0908.4428 (2009).
Wise, W. D. et al. Imaging nanoscale Fermi-surface variations in an inhomogeneous superconductor. Nature Phys. 5, 213–216 (2009).
Hanaguri, T. et al. A ‘checkerboard’ electronic crystal state in lightly hole-doped Ca2−xNaxCuO2Cl2 . Nature 430, 1001–1005 (2004).
Chubukov, A. V. & Schmalian, J. Superconductivity due to massless boson exchange in the strong-coupling limit. Phys. Rev. B 72, 174520 (2005).
Acknowledgements
We thank A. Millis, C. Varma and M. Norman for useful discussions. This work was supported by Basic Energy Sciences, US DOE. The Ames Laboratory is operated for the US DOE by Iowa State University under Contract No. W-7405-ENG-82. Work at Brookhaven is supported by the US DOE under Contract No. DE-AC02-98CH10886. J.S.W. and Z.J.X. are supported by the Center for Emergent Superconductivity, an Energy Frontier Research Center funded by the US DOE, Office of Science.
Author information
Authors and Affiliations
Contributions
T.K. and A.K. designed the experiment. T.K., Y.H., T.T., J.S.W., Z.J.X. and G.G. grew the high-quality single crystals. T.K. and A.D.P. acquired the experimental data and T.K. carried out the data analysis. T.K., A.K. and J.S. wrote the manuscript. All authors discussed the results and commented on the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Information (PDF 946 kb)
Rights and permissions
About this article
Cite this article
Kondo, T., Hamaya, Y., Palczewski, A. et al. Disentangling Cooper-pair formation above the transition temperature from the pseudogap state in the cuprates. Nature Phys 7, 21–25 (2011). https://doi.org/10.1038/nphys1851
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys1851
This article is cited by
-
Prominent Josephson tunneling between twisted single copper oxide planes of Bi2Sr2-xLaxCuO6+y
Nature Communications (2023)
-
Puddle formation and persistent gaps across the non-mean-field breakdown of superconductivity in overdoped (Pb,Bi)2Sr2CuO6+δ
Nature Materials (2023)
-
Unconventional spectral signature of Tc in a pure d-wave superconductor
Nature (2022)
-
Signature of Kondo hybridisation with an orbital-selective Mott phase in 4d Ca2−xSrxRuO4
npj Quantum Materials (2022)
-
Paramagnons and high-temperature superconductivity in a model family of cuprates
Nature Communications (2022)