Abstract
Harmonic generation is a general feature of driven nonlinear systems. In particular high-order harmonic generation (HHG) in atomic gases1 is the basis for producing attosecond pulses2,3. In molecules and clusters, the existence of multiple ionization and recombination sites makes for richer dynamics allowing imaging of molecular orbitals4,5, higher conversion efficiency6 and the possibility of extending the high-energy cutoff7. In the strong-field limit, HHG in bulk crystals is fundamentally different from that in the atomic case owing to the high density and periodic structure. Here we present the first observation of HHG in a bulk crystalline solid using a long-wavelength few-cycle laser. The harmonics spectra extend well beyond the band edge of the ZnO crystal, show a clear non-perturbative character and exhibit a cutoff that scales linearly with the electric field of the drive laser. Our results have important implications for the understanding of attosecond electron dynamics and other non-equilibrium band-structure-related phenomena in strongly driven bulk solids.
Similar content being viewed by others
Main
The HHG spectrum from a gas typically comprises a region of rapidly decreasing low orders that scale perturbatively followed by a slowly varying succession of higher orders that scale non-perturbatively with the strength of the drive laser1. At the tunnelling limit of strong-field ionization8, the non-perturbative harmonic generation process has been described semiclassically in a recollision model9,10 consisting of three steps: tunnel ionization of an electron, its acceleration in the laser field, and its recombination to the parent ion with an energy release in the form of higher-energy photons—a coherent process that occurs on successive half-cycles of the laser pulse, leading to emission of odd harmonics. The single-atom maximum photon energy is9,11 ℏωmax=Ip+3.2Up, where Ip is the ionization potential and Up=e2E2λ2/16π2m c2 is the ponderomotive energy of the electron in the laser field. The amplitude of the maximum excursion of a recolliding electron is rmax=e E λ2/4π2m c2. For the conditions of our experiments, E=0.6 V Å−1 at λ=3.25 μm, the atomic case would be Up=5 eV and rmax=32 Å. The latter is many times the lattice constant of a typical crystal. Thus, we expect the possibility of ionization from one site and recombination on another; however, because of the lattice periodicity the process would still be coherent. We note that at this field strength, the potential across a lattice constant is comparable to the bandgap of a typical insulator. Therefore, the field cannot be thought of as a small perturbation to the crystal. The non-perturbative HHG from bulk crystals has been considered theoretically12,13,14 but has never been observed experimentally until now.
Previously, experimental observation of non-perturbative HHG in solids was only in reflection geometry15,16,17,18. In transmission, perturbative harmonics below the band edge up to the seventh order were produced by exciting semiconducting ZnSe with a maximum field strength of ∼0.08 V Å−1 at a central wavelength of 3.9 μm (ref. 19). Similarly, excitation of liquid water by stronger pulses resulted in harmonics up to the 13th order at a central wavelength of 3.66 μm (ref. 20). Measurement of higher orders at strong-field (approaching 1 V Å−1) drive is limited by both the material damage and absorption of the high-energy photons by the dense media. The damage at this limit is mainly thought to be due to the multiphoton absorption and tunnel ionization21. We note the single-shot ablation threshold for ZnO is 0.6 V Å−1 when using 70 fs pulses at 0.8 μm centre wavelength22. Here we use a longer wavelength drive, centred at 3.25 μm, and are able to drive the system with the same field at 1 kHz without imposing physical damage. A higher threshold for a longer wavelength drive is probably due to the smaller photoabsorption cross-section in the case of high-order processes. At least nine photons are required for an excitation from the valance to the conduction band in ZnO in the case of 3.25 μm drive, unlike only two to three for 0.8 μm drive.
In the experiments, high-power, ∼9-cycle, wavelength-tunable (∼3.2 μm to ∼3.7 μm) mid-infrared laser pulses are produced by difference-frequency generation between a femtosecond Ti:sapphire laser and a picosecond Nd:YLF laser, providing up to ∼100 μJ per pulse at 1 kHz (ref. 23). The linear polarized mid-infrared light is focused with f/3 optics on a single-crystal ZnO wafer near normal incidence. ZnO is a non-centrosymmetric uniaxial crystal (wurtzite structure) with its optic axis along the hexagonal c axis. The crystal is mounted to allow rotation about its normal and translation through the laser focus. The laser focus is imaged using f/4 reflective optics on to the slit of a spectrometer (Acton SP300i) with a 150 g mm−1 grating and an intensified CCD (charge-coupled device) camera (ICCD, PI-MAX1024UV). The entire high-harmonic set-up is in a sealed container that is continuously purged with Ar gas. Thus, it is capable of detecting ultraviolet wavelengths down to ∼115 nm, limited by the transmission of the MgF2 window on the ICCD.
Figure 1a is representative spectra showing odd-order harmonics generated in a 500-μm-thick ZnO crystal cut perpendicular to its optic axis. The grating angle is set such that the low-energy end of the detection is approximately at the ZnO band edge (∼3.2 eV). The presence of harmonics above the bandgap suggests that the generation is limited to the last few tens of nanometres of material (assuming linear absorption of the harmonics corresponding to the field-free case). The spectra also show fluorescence due to electron–hole recombination. Unlike the harmonics, the fluorescence is long-lived as verified by delaying the electronic gate on the ICCD. The two spectra shown are taken at different pulse energies. The lower-pulse-energy (0.52 μJ) spectrum extends up to the 17th order, whereas the higher-pulse-energy (2.63 μJ) spectrum extends further to the 25th order. We note that the higher pulse energy is the limit where the crystal can be repeatedly driven at 1 kHz without imposing physical damage. This corresponds to a peak intensity of ∼5 TW cm−2 (field strength of ∼0.6 V Å−1). The peak intensity is the vacuum intensity estimated by measuring the photoelectron energy spectrum in gas-phase experiments24 using the same focusing geometry. Figure 1b shows the measured high-energy cutoff as a function of the drive-laser field. We find that the cutoff scales linearly with the field. This is a striking difference from the atomic case where the scaling is quadratic in the field11,25. Finally, we note that for moderate pulse energies, the spectra are only weakly dependent on the position of the focus; however, for the higher pulse energies the spectra are dominated by the fluorescence as we focus towards the front surface and by the harmonics peaks with better modulation depth as we focus towards the back surface of the crystal.
a, Spectra from a 500-μm-thick ZnO crystal where the optic axis is perpendicular to the surface. The wavelength of the driving field is centred at 3.25 μm. The spectra represented by the green and blue curves are for driving pulse energies of 0.52 μJ and 2.63 μJ, corresponding to an estimated vacuum field strength of 0.27 V Å−1 and 0.6 V Å−1, respectively. The inset shows the expanded view at and near the cutoff of the 2.63 μJ spectrum on a linear scale. The dotted vertical line marks the approximate band edge of the crystal as indicated by the residual fluorescence signal. b, The high-energy cutoff scales linearly with drive-laser field.
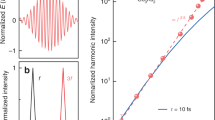
The non-perturbative character of the high-order harmonics can be clearly seen in the scaling of the individual harmonic peaks with drive intensity. Figure 2 shows how the harmonic peaks HO 9–21 scale as a function of estimated drive-laser intensity from 0.5 to 5 TW cm−2 (field strength from 0.2 to 0.6 V Å−1) on a logarithmic scale. We note that in the perturbative regime, the harmonics would scale with the order of the process. For comparison, we show this scaling for a 15th-order process. At lower intensities, the harmonics are highly nonlinear with a similar intensity dependence irrespective of order, whereas at higher intensities the scaling is much closer to a linear scale.
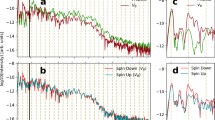
The HHG spectra show no qualitative differences as a function of the mid-infrared polarization direction for propagation along the optic axis. This is not the case for a crystal with the optic axis in the plane of the surface, which shows strong polarization effects. Figure 3 shows the measured harmonic spectra as a function of the angle between the laser polarization and the optic axis. Note that in general both odd and even harmonics are generated, whereas only odd harmonics are generated when propagating along the optic axis. The odd and even harmonics show their maxima every 90° and every 180° of rotation, respectively. The two-fold symmetry of the even harmonics is consistent with the inversion symmetry breaking along the c axis. This is strong evidence that the source of the harmonics is in fact the bulk periodic solid. We further note that for orientations where the input polarization is not parallel or perpendicular to the optic axis, the laser polarization becomes elliptical on propagation.
Spectra for HHG in a 500-μm-thick ZnO crystal with the optic axis parallel to the surface. The crystal is rotated about its normal to vary the angle between the incident laser polarization and the optic axis. The field strength is 0.6 V Å−1, and the wavelength of the driving field is centred at 3.25 μm. The odd and even harmonics appear every 90° and 180° respectively whereas the fluorescence signal remains isotropic. The intensity is shown in false colour on a natural-log scale in otherwise arbitrary units. The grating angle is set such that both below- and above-gap harmonics are observed.
We study the ellipticity dependence of HHG for the case of propagation along the optic axis (that is, in the absence of the crystal birefringence) using a quarter-waveplate to set the polarization. In this particular case, the measurement is carried out at ambient conditions using a spectrometer (TRIAX 180 with 1024MSA ICCD) that covers from ∼800 nm to ∼200 nm wavelength range, and the drive-laser central wavelength is tuned to 3.66 μm to match the retardation of the available waveplate. Figure 4 shows the results for linear, elliptical and circular polarization, as indicated in the legend. We find that unlike in the gas phase25, overall the harmonics here are less sensitive to the ellipticity, requiring a circular polarization to effectively turn off the HHG process, despite the strong-field ionization (as evidenced by the fluorescence at the band edge). The relative insensitivity of the harmonics to ellipticity is an indication that the process is not limited to ionization and recombination on the same site.
Spectra from a 500-μm-thick ZnO crystal with its optic axis perpendicular to the surface as a function of the ellipticity (ε) of the laser. The field strength is 0.6 V Å−1, and the wavelength of the driving field is centred at 3.66 μm.The ellipticity seems to more strongly affect the higher orders, with circular polarization effectively turning off all orders. The fluorescence, roughly centred on the ninth order, persists even for the circular polarization.
For illustrative purposes, we consider a simple model that shows how non-perturbative HHG could arise in a solid owing to periodically modulated Bloch oscillations. For oscillations in a single cosine band, the harmonics of the drive frequency are expected to extend on the order of ωB/ω (ref. 12), where ωB=e E d/ℏ is the corresponding Bloch frequency for Bragg scattering of an electron of charge e from a lattice of periodicity d for a peak electric field, E. However, in our experiments, we detect harmonics up to the 25th order for conditions when ωB/ω∼5. A more realistic description for the mechanism would include the dressed band structure with both intra- and inter-band transitions as well as propagation effects. Despite these complications, in what follows we will see that a model for acceleration in a single non-cosine band allows much higher-order harmonics and captures the general features of measured HHG spectra including the linear scaling of the cutoff with applied field.
We consider a one-dimensional band,  . The acceleration of a small electron density N centred at k=0 at the peak of the electric field, Ecos(ω t), will produce a nonlinear current density,
. The acceleration of a small electron density N centred at k=0 at the peak of the electric field, Ecos(ω t), will produce a nonlinear current density,

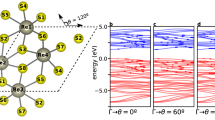
where m* is the band effective mass at k=0, bn=cnd2m*/ℏ2 are scaled Fourier coefficients of the band and Jl is a Bessel function of the first kind of order l. We write the time-dependent current in a form reminiscent of Ohm’s law, but it is clearly nonlinear, with a spectrum comprising odd harmonics of the driving frequency that will subsequently radiate. Figure 5a–d shows the normalized drive field, nonlinear current, the electron trajectory and corresponding spectrum for the time-varying current when ωB/ω=5. We choose a primarily cosine band with a small third spatial harmonic component (ε(k)=2.5(1–0.95cosk d−0.05cos3k d) (eV)), where  . This approximates the first conduction band of ZnO along
. This approximates the first conduction band of ZnO along  –M as calculated using the non-local empirical pseudopotential method in ref. 26. Figure 5d also shows the calculated spectra for a cosine band (ε(k)=2.5(1−cosk d) (eV)) demonstrating the sensitivity of the spectrum to the small variation in the band structure. Evidently the harmonic content in the current is due to a combination of Bragg scattering near the peaks of the electric field along with anharmonic motion in the band, all of which repeats every half-cycle of the laser field. The contribution to the current for spatial frequency n k scales non-perturbatively for sufficiently high fields, resulting in a plateau extending to harmonic order (2s−1)n≈n e E d/ℏω. Thus, the high-energy cutoff will scale linearly with the field—in agreement with our experimental results. Finally, we note that the absence of even harmonics in this model is a consequence of the inversion symmetry of the bands and the semiclassical equations of motion; although, in a non-centrosymmetric material, a finite Berry’s phase on Bragg scattering leads to a correction in the equations of motion27 that could allow for the even harmonics.
–M as calculated using the non-local empirical pseudopotential method in ref. 26. Figure 5d also shows the calculated spectra for a cosine band (ε(k)=2.5(1−cosk d) (eV)) demonstrating the sensitivity of the spectrum to the small variation in the band structure. Evidently the harmonic content in the current is due to a combination of Bragg scattering near the peaks of the electric field along with anharmonic motion in the band, all of which repeats every half-cycle of the laser field. The contribution to the current for spatial frequency n k scales non-perturbatively for sufficiently high fields, resulting in a plateau extending to harmonic order (2s−1)n≈n e E d/ℏω. Thus, the high-energy cutoff will scale linearly with the field—in agreement with our experimental results. Finally, we note that the absence of even harmonics in this model is a consequence of the inversion symmetry of the bands and the semiclassical equations of motion; although, in a non-centrosymmetric material, a finite Berry’s phase on Bragg scattering leads to a correction in the equations of motion27 that could allow for the even harmonics.
The dispersion is taken to be ε(k)=2.5(1−0.95cosk d−0.05cos3k d) (eV), and the field strength of the laser is such that ωB=5ω. a, Normalized field. b, Nonlinear current in units of the linear conductivity times the peak field. c, Electron trajectory in units of d. d, The harmonic content of the current for the non-cosine band in blue and for a pure cosine band in green, also in units of the linear conductivity times the peak field.
We demonstrate a first experimental observation of non-perturbative HHG in a strongly driven wide-bandgap (3.2 eV) semiconductor using mid-infrared (0.34–0.38 eV) few-cycle laser pulses. We measure harmonics up to the 25th order, extending to 9.5 eV—more than 6 eV above the band edge. We find that the high-energy cutoff scales linearly with the driving field in contrast to that in the atomic case where the scaling is linear to the intensity. The spectrum comprises odd, or odd and even, harmonics depending on crystallographic orientation. We find that harmonics are less sensitive to the ellipticity of the driving field as compared with that from isolated atoms and molecules. The HHG spectrum from the bulk has an imprint of the band structure of a periodic solid. Therefore, in addition to the studies of ultrafast dynamics of electrons in a periodic solid, one can use the HHG spectra to explore the dressed band structure in the strong-field limit28.
References
Ferray, M. et al. Multiple-harmonic conversion of 1064 nm radiation in rare gases. J. Phys. B 21, L31–L35 (1988).
Drescher, M. et al. X-ray pulses approaching the attosecond frontier. Science 291, 1923–1927 (2001).
Paul, P. M. et al. Observation of a train of attosecond pulses from high harmonic generation. Science 292, 1689–1692 (2001).
Smirnova, O. et al. High harmonic interferometry of multi-electron dynamics in molecules. Nature 460, 972–977 (2009).
Itatani, J. et al. Tomographic imaging of molecular orbitals. Nature 432, 867–871 (2004).
Ditmire, T., Donnelly, T. D., Falcone, R. W. & Perry, M. D. Strong X-ray emission from high-temperature plasmas produced by intense irradiation of clusters. Phys. Rev. Lett. 75, 3122–3125 (1995).
Lein, M. & Rost, J. M. Ultrahigh harmonics from laser-assisted ion-atom collisions. Phys. Rev. Lett. 91, 243901 (2003).
Keldysh, L. V. Ionization in the field of a strong electromagnetic wave. J. Exp. Theor. Phys. 47, 1945–1957 (1965).
Schafer, K. J., Yang, B., DiMauro, L. F. & Kulander, K. C. Above threshold ionization beyond the high harmonic cutoff. Phys. Rev. Lett. 70, 1599–1603 (1993).
Corkum, P. Plasma perspective on strong field multiphoton ionization. Phys. Rev. Lett. 71, 1994–1997 (1993).
Krause, J. L., Schafer, K. J. & Kulander, K. C. High-order harmonic generation from atoms and ions in the high intensity regime. Phys. Rev. Lett. 68, 3535–3538 (1992).
Golde, D., Meier, T. & Koch, S. W. High harmonics generated in semiconductor nanostructures by the coupled dynamics of optical inter- and intraband excitations. Phys. Rev. B 77, 075330 (2008).
Faisal, F. H. M. & Kamiński, J. Z. Floquet-Bloch theory of high-harmonic generation in periodic structures. Phys. Rev. A 56, 748–762 (1997).
Gupta, A. K., Alon, O. E. & Moiseyev, N. Generation and control of high-order harmonics by the interaction of an infrared laser with a thin graphite layer. Phys. Rev. B 68, 205101 (2003).
Burnett, N. H., Baldis, H. A., Richardson, M. C. & Enright, G. D. Harmonic generation in CO2 laser target interaction. Appl. Phys. Lett. 31, 172–174 (1977).
Carman, R. L., Forslund, D. W. & Kindel, J. M. Visible harmonic emission as a way of measuring profile steepening. Phys. Rev. Lett. 46, 29–32 (1981).
von der Linde, D. et al. Generation of high-order harmonics from solid surfaces by intense femtosecond laser pulses. Phys. Rev. A 52, R25–R27 (1995).
Norreys, D. et al. Efficient extreme UV harmonics generated from picosecond laser pulse interactions with solid targets. Phys. Rev. Lett. 76, 1832–1835 (1996).
Chin, A. H., Calderon, O. G. & Kono, J. Extreme midinfrared nonlinear optics in semiconductors. Phys. Rev. Lett. 86, 3292–3295 (2001).
DiChiara, A. D., Sistrunk, E., Miller, T. A., Agostini, P. & DiMauro, L. F. An investigation of harmonic generation in liquid media with a mid-infrared laser. Opt. Express 17, 20959–20965 (2009).
Schaffer, C., Brodeur, A. & Mazur, E. Laser-induced breakdown and damage in bulk transparent materials induced by tightly focused femtosecond laser pulses. Meas. Sci. Technol. 12, 1784–1794 (2001).
Li, C. et al. Ultrafast dynamics in ZnO thin films irradiated by femtosecond lasers. Solid State Commun. 136, 389–394 (2005).
Schultz, K. D. et al. Strong-field physics with mid-infrared lasers. J. Mod. Opt. 54, 1075–1085 (2007).
Blaga, C. I. et al. Strong-field photoionization revisited. Nature Phys. 5, 335–338 (2009).
Shan, B., Ghimire, S. & Chang, Z. Effect of orbital symmetry on high-order harmonic generation from molecules. Phys. Rev. A 69, 021404 (2004).
Goano, M., Bertazzi, F., Penna, M. & Bellotti, E. Electronic structure of wurtzite ZnO: Nonlocal pseudopotential and ab initio calculations. J. Appl. Phys. 102, 083709 (2007).
Zak, J. Berry’s phase for energy bands in solids. Phys. Rev. Lett. 62, 2747–2750 (1989).
Tzoar, N. & Gersten, J. I. Theory of electronic band structure in intense laser fields. Phys. Rev. B 12, 1132–1139 (1975).
Acknowledgements
S.G. and D.A.R. are supported through the PULSE Institute at the SLAC National Accelerator Laboratory by the US Department of Energy, Office of Basic Energy Science. The work conducted at OSU is financially supported by DOE contracts DE-FG02-06ER15833 and DE-FG02-04ER15614. We acknowledge many stimulating discussions with K. Schafer.
Author information
Authors and Affiliations
Contributions
S.G. and D.A.R. planned and carried out the experiment, analysed the data and wrote the manuscript. A.D.D. and E.S. took data and contributed to the data analysis and planning of the experiment. P.A. and L.F.D. contributed to the planning of the experiment.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
About this article
Cite this article
Ghimire, S., DiChiara, A., Sistrunk, E. et al. Observation of high-order harmonic generation in a bulk crystal. Nature Phys 7, 138–141 (2011). https://doi.org/10.1038/nphys1847
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys1847
This article is cited by
-
Attosecond-resolved non-dipole photoionization dynamics
Nature Photonics (2024)
-
Maximizing the efficiency of intrapulse difference frequency generation by pulse shaping and recycling
Applied Physics B (2024)
-
Attosecond Physics in a Nutshell
Resonance (2024)
-
Light control with Weyl semimetals
eLight (2023)
-
Light emission from strongly driven many-body systems
Nature Physics (2023)