Main

In coupling two qubits one can distinguish interactions that are oriented either along or perpendicular to the eigenstates of the qubits. Although in both cases the resulting two-qubit energy-level spectrum reflects the coupling strength, the response to a change of the state of a qubit differs greatly. With longitudinal coupling the state of one qubit affects the energy splitting of the other qubit. Although this spectroscopic shift enables simple resonant driving for all operations7,8, in practice it requires refocusing schemes to compensate for the continuously evolving phases9. In contrast, for transverse coupling the energy splitting of one qubit does not depend on the state of the other qubit. This last case is appealing, as in the absence of driving the system acts as a set of uncoupled qubits, and the coupling is effectively switched on when a.c. driving is applied10. The price to pay for the advantage of transverse coupling is obvious; the degeneracy prohibits schemes for selective excitation that rely on a frequency splitting. Previous experiments used either extra coupling elements11, extra modes12 or shifted levels into and out of resonance by d.c. (ref. 13) or strong a.c. fields14,15. Note that level shifting can imply passing through conditions of low coherence16, or passing resonances with other qubits. In contrast, our method works for simple direct coupling as well as for systems with extra coupling elements, such as harmonic oscillators, as long as the effective coupling is transverse. It uses only a single pulse of a single frequency and does not require (dynamical) shifting of the levels.

We consider the class of systems of transversely coupled qubits, described with the Hamiltonian

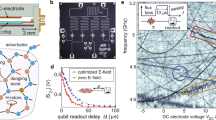
where Δi is the single-qubit energy splitting of qubit i, , J is the qubit–qubit coupling energy and σx,y,zi are the Pauli spin matrices. This Hamiltonian describes many actively used quantum systems1,2,3,4,5,6, and often applies for operation at a coherence sweet-spot3,14,17,18,19. The energy levels of this system are shown schematically in Fig. 1b. The arrows indicate the transitions of interest; the blue and red arrows describe the transitions of qubit 1 and 2, respectively. Both pairs are degenerate in frequency, which is typical for transverse coupling. For simplicity, we label the states as if the qubits were uncoupled, although the single-qubit states are mixed by the coupling. This state mixing is central to the method we introduce here. As for all schemes with fixed coupling, the mixing can also lead to a difference between the operational basis and the readout basis. Solutions to this problem depend on the details of the readout scheme. For flux qubits, the readout naturally involves shifting the qubits to a bias position where the problem does not exist.

Figure 1: Coupled qubit system and transitions.
figure 1

a, Optical micrograph of the sample, showing two flux qubits coloured in blue and red. The inset shows part of each qubit loop, both containing four Josephson tunnel junctions. Overlapping the qubit loops, in light grey, are the qubit-state detectors based on superconducting quantum interference devices. In the top right and bottom left are the two antennas from which the qubits are driven. b, Energy-level diagram of the coupled qubit system. Arrows of the same colour indicate transitions of the same qubit and are degenerate in frequency. c, Pulse sequence used for the coherent excitation of the qubits. The first pulse is resonant with qubit 1. The second pulse, applied from both antennas simultaneously with independent amplitudes and phases, is resonant with qubit 2. After the second pulse the state of both qubits is read out. d, The normalized transition strengths of the four transitions in b as a function of the net driving amplitudes a1/(a1+a2) for ϕ2−ϕ1=0. For ϕ2−ϕ1=π the dashed and solid lines are interchanged. The black dotted lines indicate the locations of the darkened transitions.

Full size image

Our method aims at the selective excitation of a transition of one of the degenerate pairs and is based on simultaneously driving both qubits with the resonance frequency of that pair, employing different amplitudes and phases. The driving is described with the Hamiltonian

where ω is the driving frequency and ai and ϕi are the driving amplitude and phase for qubit i. The transition strength , with the driving Hamiltonian transformed to an appropriate rotating frame (see Supplementary Information), governs the transition rate and depends on both ai and ϕi. Figure 1d shows the normalized as a function of a1/(a1+a2), for a fixed phase difference ϕ2−ϕ1=0. Clearly the two transitions of each qubit generally do not have the same strength T, despite their frequency degeneracy. In addition, for certain settings individual transitions are completely suppressed: the transition is darkened (black dotted lines in Fig. 1d). The darkened transitions provide the desired conditions where one of the two transitions can be excited individually, even though the driving field is resonant with both transitions. The difference in transition strength can be understood intuitively. As coupling leads to mixing of the single-qubit eigenstates, qubit 2 can be excited by driving qubit 1 with a frequency that is resonant with qubit 2. This indirect driving can enhance, counteract and even cancel direct driving of qubit 2. The effect differs for the two degenerate transitions, because the states involved are different superpositions of the single-qubit eigenstates (see Supplementary Information). For J≪|Δ1−Δ2|, and assuming Δ1>Δ2, one readily finds the driving amplitude ratio

which yields for ϕ2−ϕ1=0 and for ϕ2−ϕ1=π. These are the transitions of qubit 2. For the transitions of qubit 1, that is and , the amplitude ratio is simply inverted. Expressions for arbitrary J are given in the Supplementary Information. Note that for a darkened transition in one qubit, the other is driven more strongly. This non-resonant driving of the other qubit limits the maximum operation frequency. From the usual condition that the transition strength of the unwanted transition should be smaller than its frequency detuning one can derive the maximum operation frequency 4J/h, which is as fast as any other two-qubit operation.

To experimentally demonstrate this method we employ two coupled flux qubits1, each consisting of a superconducting loop interrupted by four Josephson tunnel junctions. When biased with a magnetic flux close to half a flux quantum Φ0, the two states of each qubit are clockwise and anticlockwise persistent-current states. These currents Ip produce opposite magnetic fields, which provides the coupling for the two qubits. Two independent a.c.-operated superconducting quantum interference device magnetometers are used to simultaneously read out the states of the qubits20,21. These are switching-type detectors, where the switching probability Psw is a measure for the magnetic field. At a bias of Φ0/2 the system is described by the Hamiltonian of equation (1). Here the eigenstates of each qubit are symmetric and antisymmetric superpositions of the two persistent-current states, with level separation Δ. The device is shown in Fig. 1a. The qubits are characterized by the persistent currents Ip,1=355 nA and Ip,2=460 nA and the energy splittings Δ1/h=7.88 GHz and Δ2/h=4.89 GHz. The qubit–qubit coupling strength is 2J/h=410 MHz.

For our fabricated quantum objects the spatial locations are well defined, and the individual control of amplitude and phase for each qubit according to equation (2) can be easily achieved using local magnetic fields. We employ two on-chip antennas, indicated as A1 and A2 in Fig. 1a, both coupling to both qubits, with a stronger coupling to the closer one. Driving the two qubits from both antennas is described with

where Aj and φj are the driving amplitude and phase for antenna j and mj i is the coupling of antenna j to qubit i. Note that any combination of ai and ϕi in equation (2) can be achieved with the proper choice of Aj and φj. For this device m12/m11=0.32, m21/m22=0.33 and m11=m22.

For the experimental demonstration we choose to focus on the degenerate transitions of qubit 2. We first show that, if the qubits are driven from a single antenna, the two degenerate transitions exhibit a different Rabi frequency. We apply two pulses on antenna 1: the first pulse is resonant with qubit 1; the second pulse is resonant with qubit 2. Figure 1c shows a schematic of the pulse sequence; note that here A2=0. The experiment is repeated for varying durations τ1 and τ2 of pulses 1 and 2. The switching probability Psw,1 of detector 1 is depicted in Fig. 2a, showing a few Rabi oscillation periods as a function of the pulse duration τ1. Varying τ2 does not lead to oscillations of qubit 1, as pulse 2 is non-resonant, and only relaxation is observed. The oscillations of qubit 2, induced by the second pulse, are visible in Psw,2 (Fig. 2b). Here we distinguish two oscillation frequencies. Along the white solid line, where qubit 1 is prepared in the excited state, qubit 2 oscillates with a Rabi frequency of 85 MHz. For qubit 1 prepared in the ground state, along the white dashed line, the Rabi frequency f=31 MHz of qubit 2 is lower. For qubit 1 in a superposition of the ground and excited states, qubit 2 shows a beating pattern of both oscillations.

Figure 2: Driving from a single antenna.
figure 2

Measurement of the state of the qubits, represented by switching probabilities Psw,1 and Psw,2, after applying a pulse of duration τ1 resonant with qubit 1, followed by a pulse of duration τ2 resonant with qubit 2. a, Psw,1, showing coherent oscillations of qubit 1 induced by pulse 1. The white solid and dashed lines indicate a π- and 2π-rotation respectively. For pulse 2, qubit 1 shows only relaxation. b, Psw,2, showing coherent oscillations induced by pulse 2. After an odd number of π-rotations on qubit 1, the oscillation frequency is higher than after an even number of π-rotations. For superposition states of qubit 1, a beating pattern of the two oscillations is observed. c–f, Level occupations Q of the four different levels. Note that a value of 0.2 has been added to Q11 to improve visibility.

Full size image

A more detailed analysis allows us to unravel the two frequencies of Fig. 2b and determine which levels are participating in each of the oscillations. We extract the level occupations Q00,Q01,Q10 and Q11 from the individual switching probabilities (see Supplementary Information). The result is shown in Fig. 2c–f. After an odd number of π-rotations of qubit 1, there are oscillations only between states 10 and 11, not for states 00 and 01. After an even number of π-rotations of qubit 1 the situation is reversed; now the states 00 and 01 oscillate. The two oscillation frequencies are clearly linked to the two different transitions.

To demonstrate the tunability of the transition strengths we drive both antennas simultaneously, using the same frequency and controlling independently the amplitudes A1,A2 and phases φ1,φ2. In this two-pulse experiment (Fig. 1c), the first pulse prepares qubit 1 with a π/2-rotation and the duration τ2 of the second pulse is varied. As qubit 1 is in a superposition state, both Rabi frequencies are present in the dynamics of qubit 2. In Fig. 3a–c we show the Fourier transform for the measured oscillations. Each graph is measured with a different amplitude ratio A1/A2, with fixed phase φ1=0 and varying φ2. Figure 3a, with A1/A2=1.3, shows a typical result for an arbitrary amplitude ratio; the Rabi oscillation frequencies of both transitions clearly depend on φ2−φ1, but nowhere is a transition darkened. Note the occurrence of equal Rabi frequencies for two phase conditions, as denoted by Y. For A1/A2=2.5 in Fig. 3b we observe that for φ2−φ1≈π (indicated by X0) the transition is fully darkened, whereas the transition shows a non-zero oscillation frequency. In Fig. 3c with A1/A2=6.3 the situation is reversed, with the transition being suppressed (denoted by X1). This clearly demonstrates our method, as we selectively excite one of two transitions, despite their frequency degeneracy. Calculations of T are in good agreement with the experimental results, provided we allow for different transmissions of amplitudes and phases of the antennas to the qubits, which we attribute to the influence of the detector circuits.

Figure 3: Transition-strength tuning and darkened transitions.
figure 3

a–c, Rabi frequency dependence on φ2−φ1 for three different amplitude ratios. The colour scale represents the Fourier component of Psw,2(τ2). Qubit 1 is prepared with a π/2-rotation. Markers X0 and X1 indicate the conditions for a darkened transition on and , respectively. d–f, Psw,2 versus the durations τ1 and τ2. The white solid and dashed lines indicate a π- and 2π-rotation of qubit 1, respectively. The driving conditions are as marked by Y left arrow (d), X0 (e) and X1 (f).

Full size image

To further investigate the special cases of equal Rabi frequencies (Y), and darkened transitions (X0, X1), we again vary the durations τ1 and τ2, using both antennas for the second pulse. The results should be compared with Fig. 2b. Figure 3d shows Psw,2 for driving conditions denoted by Y (left arrow): the oscillation frequency of qubit 2 does not depend on the state of qubit 1. For the conditions marked by X0, we observe oscillations of qubit 2 only when qubit 1 is in the ground state, as shown in Fig. 3e. Similarly for the conditions marked by X1, now we observe oscillations of qubit 2 only if qubit 1 is in the excited state (Fig. 3f).

The demonstrated capability to selectively manipulate transition strengths in frequency-degenerate transitions has important applications. A π-pulse using condition X1 or X0 provides a 1-controlled- and 0-controlled-NOT gate, respectively. This enables certain systems, including the flux qubit used here, to be fully operated at the coherence-optimal point, without level shifting by either d.c. or strong a.c. signals. Note that the use of extra coupling elements is neither required nor prohibited. If extra coupling elements are used, our method can replace more complicated schemes. For conditions similar to Y, taking care of the individual rotation angles, also single-qubit gates can be implemented. The controlled-NOT and single-qubit gates together form a universal set, implying that our method fulfils all requirements for constructing any single- or two-qubit gate. Up to small errors, the method also scales to three or more qubits with transverse coupling. Detailed calculations will be presented elsewhere.

We have introduced and experimentally demonstrated a method to control transition strengths by applying a non-uniform driving field. Darkened transitions are created and employed for the selective excitation of degenerate transitions. As this method improves the simplicity and coherence conditions for operations in a variety of quantum systems, the prospect of carrying out large-scale quantum algorithms is enhanced significantly.