Abstract
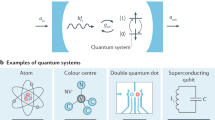
In circuit quantum electrodynamics1,2,3,4,5,6,7,8,9,10 (QED), where superconducting artificial atoms are coupled to on-chip cavities, the exploration of fundamental quantum physics in the strong-coupling regime has greatly evolved. In this regime, an atom and a cavity can exchange a photon frequently before coherence is lost. Nevertheless, all experiments so far are well described by the renowned Jaynes–Cummings model11. Here, we report on the first experimental realization of a circuit QED system operating in the ultrastrong-coupling limit12,13, where the atom–cavity coupling rate g reaches a considerable fraction of the cavity transition frequency ωr. Furthermore, we present direct evidence for the breakdown of the Jaynes–Cummings model. We reach remarkable normalized coupling rates g/ωr of up to 12% by enhancing the inductive coupling14 of a flux qubit to a transmission line resonator. Our circuit extends the toolbox of quantum optics on a chip towards exciting explorations of ultrastrong light–matter interaction.
Similar content being viewed by others
Main
At microwave frequencies, strong coupling is feasible because of the enormous design flexibility of superconducting circuit QED systems1,2. Here, small cavity-mode volumes and large dipole moments of artificial atoms15 enable coupling rates g of about16,17 1% of the cavity-mode frequency ωr. Nevertheless, as in other systems18,19,20,21,22, the quantum dynamics of these strongly coupled systems follows the Jaynes–Cummings model, which describes the coherent exchange of a single excitation between the atom and the cavity mode. Although the Hamiltonian of a realistic atom–cavity system contains so-called counter-rotating terms allowing the simultaneous creation or annihilation of an excitation in both, atom and cavity mode, these terms can be safely neglected for small normalized coupling rates g/ωr. However, when g becomes a significant fraction of ωr, the counter-rotating terms are expected to manifest, giving rise to exciting effects in QED. This ultrastrong-coupling regime is difficult to reach in quantum-optical cavity QED (refs 19, 20), but was recently realized in a solid-state semiconductor system23,24. There, quantitative deviations from the Jaynes–Cummings model have been observed, but direct experimental proof of its breakdown by means of an unambiguous feature is still missing.
In this work, we exploit the potential of flux-based superconducting quantum circuits to reach the ultrastrong-coupling regime13,14 and show direct evidence of physics beyond the Jaynes–Cummings model. To this end, we use the large nonlinear inductance of a Josephson junction shared between a flux qubit and a coplanar waveguide resonator. The transmission spectra of the combined system reveal qubit–mode couplings g/ωr of up to 12% and anticrossings that cannot be explained by the Jaynes–Cummings model. Instead, they are caused by the simultaneous creation (annihilation) of two excitations, one in the qubit and one in a resonator mode, while annihilating (creating) only one excitation in a different resonator mode. The size of the anticrossings illustrates the importance of the counter-rotating terms for the qubit–cavity dynamics in the ultrastrong-coupling limit.
Images of our quantum circuit and a schematic of the measurement set-up are shown in Fig. 1. At a current antinode for the λ-mode of a niobium superconducting resonator (Fig. 1a–c),a part of the centre conductor is replaced with a narrow aluminium strip interrupted by a large-area Josephson junction (see the Methods section for fabrication details). This junction mediates most of the inductive coupling between a superconducting flux qubit25 galvanically connected to the strip. The qubit consists of three nanometre-scaled Josephson junctions interrupting a superconducting loop, which is threaded by an external flux bias Φx. Scanning electron microscope (SEM) images of the qubit loop and the Josephson junctions are shown in Fig. 1d–f. For suitable junction sizes, the qubit potential landscape can be reduced to a double-well potential, where the two minima correspond to states with clockwise and anticlockwise persistent currents ±Ip. At δ Φx=Φx−Φ0/2=0, these two states are degenerate and separated by an energy gap Δ. In the qubit eigenbasis, the qubit Hamiltonian reads  . Here,
. Here,  is the qubit transition frequency, which can be adjusted by an external flux bias. We note, that for our flux qubit the two-level approximation is well justified because of its large anharmonicity. The resonator modes are described as harmonic oscillators,
is the qubit transition frequency, which can be adjusted by an external flux bias. We note, that for our flux qubit the two-level approximation is well justified because of its large anharmonicity. The resonator modes are described as harmonic oscillators,  , where ωn is the resonance frequency and n is the resonator-mode index. The operator
, where ωn is the resonance frequency and n is the resonator-mode index. The operator  (
( ) creates (annihilates) a photon in the nth resonator mode. Owing to the inhomogeneous transmission line geometry14 (see Fig. 1d), the higher mode frequencies of our resonator are not integer multiples of the fundamental resonance frequency ω1. Throughout this work, we refer to the nth mode as the n λ/2-mode. Then, the Hamiltonian of our quantum circuit can be written as
) creates (annihilates) a photon in the nth resonator mode. Owing to the inhomogeneous transmission line geometry14 (see Fig. 1d), the higher mode frequencies of our resonator are not integer multiples of the fundamental resonance frequency ω1. Throughout this work, we refer to the nth mode as the n λ/2-mode. Then, the Hamiltonian of our quantum circuit can be written as

Here,  denote Pauli operators, gn is the coupling rate of the qubit to the nth cavity mode and the flux dependence is encoded in sinθ=Δ/ℏωq and cosθ. The operator
denote Pauli operators, gn is the coupling rate of the qubit to the nth cavity mode and the flux dependence is encoded in sinθ=Δ/ℏωq and cosθ. The operator  is conveniently expressed as the sum of the qubit raising (
is conveniently expressed as the sum of the qubit raising ( ) and lowering (
) and lowering ( ) operator. Thus, in contrast to the Jaynes–Cummings model, the Hamiltonian in equation (1) explicitly contains counter-rotating terms of the form
) operator. Thus, in contrast to the Jaynes–Cummings model, the Hamiltonian in equation (1) explicitly contains counter-rotating terms of the form  and
and  . Figure 1g shows a schematic of our measurement set-up. The quantum circuit is located at the base temperature of 15 mK in a dilution refrigerator. We measure the amplified resonator transmission using a vector network analyser. For qubit spectroscopy measurements, the system is excited with a second microwave tone ωs with power Ps, while using the 3λ/2-mode at ω3/2π=7.777 GHz for dispersive readout9,26.
. Figure 1g shows a schematic of our measurement set-up. The quantum circuit is located at the base temperature of 15 mK in a dilution refrigerator. We measure the amplified resonator transmission using a vector network analyser. For qubit spectroscopy measurements, the system is excited with a second microwave tone ωs with power Ps, while using the 3λ/2-mode at ω3/2π=7.777 GHz for dispersive readout9,26.
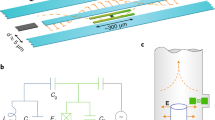
a, Optical image of the superconducting λ/2 coplanar waveguide resonator (light blue rectangle). Black rectangles: area shown in b. Red rectangle: area shown in d. b, SEM image of one of the coupling capacitors. c, Sketch of the current distribution of the first three resonator modes. Their resonance frequencies are ω1/2π=2.782 GHz (λ/2, red), ω2/2π=5.357 GHz (λ, blue) and ω3/2π=7.777 GHz (3λ/2, green). The cavity modes ωn are measured at maximum qubit–cavity detuning (Φx=0). In general, the flux dependence of ωn is very weak, except for the regions close to Φx=±Φ0/2. d, SEM image of the galvanically coupled flux qubit (see the Methods section for fabrication details). The width in the overlap regions with the centre conductor is 20 μm, and that of the constriction is 1 μm. Orange rectangle: area shown in e. Green rectangle: area shown in f. e, SEM image of the large Josephson junction. Its Josephson inductance LJ is responsible for approximately 85% of the qubit–resonator coupling. f, One Josephson junction of the qubit loop. The area of this junction is 14% of the one shown in e. g, Schematic of the measurement set-up. The transmission through the cavity at ωrf is measured using a vector network analyser (VNA). A second microwave signal at ωs is used for two-tone qubit spectroscopy. The input signal is attenuated at various temperature stages and coupled into the resonator (light blue) through the capacitors Cκ. The crossed squares represent Josephson junctions. A circulator isolates the sample from the amplifier noise.
We first present measurements allowing the extraction of the coupling constants of the qubit to the first three resonator modes. The spectroscopy data in Fig. 2a show the dressed qubit transition frequency1,26 with the expected hyperbolic flux dependence and a minimum at δ Φx=0. Furthermore, the two lowest resonator modes (ω1 and ω2) are visible. In principle, a fit to the Hamiltonian in equation (1) would yield all system parameters. However, our measurement resolution does not allow us to reliably determine the system parameters, in particular the undressed qubit energy gap Δ and the coupling constants gn in this situation. Instead, we extract them from a cavity transmission spectrum with negligible photon population. For that purpose, we first measure the power-dependent a.c.-Zeeman shift of the qubit transition frequency at δ Φx=0. The data are shown in the inset of Fig. 2a. The average photon number  can be estimated using the relation
can be estimated using the relation  (refs 6, 8), where κ3/2π≈3.7 MHz is the full-width at half-maximum of the cavity resonance and Prf is the probe power referred to the input of the resonator. Figure 2b shows a colour-coded transmission spectrum for the 3λ/2-mode as a function of δ Φx. The data are recorded at an input power Prf≈−140 dBm (green data point in Fig. 2a, inset) corresponding to
(refs 6, 8), where κ3/2π≈3.7 MHz is the full-width at half-maximum of the cavity resonance and Prf is the probe power referred to the input of the resonator. Figure 2b shows a colour-coded transmission spectrum for the 3λ/2-mode as a function of δ Φx. The data are recorded at an input power Prf≈−140 dBm (green data point in Fig. 2a, inset) corresponding to  .
.
a, Microwave spectroscopy of the coupled qubit–cavity system. The measured transmission magnitude (colour coded, blue: low; white: high) is plotted as a function of the relative flux bias δ Φx and the spectroscopy frequency ωs/2π. The black dashed lines indicate the dressed9,26 energy-level spectrum of Hamiltonian (1) obtained with the fit parameters from the cavity transmission data in Fig. 2c. Owing to the long acquisition time, we need to account for a small flux drift using a slightly smaller value for Ip. The spectrum is recorded at Prf corresponding to  . Near the anticrossing regions with the two lowest cavity modes, the transmitted signal through the readout mode ω3 disappears in the noise floor. Inset: Centre frequency of the qubit spectroscopy signal at δ Φx=0 as a function of the probe power Prf. The full-width at half-maximum of the qubit signal is approximately 80 MHz in the low-power limit Prf,Ps→0. Red line: fit to the linear region30. The green dot indicates the power level at which the spectra in b,c and Fig. 3 are recorded. b, Cavity transmission (3λ/2-mode, linear scale, arbitrary units) as a function of δ Φx and probe frequency ωrf/2π. c, The same spectrum as in b. Black lines: numerical fit of the spectrum of the Hamiltonian (1) to the data. d, Cavity transmission (λ-mode, linear scale, arbitrary units) as a function of δ Φx and probe frequency ωrf/2π. The spectrum is recorded at Prf corresponding to
. Near the anticrossing regions with the two lowest cavity modes, the transmitted signal through the readout mode ω3 disappears in the noise floor. Inset: Centre frequency of the qubit spectroscopy signal at δ Φx=0 as a function of the probe power Prf. The full-width at half-maximum of the qubit signal is approximately 80 MHz in the low-power limit Prf,Ps→0. Red line: fit to the linear region30. The green dot indicates the power level at which the spectra in b,c and Fig. 3 are recorded. b, Cavity transmission (3λ/2-mode, linear scale, arbitrary units) as a function of δ Φx and probe frequency ωrf/2π. c, The same spectrum as in b. Black lines: numerical fit of the spectrum of the Hamiltonian (1) to the data. d, Cavity transmission (λ-mode, linear scale, arbitrary units) as a function of δ Φx and probe frequency ωrf/2π. The spectrum is recorded at Prf corresponding to  because of a higher insertion loss of this cavity mode. Black lines: numerically evaluated energy-level spectrum with parameters from c.
because of a higher insertion loss of this cavity mode. Black lines: numerically evaluated energy-level spectrum with parameters from c.
We observe a spectrum with a large number of anticrossings resulting from the multimode structure of our cavity system. To extract the individual coupling constants gn, we compute the lowest nine transition frequencies of the Hamiltonian given in equation (1) incorporating the first three resonator modes. Fitting the results to the spectrum of the 3λ/2-mode shows excellent agreement with the measured data as shown in Fig. 2c. We note that the spectrum for the λ-mode shown in Fig. 2d can be well described without additional fitting using the parameters extracted from the 3λ/2-mode. For the qubit, we obtain 2Ip=630 nA and Δ/h=2.25 GHz. The latter deviates significantly from the dressed qubit transition frequency  at δ Φx=0 (see Fig. 2a, inset) because of the strong qubit–cavity interaction. Most importantly, we find coupling rates of g1/2π=314 MHz, g2/2π=636 MHz and g3/2π=568 MHz. The values for gn correspond to normalized coupling rates gn/ωn of remarkable 11.2%, 11.8% and 7.3%, respectively. These large coupling rates allow us to enter the ultrastrong-coupling regime and, as we will show below, lead to significant deviations from the Jaynes–Cummings physics.
at δ Φx=0 (see Fig. 2a, inset) because of the strong qubit–cavity interaction. Most importantly, we find coupling rates of g1/2π=314 MHz, g2/2π=636 MHz and g3/2π=568 MHz. The values for gn correspond to normalized coupling rates gn/ωn of remarkable 11.2%, 11.8% and 7.3%, respectively. These large coupling rates allow us to enter the ultrastrong-coupling regime and, as we will show below, lead to significant deviations from the Jaynes–Cummings physics.
In the following, we analyse the features in our data that constitute unambiguous evidence for the breakdown of the rotating-wave approximation inherent to the Jaynes–Cummings model. In Fig. 3, we compare the energy-level spectrum of the Hamiltonian in equation (1) with that of a three-mode Jaynes–Cummings model. We note that, depending on δ Φx, there are regions where our data can be well described by the Jaynes–Cummings model, and regions where there are significant deviations (see Fig. 3a). For our analysis we use the notation  , where q={g,e} denote the qubit ground or excited state, respectively, and |Nn〉={|0〉,|1〉,|2〉,…} represents the Fock state with photon occupation N in the nth resonator mode. At the outermost anticrossings (Fig. 3b), where ω3≈ωq, the eigenstates |ψ±〉 of the coupled system are in good approximation symmetric and antisymmetric superpositions of |e,0,0,0〉 and |g,0,0,1〉. This exchange of a single excitation between the qubit and the resonator is a characteristic of the Jaynes–Cummings model. On the contrary, the origin of the anticrossing shown in Fig. 3c is of a different nature: the dominant contributions to the eigenstates |ψ±〉 are approximate symmetric and antisymmetric superpositions of the degenerate states ϕ1=|e,1,0,0〉 and ϕ2=|g,0,0,1〉. The transition from ϕ1 to ϕ2 can be understood as the annihilation of two excitations, one in the λ/2-mode and one in the qubit, while, simultaneously, creating only one excitation in the 3λ/2-mode. Such a process can result only from counter-rotating terms as they are present in the Hamiltonian (1), but not within the Jaynes–Cummings approximation. Here, only eigenstates with an equal number of excitations can be coupled. Although counter-rotating terms in principle exist in any real circuit QED system, their effects become prominent only in the ultrastrong-coupling limit with large normalized couplings gn/ωn as realized in our system. Hence, the observed anticrossing shown in Fig. 3c is a direct experimental manifestation of physics beyond the rotating-wave approximation in the Jaynes–Cummings model. As shown in Fig. 3d, the latter would imply a crossing of the involved energy levels, which is not observed. A similar argument applies to the innermost anticrossings of the 3λ/2-mode (see Fig. 3a), although the involved eigenstates have a more complicated character, and to the innermost anticrossings of the λ-mode shown in Fig. 2d.
, where q={g,e} denote the qubit ground or excited state, respectively, and |Nn〉={|0〉,|1〉,|2〉,…} represents the Fock state with photon occupation N in the nth resonator mode. At the outermost anticrossings (Fig. 3b), where ω3≈ωq, the eigenstates |ψ±〉 of the coupled system are in good approximation symmetric and antisymmetric superpositions of |e,0,0,0〉 and |g,0,0,1〉. This exchange of a single excitation between the qubit and the resonator is a characteristic of the Jaynes–Cummings model. On the contrary, the origin of the anticrossing shown in Fig. 3c is of a different nature: the dominant contributions to the eigenstates |ψ±〉 are approximate symmetric and antisymmetric superpositions of the degenerate states ϕ1=|e,1,0,0〉 and ϕ2=|g,0,0,1〉. The transition from ϕ1 to ϕ2 can be understood as the annihilation of two excitations, one in the λ/2-mode and one in the qubit, while, simultaneously, creating only one excitation in the 3λ/2-mode. Such a process can result only from counter-rotating terms as they are present in the Hamiltonian (1), but not within the Jaynes–Cummings approximation. Here, only eigenstates with an equal number of excitations can be coupled. Although counter-rotating terms in principle exist in any real circuit QED system, their effects become prominent only in the ultrastrong-coupling limit with large normalized couplings gn/ωn as realized in our system. Hence, the observed anticrossing shown in Fig. 3c is a direct experimental manifestation of physics beyond the rotating-wave approximation in the Jaynes–Cummings model. As shown in Fig. 3d, the latter would imply a crossing of the involved energy levels, which is not observed. A similar argument applies to the innermost anticrossings of the 3λ/2-mode (see Fig. 3a), although the involved eigenstates have a more complicated character, and to the innermost anticrossings of the λ-mode shown in Fig. 2d.
a, Cavity transmission (3λ/2-mode, linear scale, arbitrary units) as a function of δ Φx and probe frequency ωrf/2π. Black dashed lines in all plots: energy-level spectrum obtained from the Hamiltonian (1). Coloured lines in all plots: energy-level spectrum obtained from the Jaynes–Cummings model (dark blue: |g,0,0,1〉, except for anticrossing region shown in b; green: |e,1,0,0〉; light blue: |e,0,1,0〉 and |e,2,0,0〉, which are indistinguishable within the resolution of this plot. Grey dashed rectangle: areas magnified in b–d. b, Single excitation anticrossing. The quantitative deviations of the Jaynes–Cummings model from equation (1) are attributed to a small admixture of the state |g,1,1,0〉. The uncoupled states are indicated by grey dashed lines. c, Avoided crossing resulting from a coupling between the degenerate states |g,0,0,1〉 and |e,1,0,0〉. This is caused by counter-rotating terms in the Hamiltonian (1). A detailed analysis yields a minor admixture of |g,1,1,0〉 (superposition states:  )). This admixture has no effect on the reasoning presented in the main text. The energy-level spectrum obtained from the Jaynes–Cummings model is omitted for clarity. The dominant contributions to the superposition states of the innermost anticrossings in Fig. 2d are |g,0,1,0〉,|g,2,0,0〉a n d|e,1,0,0〉. d, The same as in c, but for the Jaynes–Cummings model. Within numerical accuracy, no anticrossing is predicted, clearly contradicting the data.
)). This admixture has no effect on the reasoning presented in the main text. The energy-level spectrum obtained from the Jaynes–Cummings model is omitted for clarity. The dominant contributions to the superposition states of the innermost anticrossings in Fig. 2d are |g,0,1,0〉,|g,2,0,0〉a n d|e,1,0,0〉. d, The same as in c, but for the Jaynes–Cummings model. Within numerical accuracy, no anticrossing is predicted, clearly contradicting the data.
We have presented measurements on a superconducting circuit QED system in the ultrastrong-coupling regime. Our transmission spectra are in excellent agreement with theoretical predictions and show clear evidence for physics beyond the Jaynes–Cummings model. This system can act as an on-chip prototype for unveiling the physics of ultrastrong light–matter interaction. Future explorations may include squeezing, causality effects in quantum field theory27, the generation of bound states of qubits and photons28, in situ switching of distinct physical regimes29 and ultrafast quantum operations in circuit QED for quantum information protocols.
Methods
Fabrication details.
The coplanar waveguide resonator is fabricated using optical lithography and reactive ion etching. We use a thermally oxidized (50 nm) silicon substrate with a 100-nm-thick niobium film, deposited by d.c.-magnetron sputtering before patterning. The coplanar waveguide centre conductor is 20 μm wide and separated from the lateral ground planes by a gap of 12 μm, resulting in a characteristic impedance of approximately 50 Ω. The resonator with a length of 23 mm is defined by two interdigital coupling capacitors (see Fig. 1b) with a numerically calculated capacitance of about 10 fF. The centre conductor is interrupted by a gap of 80 μm at a maximum of the current distribution for the λ-mode (see Fig. 1c). At this point, the amplitude of the standing current wave for the λ/2- and 3λ/2-mode is smaller by a factor of  . The aluminium strip connected to the flux qubit and the large Josephson junction is fabricated by electron-beam lithography and Al/AlOx/Al shadow evaporation techniques. For the bottom and top aluminium layer, we use a thickness of 50 and 80 nm, respectively. For the in situ oxidation of the bottom layer, pure oxygen (=2×10−4 mbar; 22 min) is used. Two of the qubit Josephson junctions have an area A≈250×140 nm2 whereas the other junction is smaller by a factor of α≈0.7. The critical current density of the Josephson junctions is jc≈1.3 kA cm−2, leading to a Josephson energy of EJ≈224 GHz for a junction with area A. The area of the qubit loop is roughly 20×9 μm2 and the large Josephson junction mediating the ultrastrong qubit–cavity coupling has an area of about 7A.
. The aluminium strip connected to the flux qubit and the large Josephson junction is fabricated by electron-beam lithography and Al/AlOx/Al shadow evaporation techniques. For the bottom and top aluminium layer, we use a thickness of 50 and 80 nm, respectively. For the in situ oxidation of the bottom layer, pure oxygen (=2×10−4 mbar; 22 min) is used. Two of the qubit Josephson junctions have an area A≈250×140 nm2 whereas the other junction is smaller by a factor of α≈0.7. The critical current density of the Josephson junctions is jc≈1.3 kA cm−2, leading to a Josephson energy of EJ≈224 GHz for a junction with area A. The area of the qubit loop is roughly 20×9 μm2 and the large Josephson junction mediating the ultrastrong qubit–cavity coupling has an area of about 7A.
Theoretical description of the coupling.
The qubit–cavity coupling is determined by the local inductance M=LJ+L. Here, LJ is the Josephson inductance of the coupling junction and L is the inductance of the shared edge between the centre conductor and the qubit. Although LJ>L dominates M, it has negligible influence on the vacuum current  in the resonator because the total resonator inductance Lr≫LJ,L. Consequently, the coupling strengths can be written as ℏgn=M InIp. This result can also be obtained analytically from a more thorough theoretical treatment14. From the experimental values of gn, we obtain LJ≈60 pH in agreement with our junction parameters.
in the resonator because the total resonator inductance Lr≫LJ,L. Consequently, the coupling strengths can be written as ℏgn=M InIp. This result can also be obtained analytically from a more thorough theoretical treatment14. From the experimental values of gn, we obtain LJ≈60 pH in agreement with our junction parameters.
References
Blais, A., Huang, R-S., Wallraff, A., Girvin, S. M. & Schoelkopf, R. J. Cavity quantum electrodynamics for superconducting electrical circuits: An architecture for quantum computation. Phys. Rev. A 69, 062320 (2004).
Wallraff, A. et al. Strong coupling of a single photon to a superconducting qubit using circuit quantum electrodynamics. Nature 431, 162–167 (2004).
Chiorescu, I. et al. Coherent dynamics of a flux qubit coupled to a harmonic oscillator. Nature 431, 159–162 (2004).
Johansson, J. et al. Vacuum Rabi oscillations in a macroscopic superconducting qubit LC oscillator system. Phys. Rev. Lett. 96, 127006 (2006).
Schuster, D. I. et al. Resolving photon number states in a superconducting circuit. Nature 445, 515–518 (2007).
Astafiev, O. et al. Single artificial-atom lasing. Nature 449, 588–590 (2007).
Deppe, F. et al. Two-photon probe of the Jaynes–Cummings model and controlled symmetry breaking in circuit QED. Nature Phys. 4, 686–691 (2008).
Fink, J. et al. Climbing the Jaynes–Cummings ladder and observing its nonlinearity in a cavity QED system. Nature 454, 315–318 (2008).
Abdumalikov, A., Astafiev, O., Nakamura, Y., Pashkin, Y. & Tsai, J. Vacuum Rabi splitting due to strong coupling of a flux qubit and a coplanar-waveguide resonator. Phys. Rev. B 78, 180502 (2008).
Hofheinz, M. et al. Synthesizing arbitrary quantum states in a superconducting resonator. Nature 459, 546–549 (2009).
Jaynes, E. T. & Cummings, F. W. Comparison of quantum and semiclassical radiation theories with application to the beam maser. Proc. IEEE 51, 89–109 (1963).
Ciuti, C. & Carusotto, I. Input–output theory of cavities in the ultrastrong coupling regime: The case of time-independent cavity parameters. Phys. Rev. A 74, 033811 (2006).
Devoret, M., Girvin, S. & Schoelkopf, R. Circuit-QED: How strong can the coupling between a Josephson junction atom and a transmission line resonator be? Ann. Phys. 16, 767–779 (2007).
Bourassa, J. et al. Ultrastrong coupling regime of cavity QED with phase-biased flux qubits. Phys. Rev. A 80, 032109 (2009).
Niemczyk, T. et al. Fabrication technology of and symmetry breaking in superconducting quantum circuits. Supercond. Sci. Technol. 22, 034009 (2009).
Schoelkopf, R. J. & Girvin, S. M. Wiring up quantum systems. Nature 451, 664–669 (2008).
Bishop, L. et al. Nonlinear response of the vacuum Rabi resonance. Nature Phys. 5, 105–109 (2008).
Thompson, R. J., Rempe, G. & Kimble, H. J. Observation of normal-mode splitting for an atom in an optical cavity. Phys. Rev. Lett. 68, 1132–1135 (1992).
Walther, H., Varcoe, B. T. H., Englert, B-G. & Becker, T. Cavity quantum electrodynamics. Rep. Prog. Phys. 69, 1325–1382 (2006).
Haroche, S. & Raimond, J-M. Exploring the Quantum (Oxford Univ. Press, 2006).
Reithmaier, J. P. et al. Strong coupling in a single quantum dot semiconductor microcavity system. Nature 432, 197–200 (2004).
Gröblacher, S., Hammerer, K., Vanner, M. R. & Aspelmeyer, M. Observation of strong coupling between a micromechanical resonator and an optical cavity field. Nature 460, 724–727 (2009).
Günter, G. et al. Sub-cycle switch-on of ultrastrong light–matter interaction. Nature 458, 178–181 (2009).
Anappara, A. et al. Signatures of the ultrastrong light–matter coupling regime. Phys. Rev. B 79, 201303 (2009).
Mooij, J. E. et al. Josephson persistent-current qubit. Science 285, 1036–1039 (1999).
Schuster, D. I. et al. Ac stark shift and dephasing of a superconducting qubit strongly coupled to a cavity field. Phys. Rev. Lett. 94, 123602 (2005).
Sabin, C., Garcia-Ripoll, J. J., Solano, E. & Leon, J. Dynamics of entanglement via propagating microwave photons. Phys. Rev. B 81, 184501 (2010).
Hines, A. P., Dawson, C. M., McKenzie, R. H. & Milburn, G. J. Entanglement and bifurcations in Jahn-Teller models. Phys. Rev. A 70, 022303 (2004).
Peropadre, B., Forn-Diaz, P., Solano, E. & Garcia-Ripoll, J. J. Switchable ultrastrong coupling in circuit QED. Phys. Rev. Lett. 105, 023601 (2010).
Zueco, D., Reuther, G. M., Kohler, S. & Hanggi, P. Qubit-oscillator dynamics in the dispersive regime: Analytical theory beyond the rotating-wave approximation. Phys. Rev. A 80, 033846 (2009).
Acknowledgements
We thank G. M. Reuther for discussions and T. Brenninger, C. Probst and K. Uhlig for technical support. We acknowledge financial support by the Deutsche Forschungsgemeinschaft through SFB 631 and the German Excellence Initiative through NIM. E.S. acknowledges financial support from UPV/EHU Grant GIU07/40, Ministerio de Ciencia e Innovación FIS2009-12773-C02-01, Basque Government Grant IT472-10, European Projects EuroSQIP and SOLID. D.Z. acknowledges financial support from FIS2008-01240 and FIS2009-13364-C02-0 (MICINN).
Author information
Authors and Affiliations
Contributions
T.N. fabricated the sample, conducted the experiment and analysed the data presented in this work. F.D. provided important contributions regarding the interpretation of the results. T.N. and F.D. co-wrote the manuscript. J.J.G-R. provided the basic idea and the techniques for the numerical analysis of the data. E.S. and J.J.G-R. supervised the interpretation of the data. D.Z. and T.H. contributed to the understanding of the results and developed an analytical model of our system. H.H. contributed to the numerical analysis and helped with the experiment. E.P.M. contributed strongly to the experimental set-up. M.J.S. and F.H. contributed to discussions and helped edit the manuscript. A.M. and R.G. supervised the experimental part of the work.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
About this article
Cite this article
Niemczyk, T., Deppe, F., Huebl, H. et al. Circuit quantum electrodynamics in the ultrastrong-coupling regime. Nature Phys 6, 772–776 (2010). https://doi.org/10.1038/nphys1730
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys1730
This article is cited by
-
Sudden change of the photon output field marks phase transitions in the quantum Rabi model
Communications Physics (2024)
-
Ultrastrong to nearly deep-strong magnon-magnon coupling with a high degree of freedom in synthetic antiferromagnets
Nature Communications (2024)
-
Preparation of maximally-entangled states with multiple cat-state qutrits in circuit QED
Frontiers of Physics (2024)
-
On the two-photon quantum Rabi model at the critical coupling strength
Optical and Quantum Electronics (2024)
-
Generation of a hybrid W entangled state of three photonic qubits with different encodings
Quantum Information Processing (2024)