Main

Ruderman–Kittel–Kasuya–Yosida (RKKY) interaction is ubiquitous in solid-state systems containing diluted magnetic moments in a conducting non-magnetic host. It becomes dominant whenever there is a sufficiently strong exchange coupling between the localized moments and the conduction electrons. Then, the spins of the conduction electrons, which are on average unpolarized, are forced into a preferred direction in the vicinity of each moment. This preferential direction oscillates with increasing distance from the moment. A second localized moment will interact with this spin-density oscillation and perceive either a ferromagnetic or an antiferromagnetic coupling to the first, depending on their distance. Therefore, RKKY interaction is also called indirect magnetic exchange. The first indications of indirect magnetic exchange through conduction electrons came with the research on diluted bulk alloys, where a dependence of the interaction strength on the distance between the moments with an oscillation period of half the Fermi wavelength was proposed in an isotropic and continuous model1,2,3.

Direct experimental evidence for RKKY-like coupling of magnetic layers through transition-metal layers was obtained by spatial-averaging techniques9,10,11,12. There have been theoretical13,14,15 and experimental16 hints that accurate RKKY models have to take into account the topology of the Fermi surface and the discrete distribution of magnetic moments on the atomic lattice, but a direct experimental proof was hampered by the spatial averaging, which provides only fragmentary information on the distribution. However, as magnetic devices are becoming smaller and approaching the limit of nanostructures built by separate atoms, knowledge of the RKKY interaction on the atomic scale is essential.

By using scanning tunnelling spectroscopy, it became possible to investigate magnetic interactions in atom pairs17,18,19, but RKKY coupling was still detected only indirectly through the Kondo effect20. A direct detection of interactions is feasible with the recently developed technique of measuring magnetization curves of individual atoms using spin-polarized scanning tunnelling spectroscopy 21. Here, we study the indirect exchange interaction in well-defined pairs of magnetic adatoms with different orientations and distances both experimentally, by measuring single-atom magnetization curves, and by first-principles calculations, using the fully relativistic Korringa–Kohn–Rostoker Green function (KKR) method22,23. Our results show that an exact knowledge of the RKKY interaction on the atomic scale can be essential even for systems showing a rather simple Fermi surface.

We study the model system of cobalt adatoms on platinum(111) whose magnetic moment is forced to point perpendicular to the sample surface at the measurement temperature of T=0.3 K owing to a strong out-of-plane anisotropy of K≈9.3 meV (ref. 24). The adatom together with the neighbouring Pt atoms forms a large effective magnetic moment of on average m=3.5 μB (ref. 21). Examples of isolated adatom pairs with decreasing separations between two and five lattice constants are shown in Fig. 1a–e. Their lattice sites given in Fig. 1k–o can be extracted without ambiguity and we focus on face-centred-cubic adatoms (see Supplementary Information). Using Cr-coated probe tips sensitive to the out-of-plane magnetization, we measure the spin-resolved differential conductivity dI/dV of both adatoms to access their out-of-plane components of the time-averaged magnetization 〈Miz〉 in each pair as a function of the applied external magnetic field B (single-atom magnetization curves; see Methods and Supplementary Fig. S1). The corresponding curves are shown in Fig. 1f–j. In the following, their shape will be interpreted in terms of the magnetic interactions between the Co adatoms.

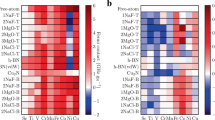
Figure 1: Magnetization curves of Co pairs.
figure 1

a–e, Topographs (2.1 nm×2.1 nm) of Co pairs with decreasing distance as indicated (vertical scale from 0 to 0.15 nm). f–j, Single-atom magnetization curves measured on the left atom (black dots) and on the right atom (blue dots) of each pair. The curves are vertically normalized to the saturation magnetization and horizontally offset to compensate for the effective tip field BT (ref. 21). The straight lines are calculated from the Ising model assuming magnetic moments m given in each panel. k–o, Ball models of the atomic configuration in the pairs and J resulting from the Ising model fit. The same colour indicates ferromagnetic coupling, different colours indicate antiferromagnetic coupling. (Tunnelling parameters: stabilization current Istab=0.8 nA, stabilization voltage Vstab=0.3 V, modulation voltage Vmod=20 mV (rms).)

Full size image

The two atoms in the pair with the largest separation of 1.21 nm (Fig. 1a) have typical S-shaped magnetization curves shown in Fig. 1f similar to the ones measured on isolated adatoms21. The magnetization of these two atoms is thus aligned parallel. When the separation in the pair is decreased by about one lattice constant (Fig. 1b), the corresponding magnetization curves are drastically changed (Fig. 1g) and a plateau appears around Bz=0 T. Obviously, the two magnetic moments of the pair couple to zero. Only when Bz exceeds a critical value |Bcritz|≈0.25 T does the antiparallel coupling break and the magnetizations of both adatoms saturate parallel to B. For another pair with identical distance but with a different neighbourhood of surrounding adatoms and defects (Fig. 1c), the right atom shows paramagnetic behaviour whereas the left atom behaves diamagnetically at low magnetic fields (Fig. 1h). Accordingly, its magnetization is again aligned antiparallel to that of the right atom and thus turns opposite to B. The coupling again breaks for |Bcritz|≥0.48 T. The same behaviour is found for the pair with a slightly lower separation (Fig. 1d,i), but now with significantly larger |Bcritz|≈1.25 T. When the interatomic distance is still smaller (Fig. 1e,j), the magnetization curves again look similar to those of isolated adatoms, indicating parallel alignment of the two spins.

Obviously, atoms 1 and 2 in the pair are subject to an oscillatory coupling energy J12, which forces their magnetizations to be aligned parallel (ferromagnetic coupling, J12>0) for pairs a, e and antiparallel (antiferromagnetic coupling, J12<0) for pairs b, c, d. However, for some pairs an additional effect breaks their symmetry, resulting in the asymmetric shape of the two magnetization curves. The symmetry breaking can be explained by a difference in the effective magnetic moments m1 and m2 of the two adatoms, which vary by ±2 μB around 3.5 μB owing to an inhomogeneous indirect-exchange mean field and to electronic inhomogeneity of the substrate21 (see Supplementary Discussion S2 and Figs S2,S3).

To theoretically describe the experimental magnetization curves, we use the following Hamiltonian:

where i (j) numbers the adatoms, Si=Mi/mi are normalized magnetic moments and mi are their absolute values (in μB). K is the anisotropy per atom. The first sum describes the distance-dependent exchange interactions. The second sum describes a uniaxial anisotropy favouring an out-of-plane (z) orientation of magnetization for positive K, and the third sum is the Zeeman energy. We apply two different models: (1) an Ising limit (Si=±1· ez, with ez being the unit vector along z) and (2) a quasiclassical Heisenberg limit. The expectation values of the atom magnetizations 〈Miz〉 have been calculated exactly and in case (2) additionally by Monte Carlo simulations assuming a temperature of T=0.3 K and an anisotropy of K=9.3 meV (see Methods). We vary m1, m2 and J12 to fit the measured magnetization curves. We find that the two different models are undistinguishable within the experimental error because of the large anisotropy, which forces the magnetization to point out of plane. Therefore, the results from the most instructive Ising model are shown. The fitted curves and the corresponding m and J values are given in Fig. 1f–o, demonstrating an excellent reproduction of the measured data. Obviously, for antiferromagnetic interaction between two atoms with magnetic moments m1 and m2 (m1≤m2, without loss of generality), the coupling can be broken if the external magnetic field becomes larger than |Bcritz|=−J12/m1. Assuming m1=3.5 μB, this simple formula results in an antiferromagnetic interaction of J≈−100 μeV for pairs b, c and J≈−250 μeV for pair d, which is already close to the results from the fits in Fig. 1. We carried out fits for about ten pairs with different distances d placed at different locations on the bare Pt(111) substrate. The resulting interaction energies J(d) are shown in Fig. 2a together with the relative position of the two atoms on the lattice in Fig. 2c. The J values from adatom triplets are also included (see below). Measurements of the local electronic density of states reveal that the atoms in pairs with a separation of larger than one lattice constant are sufficiently separated to exclude a strong overlapping of the electronic orbitals (Supplementary Fig. S5). Thus, there is no direct exchange interaction. Furthermore, dipolar interaction is at least three times smaller than the measurement temperature. Consequently, the extracted J values are dominated by RKKY interaction.

Figure 2: Distance dependence and directionality of RKKY interaction.
figure 2

a,b, Measured Jexp and calculated Jcalc in Co pairs (circles) and triplets (triangles, triangular triplet; crosses, straight triplet) as a function of distance d. The data points are coloured corresponding to the lattice positions of the adatoms in the pairs shown in c (first atom, black ball with spin up; second atom, coloured ball with spin direction as indicated by the arrow). Values in a are extracted from the magnetization curves by fitting to the Ising model. The error bars are calculated from the uncertainty in the magnetic moments (see Methods). The dotted line is a fit to the data of the pairs oriented along using a two-dimensional isotropic and continuous RKKY model. d, Plot of the calculated J values of b as a function of position in the (111) plane. Each hexagon corresponds to the lattice site of the second atom in a specific pair with the first atom fixed in the centre. The height and colour of each hexagon correspond to the size of J. e, The same as d, but with J values from the two-dimensional isotropic RKKY model evaluated on the discrete lattice.

Full size image

Note that the orientation of the pairs relative to the underlying Pt(111) lattice changes when the distance in the pairs is increased. Our measurements show that the RKKY interaction is ferromagnetic for small distances, becomes maximally antiferromagnetic for a distance of three lattice spacings in the direction (J≈−250 μeV) and then shows a damped oscillation between ferromagnetic and antiferromagnetic coupling. However, there is no well-defined wavelength. The data of the pairs along the close-packed direction () may be fitted to a two-dimensional isotropic and continuous RKKY model J(d)∝cos(2kFd)/(2kFd)2 using a Fermi wavelength λF=2π/kF=2±0.5 nm (Fig. 2a). However, for slightly different orientations, the isotropic model fails, and a strongly different wavelength has to be assumed (cyan-coloured, yellow and red data points). This proves a strong directionality of the RKKY interaction on the atomic scale. We propose that an upward-dispersing surface resonance crossing the Fermi energy at λF≈1.6 nm with an effective mass of about 1.5 me could be mediating the observed RKKY interaction25.

To explore the directionality further, we calculated the interaction energy J of adatom pairs using density functional theory in connection with the KKR method (see Methods). The calculated J(d) (Fig. 2b) reveals the same direction dependence as the measured data with a maximum in the antiferromagnetic coupling for a distance of three lattice spacings in the direction. The values are about three times larger than the experimental ones. Given the small absolute values of J of only several tens of a microelectronvolt, the correspondence is remarkably good. Figure 2d shows a different view of the calculated J values in a three-dimensional plot, which highlights the strong anisotropy of the RKKY interaction at the surface when being compared with a similar plot of the two-dimensional isotropic RKKY model in Fig. 2e. The strongest variation of J with increasing interatomic distance is observed along , whereas it is weaker along .

To demonstrate that the pairwise indirect exchange J(d) from Fig. 2 enables us to predict the behaviour of nanostructures built from a larger number of adatoms, we investigated triplets shown in Fig. 3. Figure 3a represents a triplet with an almost equidistant triangular shape with atom positions shown in Fig. 3c. From the map of the pairwise interaction in Fig. 2a,b, we expect a weak ferromagnetic coupling between the black and the red and between the green and the red adatoms, and a strong antiferromagnetic coupling between the black and the green adatoms. The measured magnetization curves are shown in Fig. 3e–g together with the calculated magnetization curves from the Ising model (equation (1)). Note that the experimental curves are very noisy around zero magnetic field, indicating that the moments are magnetically frustrated and switch between different almost degenerate ground states. The fitted J values in Fig. 3c in fact show that the energy difference between the two configurations (Sblackz,Sgreenz,Sredz)=(↑↓↑) and (↑↓↓) is only 20 μeV, which is lower than the thermal energy.

Figure 3: Magnetization curves of Co triplets.
figure 3

a,b, Topographs (2.8 nm×2.8 nm) of Co triplets with triangular (a) and straight (b) shape (vertical scale from 0 to 0.15 nm). c,d, Ball models and relative distances of the atom configuration in the triplets. e–j, Single-atom magnetization curves (dots with colours corresponding to c,d) measured on the three atoms in the triangular triplet (e–g) and straight triplet (h–j). The straight lines are calculated from the Ising model assuming mi=3.5 μB and Ji j as indicated in c,d. (Tunnelling parameters: Istab=0.8 nA, Vstab=0.3 V, Vmod=20 mV (rms).)

Full size image

The fitted J values are also included in Fig. 2a. Indeed, the J values deduced from the triplet are consistent with the values from the according pairs. The same comparison can be made for a triplet with an almost straight shape shown in Fig. 3b. The calculated J values from the KKR method for these two triplet geometries are included in Fig. 2b, also showing that the deviation from the pair interactions is negligible, that is, Ji jtriplet≃Ji jpair. Figure 2 thus enables us to precisely predict the magnetic state for larger adatom nanostructures coupled by indirect exchange simply by superposition of pairwise interactions.

As the RKKY interaction is mediated by the conduction electrons, which reside at the Fermi surface of the material, anisotropies of the Fermi surface could naturally explain the observed directionality. Indeed, even the shape of the rather simple Fermi surface of copper strongly modifies the electron motion as demonstrated recently26. In platinum, moreover, on top of the Fermi-surface hot spots there exists a Stoner enhancement for the investigated adatom-pair distances, which further modifies the interaction. This result will be important for the design of new nanostructures exploiting the indirect exchange in other materials, which usually have even more complex Fermi surfaces.

Using the obtained map of the pairwise exchange-coupling constants together with the technique of tip-induced adatom manipulation, it will be possible to design and build artificial adatom assemblies with interesting functionalities. For example, chains of coupled adatoms, which communicate the spin state through RKKY interaction, can serve to build elements for spin-logic circuits carrying out conventional binary computation using only the spin degree of freedom27. Finally, we anticipate that the demonstrated methods for extracting the interactions between individual magnetic atoms can be applied to other systems where a detailed knowledge of the indirect exchange is still lacking.

Methods

All measurements were made with an ultrahigh-vacuum system operated at T=0.3 K (ref. 28). Details of the measurement procedures, sample preparation and tip material can be found in ref. 21 (see also Supplementary Information). For Monte Carlo simulation of the magnetization curves in the quasiclassical Heisenberg model the Metropolis single-flip algorithm has been used. Up to 107 Monte Carlo steps have been carried out for each value of the out-of-plane component Bz of B after the system has reached thermal equilibrium. An additional averaging over several identical systems has been carried out.

The error in the experimental J, which is obtained from the fit of the measured magnetization curves to the model (equation (1)), is given by the uncertainty in the magnetic moments. They can vary by ±2 μB around the average value of 3.5 μB (ref. 21). The resulting error in J is ±60% in the antiferromagnetic case. J cannot be determined exactly for the ferromagnetic pairs (Supplementary Discussions S2,S3 and Figs S2–S4).

For the ab initio calculations we use the KKR method within the local-spin-density approximation (see Supplementary Methods). We implemented the solver of full-Dirac equations, available in the Jülich–Munich program23, in the real-space version of the program22. As the sizes of cobalt and platinum atoms are extremely different the deposited adatoms sink towards the substrate by about 20% of the surface interlayer distance. The total magnetic moment of a single cobalt atom with its four neighbouring platinum shells reaches a value of m=3.53 μB, in which the spin(orbital) contribution is about 3.05 μB(0.48 μB). The pairwise magnetic exchange interactions have been extracted by mapping the ab initio calculations to the quasiclassical Heisenberg model (equation (1)) and considering two magnetic configurations: a ferromagnetic solution with energy E↑↑ where both magnetic moments are parallel (perpendicular to the surface) and an antiferromagnetic solution with E↑↓, where the magnetic moments are antiparallel to each other. Ji j is then given by (E↑↓−E↑↑)/2.

Although it is well known that strong spin–orbit coupling, which is present on Pt(111), might lead to a significant Dzyaloshinskii–Moriya type of exchange Di j·(Si×Sj) resulting in a canting of the two spins in the pair29, we ignore it in the present analysis. Our KKR calculations show that the components of Di j are at most of the same strength as Ji j. However, even then, because of the large K, the resulting canting angle is small (6∘) and will not affect the measured magnetization curves considerably.